Для преодоления неприятности различных диапазонов значений частных параметров употребляются разного вида нормирования. Возможно продемонстрировать, что самый целесообразно осуществлять нормирование частных параметров их средними значениями:
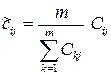 , .
, .
Нормированные значения всех частных параметров оказываются локализованными около единицы, что сглаживает их влияние на итог вычисления интегрального критерия, формула которого получает вид:
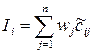 , .
, .
Для разглядываемого примера множество Парето с нормализованными значениями частных параметров представлено в таблице 13.
7 Решение проблемы разнонаправленности
частных параметров
Разглядывая линейную форму с частными параметрами, среди них и с нормированными, несложно подметить, что частные критерии с различным смыслом должны учитываться по-различному. Вправду, для одних частных параметров нужно как возможно большее значение (о таких параметрах говорят, что они имеют повышающее влияние на уровень качества варианта), для других нужно как возможно меньшее значение (о таких параметрах говорят, что они имеют понижающее влияние на уровень качества варианта).
Учесть данный факт возможно так: в линейной форме интегрального критерия значения частных параметров, повышающих уровень качества варианта, берутся со знаком плюс, а значения частных параметров, понижающих уровень качества, берутся со знаком минус. Наряду с этим формула вычисления частного критерия принимает вид:
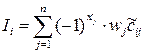 , ,
, ,
где – показатель направления влияния частного критерия на уровень качества варианта, вычисляемый по формуле:
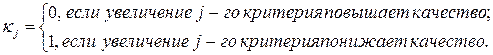
Указанный критерий возможно записать в следующем виде:
, ,
где , ( ) – суммы взвешенных нормализованных значений параметров, повышающих и понижающих уровень качества варианта частных параметров соответственно, т.е.
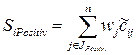 , ,
, ,
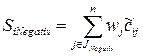 , ,
, ,
где – множество номеров частных параметров, повышающих уровень качества варианта; – множество номеров частных параметров, понижающих уровень качества варианта.
Другим решением проблемы различия направлений влияния частных параметров на уровень качества варианта есть применение дробно-рациональной формы интегрального критерия:
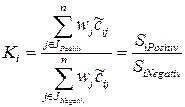 , .
, .
Увидим, что сравнение вариантов по двум вышеуказанным параметрам может дать разные результаты: лучший вариант по первому (линейному) критерию может оказаться на втором либо кроме того третьем месте по второму (дробно-рациональному) критерию. Наглядный пример приведён в следующей таблице, в которой использованы следующие обозначения: A, B, C, D – условные идентификаторы вариантов.
| Вариант | – | / | ||
| A | ||||
| B | 1,222222 | |||
| C | 1,040404 | |||
| D | 1,005005 |
Как видно из таблицы, варианты ранжируются линейным критерием в обратном порядке их перечислению, т.е. варианты занимают следующие места: 1) D; 2) C; 3) B; 4) A. В также время по дробно-рациональному критерию варианты ранжируются в порядке их перечисления: 1) A; 2) B; 3) C; 4) D.
Конечно, появляется вопрос: какой же критерий более «объективен»? Ответ легко взять, трактуя сумму как сумму вкладов, имеющихся на ваших квитанциях, а – как сумму ваших долгов. Наряду с этим значение линейного критерия – это или превышение запасов над долгом (в случае, если ), или забранная со знаком минус величина фактического долга (в случае, если ). Так – это в полной мере содержательно трактуемая величина.
Значение же дробно-рационального критерия – это количество ваших запасенных рублей, приходящихся на один рубль долга. Разумеется, что это, не смотря на то, что и занимательный, но слишком мало информативный показатель. Единственно, что возможно узнать по этому показателю – имеет ли место задолженность либо запасы превышают неспециализированный долг, но сама величина долга-превышения неизвестены. Эту же данные возможно взять и из критерия , потому, что честны отношения:
( ) « ( );
( ) « ( ).
Оба эквивалентных неравенства первого отношения означают, что сумма задолженностей не превышает суммы запасов. Подобно, эквивалентные неравенства второго отношения означают наличие настоящего долга. Но отношение не показывает безотносительную величину настоящего долга либо превышения запасов над долгами.
Изложенное разрешает сделать вывод о преимуществе линейного критерия перед дробно рациональным. Дробно-рациональный критерий возможно применять как дополнительный в том случае, если окажется пара вариантов с однообразными значениями линейного критерия.
8 Расчёт весовых коэффициентов
частных параметров
Вариант линейной организации параметров
Совокупность названий частных параметров – это, по сути дела, простое множество вербальных значений, исходя из этого весовые коэффициентов параметров возможно установить посредством уже рассмотренной ранее (см. п. 3) процедуры определения весов, основанной на применении таблицы парных сравнений, заполняемой баллами предпочтений.
При громадном количестве частных параметров возможно применять и более несложную, но не меньше действенную процедуру, основанную на парном сравнении всех вариантов с единственным – базисным критерием. Базисным критерием возможно любой из частных параметров, к примеру, первый по номеру. Но все же, целесообразнее применять в качестве базисного самый «важный» критерий. Потом без сокращения общности будем предполагать, что базисный критерий учитывается под первым номером.
Сравнивать варианты целесообразно, так же, как и прежде, в рамках девятибалльной шкалы Саати. В следствии сравнения формируется вектор результатов , где – итог сравнения -го и первого частных параметров. Семантически представляет собой интуитивно оцениваемое отношение степени важности (значимости, полезности) -го частного критерия к степени важности базисного критерия т.е это интуитивная оценка величины 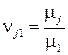 , где , – очевидно не оцениваемые степени важности для ЛПР -го и первого частных параметров.
, где , – очевидно не оцениваемые степени важности для ЛПР -го и первого частных параметров.
Формула весовых коэффициентов наряду с этим имеет форму:
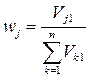 , .
, .
Для разглядываемого примера вероятный вариант расчёта весовых коэффициентов представлен в таблице 12.
Разглядывая таблицу 12, возможно подметить следующее:
1) личный критерий «Расход горючего на 100 км» был самый важным для ЛПР; данный показатель качества взял громаднейший весовой коэффициент; его значимость для ЛПР существенно (в 9 раз) превышает значимость частного критерия «Год выпуска», выбранного в качестве базы для сравнения частных параметров.
2) наименее значимыми для ЛПР были частные критерии «Тип привода» и «Объём двигателя» («Привод»).
8.2 Иерархическая организация параметров.
Уникальный способ Саати
В случае, если количество учитываемых частных параметров громадно, то целесообразно организовать критерии в иерархию, на верхних уровнях которой размещаются группы параметров, а на последнем уровне – фактически критерии. Такая организация разрешает более шепетильно оценить весовые коэффициенты параметров.
Главные идеи уникального способа Саати таковы.
1. Строится иерархия частных параметров: 1) на нулевом уровне размещается наименование всей иерархической совокупности, к примеру, «Критерии для выбора автомобиля»; 2) на последующих уровнях – с первого по ( -1)-й уровни размещаются группы параметров; 3) на -м уровне размещаются фактически критерии; 4) на маргинальном – -м уровне размещаются сопоставляемые варианты; в отечественном примере сопоставляемыми вариантами являются конкретные машины, из которых ЛПР выбирает самый подходящий вариант. Наряду с этим все критерии не имеют значений – это легко лингвистические метки, имеющие некую семантику качественного показателя без деления этого показателя на какие-либо уровни.
2. На каждом уровне иерархии происходит сравнение элементов этого уровня между собой. Причём сравнение выполняется пара раз: столько, сколько элементов содержится на прошлом уровне. Каждое сравнение осуществляется «с позиции» одного из элементов прошлого уровня, что выступает в роли критерия, по которому попарно сравниваются элементы текущего уровня.
3. Все группы параметров, фактически критерии и варианты сравниваются между собой по шкале 1..9 по схеме «любой с каждым», результаты сравнения представляются в виде матрицы парных сравнений. По каждой матрице парных сравнений формируется вектор весовых коэффициентов. Для большей научности способа Саати рекомендует вычислять весовые коэффициенты как личный вектор матрицы парных сравнений, соответствующий солиднейшему собственному числу данной матрицы. Особенной неприятности вычисления этого собственного вектора нет, но и особенной потребности в его вычислении также нет: в случае, если нормализовать элементы столбцов матрицы парных сравнений их суммами, а после этого усреднить результаты, приобретаемые в каждой строке, то итог будет очень близок к собственному вектору Саати.
4. Итак, по каждой матрице парных сравнений взят отдельный вектор весовых коэффициентов – по количеству учитываемых параметров. Их возможно разместить в виде столбцов последовательно приятель за втором и взять целую матрицу весовых коэффициентов. Как же по данной совокупности матриц, составленных из векторов весовых коэффициентов возможно взять единственный вектор весовых коэффициентов, ранжирующих сопоставляемые варианты? Для этого необходимо вычислить произведение матриц, синтезированных из векторов весовых коэффициентов, взятых на каждом уровне иерархии:
= ´ ´¼´ ´ =
= ´ ´¼´ ´ = (1)
где = – матрица -го уровня, – составленная из столбцов весовых коэффициентов, вычисленных для элементов этого уровня с позиции каждого из элементов прошлого уровня; – количество уровней иерархии, на которых размещаются группы параметров (эти уровни имеют номера 0.. ); – количество учитываемых частных параметров – число элементов критериального уровня иерархии с номером ; (увидим, что количество учитываемых частных параметров имеет и более простое обозначение , исходя из этого ); – количество сопоставляемых вариантов – число элементом вариантного уровня иерархии с номером . Потому, что в (1) обозначает количество элементов -го уровня иерархии, то имеет место равенство: .
Разглядывая формулу для вычисления вектора , направляться чётко осознавать следующее. Матрица -го уровня ( ) имеет столько строчков, сколько элементов содержится на этом -м уровне и столько столбцов, сколько элементов содержится на прошлом -м уровне; благодаря этого произведение любой пары матриц формулы (1) вычисляемо, и результатом вычисления есть новая матрица число строчков которой равно строчков левой из пары перемножаемых матриц, а число столбцов – числу столбцов правой из пары перемножаемых матриц. Результатом перемножения всех матриц (1) есть вектор (одностолбцовая матрица), содержащий весовые коэффициентов сопоставляемых вариантов.
8.3 Модифицированный способ Саати
для иерархии параметров, имеющих значения
В целом, способ Саати применим и при параметров со значениями, отличие будет состоять лишь в методе формирования матрицы — го – вариантного – уровня иерархии = . В разглядываемом нами случае параметров со значениями элементы матрицы не оцениваются посредством матрицы парных сравнений, а просто вычисляются по формуле:
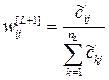 , , , (2)
, , , (2)
где – нормализованное значение -го критерия для -го варианта. Конечно, формулы (2) может употребляться лишь , если все частные критерии имеют числовые значения, т.е. предварительно нужно осуществить взвешивание значений всех вербальных параметров.
В остальном предлагаемый модифицированный способ абсолютно сходится с хорошим способом Саати: 1) так же строится иерархия, складывающаяся из групп параметров в вершинах и частными параметрами в концевых вершинах (в страницах) дерева иерархии; 2) так способом парных сравнений оцениваются весовые коэффициенты групп и фактически параметров; 3) так же по формуле (1) вычисляются весовые коэффициенты вариантов; 4) так же полученные весовые коэффициенты вариантов употребляются для ранжирования этих вариантов, т.е. в качестве значений интегрального критерия, т.е. вектор значений интегрального критерия сходится с вектором весовых коэффициентов: .
Как уже отмечалось, отличие состоит лишь в методе вычисления весовых коэффициентов на маргинальном – вариантном уровне иерархии.
Разглядываемый вариант способа Саати, по сути дела, эквивалентен способу интегрального критерия с линейной формой интегрального критерия. Эта эквивалентность отражается следующей теоремой.
Теорема. Способ Саати для случая частных параметров со значениями эквивалентен (в плане ранжирования вариантов) способу интегрального критерия uс линейной формой интегрального критерия, vкоэффициенты которой вычисляются по схеме Саати – при помощи их сравнений групп и парных критериев в рамках намерено синтезируемой иерархии, wи нормализацией параметров суммами их вариантных значений, xпредварительно при необходимости смещённых в область положительности yи сориентированных в направлении увеличения интегрального качества. zПри этом константа смещения частных параметров в способ положительности переориентации {и область значений параметров, понижающих уровень качества вариантов, влияние на итог ранжирования вариантов не оказывают.
9 Выбор варианта по способу Саати для иерархии параметров, имеющих значения
Лучший вариант выбирается из таблицы вариантов множества Парето следующим образом:
1) лучший вариант по вектору весовых коэффициентов , отысканному в следствии синтеза иерархии параметров: выбирается вариант с громаднейшим значением весового коэффициента;
2) в случае, если находится единственный лучший вариант, то ответ задачи получено;
3) в случае, если узнается, что пара вариантов являются эквивалентными по весовым коэффициентам, то лучший вариант выбирается по жребию.
Для разглядываемого примера кроме стандартного комплекта таблиц (1 – 11) приведены следующие сведения, отражающие специфику способа Саати:
1) рисунок 1 с иерархией параметров; организован лишь один уровень групп параметров «Технические», «Эргономические и другие» и «Экономические»;
2) таблица 12 с вектором результатов парных сравнений групп параметров и вектором весовых коэффициентов этих групп;
3) таблица 13 с вектором результатов парных сравнений параметров с позиций выделенных групп параметров;
4) таблица 14 с векторами значений весовых коэффициентов параметров, организованными по векторам результатов парных сравнений;
5) таблица 15 с вектором итоговых весовых коэффициентов параметров, взятым путём умножения матрицы таблицы 14 на вектор коэффициентов таблицы 12;
6) таблица 16, содержащая таблицу множества Парето с однонаправленными и нормализованными значениями частных параметров, весовые их ранги и коэффициенты вариантов.
Таблица 1. Таблица исходных вариантов
| Номер варианта | Наименование автомобиля | Год выпуска | Количество двиг. | Разгон до 100 км | Привод | Кузов | Число дверей | Цена | Цвет | Страна | Горючее на 100 км | Показатель удаления |
| Mazda 3 | 1.6 | передний | седан | светло синий | Япония | 2,3,8,9 | ||||||
| Volkswagen Touareg | 3.6 | 7.5 | смешанный | универсал | красный | Германия | ||||||
| Toyota Camry | 2.4 | передний | седан | серебристый | Япония | |||||||
| Ford Focus | 1.6 | 10.2 | передний | седан | 558 000 | красный | Российская Федерация | 2,3,10 | ||||
| Audi A6 | 2.8 | передний | седан | белый | Германия | |||||||
| Nissan Teana | 2.5 | передний | седан | тёмный | Япония | |||||||
| BMW X 5 | 3.0 | 6.5 | полный | хэтчбек | светло синий | Германия | ||||||
| Mercedes-benz ML 350 | 3.5 | полный | фастбек | серый | США | 8,9,11 | ||||||
| RANGE ROVER VOGUE | 4.0 | полный | фастбек | темно-светло синий | Англия | 8,9,11 | ||||||
| RENO LOGAN | 1.6 | передний | седан | фисташковый | Российская Федерация | 2,9,10 | ||||||
| Ограничения | =2000 | =2.0 | * | * | =4 | {красный, тёмный, белый, серебристый, светло синий} | НЕ {Российская Федерация, Китай} |
Таблица 2. Таблица допустимых вариантов
| Номер варианта | Наименование автомобиля | Год выпуска | Количество двиг. | Разгон до 100 км/час | Привод | Кузов | Число дверей | Цена | Цвет | Страна | Горючее на 100 км | Показатель удаления |
| Volkswagen Touareg | 3.6 | 7.5 | полный | универсал | красный | Германия | ||||||
| Toyota Camry | 2.4 | передний | седан | серебристый | Япония | |||||||
| Audi A6 | 2.8 | задний | седан | белый | Германия | |||||||
| Nissan Teana | 2.5 | передний | седан | тёмный | Япония | |||||||
| BMW X 5 | 3.0 | 6.5 | полный | хэтчбек | светло синий | Германия |
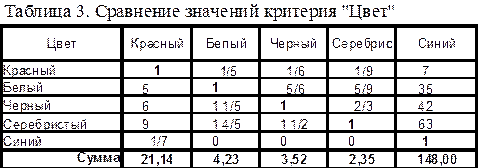
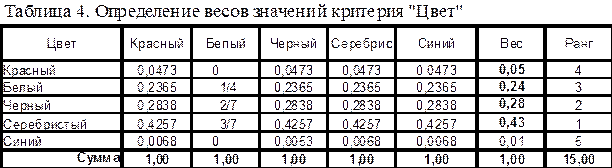
Таблица 5. Сравнение значений критерия «Привод» Таблица 6. Веса значений критерия «Привод»
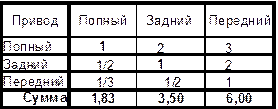
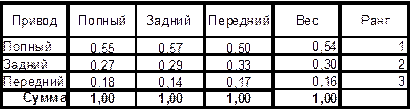
Таблица 7. Сравнение значений критерия «Кузов» Таблица 8. Веса значений критерия «Кузов»
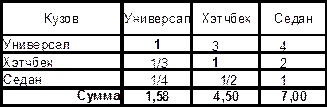
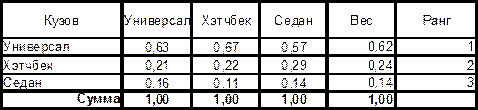
Таблица 9. Веса значений критерия «Страна»
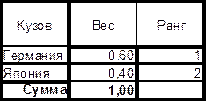
Таблица 10. Таблица множества Парето с оцифрованными значениями вербальных параметров
| Номер варианта | Наименование автомобиля | Год выпуска | Количество двиг. | Разгон до 100 км/час | Привод | Кузов | Число дверей | Цена | Цвет | Страна | Горючее на 100 км |
| Volkswagen Touareg | 3,6 | 7,5 | 0,539 | 0,6232 | 0,0473 | 0,6 | |||||
| Toyota Camry | 2,4 | 0,16 | 0,1373 | 0,4257 | 0,4 | ||||||
| Audi A6 | 2,8 | 0,2972 | 0,1373 | 0,2365 | 0,6 | ||||||
| BMW X 5 | 6,5 | 0,539 | 0,2395 | 0,0065 | 0,6 | ||||||
| Среднее значение | 2004,25 | 2,95 | 0,3847 | 0,2843 | 4,5 | 0,1789 | 0,55 |
Таблица 11. Таблица множества Парето со словесными значениями вербальных параметров
| Номер варианта | Наименование автомобиля | Год выпуска | Количество двиг. | Разгон до 100 км/час | Привод | Кузов | Число дверей | Цена | Цвет | Страна | Горючее на 100 км | Показатель удаления |
| Volkswagen Touareg | 3,6 | 7,5 | полный | универсал | красный | Германия | ||||||
| Toyota Camry | 2,4 | передний | седан | серебристый | Япония | |||||||
| Audi A6 | 2,8 | задний | седан | белый | Германия | |||||||
| BMW X 5 | 3,0 | 6,5 | полный | хэтчбек | светло синий | Германия |
Частные критерии