Резонансными режимами в цепях синусоидального тока именуются такие режимы, при которых сдвиг фаз ? между напряжением на участке цепи и током равен нулю.
В цепи с последовательным соединением элементов R, L, C сдвиг фаз между напряжением на зажимах участка цепи и током определяется через сопротивления этого участка цепи:
.
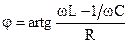Он делается равным нулю при равенстве реактивных сопротивлений . Напряжения на индуктивности и емкости равны между собой (рис. 2.9,б), исходя из этого резонанс в разглядываемой цепи именуют резонансом напряжений. Входное напряжение наряду с этим равняется напряжению на активном сопротивлении.
Из условия происхождения резонансного режима направляться метод его успехи. Резонанс напряжений в цепи возможно взять методом трансформации одной из трех размеров при постоянстве двух вторых:
1) f = var, L = const, C = const;
2) f = const, L = var, C = const;
3) f = const, L = const, C = var.
Характеристики, показывающие изменение напряжений, токов и других размеров при трансформации одного из параметров, именуются резонансными чертями.
Разглядим резонансные кривые тока I(?), напряжений на индуктивности и емкости UL(?) и UC(?) и угла сдвига фаз ?(?) (рис. 2.17).
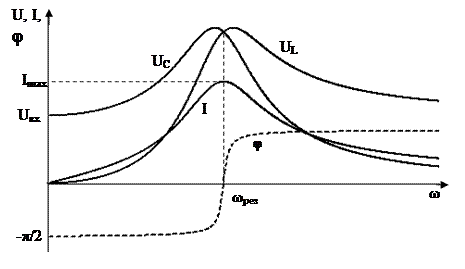
Рис. 2.17
Ток в цепи определяется законом Ома:
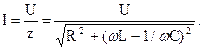
При значении частоты ? = 0 емкостное сопротивление ХС равняется бесконечности и ток в цепи равен нулю. Потом с повышением частоты емкостное сопротивление значительно уменьшается, а индуктивное возрастает и ток возрастает до большого значения при резонансе Ip = U/R. При предстоящем повышении частоты ток значительно уменьшается и при ? ?, в то время, когда индуктивное сопротивление пытается к бесконечности, он пытается к нулю.
напряжение на индуктивности определяется и собственной формой напоминает кривую зависимости тока I(?).
При ? = 0 напряжение на емкости равняется сетевому напряжению U, поскольку сопротивление конденсатора равняется бесконечности, ток в цепи отсутствует, и все входное напряжение приложено к месту разрыва. При ? = ?р напряжение емкостное равняется напряжению индуктивному. При ? ? напряжение емкостного элемента пытается к нулю.
В резонансной цепи комплексное сопротивление равняется активному сопротивлению и имеет минимальное значение Z = R = min.
Тогда ток в таковой цепи, как было продемонстрировано выше, будет иметь большое значение: IР = U/Z = U/R = Imax. Если реактивные сопротивления по величине значительно больше активного сопротивления , в режиме резонанса напряжения на индуктивности и емкости смогут многократно быть больше входное напряжение:
.
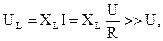
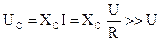Соотношение напряжений в резонансном режиме определяется величиной добротности Q контура, величина которой определяется исходя из следующих мыслей:
,
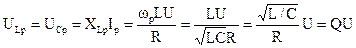где Q – добротность цепи, складывающейся из последовательно соединенных элементов R, L, C, значение которой может быть около сотен и десятков единиц.
При трансформации частоты от 0 до ?р угол сдвига фаз ? между током и напряжением изменяется от (–?/2) до 0. При трансформации частоты ? до ? угол ? возрастает от 0 до ?/2.
При параллельном соединении элементов R, L, C в цепи отмечается резонанс токов. Угол сдвига фаз между током и входным напряжением в цепи при параллельном соединении приемников определяется:
.
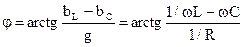Он будет равен нулю при равенстве реактивных составляющих проводимостей: либо , что и будет являться условием резонанса токов, при котором, как видно из векторной диаграммы рис. 2.12, равны реактивные составляющие токов индуктивного и емкостного элементов, входной ток равен току активного элемента и имеет минимальное значение.
Резонансные кривые (рис. 2.18) для режима резонанса токов строятся подобно резонансным кривым, выстроенным для режима резонанса напряжений.
 |
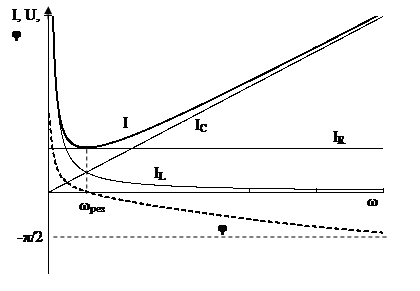Рис. 2.18
Входной ток цепи определяется в соответствии с первому закону Кирхгофа:
Ток активного сопротивления от частоты питающего напряжения не зависит и будет в любой момент неизменным.
При частоте равной нулю ток емкости равен нулю, поскольку конденсатор представляет собой разомкнутый участок цепи, а ток совершенной катушки пытается к бесконечности, поскольку при нулевой частоте катушки представляет собой короткозамкнутый участок. Входной ток при данной частоте равен току катушки и кроме этого пытается к бесконечности.
При частоте равной резонансной ?рез действующие значения емкостного и индуктивного токов равны. А так как эти токи находятся в противофазе, то их векторная сумма равна нулю, и входной ток равен току активного элемента и имеет минимальное значение.
При частоте стремящейся к бесконечности проводимость емкостного элемента пытается к бесконечности, а проводимость индуктивного элемента – к нулю. Входной ток делается фактически равным току конденсатора и кроме этого пытается к бесконечности.
При частотах меньше резонансной ?0, так как преобладает индуктивная составляющая проводимости. При частоте равной резонансной ?=?рез реактивные составляющие проводимостей равны и угол сдвига фаз равен нулю ? = 0. При частотах больше резонансной ??рез угол сдвига фаз меньше нуля ?
Примеры ответа задач
2.2.1 Записать выражение для комплексного сопротивления Z цепи (рис. 2.19) относительно зажимов а и b.
Комплексное сопротивление цепи определяется по тем же правилам, что и входное сопротивление цепи постоянного тока, лишь сопротивления всех участков записываются в комплексной форме. Наряду с этим нужно не забывать, что сопротивление активного элемента в комплексной форме записи определяется как настоящее число R, сопротивление индуктивного элемента как мнимое число j?L, а комплексное сопротивление емкостного элемента как ( ).
 |
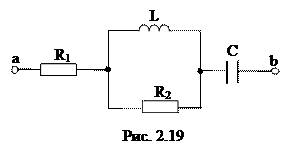Активное сопротивление R2 и индуктивная катушка соединены параллельно, тогда эквивалентное комплексное сопротивление двух параллельных ветвей определяем как:
.
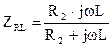Входное комплексное сопротивление всей цепи относительно зажимов а и b определим как сумму активного сопротивления R1, сопротивления реактивного сопротивления и параллельного участка емкостного элемента, поскольку все эти участки соединены последовательно:
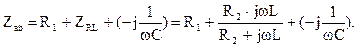
2.2.2 Чему равен угол сдвига фаз между током цепи и входным напряжением, складывающейся из а) последовательного соединения элементов R, L; б) параллельного соединения элементов R, L. Параметры элементов цепи: R = 100 Ом, L = 0,5 Гн, f = 50 Гц.
Разглядим участок цепи, складывающийся из последовательного соединения элементов R, L (рис. 2.20, а). Выстроим векторную диаграмму напряжений и тока на каждом из элементов этого участка. Так как по всем элементам протекает одинаковый ток I, то при построении векторной диаграммы эргономичнее всего принять его начальную фазу за ноль.
 |
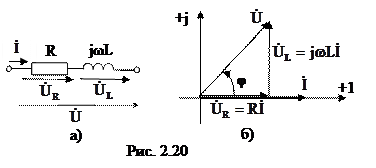Напряжение на активном сопротивлении сходится по фазе с током, а напряжение на индуктивном реактивном сопротивлении опережает ток по фазе на угол 90º, и исходя из этого на векторной диаграмме вектор этого напряжения развернут относительно вектора тока против часовой стрелки на угол 90º. Напряжение на зажимах всего участка равняется геометрической сумме векторов напряжений UR и UL. Угол сдвига фаз между током и напряжением этого участка, как видно из выстроенной векторной диаграммы (рис. 2.20, б), возможно выяснить из отношения напряжений и он зависит от соотношения активного и реактивного сопротивлений:
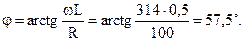
Разглядим параллельное соединение этих же элементов (рис. 2.21, а). При таком соединении напряжение ветвей, соединенных параллельно, одинаково, исходя из этого при построении векторной диаграммы комфортно принять за ноль начальную фазу напряжения на зажимах цепи, а векторы токов строить довольно этого напряжения.
 |
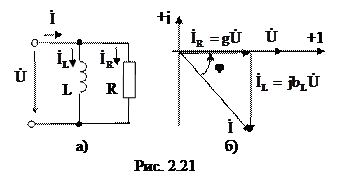Ток активного элемента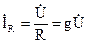 
сходится с напряжением по фазе и на векторной диаграмме находится параллельно вектору напряжения. Ток реактивного индуктивного элемента 
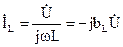отстает от напряжения по фазе на угол 90º, и на векторной диаграмме вектор этого тока повернут относительно вектора напряжения по часовой стрелке на 90º. Угол сдвига фаз между током и напряжением этого участка, как видно из выстроенной векторной диаграммы (рис. 2.21, б), возможно выяснить из отношения токов и он зависит от соотношения активной и реактивной проводимостей:
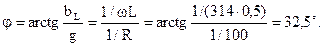
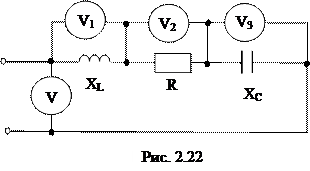
2.2.3 Выяснить показания вольтметра, подключенного к входным зажимам цепи (рис. 2.22), при условии, что показания остальных вольтметров, измеряющих действующие значения напряжений, заданы: UV1 = 50 В, UV2 = 40 В, UV3 = 20 В. При ответе большинства задач по расчету цепей синусоидального тока комфортно ответ сопровождать построением векторных диаграмм. Для удобства ответа данной задачи выстроим векторную диаграмму напряжений и тока цепи на каждом из ее элементов (рис. 2.23). Начальную фазу тока примем равной нулю.
 |
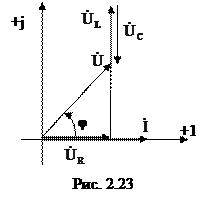
Напряжение на активном сопротивлении сходится с током по фазе, напряжение на индуктивной катушке опережает ток по фазе на угол 90º, а напряжение на емкостном элементе отстает от тока на угол 90º. Напряжение на зажимах цепи равняется геометрической сумме векторов напряжений всех элементов и возможно выяснено посредством теоремы Пифагора из взятого треугольника напряжений:
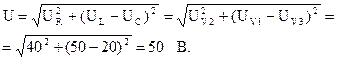
2.2.4 В цепь синусоидального тока включены последовательно элементы R, L, C (рис. 2.24). Каким должно быть сопротивление емкостного элемента ХС, дабы при замыкании рубильника показания амперметра не изменялись.
Заданы параметры цепи R = 8 Ом, XL = 6 Ом.
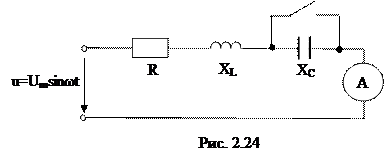
Амперметр измеряет действующее значение тока, протекающего в цепи, что определяется в соответствии с закону Ома:
.
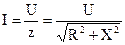Так как на вход цепи подается неизменное напряжение, то действующее значение тока цепи не будет изменяться, в случае, если будет оставаться неизменным при замыкании ключа полное сопротивление цепи, которое возможно записать:
.
При замыкании ключа емкостное сопротивление исключается из цепи и в цепи остается лишь индуктивное реактивное сопротивление. Чтобы полное сопротивление осталось неизменным, нужно дабы модуль суммарного реактивного сопротивления схемы до замыкания и по окончании замыкания ключа не изменялся:
а такое допустимо лишь в том случае в случае, если емкостное сопротивление увеличится в два раза индуктивного:
2.2.5 В цепь синусоидального тока (рис. 2.25) включены три амперметра электромагнитной совокупности. Выяснить показания амперметра А2, в случае, если амперметры А и А1 показывают соответственно 10 А и 6 А.
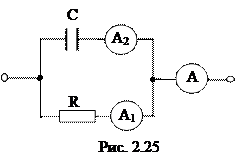Амперметры измеряют действующие значения синусоидальных токов.
Для удобства ответа задачи как следует выстроим векторную диаграмму (рис. 2.26) токов и напряжений цепи.
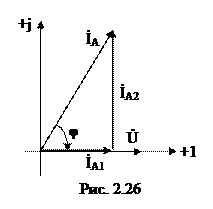Цепь складывается из двух параллельно соединенных ветвей. Примем начальную фазу напряжения на зажимах этих ветвей равной нулю. Ток активного сопротивления сходится с этим напряжением по фазе, а ток емкостного сопротивления опережает напряжение по фазе на угол 90º. Входной ток равен геометрической сумме этих векторов. Полученная векторная диаграмма представляет собой прямоугольный треугольник, именуемый треугольником токов. Длины сторон этого треугольника, соответствующие действующим значениям токов ветвей связаны выражением, записанным на основании теоремы Пифагора:
, откуда
2.2.6 Вычислить напряжения и токи на всех участках электрической цепи, схема которой продемонстрирована на рис. 2.27, питающейся от источника синусоидального напряжения, комплексное действующее значение которого Выстроить векторную диаграмму вычисленных токов и напряжений. Параметры элементов цепи: R =XL =XC = 100 Ом.
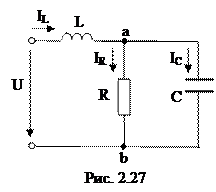Чтобы по закону Ома выяснить ток на входе цепи, нужно вычислить комплексное сопротивление цепи довольно входных зажимов. Активное и емкостное сопротивления соединены параллельно, исходя из этого эквивалентное сопротивление относительно зажимов «ab» возможно вычислить:
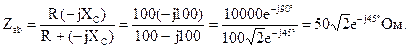
Довольно входных зажимов сопротивление участка и индуктивное сопротивление «ab» соединены последовательно, исходя из этого входное сопротивление всей цепи возможно выяснить как сумму комплексных сопротивлений:
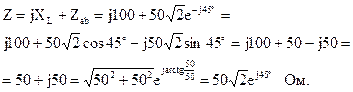
Определим входной ток, протекающий по индуктивному элементу:
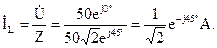
Определим напряжения на участках цепи:
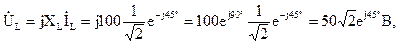
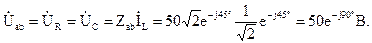
Зная напряжения на зажимах параллельных ветвей, возможно выяснить токи, протекающие по ветвям по закону Ома:
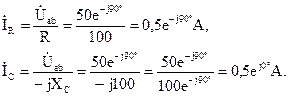
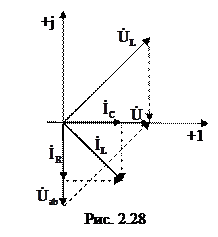Выстроим векторную диаграмму токов и напряжений участков цепи (рис. 2.28). Для этого на комплексной плоскости в соответствующих масштабах тока mi и напряжения mu выстроим вектора вычисленных напряжений и токов со собственными начальными фазами. На векторной диаграмме продемонстрируем исполнение законов Кирхгофа:
,
2.2.7 Вычислить напряжения и токи на всех участках
 |
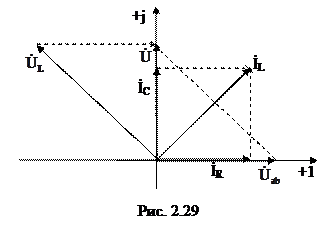электрической цепи, схема которой продемонстрирована на рис. 2.27, в случае, если известен ток ветви с активным сопротивлением IR = 2 A. Выстроить векторную диаграмму вычисленных токов и напряжений.
Параметры элементов цепи: R =XL =XC = 100 Ом.
Примем начальную фазу тока ветви с активным сопротивлением равной нулю, тогда комплексное значение этого тока запишется:
Зная ток в одной из параллельных ветвей, отыщем напряжение на зажимах этих ветвей по закону Ома:
Зная напряжение на зажимах параллельных ветвей, легко отыщем ток в ветви с конденсатором:
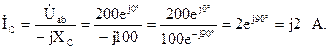
Ток в неразветвленной части цепи отыщем, составив уравнение по первому закону Кирхгофа для узла «а»:
Напряжение на зажимах первой ветви, содержащей индуктивный элемент, отыщем по закону Ома:
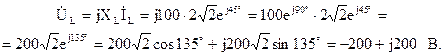
Напряжение на зажимах цепи отыщем, составив уравнение по второму закону Кирхгофа:
Выстроим векторную диаграмму вычисленных токов и напря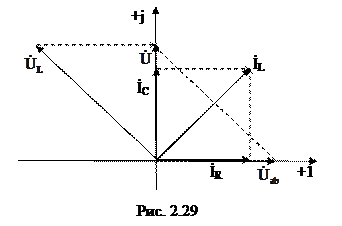 
жений на рис. 2.29.
Напряжения и токи в выбранных масштабах будем строить на векторной диаграмме в том порядке, в котором создавали их расчет.
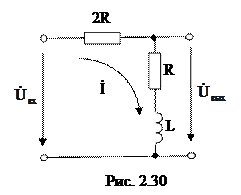2.2.8 Вычислить комплексную передаточную функцию по напряжению и выстроить АЧХ для цепи, схема которой приведена на рис. 2.30.
Передаточная функция по напряжению определяется отношением выходного напряжения цепи в режиме холостого хода к входному напряжению, записанных в комплексной форме:
,
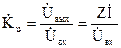где I – комплексное действующее значение тока, вызываемое в цепи входным напряжением , причем все элементы в разглядываемой цепи соединены последовательно и по ним протекает одинаковый ток; Z – комплексное сопротивление участка цепи, с которого снимается выходное напряжение .
По закону Ома ток определяется:
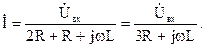
Так как сопротивление , то комплексную передаточную функцию возможно выяснить:
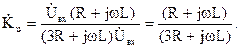
Модуль передаточной функции определяется:
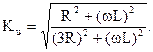
При частоте ? = 0 модуль передаточной функции Ku =1/3;
при частоте ? ? модуль передаточной функции Ku = 1. Эти значения определяют темперамент трансформации АЧХ, которая приведена на рис. 2.31.
 |
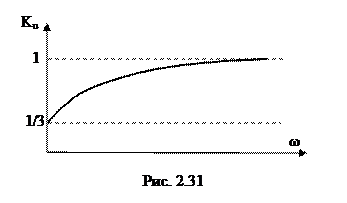2.2.9 Найти значение емкости тока и конденсатора в цепи, складывающейся из последовательного соединения элементов R, L, C (рис. 2.22) при условии, что в цепи режим резонанса напряжений.
Заданы параметры цепи: U= 50 B, R = 100 Ом, L = 0,1 Гн, частота питающей сети f = 50 Гц.
Условием резонанса напряжений есть равенство реактивных сопротивлений индуктивного и емкостного элементов: либо , из этого выражения возможно взять значение емкости конденсатора, при котором в цепи наступит режим резонанса напряжений:
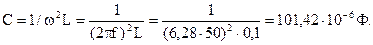
Полное сопротивление цепи при резонансе равняется активному сопротивлению, поскольку реактивные индуктивное и емкостное сопротивления равны по модулю и их сумма равна нулю:
Тогда действующее значение тока в цепи будет равняется:
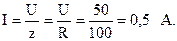
2.2.10 Для электрической цепи, схема которой приведена на рис. 2.32, составить на базе законов Кирхгофа совокупность уравнений для расчета токов в ветвях цепи и записать ее в двух формах: дифференциальной и символической.
 |
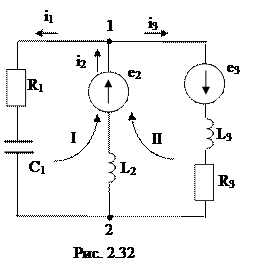Так как схема содержит пара источников электроэнергии, хорошие направления токов в ветвях выбираем произвольно. Кроме этого произвольно выбираем направления обхода контуров.
Число уравнений, составляемых по законам Кирхгофа, должно соответствовать количеству малоизвестных токов. Разглядываемая электрическая цепь имеет три ветви с малоизвестными токами, исходя из этого совокупность уравнений, составляемая по законам Кирхгофа обязана складываться из трех уравнений.
По первому закону Кирхгофа составляется на одно уравнение меньше, чем количество узлов в цепи. Цепь имеет два узла, исходя из этого по первому закону Кирхгофа составляем одно уравнение. Недостающие два уравнения составляем по второму закону Кирхгофа для двух свободных контуров, направление обхода которых продемонстрировано на рис. 2.32.
Запишем совокупность уравнений в дифференциальной форме записи, где все токи, напряжения и ЭДС записаны в зависимости и мгновенной форме между токами и напряжениями реактивных элементов дифференциально-интегральные:
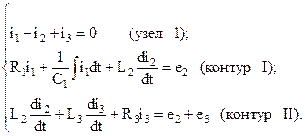
Запишем совокупность уравнений в символической форме записи. Для этого от функций времени перейдем к изображению синусоидальных функций времени комплексными числами. Соответственно дифференциальные и интегральные зависимости между токами и напряжениями в цепях синусоидального тока мы заменяем линейными зависимостями между напряжениями и комплексными токами:
|
 
|
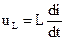
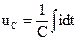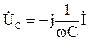
Тогда совокупность уравнений, записанная по законам Кирхгофа будет иметь вид:
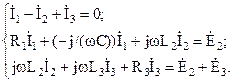
2.2.11 Вычислить токи в ветвях цепи, схема которой представлена на рис. 2.32, способом узловых потенциалов. Выстроить векторную диаграмму токов и напряжений на всех элементах цепи. Параметры элементов цепи:
R1 =80 Ом, R3 =60 Ом, L2 =40 мГн, L3 =30 мГн, C1 =10 мкФ.
Расчет цепи будем делать в комплексной форме записи, для чего перейдем от ЭДС, записанных как функции времени, к их изображению комплексными числами:
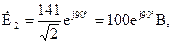
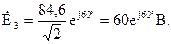
Вычислим комплексные сопротивления ветвей:
 |
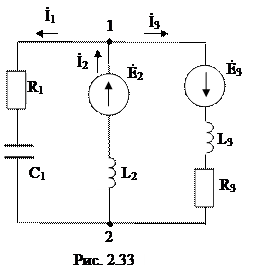Произвольно выбранное направление токов в ветвях схемы продемонстрировано на рис. 2.33. Так как схема имеет всего два узла, то для расчета токов в ней используют частный случай способа узловых потенциалов – способ двух узлов. В соответствии с этому способу напряжение между узлами 1 и 2 определяется:
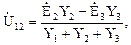
где комплексные проводимости параллельных ветвей:
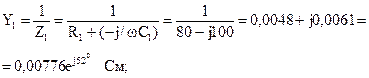
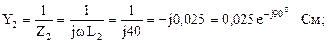
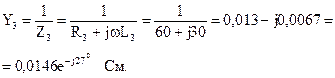
Подставим значения комплексных ЭДС и проводимостей в формулу для определения напряжения:
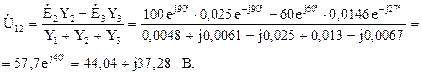
Вычислим токи в ветвях цепи, пользуясь законом Ома для ветви с ЭДС:
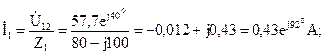
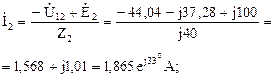
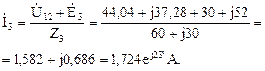
Для построения векторной диаграммы вычислим напряжения на всех элементах цепи:
 |
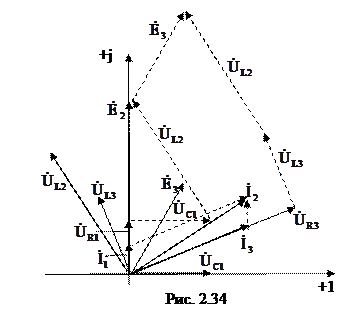На комплексной плоскости выстроим векторную диаграмму токов и напряжений (рис. 2.34) и продемонстрируем на ней исполнение законов Кирхгофа, другими словами:
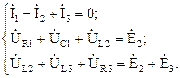
2.2.12 Записать мгновенные значения тока напряжения и первой ветви на ее зажимах согласно данным задачи 2.2.11. Выстроить временные зависимости этих функций в одних осях координат.
В следствии расчетов в комплексной форме были взяты напряжения и значения тока:
В мгновенной форме напряжение и ток возможно записать:
 |
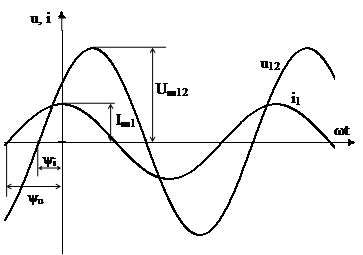Рис. 2.35
Выстроим временные диаграммы этих синусоидальных функций. При построении временных диаграмм нужно не забывать, что в случае, если синусоида имеет ненулевую начальную фазу, то она смешается относительно начала координат:
при начальной фазы больше нуля ? 0 – влево;
при начальной фазы меньше нуля ? 0 – вправо.
Временные диаграммы заданных синусоидальных функций выстроены на рис. 2.35.
ТРЕХФАЗНЫЕ ЦЕПИ
Базы теории