Математика
Множества.
Определение множества.
Множество это совокупность объектов, объедененные по определенному показателю N, Z, R.
Безлюдным именуется множество которое не содержит ни одного элемента.
Два множества именуются равными, если они складываются из одних и тех же элементов.Х=У в случае, если х пренадлежит Х.
Множества именуют замкнутыми в случае, если границы принадлежат ему, в противном случае открыты.
Множества бывают конечными и нескончаемыми. Конечное множество определяется конечными границами.
Множества Х ограничено сверху(снизу), в случае, если существует точка числа d.
2) Операции над множеством
— Объеденение Х и У именуется множеством Z складывающееся из всех элементов, которыми владел хотя бы одной из множеств Х и У
— Пересечение Х и У именуют множеством Z, складывающееся из всех элементов принадлежащих каждому множеству из Х и У .
— разностью множеств Х и У именуют множество Z складывающихся из всех элементов Х не принадлежащих У
— Дополнением (Х) Х под универсально объеденяющим множестве И, именуется множество И не принадлежащих Х.
3) Последовательности
Опр. В случае, если каждому числу n изнатурального последовательности, поставлено соответствующее настоящее число xn , то множество настоящих чисел х1,х2….хn именуют числовой последовательностью.
Опр. Число а именуют пределом последовательности {xn} , в случае, если для любого E0 существует номер N зависящий от Е (существует N= N(E))
4) Монотонные и ограниченные последовательности.
Монотонная последовательность — это последовательность, элементы которой с повышением номера не убывают, либо, напротив, не возрастают. Последовательность из одного числа не имеет возможности принимать во внимание возрастающей либо убывающей.
Последовательность именуется ограниченной сверху, в случае, если существует такое число U, что для любых номеров n. Наряду с этим число U именуется верхней границей последовательности.
Последовательность именуется ограниченной снизу, в случае, если существует такое число L, что для любых номеров n. Число L именуется нижней границей последовательности.
Последовательность именуется ограниченной, в случае, если существуют такие числа L и U, что для всех n = 1,2,3,…
теорема о ограниченности и связи монотонности
5) Сходящиеся последовательности.
Опр. Сходящейся именуется последовательность, которая имеет предел в противном случае это будет расходящееся последовательность.
Свойство сходящей последовательности.
1. Сходящ. последоват. Имеет лишь один предел.
2. Сход. Послед. Ограничена
3. Сумма (разность) сход. Послед. Имеется сходящая последовательность , предел которой равен сумме(разности) сходящих последовательностей.
4. Предел произведений Х и У сходящийся последовательности будет равен произведению пределов этих последовательностей.
5. Пускай Х и У сходящ. послед. , причем { } не равен нулю, тогда
6) Функции одной переменной.
Понятие функции.
Опр. Функция Х= фи(у) = f в -1 степени(у) именуют обратной функцией f(x).
Опр. Пускай у= f(u), где u в собственности U, u= фи (x), где х в собственности Х. Тогда у= f(фи(х)) заданная на х именуется сложной .
Пример: у= синус 2х.
Главные функции
1 константа у=с
2 степенная у=х в степени а
3 показательная у=а в степени х
4 логарифмическая у= логарифм n по основанию а, а больше 0, а не равен 1.
5 триногонометрические у= синус х, у= косинус х.
6 обратные триногонометрические y=arcsin x, y= arcos x.
Опр. Элементарными именуют функции, каковые приобретают их главных посредством конечного числа алгебраической операции и образованной сложной функции.
7) Характеристики функции.
Опр . функция y=f(x) именуется четной, в случае, если для х в собственности Х f(-x)= f(x)
Нечетной именуют функцию в случае, если для x в собственности Х, f(x) = -f(x)
Ни четная ни нечетная именуется функция обратного вида.
Возрастающую и убывающую функцию именуют монотонной.
Опр. Функция y=f(x) ограниченная в случае, если существует (с больше 0) что для х пренадлежащего Х выполняется модуль f(x) больше либо равняется С.
Опр. Функция y=f(x) периодическая, в случае, если Т не равен 0, в случае, если существует Т не равное 0, что для любых х принадлежащих Х равняется f(x+n)= f(x).
 Предел функции в точке.
Предел функции в точке.
Опр. Число а именуется пределом функции f(x) в точке х нулевае, в случае, если f(x) определеа окресностью Х нулевое и для любого малого числа сигма больше 0, найдется число дельта больше 0 , то что для Х не равного Хнулевому , еслм модуль Х-Хнулевое меньше дельта, либо модуль f(x)-a меньше Сигма.
Опр. Пускай f(x) опрделена на промежутке (Хнулевое –дельта, до Хнулевого) где дельта больше 0, тогда число а именуется пределом f(x) слева от точки Хнулевое, в случае, если для Сигма больше 0 существует дельта больше 0, что для всех х принадлежащих( Хнулевому – дельта, до Хнулегого) выполняется (f((x)=a) больше Сигма.
Опр. F(x) выяснен на промежутке ( Хнулевого; Хнулевое +дельта), дальта больше 0, тогда а2 придел f(x) справа точкт Хнулевого, в случае, если Х( Хнулевое; Хнулевое +дельта)равносильно (f(x) –a2) меньше Сигма .
Теорема о пределах.
9) Теоремы о пределах.
10) Первый и второй превосходные пределы.
Первый превосходный предел: Существует предел Х стремящийся к 0 синус Х дроблённый на Х , в случае, если предел х стремящийся к 0 х дроблённый на синус Х =1.
Второй превосходный предел: Предел Х стремящ. К бесконечности ( 1+ 1 деленая на Х) в степени Х =е , либо предел Х стемится к бесконечности( 1+U) в степени Х =е.
11) Непрерывность функции.
Опр. F(x) постоянна в точке Хнулевое , в случае, если :
1 существует значение функции
2 существует предел функции
3 предел функции в точке равен её значению.
Опр. Точка в которой нарушено хотя бы одно условие непрерывности именуется точкой разрыва.
Опр. Точка Хнулевое именуется точкой разрыва 1-го рода, в случае, если существует конечные пределы функции в данной точке слева и справа, но они не равны между собой, или не равны значению функции в точке Хнулевое.
Опр. Точка разрыва 1-го рода именуется устраненным разрывом, в случае, если существует и равные пределы слева и справа, но f(x) либо не выяснена в точке Хнулевое либо не равна значению функции в данной точке.
Опр. Точка а именуется точкой разрыва 2-го рода f(x) в случае, если в данной точке функция не имеет по крайней мере одного из односторонних пределов либо хотя бы один из односторонних пределов нескончаем.
Функция не прерывна постоянна на промежутке Хбольшое , если она постоянна в каждой точке этого промежутка.
12) Свойства функций непрерывности в точке.
1. В случае, если f(x) и g(x) постоянны в точке Хнулевое, то f(x) +_ g(x); f(x)* g(x)
f(x) дроблённая на g(x)( при g(x) не =0) кроме этого постоянна в точке Хнулевое.
2. f(x) постоянна в точке Хнулевое и f(x) больше 0, тогда существует окресность в точке Хнулевое в которой f(x) больше 0.
3. f(u) постоянна в точке Uнулевое, и U=фи(х) постоянна в точке Хнулевое в случае, если f(фи(x))- постоянна в точке Хнулевое т.е. для постоянной ф-ции предел х стремящийся к Хнулевому f(фи(х))=f lim х стремящийся к Хнулевому фи(х).
13) Производная в точке.
Опр. Производная функции f(x) в точке Хнулевое именуется пределом отношения прирощения функции в данной точке к прирощению довода при треугольник Х пытается к 0.
Опр. Функция именуется дифференцируемой в точке Хнулевое , в случае, если в данной точке оно имеет конечную производную.
Теорема о дифференцируемости и связи непрерывности.
В случае, если f(x) диф. В точке Хнулевое , то f(x) постоянна в данной точке.
14) Правила дифференцирования.
Пускай U и V диф. В точке Хнулевое.
1 ( c+u) производная = c *u производная
2 (u+_v) проиводная = производная U + _ производная V
3 как простые производные умнодения
4 как в большинстве случаев производные деления
5 в случае, если y(u) диф. в точ. Хнулевое U=U(Хнулевое) то сложная функция производная y(x нулевое) = производ. y(u нулевое) * производная U(Хнулевое)
6 в случае, если производная y(x) не=0, то обратная функция производная Х(у)= 1 деланая на производную y(x).
15) Теоремы о дифференцируемых функциях.
Теорема Ферма
В случае, если f(х) диф. На Хбольшое и достигает громаднейшего либо мельчайшего значения в т. Хнулевое в собственности Хбольшому, то f(Хнулевое)=0
Теорема Ролля
1. F(x) – постоянна на отрезке квадрат. Скобки а;b
2. F(x) диф. На промежутке (а;b)
3. F(a) =f(b) тогда внетри отрезка существует по крайней мере одна точка
Сигма(констанат) в собственности (a;b) такая что f(сигма)=0
Теорема Лангранжа
1. F(x) постоянна на отрезке a;b
2. F(x) диф. На интеграле (a;b)
Тогда в отрезка существует по крайней мере одна т. Сигма в собственности (a;b) такая что производная f(сигма)= f(a)-f(b) дроблённые на b-a.
16) Дифференциал функции.
Пускай f(x) диф. в т. Хнулевое тогда треугольникУ =f(Хнулевое) * треугольник Х + альфа, где альфа бесконечно малое , более большого порядка чем треуг.Х при треуг.Х пытается к 0
Опр. Дифференциал функции в точке именуется произведением производной функции в точке на прирощение свободной переменной. d(y)= производная f(x)* треугольникХ
Геометрический суть- величина деф. функции равняется прирощению ординаты касательной к графику в точке (Хнулевое; Унулекой) при переходе к точке ( Хнулевое +треуг.Х равносильно f(Хнулеевое + треуг.Х)
Правило Лопиталя
Пускай функция f(x) и g(x) диф. некоей окрестности т. Хнулевое и y= производная g(x) не =0 в данной окрестности, в случае, если предел Х стреммящийся к Хнулевому f(x)= пределу Х стремящийся к Хнулевому g(x)=0 либо оба эти предела равны бесконечности, то для всех точек данной окресности выполняется равенство:
Предел Х= Хнулевому f(x) : g(x)= lim x= Хнулеваму f’(x): g’(x)
20)
21)
22)
23)
24)
25)
Тория возможности
Точные это те события , каковые непременно случатся при осуществлении комплекса условий S
Случайные именуют события каковые может или случиться или не случиться при осуществлении комплекса условий S
Неосуществимыми именуются те события , каковые заведомо известно не произ-ойдет при осуществлении комплекса условий.
Виды случайных событий
События именуют несовместными, в случае, если появление одного из них, исключает появление вторых событий в одном и том же опробовании.
Пример. Кинута монета. Появление «герба» исключает появление надписи. События «показался герб» и «показалась надпись» — несовместные.
Пара событий образуют полную группу, в случае, если в следствии опробования покажется хотя бы одно из них. Др. словами, появление хотя бы одного из событий полной группы имеется точное событие. В частности, в случае, если события, образующие полную группу, попарно несовместны, то в следствии опробования покажется одно и лишь одно из этих событий. Данный частный случай воображает громаднейший интерес для нас.
Пример. Стрелок произвел выстрел по цели. Непременно случится одно из событий: попадание, промах. Эти два несовместных события образуют полную группу.
События именуют равновозможными, в случае, если имеется основания вычислять, что ни одно из них не есть более вероятным, чем второе.
Пример. Появление того либо иного числа очков на кинутой игральной кости – равновозможные события. Вправду, предполагается, что игральная кость изготовлена из однородного материала, имеет форму верного многогранника и наличие очков не влияет на выпадение любой грани.
27) Элементарные финалы опробований
Хорошее определение возможности
Любой из вероятных результатов опробования именуют элементарным событием либо элементарным финалом.
Класическое определения связано с понятием помогающего финала.
Свойство возможности
1) Возможность точного события =1
2) Возможность неосуществимого события=0
3) Возможность случайного события – это число 0 меньше либо равен Р(А) меньше либо равняется 1
Формулы комбинаторики
Перестановками именуется комбинации складывающиеся из одной и той же совокупности n разных элементов и оличающиеся лишь порядком их размещения.
Размещениями именуются комбинации по m элементов соствленных из n разных элементов или их порядком.
Сочетаниями именуется комбинации которые содержат по m элементов состоящих их n разных элементов и отличающихся хотя бы одним элементом.
Полная несколько событий.
Событие образуют полную группу, в случае, если в следствии опробования одной их них случится непременно.
Формула полной возможности
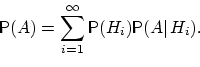
Формула Байеса
Откуда
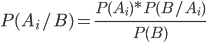
Распределение ДСВ.
Биноминальное распределение.
Проводиться серия из n опробований каждое из которых событие быть может показаться с возможностью p. В качестве ДСВ Х разглядим число показавшихся событий А в n опробованиях возможности всех вероятных значений находятся по формуле Бернулли.
Распределение Пуассона.
В случае, если n громадно , а р –мало и можно считать постоянную величину np то возможность того что событие А наступит ровно k раз в n опробованиях рассчитывается по формуле :
Pn(k)= лямда в степени k * е в степени –лямда дроблённое на k! ; лямда =np.
40) Распределение НСВ.
Математика
Множества.
Определение множества.
Множество это совокупность объектов, объедененные по определенному показателю N, Z, R.
Безлюдным именуется множество которое не содержит ни одного элемента.
Два множества именуются равными, если они складываются из одних и тех же элементов.Х=У в случае, если х пренадлежит Х.
Множества именуют замкнутыми в случае, если границы принадлежат ему, в противном случае открыты.
Множества бывают конечными и нескончаемыми. Конечное множество определяется конечными границами.
Множества Х ограничено сверху(снизу), в случае, если существует точка числа d.
2) Операции над множеством
— Объеденение Х и У именуется множеством Z складывающееся из всех элементов, которыми владел хотя бы одной из множеств Х и У
— Пересечение Х и У именуют множеством Z, складывающееся из всех элементов принадлежащих каждому множеству из Х и У .
— разностью множеств Х и У именуют множество Z складывающихся из всех элементов Х не принадлежащих У
— Дополнением (Х) Х под универсально объеденяющим множестве И, именуется множество И не принадлежащих Х.
3) Последовательности
Опр. В случае, если каждому числу n изнатурального последовательности, поставлено соответствующее настоящее число xn , то множество настоящих чисел х1,х2….хn именуют числовой последовательностью.
Опр. Число а именуют пределом последовательности {xn} , в случае, если для любого E0 существует номер N зависящий от Е (существует N= N(E))
4) Монотонные и ограниченные последовательности.
Монотонная последовательность — это последовательность, элементы которой с повышением номера не убывают, либо, напротив, не возрастают. Последовательность из одного числа не имеет возможности принимать во внимание возрастающей либо убывающей.
Последовательность именуется ограниченной сверху, в случае, если существует такое число U, что для любых номеров n. Наряду с этим число U именуется верхней границей последовательности.
Последовательность именуется ограниченной снизу, в случае, если существует такое число L, что для любых номеров n. Число L именуется нижней границей последовательности.
Последовательность именуется ограниченной, в случае, если существуют такие числа L и U, что для всех n = 1,2,3,…
теорема о ограниченности и связи монотонности
5) Сходящиеся последовательности.
Опр. Сходящейся именуется последовательность, которая имеет предел в противном случае это будет расходящееся последовательность.
Свойство сходящей последовательности.
1. Сходящ. последоват. Имеет лишь один предел.
2. Сход. Послед. Ограничена
3. Сумма (разность) сход. Послед. Имеется сходящая последовательность , предел которой равен сумме(разности) сходящих последовательностей.
4. Предел произведений Х и У сходящийся последовательности будет равен произведению пределов этих последовательностей.
5. Пускай Х и У сходящ. послед. , причем { } не равен нулю, тогда
6) Функции одной переменной.
Понятие функции.
Опр. Функция Х= фи(у) = f в -1 степени(у) именуют обратной функцией f(x).
Опр. Пускай у= f(u), где u в собственности U, u= фи (x), где х в собственности Х. Тогда у= f(фи(х)) заданная на х именуется сложной .
Пример: у= синус 2х.
Главные функции
1 константа у=с
2 степенная у=х в степени а
3 показательная у=а в степени х
4 логарифмическая у= логарифм n по основанию а, а больше 0, а не равен 1.
5 триногонометрические у= синус х, у= косинус х.
6 обратные триногонометрические y=arcsin x, y= arcos x.
Опр. Элементарными именуют функции, каковые приобретают их главных посредством конечного числа алгебраической операции и образованной сложной функции.
7) Характеристики функции.
Опр . функция y=f(x) именуется четной, в случае, если для х в собственности Х f(-x)= f(x)
Нечетной именуют функцию в случае, если для x в собственности Х, f(x) = -f(x)
Ни четная ни нечетная именуется функция обратного вида.
Возрастающую и убывающую функцию именуют монотонной.
Опр. Функция y=f(x) ограниченная в случае, если существует (с больше 0) что для х пренадлежащего Х выполняется модуль f(x) больше либо равняется С.
Опр. Функция y=f(x) периодическая, в случае, если Т не равен 0, в случае, если существует Т не равное 0, что для любых х принадлежащих Х равняется f(x+n)= f(x).
 Предел функции в точке.
Предел функции в точке.
Опр. Число а именуется пределом функции f(x) в точке х нулевае, в случае, если f(x) определеа окресностью Х нулевое и для любого малого числа сигма больше 0, найдется число дельта больше 0 , то что для Х не равного Хнулевому , еслм модуль Х-Хнулевое меньше дельта, либо модуль f(x)-a меньше Сигма.
Опр. Пускай f(x) опрделена на промежутке (Хнулевое –дельта, до Хнулевого) где дельта больше 0, тогда число а именуется пределом f(x) слева от точки Хнулевое, в случае, если для Сигма больше 0 существует дельта больше 0, что для всех х принадлежащих( Хнулевому – дельта, до Хнулегого) выполняется (f((x)=a) больше Сигма.
Опр. F(x) выяснен на промежутке ( Хнулевого; Хнулевое +дельта), дальта больше 0, тогда а2 придел f(x) справа точкт Хнулевого, в случае, если Х( Хнулевое; Хнулевое +дельта)равносильно (f(x) –a2) меньше Сигма .
Теорема о пределах.
9) Теоремы о пределах.
10) Первый и второй превосходные пределы.
Первый превосходный предел: Существует предел Х стремящийся к 0 синус Х дроблённый на Х , в случае, если предел х стремящийся к 0 х дроблённый на синус Х =1.
Второй превосходный предел: Предел семь дней стремящ. К бесконечности ( 1+ 1 деленая на Х) в степени Х =е , либо предел Х стемится к бесконечности( 1+U) в степени Х =е.
11) Непрерывность функции.
Опр. F(x) постоянна в точке Хнулевое , в случае, если :
1 существует значение функции
2 существует предел функции
3 предел функции в точке равен её значению.
Опр. Точка в которой нарушено хотя бы одно условие непрерывности именуется точкой разрыва.
Опр. Точка Хнулевое именуется точкой разрыва 1-го рода, в случае, если существует конечные пределы функции в данной точке слева и справа, но они не равны между собой, или не равны значению функции в точке Хнулевое.
Опр. Точка разрыва 1-го рода именуется устраненным разрывом, в случае, если существует и равные пределы слева и справа, но f(x) либо не выяснена в точке Хнулевое либо не равна значению функции в данной точке.
Опр. Точка а именуется точкой разрыва 2-го рода f(семь дней) в случае, если в данной точке функция не имеет по крайней мере одного из односторонних пределов либо хотя бы один из односторонних пределов нескончаем.
Функция не прерывна постоянна на промежутке Хбольшое , если она постоянна в каждой точке этого промежутка.
12) Свойства функций непрерывности в точке.
1. В случае, если f(x) и g(x) постоянны в точке Хнулевое, то f(x) +_ g(x); f(x)* g(x)
f(x) дроблённая на g(x)( при g(x) не =0) кроме этого постоянна в точке Хнулевое.
2. f(x) постоянна в точке Хнулевое и f(x) больше 0, тогда существует окресность в точке Хнулевое в которой f(x) больше 0.
3. f(u) постоянна в точке Uнулевое, и U=фи(х) постоянна в точке Хнулевое в случае, если f(фи(x))- постоянна в точке Хнулевое т.е. для постоянной ф-ции предел х стремящийся к Хнулевому f(фи(х))=f lim х стремящийся к Хнулевому фи(х).
13) Производная в точке.
Опр. Производная функции f(x) в точке Хнулевое именуется пределом отношения прирощения функции в данной точке к прирощению довода при треугольник Х пытается к 0.
Опр. Функция именуется дифференцируемой в точке Хнулевое , в случае, если в данной точке оно имеет конечную производную.
Теорема о дифференцируемости и связи непрерывности.
В случае, если f(x) диф. В точке Хнулевое , то f(x) постоянна в данной точке.
14) Правила дифференцирования.
Пускай U и V диф. В точке Хнулевое.
1 ( c+u) производная = c *u производная
2 (u+_v) проиводная = производная U + _ производная V
3 как простые производные умнодения
4 как в большинстве случаев производные деления
5 в случае, если y(u) диф. в точ. Хнулевое U=U(Хнулевое) то сложная функция производная y(x нулевое) = производ. y(u нулевое) * производная U(Хнулевое)
6 в случае, если производная y(x) не=0, то обратная функция производная Х(у)= 1 деланая на производную направляться(x).
15) Теоремы о дифференцируемых функциях.
Теорема Ферма
В случае, если f(х) диф. На Хбольшое и достигает громаднейшего либо мельчайшего значения в т. Хнулевое в собственности Хбольшому, то f(Хнулевое)=0
Теорема Ролля
1. F(x) – постоянна на отрезке квадрат. Скобки а;b
2. F(x) диф. На промежутке (а;b)
3. F(a) =f(b) тогда внетри отрезка существует по крайней мере одна точка
Сигма(констанат) в собственности (a;b) такая что f(сигма)=0
Теорема Лангранжа
1. F(x) постоянна на отрезке a;b
2. F(x) диф. На интеграле (a;b)
Тогда в отрезка существует по крайней мере одна т. Сигма в собственности (a;b) такая что производная f(сигма)= f(a)-f(b) дроблённые на b-a.
16) Дифференциал функции.
Пускай f(x) диф. в т. Хнулевое тогда треугольникУ =f(Хнулевое) * треугольник Х + альфа, где альфа бесконечно малое , более большого порядка чем треуг.Х при треуг.Х пытается к 0
Опр. Дифференциал функции в точке именуется произведением производной функции в точке на прирощение свободной переменной. d(y)= производная f(x)* треугольникХ
Геометрический суть- величина деф. функции равняется прирощению ординаты касательной к графику в точке (Хнулевое; Унулекой) при переходе к точке ( Хнулевое +треуг.Х равносильно f(Хнулеевое + треуг.Х)
Правила нахождения дифференциала
1. dc = 0; c-const
2. d(c*f(x)) в степени Х= c*df(x)
3. d(x в степени n)=n*(x в степени n-1)
4. d(U +_V)= dU+_dV
5. d(U*V)=dU*V+U*dV
6. d(U:V)= dU*V-U*dV : V в квадрате
7. d(y(u( Хнулевое))=производная y(U нулевое) *dU(Хнулевое)
17) Монотонность функции.
Моното?нная фу?нкция — это функция, приращение которой не меняет символа, другими словами или в любой момент неотрицательное, или в любой момент неположительное.
Нужное условие монотонности
В случае, если f(x) диф. На Хбольшое и возростает(убывает), то производная функции f(направляться) больше либо равняется 0 на Хбольшое.
Экстремумы функции.
Опр. Хнулевое именуется т. Максимума функции, в случае, если существует дельта больше 0, что для любых Х равносильно 0 меньше модуль Х-Хнулевое меньше дельта правильно f( Хнулевое) меньше f(x).
Опр. Хнулевое именуют т. Минимума функции в случае, если дельта меньше 0, что для любых Х равносильно 0 больше модуль Х-Хнулевое больше дельта правильно f(Хнулевое) меньша f(x).
Теорема (нужное условие локального экстремума)
В случае, если f(x) диф. И имеет экстремумы в точке Хнулевое , то её производная в данной точке равняется 0, или не существует.
Точки в которых производная =0 либо не существует именуется критическими
Теорема (достаточное условие локального экстремума)
Пускай f(x) диф. в некоей октесности Хнулевое, в случае, если при переходе через эту точку производная функции меняет символ с «+» на «-» либо напротив, то Хнулевое точка максимума либо минимума( max, min)
Второе достаточное условие
Пускай f(x) два раза диф. в некоей окресности Хнулевое, в случае, если производная f(x) =0 а вторая производная f(x) не=0 то Хнулевое т. Максимума , в случае, если вторая производная f(x) меньше 0, и Хнулевое минимум в случае, если вторая прпоризводная f(x) больше 0.
18) вогнутость и Выпуклость функции
Опр. Функция именуется выпуклой(вогнутой) на промежутке, в случае, если на этом промежутке график функции расположен не выше(не ниже) касательной совершённой в любой точке этого промежутка.
Точки перегиба
Опр. Точка, в которой выпуклость выпуклость меняестся на вогнутость и напротив именуется точкой перегиба.
Теорема( нужное достаточное условие существования точки перегиба).
Пускай y=f(x) имеет постоянную вторую производную на промежутке(a;b) и т.Хулевое из(a;b)- т. перегиба графика функции, то 2-я производная функции данной точки =0 ( 2-я производная f(x)=0)
Теорема (достаточное условие существования точке перегиба).
Пускай y=f(x) имеет постоянную вторую производную f(x) на (a;b), в случае, если при переходе черех т. Хнулевое y= вторая производная f(x) меняет символ, то т. М (Хнулевое; f(Хнулевое)) есть т. перегиба графика функции.
19) Асимптоты
Опр. Прямая именуется асимптотой кривой в случае, если расстояние от точки кривой до данной прямой пытается к 0 при неограниченном удалении точки на протяжении кривой от начала координат.
Вертикальные и горизонтальные асимптоты
Прямая х=а, есть вертикальной асимптотой линии y=f(x) в случае, если один либо оба односторонних предала при х стремящимся к а нескончаемы.
Невертикальная асимптота
Прямая y=kx+b есть невертикальной асимптотой линии y=f(x) в случае, если существуют конечные приделы.
Горизонтальная асимптота это в случае, если k=0.
Правило Лопиталя
Пускай функция f(x) и g(x) диф. некоей окрестности т. Хнулевое и y= производная g(x) не =0 в данной окрестности, в случае, если предел Х стреммящийся к Хнулевому f(x)= пределу Х стремящийся к Хнулевому g(x)=0 либо оба эти предела равны бесконечности, то для всех точек данной окресности выполняется равенство:
Предел Х= Хнулевому f(x) : g(x)= lim x= Хнулеваму f’(x): g’(x)
20)
21)
22)
23)
24)
25)
Тория возможности
Точные это те события , каковые непременно случатся при осуществлении комплекса условий S
Случайные именуют события каковые может или случиться или не случиться при осуществлении комплекса условий S
Неосуществимыми именуются те события , каковые заведомо известно не произ-ойдет при осуществлении комплекса условий.
Виды случайных событий
События именуют несовместными, в случае, если появление одного из них, исключает появление вторых событий в одном и том же опробовании.
Пример. Кинута монета. Появление «герба» исключает появление надписи. События «показался герб» и «показалась надпись» — несовместные.
Пара событий образуют полную группу, в случае, если в следствии опробования покажется хотя бы одно из них. Др. словами, появление хотя бы одного из событий полной группы имеется точное событие. В частности, в случае, если события, образующие полную группу, попарно несовместны, то в следствии опробования покажется одно и лишь одно из этих событий. Данный частный случай воображает громаднейший интерес для нас.
Пример. Стрелок произвел выстрел по цели. Непременно случится одно из событий: попадание, промах. Эти два несовместных события образуют полную группу.
События именуют равновозможными, в случае, если имеется основания вычислять, что ни одно из них не есть более вероятным, чем второе.
Пример. Появление того либо иного числа очков на кинутой игральной кости – равновозможные события. Вправду, предполагается, что игральная кость изготовлена из однородного материала, имеет форму верного многогранника и наличие очков не влияет на выпадение любой грани.
27) Элементарные финалы опробований
Хорошее определение возможности
Любой из вероятных результатов опробования именуют элементарным событием либо элементарным финалом.
Класическое определения связано с понятием помогающего финала.
Свойство возможности
1) Возможность точного события =1
2) Возможность неосуществимого события=0
3) Возможность случайного события – это число 0 меньше либо равен Р(А) меньше либо равняется 1
Формулы комбинаторики
Перестановками именуется комбинации складывающиеся из одной и той же совокупности n разных элементов и оличающиеся лишь порядком их размещения.
Размещениями именуются комбинации по m элементов соствленных из n разных элементов или их порядком.
Сочетаниями именуется комбинации которые содержат по m элементов состоящих их n разных элементов и отличающихся хотя бы одним элементом.