Министерство образования и науки РФ
ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ ВЫСОКИХ РАЗРАБОТОК
Курсовая работа
Технологии корреляционно-регрессивного
анализа и их практическое
применение.
Выполнила: Богаченко К.С.
2 курс 5несколько
Начальник: Остроух Е.Н.
г. Ростов-на-Дону
Содержание
I. Теоретическая часть
1. Технологии корреляционно-регрессивного анализа……………………… 3
2. Этапы корреляционно-регрессивного анализа…………………………… 5
- Нулевой этап……………………………………………………….5
- Первый этап (Корреляционный анализ)…………………………5
- Второй этап …………………………………………………………5
- Третий этап……………………………………………………… ..6
- Четвертый этап……………………………………………………..7
3. Главные способы поиска наилучшего ответа………………………… 8
II. Практическая часть
1. Симплекс способ………………………………………………10
2. Транспортная задача…………………………………………14
I. Теоретическая часть
Технологии корреляционно-регрессивного анализа
Экономические эти практически в любое время представлены в виде таблиц. Числовые данные в таблицах в большинстве случаев имеют между собой явные (узнаваемые) либо неявные (скрытые) связи.
очевидно связаны показатели, каковые взяты способом прямого счёта, т.е. вычислены по заблаговременно известным формулам. К примеру, проценты исполнения на уровне, удельные веса, отклонения в сумме, отклонения в процентах, скорость увеличения, темпы прироста, индексы и т.д. Связи второго типа заблаговременно малоизвестны, исходя из этого при помощи наблюдений стараются распознать скрытые зависимости и выразить их в виде формул, МС, математически смоделировать явления либо процессы. Для этого помогает корреляционно-регрессивный анализ.
Математические модели строим и используем для 3-х целей:
1. для объяснения;
2. для предсказания;
3. для управления.
Пользуясь способами корреляционно-регрессивного анализа, возможно измерить густоту связей показателей посредством коэффициента корреляции. Наряду с этим связи смогут быть сильными, не сильный, умеренными, разными по направлению — прямые и обратные. В случае, если связи значительны, то их математическое выражение изменяется в виде регрессивной модели с оценкой систематической значимости модели. Значимое уравнение употребляется для прогнозирования изучаемого явления либо показателя.
Корреляционно-регрессивный анализ связи между переменными показателями как один комплект переменных(Х), может влиять на другой комплект (У).
Пример 1.
Способами, изучающими потери продвижения и пути товаров в пути, возможно проверить предположение о том, что число консервных банок, сломанных при перевозке в вагонах, зависит от скорости вагонов при толчках. Это даёт возможность при расфасовки товаров и перепроектировки упаковки поменять методы доставки, и погасить естественную убыль. Собраны информацию о скорости 13 вагонов (свободные переменные Х) и количество сломанных банок в каждом из них (зависимые переменные У). В случае, если при обработке этих данных выявится сильная связь между Х и У, то нужно будет выстроить её механическую модель для прогнозирования утрат при перевозке и нормировании товаров.
Пример 2.
Хиромантия говорит, что эти «линии судьбы» на левой ладони человека связана с длительностью его жизни. Способом прямого наблюдения собранны информацию об подлинном возрасте 50-ти погибших согласно данным «линии судьбы», дабы посредством корреляционно-регрессивного анализа измерить силу связи и отыскать научное объяснение хиромантии.
Пример 3.
Управляющий операцией одной из компаний принял последовательность ответов по мероприятиям на стадионе с учётом возможной их посещаемости – какое количество в каждом случае необходимо открыть киосков и какое количество работников позвать на работу. Оказалось, что одна из основных свободных переменных, которую возможно встроить в прогнозируемую модель, типа множественной линейной регрессивной модели – это число билетов реализованных на стадионе к моменту, в то время, когда до игры остаётся 24 часа.
Пример 4.
Увидено, что количество продаж, зависит от площади предприятия. Отыскать уравнение данной зависимости, дабы по известной площади универмага (Х) возможно было реализовать неспециализированные продажи в нём (У). Само собой разумеется, принципиально важно иметь информацию о типе предприятия, т.к. сообщение возможно неодинакова для больших и небольших фирм.
Итак, таковой подход употребляется в маркетинге, торговле, медицине. Взяв знание о скрытых связях, возможно улучшить аналитическую помощь принятия ответов и повысить их обоснованность. В маркетинге активно используется, как однофакторные, так и множественные регрессивные модели. Корреляционно-регрессивный анализ – один из основных способов в маркетинге, наровне с расчётами, и математическим и графическим моделированием трендов (тенденции).
Этапы корреляционно-регрессивного анализа
Нулевой этап.
Цель—сбор данных. Эти должны быть замечаемы, т.е. взяты в следствии замера, а не расчёта. Наблюдение направляться спланировать. какое количество нужно данных чтобы получить хорошее уравнение? Их должно быть в 4-6 раза больше, чем число факторов, влияние которых необходимо выразить математически (по вторым оценкам в 7-8 раза больше). Это обеспечит действенное погашение случайных отклонений от закономерного характера связей показателя.
Первый этап.
Корреляционный анализ.
Цель –выяснить темперамент связи (прямая, обратная) и силу связи (отсутствие связи; сообщение не сильный, умеренная, сильная либо малая). степень и Характер выраженности связей определяется коэффициентом корреляции, что употребляется для отбора значительных факторов, и для последовательности расчёта и планирования эффективности параметра регрессивных уравнений. Присутствие одного фактора вычисляется коэффициентом корреляции, а при наличии нескольких факторов строится корреляционная матрица, из которой выявляется 2 вида связи:
1. сообщение зависимой переменной;
2. связь между свободными переменными.
Выше распознанные факторы, вправду воздействуют на последующую зависимую переменную, и нужно выбрать (ранжировать) их по убыванию связи; во-вторых, минимизировать число факторов модели, исключив часть факторов, каковые функционально связаны с другими факторами (связь свободных переменных между собой).
Второй этап.
Это построения расчета и этап параметра регрессивных моделей. Он содержится в том, дабы отыскать самая точную меру обнаружения связи. Эту меру обобщенно высказываем математической моделью множественной регрессивной зависимости:
у = а0 + в1+х1+х2*2+…вnхn
ВеличинаУ – отклик, Х1,Х2 …Хn –факторы, а0-const, В — коэффициент регрессии. На втором этапе корреляционно-регрессивного анализа по окончании выбора коэффициентов, переход к третьему этапу— интеллектуальному, для которого практически все сведенья по оценке значимости уравнения подготавливает ЭВМ.
Третий этап.
На 3-ем этапе вычисляется величина (параметр) значимости, т.е. пригодность постулированной модели для анализа (разработки) в целях предсказания значений отклика. Наряду с этим программа рассчитывает по модели теоретическое значение для ранее замечаемых значений зависимой величины и вычисляет отклонение теоретических знаний от замечаемых значений. На базе этого программа сооружает последовательность графиков, а также график подборки (он иллюстрирует как отлично подобраны линии регрессии к замечаемым данным), график элементов.
В остатках не должно наблюдаться закономерности, т.е. коррекция с каким-либо значением на этом этапе только ключевую роль играется коэффициент детерминации.
MF- критерий значимости регрессии. R Squared (семь дней2)—коэффициент детерминации – квадрат множественности коэффициента корреляции между замечаемыми значениями. У и его теоретическое значение, вычисленное на базе модели с определённым комплектом факторов. Коэффициент детерминации измеряет реальность модели. Он может принимать значение от 0 до 1. Эта величина особенно нужна для сравнения последовательности разных выбора и моделей наилучшей из них.
R2 – для вариации прогнозируемой (теоретической) величины у довольно замечаемых значений У1, растолкованном за счёт включенных в модель факторов. Отлично, в случае, если R2 ?80%. Остальные для замечаемых значений У зависят от вторых, не участвовавших в модели факторов. Задача последователя обнаружить факторы, увеличивающие R2 и давать объяснения вариации прогнозов, для получения идеального уравнения. Дубликаты данных следует удалять из исходной таблицы до начала расчёта регрессии.
R2= 1 только при полном согласии экспериментальных (замечаемых) и теоретических (расчётных) данных, т.е. в то время, когда теоретическое значение совершенно верно сходится с замечаемым.
В EXCEL – выполняется F-критерий значимости регрессии для уравнения в целом. Это вычислено по замечаемым данным значениям.FP (F—расчетный, замечаемый) направляться сравнивать соответствующим критическим значением FK(F—критический, табличный).FK выбирается из публикуемых статистических таблиц на заданном уровне (на том, на котором вписывались периметры моделей, к примеру, 95%). В случае, если замечаемое значение FP окажется меньше критического FK, то уравнение нельзя решить, т.е. не отвергнуть нуль – догадка относительной значимости всех коэффициентов регрессии постулируемой модели, т.е. коэффициент фактически равен нулю.
Замечаемое значение F должно не просто превышать выбранную процентную точку F—распределения, а превосходить её в 4 раза.
К примеру, пускай F (10; 20; 0,95)=2,35, тогда замечаемое значение F-Х отношения должно превосходить 9,4, чтобы возможно было расценивать полученное уравнение как удовлетворительную модель для предсказания.
Четвертый этап.
На 4-ом этапе корреляционно-регрессивного исследованияполученную модель систематического значения используют для прогнозирования (предсказания), управления либо объяснения.
Главные способы поиска наилучшего ответа
Существует пара алгоритмов и способов выбора наилучшего уравнения регрессии:
1. Способ всех вероятных регрессий,
2. Способ выбора «наилучшего подмножества» предикторов
3. Способ исключения
4. Шаговый регрессионный способ.
5. Гребневая регрессия.
6. Пресс.
7. Регрессия на основных компонентах.
8. Регрессия на собственных значениях.
9. Ступенчатый регрессионный способ.
10. Устойчивая регрессия.
11. Другие, более ранние способы (способ деления пополам, способ складного ножа и т.д.).
Техногенный и шаговый способы самый действенны при применении ЭВМ.
Способу исключения следуют не все, а лишь наилучшие регрессионные уравнения, в чём и состоит его экономичность. На первой стадии в рассчитываемые уравнения включают все свободные переменные. После этого, разглядывают корреляционную матрицу, находят свободную переменную, самую не сильный (по модулю) сообщение с зависимой (т.е. с мельчайшим по модулю значением коэффициента корреляции) и исключают её из уравнения. Заново производят перерасмотрение уравнение с меньшим числом свободных переменных. В случае, если если сравнивать с прошлым расчётом значимость уравнения в целом (FP) и коэффициент детерминации(R2) повышен, то исключение сделано правильно. После этого отыскивают в корреляционной матрице следующую переменную с мельчайшим значением коэффициента корреляции, поступают подобно. Исключение свободных переменных (по одной) и пересчет уравнений продолжают до тех пор, пока не найдут доли значимости вариации и снижение уравнения(R2) если сравнивать с последними предшествующими расчётами. Это является сигналом нецелесообразности последнего исключения.
Шаговый способ—действует в противоположном направлении, начиная с однофакторной модели. Наряду с этим ориентируются на эти корреляционной матрицы, т.е. на первом шаге расчёта в уравнении включают не все факторы, а лишь один с громаднейшим по модулю значением коэффициента корреляции между свободной и зависимой переменными значениями. На каждом следующем шаге из оставшихся, не включенными в уравнение свободных переменных, в прошлую модель додают лишь одну свободную переменную самая связанную с зависимой, и заново пересчитывают все параметры регрессии. По окончании пересчёта сравнивают полученные оценки нового уравнения с оценками прошлого шага. Так длится до тех пор, пока не возьмут наилучшее уравнение с громаднейшим расчётным значением F и R2 .
При помощи множественного регрессивного анализа средствами EXCEL возможно отслеживать очерёдность для каждого шага: номер шага, комплект свободных переменных, вид уравнения, новые оценочные эти, коэффициент (F—расчётный и F—критический) и т.д.
| № А Г А | Количество факторов | Участвующие свободные переменные | Вид взятой модели | FP | FK | R2 | Выводы о роли включенного либо исключенного фактора, о значимости модели, отборе лучшей модели |
II. Практическая часть
1. Симплекс способ
Постановка задачи
Компания создаёт две модели А и В сборных книжных полок. Их производство ограничено наличием сырья отличных досок и временем машинной обработки. Для каждого изделия А требуется 3 м2 досок, а для изделия В- 4 м2. Компания может получить от своих поставщиков до 1700 м2 досок в неделю. На каждое изделие А требуется 12 мин. машинного времени, а на изделие В – 30. В неделю возможно применять 160 часов машинного времени. В случае, если каждое изделие модели А приносит 2$ прибыли, а изделие В – 4$ прибыли, сколько изделий каждой модели компании нужно производить в неделю?
Цель — разработать замысел производства требуемых изделий, снабжающий большую прибыль от их реализации, свести данную задачу к задаче линейного программирования, решить её симплекс — способом.
Построение математической модели
| Целевая функция | ||||
| Имя | Формула | |||
| F | ||||
| A | B | Сумма | ||
| Ресурсы | ||||
| Время | 1/5 | 1/2 | ||
| Прибыль |
Построение математической модели осуществляется в три этапа :
1. Определение переменных, для которых будет составляться математическая модель.
Так как требуется выяснить замысел производства изделий А и В, то переменными модели будут:
x1 — количество производства изделия А, в единицах;
x2 — количество производства изделия В, в единицах.
2. Формирование целевой функции.
Так как прибыль от реализации единицы готовых изделий А и В известна, то неспециализированный доход от их реализации образовывает 2×1 + 4×2 ($). Обозначив неспециализированный доход через F, возможно дать следующую математическую формулировку целевой функции: выяснить допустимые значения переменных x1 и x2 , максимизирующих целевую функцию F = 2×1 + 4×2 .
3. Формирование совокупности ограничений.
При определении замысла производства продукции должны быть учтены ограничения на ресурсы и время для изготовления всех изделий. Это ведет к следующим двум ограничениям : 3×1 + 4×2 ? 1700 ; 1/5×1 + 1/2×2 ? 160.
Так как количества производства продукции не смогут принимать отрицательные значения, то появляются ограничения неотрицательности: x1, x2 ³ 0 .
Так, математическая модель задачи представлена в виде: выяснить замысел x1, x2, снабжающий большое значение функции при наличии ограничений:
при:
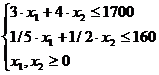
Приведем задачу к каноническому виду и добавим переменные:
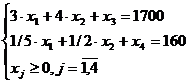
Определим начальный опорный замысел:
L1=0
Оформим этот этап задачи в виде симплекс-таблицы.
Первая симплекс-таблица.
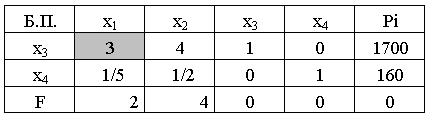
Рис.1.1.Первая симплекс-таблица
Опорный замысел есть оптимальным, в случае, если для задачи максимизации все его оценки отрицательны, т.е. в последней строчке все элементы неположительные либо нулевые. В этом случае не есть оптимальным, значит, критерий возможно улучшить процесс.
Берем из последней строчка хороший элемент и просматриваем над ним столбец (элементы должны быть хорошими). Используем соотношение для j-го столбца, выбираем элемент, при котором это выражение минимально. Знаменатель самого минимального элемента именуем ведущим. Осуществим, как продемонстрировано на рис. 1.1, перевод:x1 — в базис, x3 — в переменные.
Пересчитаем элементы исходной таблицы по следующему правилу:
1) Числа, стоящие в одной строке с ведущим элементом, делим на данный элемент;
2) Все остальные элементы пересчитываем по правилу четырехугольника.
Вторая симплекс-таблица.

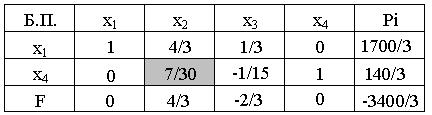
Рис.1.2.Вторая симплекс-таблица
L2=3400/3
Опорный замысел не есть оптимальным. Выбираем ведущий элемент и пересчитываем таблицу.
Третья симплекс-таблица.
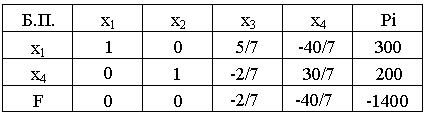
Рис.1.3.Третья симплекс-таблица
Опорный замысел есть оптимальным, т.к. все его оценки отрицательны (рис. 1.3), т.е. в последней строчке все элементы неположительные либо нулевые.
L3=1400
Ответ данной задачи в Ms Excel
Для решения задачи нужно, дабы на компьютере был установлен программный продукт Микрософт Excel версии 1997-2003.
Нужно произвести установку надстройки ”Поиск ответа”. Для этого направляться выполнить следующее воздействие: из пункта меню выбрать Сервис/Надстройки, в открывшемся окне отметить галочкой “Поиск ответа” и надавить ОК (Рис. 1.4).
Рис. 1.4. Установка надстройки ”Поиск ответа”
Для решения задачи нужно ввести входные эти (рис. 1.5):
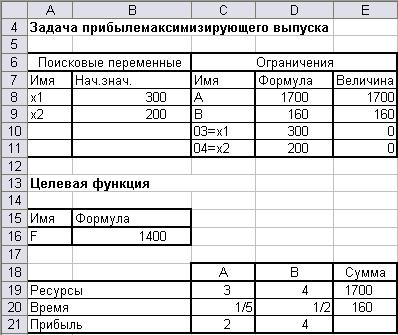
Рис. 1.5. Входные эти
Установив курсор на ячейке В16, выполнить действия Сервис/Поиск ответа/Выполнить/Сохранить отысканные ответы (Рис. 1.6). Затем в ячейку В16 будет выведен ответ. В ячейках В8,B9 машинально строится оптимальный замысел.
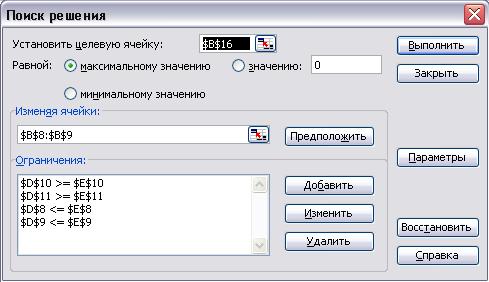
Рис. 1.6. Поиск ответа
2. Транспортная задача
Транспортная задача содержится в нахождении для того чтобы замысла поставок, при котором его цена минимальна.
Нужно решить транспортную задачу, с входными данными. Условия задачи задаются в виде таблицы:
| Потребители | Поставщики | |||
| В1 | В2 | Вn | ||
| C11 X11 | C12 X12 | … | C1n X1n | А1 |
| C21 X21 | C22 X22 | … | C2n X2n | А2 |
| … | … | … | … | … |
| b1 | b2 | … | bn |
Матрица (cij)m*n именуется матрицей тарифов. Замыслом транспортной задачи именуется матрица х=(xij)m*n, где каждое число обозначает количество единиц груза, которое нужно доставить из i–го пункта отправления в j–й пункт назначения.
Ответ транспортной задачи начинается с нахождения опорного замысла. Для этого существуют разные методы. К примеру, метод “северо-западного угла”, способ минимального элемента. Клетки таблицы, в которых стоят ненулевые перевозки, являются базовыми. Их число должно равняться m + n — 1.
Для решения транспортной задачи употребляется способ потенциалов. Мысль способа потенциалов для ответа транспортной задачи сводиться к следующему. Представим себе что любой из пунктов отправления Ai вносит за перевозку единицы груза (всё ровно куда) какую-то сумму ai ; со своей стороны любой из пунктов назначения Bj кроме этого вносит за перевозку груза (куда угодно) сумму bj . Эти платежи передаются некоему третьему лицу (“перевозчику“). Обозначим ai + bj = ci,j ( i=1..m ;j=1..n) и будем именовать величину ci,j “псевдостоимостью” перевозки единицы груза из Ai в Bj . Увидим, что платежи ai и bj не обязательно должны быть хорошими; нельзя исключать, что “перевозчик” сам платит тому либо второму пункту какую-то премию за перевозку. Кроме этого нужно подчернуть, что суммарная псевдостоимость любого допустимого замысла перевозок при заданных платежах (ai и bj ) одинаковая и от замысла к замыслу не изменяется.
До сих пор мы никак не связывали платежи (ai и bj ) и псевдостоимости ci,j с подлинными ценами перевозок C i,j. Сейчас мы установим между ними сообщение. Предположим, что замысел (xi,j) невырожденный (число базовых клеток в таблице перевозок ровно (m + n -1). Для всех этих клеток xi,j 0. Определим платежи (ai и bj ) так, дабы во всех базовых клетках псевдостоимости были ровны ценам:
ci,j = ai + bj = сi,j , при xi,j 0.
Что касается свободных клеток (где xi,j = 0), то в них соотношение между псевдостоимостями и ценами возможно какое угодно.
Оказывается соотношение между псевдостоимостями и ценами в свободных клетках показывает, есть ли замысел оптимальным либо же он бывает улучшен. Существует особая теорема: В случае, если для всех базовых клеток замысла (xi,j 0)
ai + bj = ci,j= сi,j ,
а для всех свободных клеток ( xi,j =0)
ai + bj = ci,j? сi,j ,
то замысел есть оптимальным и никакими методами улучшен быть не имеет возможности.
Задача (входные эти представлены в виде таблицы )
| Потребители | Поставщики | ||||
| В1 | В2 | В3 | В4 | В5 | |
Находим количество единиц груза способом северо-западного угла.
| Потребители | Поставщики | ||||
| В1 | В2 | В3 | В4 | В5 | |
L1=395
Посредством способов потенциалов определяем, что полученный замысел не есть оптимальным. Пересчитываем таблицу, для этого строим цикл.
| Потребители | Поставщики | ||||
| В1 | В2 | В3 | В4 | В5 | |
 __ 5 __ 5 |
+ 6 | ||||
| + 23 | __ 7 | ||||
Вторая таблица транспортной задачи
| Потребители | Поставщики | ||||
| В1 | В2 | В3 | В4 | В5 | |
L2=380
Опорный замысел не есть оптимальным, пересчитываем таблицу, строя цикл.
| Потребители | Поставщики | ||||
| В1 | В2 | В3 | В4 | В5 | |
 + 5 + 5 |
__ 3 | ||||
| __ 23 | + 8 | ||||
| __ 1 | + 5 | ||||
Третья таблица транспортной задачи.
| Потребители | Поставщики | ||||
| В1 | В2 | В3 | В4 | В5 | |
L3=335
Полученный опорный замысел есть оптимальным. И никакими методами улучшен быть не имеет возможности.
Ответ транспортной задачи в Ms Excel. Для решения задачи нужно ввести входные эти(рис.2.1).
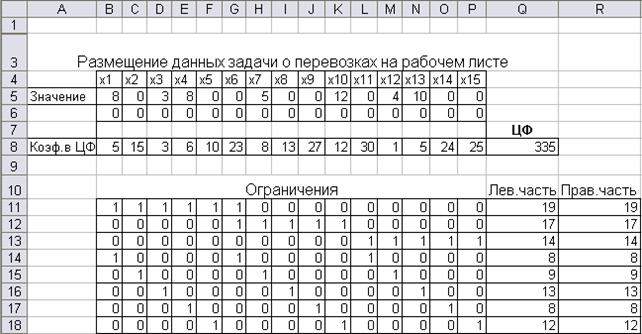
Рис. 2.1.Входные эти
Установив курсор на ячейке Q8, выполнить действия Сервис/Поиск ответа/Выполнить/Сохранить отысканные ответы (Рис. 2.2). Затем в ячейку Q8 будет выведен ответ. В ячейках В5-E5 машинально строится оптимальный замысел.
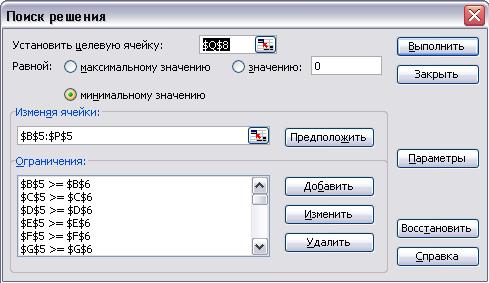
Рис. 2.2. Поиск ответа