ТЕМА 2.1. ЗАДАЧИ. ПРИВОДЯЩИЕ К ВЫЧИСЛЕНИЮ ИНТЕГРАЛОВ
Определенный интеграл
Определённым интегралом от постоянной функции f(x) на конечном отрезке [a, b] (где ) именуется приращение какой-нибудь её первообразной на этом отрезке. (По большому счету, познание заметно облегчится, в случае, если повторить тему неизвестного интеграла) Наряду с этим употребляется запись
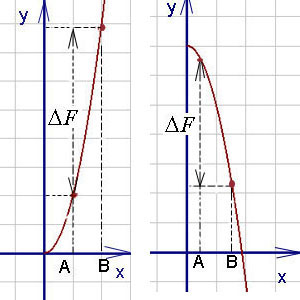
Как видно на графиках внизу (приращение первообразной функции обозначено ), определённый интеграл возможно как хорошим, так и отрицательным числом (Вычисляется как разность между значением первообразной в верхнем пределе и её же значением в нижнем пределе, т. е. как F(b) — F(a)).
Числа a и b именуются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.
Так, в случае, если F(x) – какая-нибудь первообразная функция для f(x), то, в соответствии с определению,
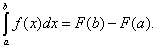
Равенство (38) именуется формулой Ньютона-Лейбница. Разность F(b) – F(a) коротко записывают так:
Исходя из этого формулу Ньютона-Лейбница будем записывать и без того:
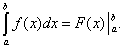
Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции забрана при его вычислении. Пускай F(x) и Ф(х) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х) = F(x) + C. Исходя из этого
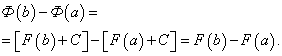
Тем самым установлено, что на отрезке [a, b] приращения всех первообразных функции f(x) совпадают.
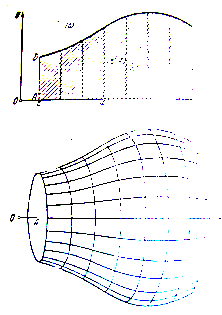
Задача о вычислении площади произвольной криволинейной трапеции.
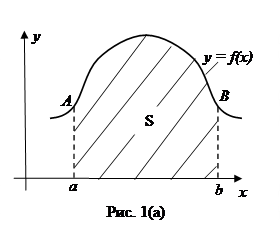Разглядим рис. 1(а), где – некая постоянная на функция.
Заштрихованная на этом рисунке фигура именуется криволинейной трапецией. А S — площадь данной трапеции. Поставим, за Лейбницем и Ньютоном, задачу: вывести формулу для площади S данной трапеции при заданных a, b и f(x).
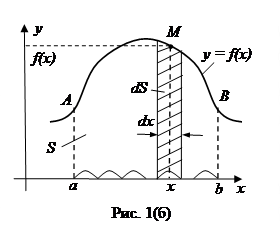
Ответ. Разобьем в мыслях отрезок оси ох (основание трапеции) на бесконечно малые участки, как это продемонстрировано на рис. 1(б). Для простоты будем вычислять их однообразными по длине. Эту бесконечно малую длину каждого участка обозначим знаком dx. В случае, если через финиши этих участков совершить вертикальные прямые, то вся криволинейная трапеция разобьется на вечно много вечно узких вертикальных полос шириной dx. Разглядим одну из таких полос (любую), и отыщем ее площадь dS (см. рис. 1(б)).
Заберём в основании полосы некую произвольную точку х. Так как полоса вечно узкая (другими словами она представляет собой вертикальную нить), то х – это точка, являющаяся основанием данной нити. В соответствии с рис. 1(б), площадь dS разглядываемой полосы (нити) возможно отыскать, умножив ее высоту f(x) на ширину dx. Другими словами
dS = f(x)dx (1)
Но, таковой была бы площадь dS полосы, если бы полоса была прямоугольником с основанием dx и высотой f(x). Но отечественная полоса имеет сверху криволинейную границу, а f(x) — высота, на которой находится только одна из точек (точка М) данной границы. Все остальные точки указанной верхней границы полосы находятся, по большому счету говоря, на другой, хоть и близкой к f(x), высоте. Так что формула (1) для площади каждой из полос, на каковые мы в мыслях разбили криволинейную трапецию, не правильная, а приближенная. Но разумеется, чем уже полоса, тем правильнее формула для ее площади dS. А так как отечественная полоса (как и все остальные) не просто узкая, а вечно узкая, то мы вправе вычислять формулу (1) правильной.
Складывая сейчас площади dS всех вертикальных полос, отыщем, причем совершенно верно, и всю площадь S криволинейной трапеции:
(2)
Эта сумма необыкновенная: слагаемые в ней бесконечно малые, а число слагаемых вечно громадно (S — суммабесконечно солидного числа бесконечно малых слагаемых). Данной сумме Лейбниц дал особое обозначение.
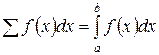(3)
и назвал ее определенным интегралом от функции f(x). Тут f(направляться)– подынтегральная функция; f(x)dx — подынтегральное выражение; x – переменная интегрирования; a и b — пределы интегрирования (нижний и верхний).
Итак, в соответствии с (2) и (3),
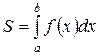(4)
— площадь криволинейной трапеции, изображенной на рис. 1(а).
Протяженность дуги
Для начала введём понятия о спрямляемой дуге и её длины.
Разглядим на плоскости кривую AB , заданную параметрическими уравнениями , , ( ), (8)
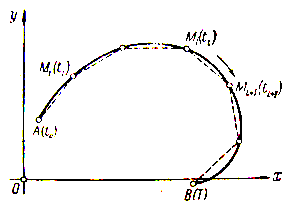
где функции и предполагаются постоянными. Будем вычислять, что точка A отвечает значению , а точка Bзначению . Наряду с этим пускай кратных точек на кривой нет, так что разным значениям параметра отвечают и разные точки кривой.
В случае, если вычислять точки кривой (чертёж 11) расположенными в порядке возрастания параметра (т.е. из двух точек ту принимать за следующую, которая отвечает большему значению параметра), то этим на кривой создаётся определённое направление (чертёж 11). Заберём сейчас на кривой AB последовательность точек , идущих друг за другом в указанном направлении. Им отвечает последовательность возрастающих значений параметра . Впишем в кривую AB ломаную и обозначим через p её периметр. Конечный предел s для периметра p , при рвении к нулю громаднейшей из сторон ломаной ( p ), именуется длиной дуги : . В случае, если таковой предел существует, то сама кривая именуется спрямляемой .
Перейдём конкретно к выражению длины дуги интегралом.
Предположим дополнительно, что функции и , фигурирующие в уравнениях (8) незамкнутой кривой, имеют постоянные производные и .
При этих условиях, как мы докажем, кривая спрямляема и протяженность дуги выражается формулой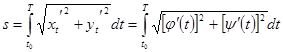 
. (9)
Будем исходить из разбиения промежутка точками на части длины . Этим значениям t отвечают вершины ломаной , вписанной в дугу , и длину её возможно выяснить как предел периметра P ломаной при рвении к нулю. Положим , и , .
Протяженность i -ого звена вписанной ломаной выразится так: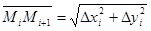 
.
Применив к функции и приращениям порознь формулу конечных приращений, возьмём:
, , причём о значениях и мы ничего не знаем, помимо этого, что оба они находятся между и . Имеем сейчас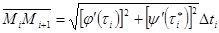 
, так что для периметра всей ломаной получается следующее выражение:
.
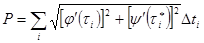В случае, если заменить во втором слагаемом под знаком корня везде на , то преобразованное выражение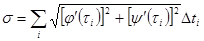 
, разумеется, представит собой интегральную сумму именно для интеграла (9). При рвении к нулю эта сумма и будет своим пределом упомянутый интеграл. Чтобы продемонстрировать, что к тому же пределу пытается и периметр P ломаной, достаточно понять, что разность пытается к нулю.
С целью этого произведём оценку данной разности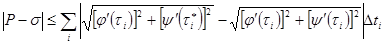 
. Элементарное неравенство 
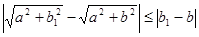, в случае, если применить его к каждому слагаемому написанной выше суммы в отдельности, даст нам 
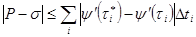. Ввиду непрерывности функции , по любому заданному найдётся такое , только лишь . В случае, если забрать все , так что и 
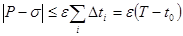. Это и обосновывает отечественное утверждение.
В случае, если кривая задана явным уравнением в прямоугольных координатах , то, принимая x за параметр, из формулы (9), как её частный случай, возьмём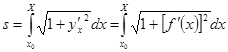 
. (9а)
Наконец, и случай полярного задания кривой кроме этого приводится к параметрическому посредством простых формул перехода , ; роль параметра тут играется . Для этого случая , , так что и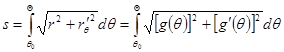 
. (9б)
Примеры:
1). Парабола: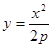 
. Приняв за начало отсчёта дуг вершину O ( x =0) , для произвольной точки M c абсциссой x имеем:
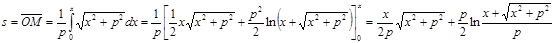
2). Эллипс: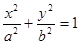 
. Эргономичнее забрать уравнение эллипса в параметрической форме: , . Разумеется,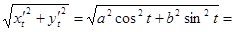 
, где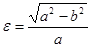 
имеется численный эксцентриситет эллипса. Вычисляя длину дуги эллипса от верхнего финиша малой оси до любой его точки в первом квадранте, 
.
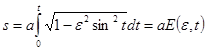Так, протяженность дуги эллипса выражается эллиптическим интегралом второго рода; как указывалось, данный факт послужил предлогом для заглавия «эллиптический».
В частности, протяженность четверти обвода эллипса выражается через полный эллиптический интеграл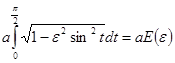 
. Протяженность же всего обвода будет .
Количество тела
Начнём с практически очевидного замечания: прямой цилиндр высоты H , основанием которого помогает квадрируемая плоская фигура ( P ), имеет количество, равный произведению площади основания на высоту: .
Заберём многоугольники и , соответственно содержащиеся в (P ), так, дабы их площади и стремились к P. В случае, если на этих многоугольниках выстроить высоты и прямые призмы H , то их количества и будут стремиться к неспециализированному пределу , что и будет количеством отечественного цилиндра
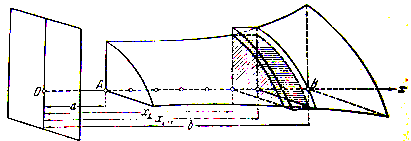
Разглядим сейчас некое тело (V ), содержащееся между плоскостями и , и начнём рассекать его плоскостями, перпендикулярными к оси x (чертёж 7). Допустим, что (чертёж 7) все эти сечения квадрируемы, и пускай площадь сечения, отвечающего абсциссе x , — обозначим её через P ( x ) – будет постоянной функцией от x (для ).
В случае, если спроектировать без искажения два аналогичных сечения на какую-либо плоскость, перпендикулярную к оси x , то они смогут или находиться одно в другом (чертёж 8а), или частично одно на второе налегать, (чертёж 
либо лежать одно вне другого (чертёж 8б и 8в). Мы остановимся на том случае, в то время, когда два разных сечения, будучи спроектированы на плоскость, перпендикулярную к оси x , выясняются в любой момент содержащимися одно в другом.
В этом предположении возможно утверждать, что тело имеет количество, что выражается формулой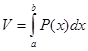 
. (5)
Для доказательства разобьём отрезок на оси x точками на части и разложим плоскостями , совершёнными через точки деления, всё тело на слои . Разглядим i -й слой, содержащийся между плоскостями и (i = 0,1,…,n -1). В промежутке функция P (x) имеет громаднейшее значение и . В случае, если сечения, отвечающие разным значениям x в этом промежутке, поместить на одну плоскость, скажем, , то все они при сделанном предположении будут находиться в громаднейшем, имеющем площадь , и содержать в себе мельчайшее, с площадью . В случае, если на этих, громаднейшем и мельчайшем, сечениях выстроить прямые цилиндры высоты , то больший из них будет содержать в себе разглядываемый слой отечественного тела, а меньший сам будет находиться в этом слое. На основании сделанного сначала замечания количества этих цилиндров будут, соответственно, и .
Из входящих цилиндров составится тело (T ), а из выходящих – тело (U ). Их количества равны, соответственно,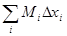 
и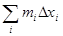 
и, в то время, когда пытается к нулю , имеют неспециализированный предел (5). Значит таков же будет и количество тела(V ).
Ответственный частный случай, в то время, когда заведомо выполняется указанное выше предположение о обоюдном размещении сечений, воображают тела вращения . Вообразим на плоскости xy кривую, заданную уравнением , где постоянна и неотрицательна. Начнём вращать ограниченную её криволинейную трапецию около оси x (чертёж 9а и 9б). Полученное тело (V ), разумеется, подходит под разглядываемый случай, потому что сечения его проектируются на перпендикулярную к оси x плоскость в виде концентрических кругов. Тут , так что
.
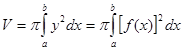В случае, если криволинейная трапеция ограничена (чертёж 9)
и сверху и снизу кривыми и , то разумеется,
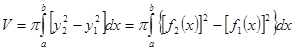, (7)
Не смотря на то, что предположение о сечениях тут может и не выполняться. По большому счету доказанный итог легко распространяется на все такие тела, каковые получаются путём сложения либо вычитания из тел, удовлетворяющих упомянутому предположению.
В общем случае возможно утверждать только следующее: в случае, если тело ( V ) имеет количество, то он выражается формулой (6).
Примеры: 1). Пускай эллипс 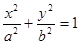вращается около оси x . Так как 
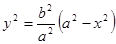, то для количества эллипсоида вращения отыщем
.
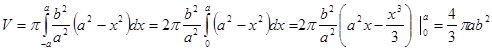Подобно для количества тела, взятого от вращения около оси y , отыщем выражение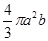 
. Предполагая же в этих формулах , мы возьмём для количества щара радиуса r известное значение 
.
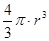2). То же – для ветви циклоиды , ( ). Параметрическое уравнение кривой облегчают исполнение подстановки , в формуле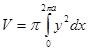 
. Конкретно:
.
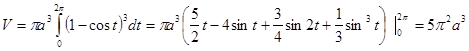3). Отыскать количество трёхосного эллипсоида, заданного каноническим уравнением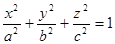 
(чертёж 10).
Плоскость, перпендикулярная к оси x и проходящая через точку M ( x ) на данной оси, пересечёт эллипсоид по эллипсу. Уравнение проекции его (без искажения) на плоскость yz будет таково: (чертёж 10).
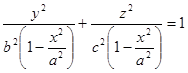, (x =const).
Отсюда ясно, что полуоси его будут, соответственно,
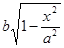и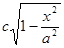 
,
а площадь выразится так: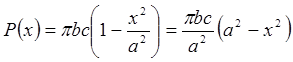 
.
Так, по формуле (5) искомый количество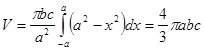 
.
Способ прямоугольников
Способ трапеций
Способ Симпсона (парабол)
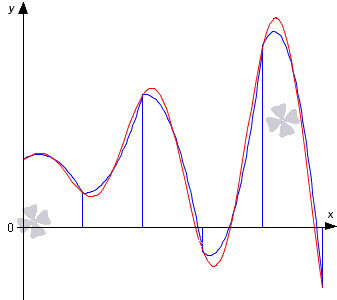
Задача нахождения правильного значения определенного интеграла не всегда имеет ответ. Вправду, первообразную подынтегральной функции во многих случаях не удается представить в виде элементарной функции. В этом случае мы не можем совершенно верно вычислить определенный интеграл по формуле Ньютона-Лейбница. Но имеется способы численного интегрирования, разрешающие взять значение определенного интеграла с требуемой степенью точности. Одним из таких способов есть способ Симпсона (его еще именуют способом парабол).
Сперва узнаем суть способа парабол, дадим графическую иллюстрацию и выведем формулу для вычисления приближенного значения интеграла. Потом запишем неравенство для оценки безотносительной погрешности способа Симпсона (парабол). Следом перейдем к ответу характерных примеров, снабдим их подробными комментариями. В заключении сравним способ Симпсона с методом трапеций и методом прямоугольников.
Навигация по странице.
- Способ парабол (Симпсона) — сущность способа, формула, оценка погрешности, иллюстрация.
- Примеры приближенного вычисления определенных интегралов способом Симпсона (парабол).
Способ парабол (Симпсона) — сущность способа, формула, оценка погрешности, иллюстрация.
Пускай функция y = f(x) постоянна на отрезке [a; b] и нам требуется вычислить определенный интеграл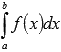 
.
Разобьем отрезок [a; b] на n элементарных отрезков длины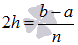 
точками . Пускай точки являются серединами отрезков соответственно. В этом случае все узлы определяются из равенства .
Сущность способа парабол.
На каждом промежутке подынтегральная функция приближается квадратичной параболой , проходящей через точки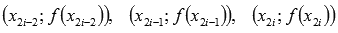 
. Из этого и наименование способа — способ парабол.
Это делается чтобы в качестве приближенного значения определенного интеграла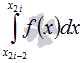 
забрать 
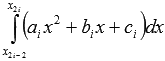, что мы можем вычислить по формуле Ньютона-Лейбница. В этом и содержится сущность способа парабол.
Геометрически это выглядит так:
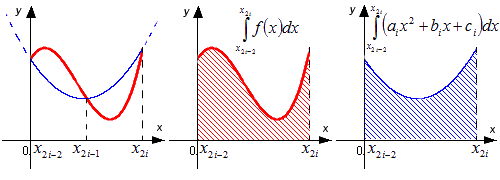
Графическая иллюстрация способа парабол (Симпсона).
Красной линией изображен график функции y=f(x), синей линией продемонстрировано приближение графика функции y=f(x) квадратичными параболами на каждом элементарном отрезке разбиения.
ТЕМА 2.1. ЗАДАЧИ. ПРИВОДЯЩИЕ К ВЫЧИСЛЕНИЮ ИНТЕГРАЛОВ
Определенный интеграл
Определённым интегралом от постоянной функции f(x) на конечном отрезке [a, b] (где ) именуется приращение какой-нибудь её первообразной на этом отрезке. (По большому счету, познание заметно облегчится, в случае, если повторить тему неизвестного интеграла) Наряду с этим употребляется запись
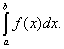
Как видно на графиках внизу (приращение первообразной функции обозначено ), определённый интеграл возможно как хорошим, так и отрицательным числом (Вычисляется как разность между значением первообразной в верхнем пределе и её же значением в нижнем пределе, т. е. как F(b) — F(a)).
Числа a и b именуются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.
Так, в случае, если F(x) – какая-нибудь первообразная функция для f(x), то, в соответствии с определению,
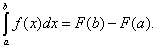
Равенство (38) именуется формулой Ньютона-Лейбница. Разность F(b) – F(a) коротко записывают так:
Исходя из этого формулу Ньютона-Лейбница будем записывать и без того:
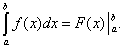
Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции забрана при его вычислении. Пускай F(x) и Ф(х) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х) = F(x) + C. Исходя из этого
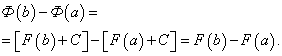
Тем самым установлено, что на отрезке [a, b] приращения всех первообразных функции f(x) совпадают.