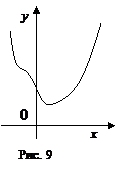При ответе задач с параметром часто бывает нужно строить график некоей функции. В несложных случаях (квадратичная, дробно-линейная функции) возможно обойтись без производной, но более сложные графики строим с применением производной. При построении графиков функций будем пользоваться сокращенной схемой изучения, складывающейся из трех пунктов: 1) нахождение области определения; 2) определение промежутков и нулей функции знакопостоянства; 3) нахождение промежутков и экстремумов монотонности.
1. Выяснить число ответов уравнения в зависимости от параметра. Ответ. Строим график функции . Для этого находим производную . Приравниваем ее к нулю, дабы отыскать точки экстремумов и убывания монотонности (и промежутки возрастания). Уравнение имеет корни . Составим таблицу монотонности.
| + | – | + | |||
| –2 |
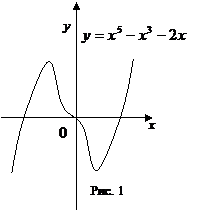
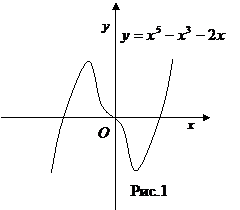Напомним, что функция обращается в ноль в точках , 
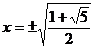. Эти сведенья разрешают выстроить схему графика (на рисунке представлен более надежный график, выстроенный с применением второй производной, но для ответа данной задачи такая точность не необходима). В мыслях двигая горизонтальную прямую , вычисляем число точек пересечения с графиком. Приобретаем при одно ответ, при два решения, при три решения. Ответ: при одно ответ, при два решения, при три решения.
2. Выстроить график функции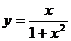 
. Выяснить, при каких значениях параметра уравнение 
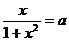имеет хотя бы один корень в промежутке . Ответ. Находим производную 
= 
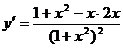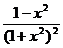. Приравниваем ее к нулю, дабы отыскать точки экстремумов и промежутки монотонности: 
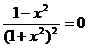, . Составим таблицу монотонности.
| – | + | – | |||
| –0,5 | 0,5 |
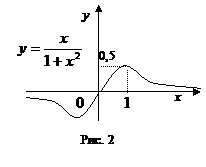Напомним, что функция обращается в ноль в точке , при хороша, а при отрицательна. Эта функция имеет кроме этого серьёзную изюминку: при неограниченном повышении значения функции стремятся к нулю, поскольку знаменатель содержит в более высокой степени, чем числитель. Эту особенность нужно отразить на чертеже, «устремляя» график к оси абсцисс при удалении «на бесконечность». Сейчас выделим часть графика, соответствующую (рис. 3). Для этого определим значения , . По чертежу видно, что уравнение 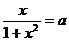имеет ответ, находящиеся в собствености промежутку , в том случае, в то время, когда . Ответ: .
3. 
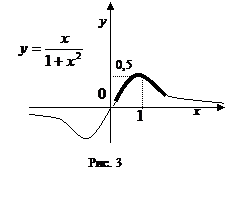Выстроить график функции 
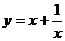. Выяснить, при каких значениях параметра уравнение 
имеет два разных корня в промежутке . Ответ. Область определения . Находим производную 
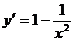
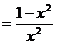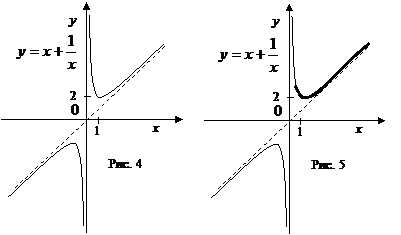
. Приравниваем ее к нулю, дабы отыскать точки экстремумов и промежутки монотонности: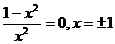 
. В таблицу монотонности нужно внести колонку для той точки, в которой производная не существует, т. е. . Приобретаем график на рис. 4.
| + | – | Не сущ. | – | + | |||
| –2 | Не сущ. | ||||||
Сейчас выделим часть графика, соответствующую (рис. 5). Для этого определим значения . По чертежу видно, что уравнение имеет два разных ответы, которыми владел промежутку , в том случае, в то время, когда . Ответ: .
4. При каких значениях параметра уравнение имеет хотя бы один корень? Ответ.Преобразуем уравнение к виду , . Положим и выстроим график функции с областью определения . Находим производную . Приравниваем ее к нулю, дабы отыскать точки экстремумов и промежутки монотонности: , . Составим таблицу монотонности:
| + | – | + | |||
| –1 |
Определим значение функции в точке : . Сейчас можем выстроить график (рис. 6). По графику видно, что уравнение имеет ответ, находящиеся в собствености множеству , в случае, если . Ответ: .
5. 
 |
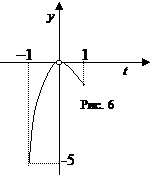
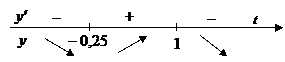При каких значениях уравнение имеет ответ? Ответ.Применим формулу тройного довода: . Возьмём уравнение . Положим и выстроим график функции с областью определения . Находим производную . Находим нули производной , и составим таблицу монотонности. Определим значения функции в точках экстремумов и на финишах отрезков: ; ; . Следовательно, множество значений – это отрезок . Ответ: .
6. Решить уравнение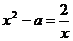 
при условии, что оно имеет ровно два разных корня. Ответ. Разглядим функцию 
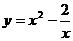и выстроим ее график. Для этого отыщем производную 
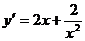. Так как производная обращается в 0 лишь в точке (наряду с этим ), приобретаем таблицу монотонности на рис. 7, с учетом которой строим график (рис.8). Приобретаем, что ровно два корня уравнение 
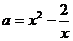имеет при и один из этих корней . Остается отыскать второй корень уравнения 
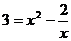. Так как – корень уравнения , то возможно выделить сомножитель : . Из уравнения приобретаем . Ответ: .
7.
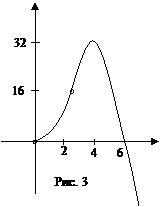При каких значениях параметра уравнение 
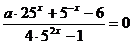имеет ровно один корень? Ответ.Изучение будет мало несложнее, в случае, если ввести замену . Тогда уравнение примет вид 
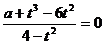. Это уравнение должно иметь ровно один хороший корень. Данное условие равносильно тому, что уравнение имеет ровно один хороший корень, не равный 2 ( не входит в ОДЗ). Изобразим график функции , (рис. 3). Для этого отыщем производную , точки экстремумов и . Точку нужно «выколоть». Проследим, при каких значениях прямая имеет с графиком ровно одну точку пересечения. По графику видно, что это условие выполняется при . Ответ: .
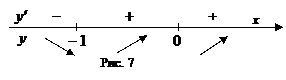
8. 
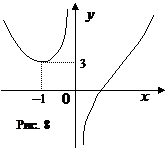Определить значение , при котором есть точкой максимума функции . Ответ. Находим производную . Приравниваем ее к нулю, дабы отыскать точки экстремумов и промежутки монотонности: , . В этом случае, разумеется, что — больший корень, причем производная хороша при и при , а между корнями она отрицательна.. Значит, максимум функции находится в точке . Из этого . Ответ: 7.
9. При каких значениях функция убывает на всей числовой прямой? Ответ. Отыщем производную . Дабы функция , постоянная на всей числовой прямой, являлась везде убывающей, потребуем, дабы для всех выполнялось неравенство . Квадратичная функция не меняет символ на всей числовой прямой, в случае, если ее дискриминант . Приобретаем неравенство .
10. При каких значениях параметра функция возрастает на всей числовой прямой? Ответ. Отыщем производную . Дабы эта функция являлась везде возрастающей, потребуем, дабы для всех выполнялось неравенство . Обозначим и возьмём неравенство , либо, учитывая , , которое обязано выполняться для всех . Решим соответствующее квадратное уравнение и возьмём корни , . Разумеется, условие выполняется в том и лишь в том случае, если оба корня не хороши, т. е. , либо . Ответ: .
11. *При каких значениях параметра функция возрастает при всех ? Ответ.Отыщем производную . Дабы эта функция являлась возрастающей при всех , потребуем, дабы для всех выполнялось неравенство . Это выполнено при условии , либо . Ответ: .
12. При каком функция не имеет экстремума в критической точке? Ответ. Находим производную . Дабы в критической точке не было экстремума, необходимо, дабы в данной точке производная обращалась в ноль, но не меняла символа. Это быть может, в случае, если квадратный трехчлен есть полным квадратом, т. е. его дискриминант равен нулю: . Из этого . Ответ: .
13. При каком функция имеет хорошую точку максимума? Ответ. Находим производную . Приравниваем ее к нулю . Корни этого уравнения . Если судить по распределению знаков , максимум должен быть в точке, соответствующей меньшему корню, в этом случае . Значит, должно выполняться неравенство . Решаем неравенство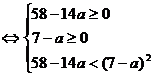 
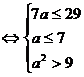. Ответ: .
14. На рисунке 9 изображен график функции . Выяснить символы коэффициентов . Ответ. Символы и определяются легко: , так как точка пересечения с осью Оу лежит выше оси Ох. Так как при , то . Дабы выяснить символ , отыщем производную: , число – это значение производной в точке 0. Но по углу наклона касательной в точке пересечения с осью ординат (либо по тому, что функция в окрестности данной точки убывает) мы можем сделать вывод, что производная в данной точке отрицательна, т. е. . Ответ: .
