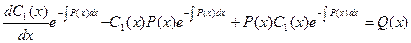
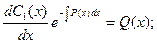
Из этого уравнения определим переменную функцию С1(х):
Интегрируя, приобретаем:
Подставляя это значение в исходное уравнение, приобретаем:
.
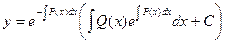Так, мы взяли итог, абсолютно совпадающий с результатом расчета по способу Бернулли.
При выборе способа ответа линейных дифференциальных уравнений направляться руководствоваться простотой интегрирования функций, входящих в исходный интеграл.
Потом разглядим примеры ответа разных дифференциальных уравнений разными способами и сравним результаты.
Пример. Решить уравнение
Сперва приведем данное уравнение к стандартному виду: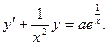 
Применим взятую выше формулу: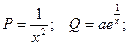 
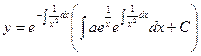
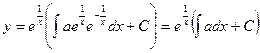
Уравнение Бернулли.
Определение. Уравнением Бернуллиназывается уравнение вида
где P и Q – функции от х либо постоянные числа, а n – постоянное число, не равное 1.
Для решения уравнения Бернулли используют подстановку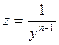 
, благодаря которой, уравнение Бернулли приводится к линейному.
Для этого поделим исходное уравнение на yn.
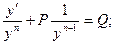
Применим подстановку, учтя, что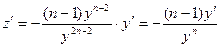 
.
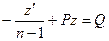
Т.е. оказалось линейное уравнение довольно малоизвестной функции z.
Ответ этого уравнения будем искать в виде:
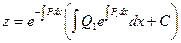
Пример. Решить уравнение
Поделим уравнение на xy2: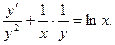 
Полагаем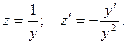 
.
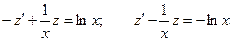Полагаем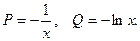 
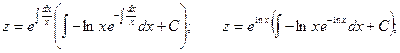
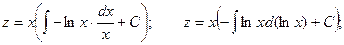
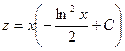
Произведя обратную подстановку, приобретаем:
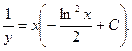
Пример. Решить уравнение
Поделим обе части уравнения на
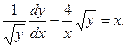
Полагаем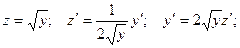 
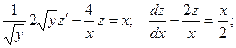
Взяли линейное неоднородное дифференциальное уравнение. Разглядим соответствующее ему линейное однородное уравнение:
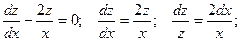
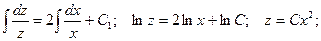
Полагаем C = C(x) и подставляем полученный итог в линейное неоднородное уравнение, с учетом того, что:
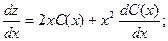
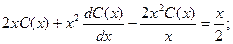
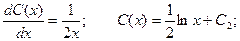
Приобретаем: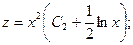 
Используя обратную подстановку, приобретаем окончательный ответ:
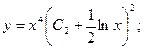
Уравнения в полных дифференциалах (тотальные).
Определение. Дифференциальное уравнение первого порядка вида:
именуется уравнением в полных дифференциалах, в случае, если левая часть этого уравнения представляет собой полный дифференциал некоей функции
Интегрирование для того чтобы уравнения сводится к нахождению функции u, по окончании чего ответ легко находится в виде:
Так, для ответа нужно выяснить:
1) в каком случае левая часть уравнения представляет собой полный дифференциал функции u;
2) как отыскать эту функцию.
В случае, если дифференциальная форма есть полным дифференциалом некоей функции u, то возможно записать:
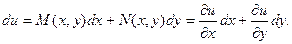
Т.е.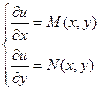 
.
Отыщем смешанные производные второго порядка, продифференцировав первое уравнение по у, а второе – по х:
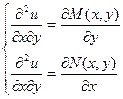
Приравнивая левые части уравнений, приобретаем нужное и достаточное условие того, что левая часть дифференциального уравнения есть полным дифференциалом. Это условие кроме этого именуется условием тотальности.
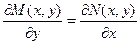
Сейчас разглядим вопрос о нахождении фактически функции u.
Проинтегрируем равенство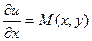 
:
Благодаря интегрирования приобретаем не постоянную величину С, а некую функцию С(у), т.к. при интегрировании переменная у надеется постоянным параметром.
Определим функцию С(у).
Продифференцируем полученное равенство по у.
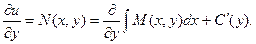
Откуда приобретаем: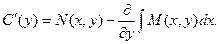 
Для нахождения функции С(у) нужно проинтегрировать приведенное выше равенство. Но, перед интегрированием нужно доказать, что функция С(у) не зависит от х. Это условие будет выполнено, в случае, если производная данной функции по х равна нулю.
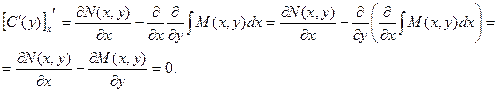
Сейчас определяем функцию С(у):
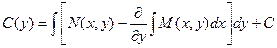
Подставляя результат в выражение для функции u, приобретаем:
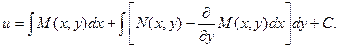
Тогда неспециализированный интеграл исходного дифференциального уравнения будет иметь вид:
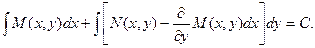
направляться подчернуть, что при ответе уравнений в полных дифференциалах не обязательно применять взятую формулу. Ответ может оказаться более компактным, в случае, если способу, которым формула была взята.
Пример. Решить уравнение
Удостоверимся в надежности условие тотальности: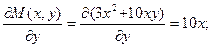 
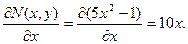
Условие тотальности выполняется, следовательно, исходное дифференциальное уравнение есть уравнением в полных дифференциалах.
Определим функцию u.
;
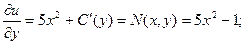
Итого,
Находим неспециализированный интеграл исходного дифференциального уравнения:
Уравнения вида y = f(y’) иx = f(y’).
Ответ уравнений, не содержащих в одном случае довода х, а в другом – функции у, ищем в параметрической форме, принимая за параметр производную малоизвестной функции.
Для уравнения первого типа приобретаем: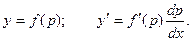 
Делая замену, приобретаем: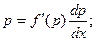 
В следствии этих преобразований имеем дифференциальное уравнение с разделяющимися переменными.
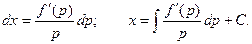
Неспециализированный интеграл в параметрической форме представляется совокупностью уравнений:
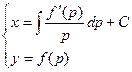
Исключив из данной совокупности параметр р, возьмём неспециализированный интеграл и не в параметрической форме.
Для дифференциального уравнения вида x = f(y’) посредством той же аналогичных рассуждений и самой подстановки приобретаем итог:
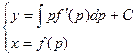
Уравнения Лагранжа и Клеро.
( Алекси Клод Клеро (1713 – 1765) французский математик
ин. поч. член Петерб. АН )
Определение. Уравнением Лагранжаназывается дифференциальное уравнение, линейное довольно х и у, коэффициенты которого являются функциями от y’.
Для нахождения неспециализированного ответ используется подстановка p = y’.
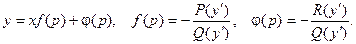
Дифференцируя это уравнение,c учетом того, что , приобретаем:
В случае, если ответ этого (линейного довольно х) уравнения имеется то неспециализированное ответ уравнения Лагранжа возможно записано в виде:
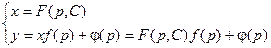
Определение. Уравнением Клероназывается уравнение первой степени (т.е. линейное) относительно функции и аргумента вида:
По большому счету говоря, уравнение Клеро есть частным случаем уравнения Лагранжа.
С учетом замены , уравнение принимает вид:
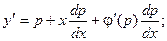
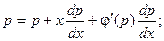
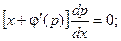
Это уравнение имеет два вероятных ответы:
либо
В первом случае:
Видно, что неспециализированный интеграл уравнения Клеро является семейством прямых линий.
Во втором случае ответ в параметрической форме выражается совокупностью уравнений:
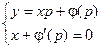
Кроме параметр р, приобретаем второе ответ F(x, y) = 0. Это решение не содержит произвольной постоянной и не получено из неспециализированного ответа, следовательно, не есть частным ответом.
Это решение будет являться особенным интегралом. ( См. Особенное ответ. )
Потом разглядим примеры ответа разных типов дифференциальных уравнений первого порядка.
Пример. Решить уравнение с заданными начальными условиями.
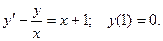
Это линейное неоднородное дифференциальное уравнение первого порядка.
Решим соответствующее ему однородное уравнение.
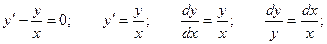
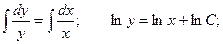
Для неоднородного уравнения неспециализированное ответ имеет форму:
Дифференцируя, приобретаем:
Для нахождения функции С(х) подставляем полученное значение в исходное дифференциальное уравнение:
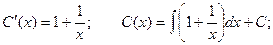
Итого, неспециализированное ответ:
C учетом начального условия определяем постоянный коэффициент C.
Совсем приобретаем:
Для проверки подставим полученный итог в исходное дифференциальное уравнение: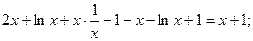 
правильно
Ниже продемонстрирован график интегральной кривой уравнения.
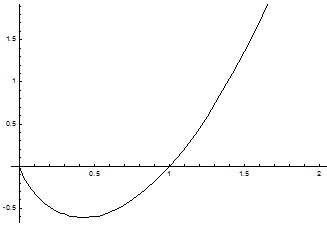
Пример. Отыскать неспециализированный интеграл уравнения .
Это уравнение с разделяющимися переменными.
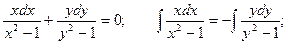
Неспециализированный интеграл имеет форму:
Выстроим интегральные кривые дифференциального уравнения при разных значениях С.
С = — 0,5 С = -0,02 С = -1 С = -2
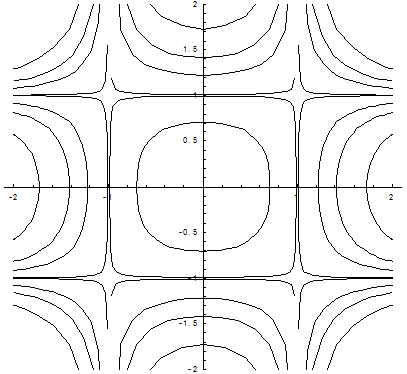
С = 0,02 С = 0,5 С = 1 С = 2
Пример. Отыскать ответ дифференциального уравнения, удовлетворяющее заданным начальным условиям.
Это уравнение с разделяющимися переменными.
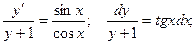
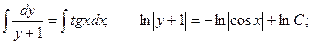
Неспециализированное ответ имеет форму: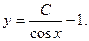 
Отыщем частное ответ при заданном начальном условии у(0) = 0.
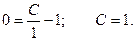
Совсем приобретаем: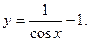 
Пример. Решить прошлый пример вторым методом.
Вправду, уравнение возможно рассмотрено как линейное неоднородное дифференциальное уравнение.
Решим соответствующее ему линейное однородное уравнение.
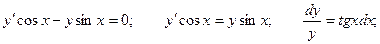
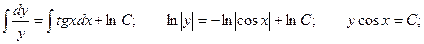
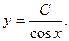
Ответ неоднородного уравнения будет иметь вид: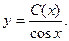 
Тогда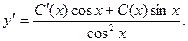 
Подставляя в исходное уравнение, приобретаем:
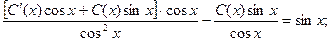
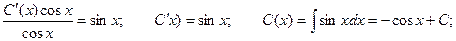
Итого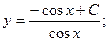 
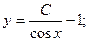
С учетом начального условия у(0) = 0 приобретаем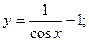 
Как видно результаты, полученные при ответе данного дифференциального уравнения разными методами, совпадают.
При ответе дифференциальных уравнений не редкость допустимо выбирать способ ответа, исходя из сложности преобразований.
Пример. Решить уравнение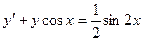 
с начальным условием у(0) = 0.
Это линейное неоднородное уравнение. Решим соответствующее ему однородное уравнение.
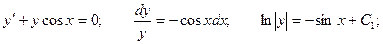
Для линейного неоднородного уравнения неспециализированное ответ будет иметь вид:
Для определения функции С(х) отыщем производную функции у и подставим ее в исходное дифференциальное уравнение.
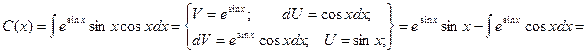
Итого
Удостоверимся в надежности полученное неспециализированное ответ подстановкой в исходное дифференциальное уравнение.
(правильно)
Отыщем частное ответ при у(0) = 0.
Совсем
Пример. Отыскать ответ дифференциального уравнения
с начальным условием у(1) = 1.
Это уравнение возможно преобразовано и представлено как уравнение с поделёнными переменными.
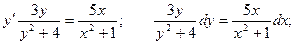
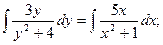
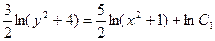
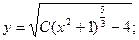
С учетом начального условия:
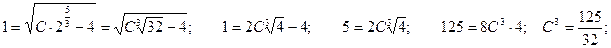
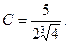
Совсем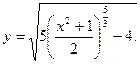 
Пример. Решить дифференциальное уравнение с начальным условием у(1) = 0.
Это линейное неоднородное уравнение.
Решим соответствующее ему однородное уравнение.
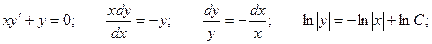
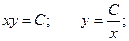
Ответ неоднородного уравнения будет иметь вид:
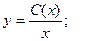
Подставим в исходное уравнение:
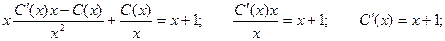
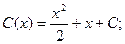
Неспециализированное ответ будет иметь вид: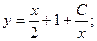 
C учетом начального условия у(1) = 0: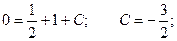 
Частное ответ: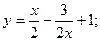 
Пример. Отыскать ответ дифференциального уравнения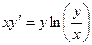 
с начальным условием у(1) = е.
Это уравнение возможно приведено к виду уравнения с разделяющимися переменными посредством замены переменных.
Обозначим: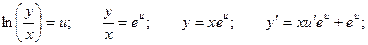 
Уравнение принимает вид:
Взяли уравнение с разделяющимися переменными.
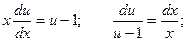
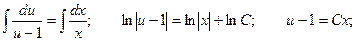
Сделаем обратную замену: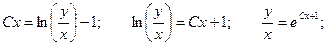 
Неспециализированное ответ:
C учетом начального условия у(1) = е:
Частное ответ:
Второй метод ответа.
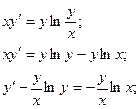
Взяли линейное неоднородное дифференциальное уравнение. Соответствующее однородное:
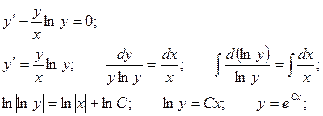
Ответ исходного уравнения ищем в виде:
Подставим полученные результаты в исходное уравнение:
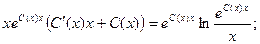
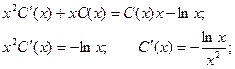
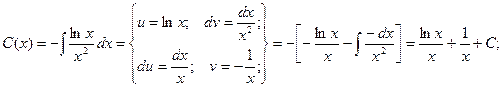
Приобретаем неспециализированное ответ:
Пример. Решить дифференциальное уравнение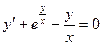 
с начальным условием у(1)=0.
В этом уравнении кроме этого комфортно применить замену переменных.
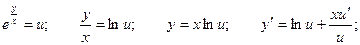
Уравнение принимает вид: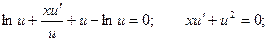 
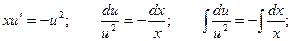
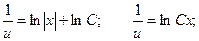
Делаем обратную подстановку: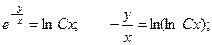 
Неспециализированное ответ:
C учетом начального условия у(1) = 0:
Частное ответ:
Второй метод ответа.
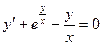
Замена переменной: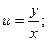 
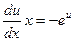
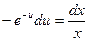
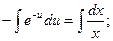
Неспециализированное ответ: