В технических совокупностях замкнутые термодинамические совокупности, в которых имеет место равновесное состояние, видится весьма редко. По большей части, в технических устройствах рабочее вещество, их заполняющее, будет в неравновесном состоянии. Это ведет к происхождению потока вещества, перемещающего вещество из одной точки устройства в другую. Исходя из этого разглядывать какую-то часть устройств в виде замкнутой совокупности запрещено, соответственно, нельзя применять к ней 1 — ый закон термодинамики для замкнутой совокупности. Для описания таких устройств видоизменяют данный закон. В следствии появляется 1 — ый закон термодинамики для открытой термодинамической совокупности, частным случаем которой есть поток. Он имеет следующее математическое выражение
 . |
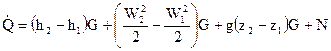(79) |
В этом выражении
— тепловой поток, подводимы к участку канала между двумя сечениями 1 и 2, Вт;
h1 и h2 – энтальпии потока в сечениях 1и 2;
W1 и W2 – скорости потока в сечениях 1 и 2;
z1 и z2 – координаты центров тяжестей сечений 1 и 2 над поверхностью уровня;
N – мощность, отводимая от потока каким – или техническим устройством, расположенным между сечениями 1 и 2, Вт;
G – массовый расход вещества через сечение канала, ж
g – ускорение свободного падения, .
Выражение (79) показывает, что тепловой поток, подведённый к каналу между двумя сечениями , затрачивается на трансформацию внутренней энергии потока , на трансформацию кинетической энергии потока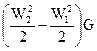 
, на трансформацию потенциальной энергии потока в поле силы тяжести и на отвод механической мощности N.
1 – ый закон термодинамики для потока возможно выразить через удельные размеры, в случае, если обе части поделить на G
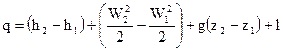 либо в более краткой форме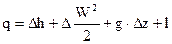 
|
(80) |
В этих выражениях
q – удельная теплота, подводимая к одному килограмму вещества в потоке, ;
l – удельная работа, отводимая от одного килограмма вещества в потоке, .
Уравнения (80) представляет собой интегральную форму уравнения 1-го закона термодинамики, в то время, когда расстояние между сечениями конечное. В случае, если же расстояние между сечениями 1 и 2 бесконечно малое, то изменение размеров, входящих в уравнение (80), преобразуется в бесконечно малое изменение, и получаются дифференциальные уравнения первого закона термодинамики для потока
введем в рассмотрение энтропию торможения.
 , 
|
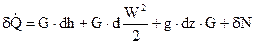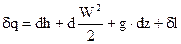
(81) |
В случае, если поток есть горизонтальным (расстояние между сечениями меньше размеров сечений), то в этом случаи трансформацией потенциальной энергии силы тяжести возможно пренебречь, и уравнение (80) возможно подставить в виде
|
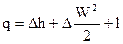
(82) |
В случае, если горизонтальный поток между разглядываемыми сечениями не делает механической работы, то
 , . |
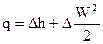(83) |
В случае, если наряду с этим поток есть адиабатным, то
 , . |
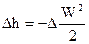(84) |
В случае, если скорость потока в этом случае изменятся при переходе от сечения к сечению незначительно (при канала постоянного сечения), то
| , , т.е. | (85) |
Уравнение (85) показывает, что внутренняя энергия горизонтального адиабатного, не делающего механической работы потока, движущегося в канале постоянного сечения, не изменяется.
Из уравнения (84) возможно выразить скорость во втором сечении
| . | (86) |
Из этого уравнения направляться, что чтобы расширить скорость потока в сечении 2, нужно между этими сечениями уменьшить энтальпию. В случае, если же в сечении 1 поток покоится (поток вытекает из сосуда громадного количества), W1=0 тогда
| . | (87) |
Уравнение (87) характеризует максимально вероятную скорость, которую возможно взять при истечении из сосуда через суживающееся отверстие либо канал.
Главные термодинамические процессы в области газа
К главным термодинамическим процессам относиться: изохорный, изобарный, изотермический, адиабатный, политропный и процесс дросселирования.
Изохорный процесс
Изохорный процесc- это процесс, протекающий при постоянном количестве
V=ConsT; dV=0.
Для совершенного газа уравнение изохорного процесса, связывающие между собой главные термодинамические параметры, вытекает из уравнения состояния совершенного газа.
В случае, если m и V – постоянные размеры, то неизменно и отношение
.
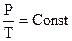Это же соотношение возможно выразить через начальные и конечные параметры
 . |
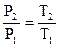(88) |
Уравнение (88) и есть уравнением изохорного процесса. Из него направляться, что при повышении температуры давление газа возрастает.
Работа в изохорном ходе равна нулю
,
т.к. колличество газа не изменяется. Исходя из этого теплота, подведенная либо отведенная, определяется, на базе 1-го закона термодинамики, как
| , , | (89) |
где m – масса газа.
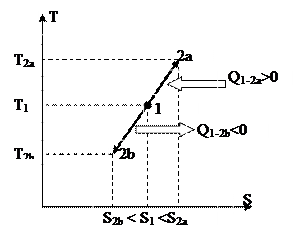
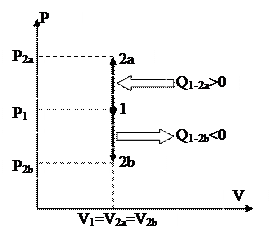
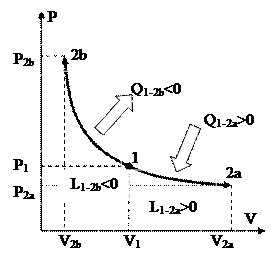
Изображение изохорных процессов в P-V диаграмме представлено на рис. 19
 |
|||
 |
|||
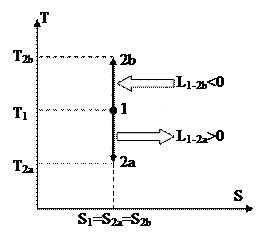
Рис. 19 Рис. 20.
Процесс 1-2a протекает с увеличением давления, 1-2b – с понижением. Т.к. давление в ходе 1-2a увеличивается, то, в силу (88), возрастает и температура, что, со своей стороны говорит о том (см. (89)), что теплота хороша, т.е. подводится. В ходе 1-2b теплота отрицательна и отводится.
Чтобы получить изображение изохорного процесса и T-S диаграмме, нужно взять зависимость температуры T от энтропии s для изохорного процесса. Для этого подставив выражение в (45), возьмём
.
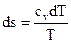Проинтегрировав это выражение в пределах от T1 до T, возьмём
.
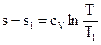Из этого уравнения направляться, что
 . |
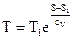(90) |
Так, изохора в T-S диаграмме есть графиком экспоненты, которую, учитывая удалённость разглядываемой области от начала координат, возможно изображать наклонной прямой (см. рис. 20).
Изобарный процесс
Изобарный процесc- это процесс, протекающий при постоянном давлении
P=ConsT; dP=0.
Для совершенного газа уравнение изобарного процесса, связывающие между собой главные термодинамические параметры, вытекает из уравнения состояния совершенного газа.
В случае, если m и Р – постоянные размеры, то неизменно и отношение
.
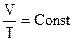Это же соотношение возможно выразить через начальные и конечные параметры
 . |
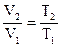(91) |
Уравнение (88) и есть уравнением изобарного процесса. Из него направляться, что при повышении температуры колличество газа возрастает.
Работа в изохорном ходе определяется выражением
 . |
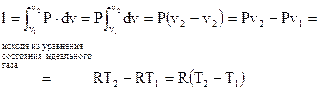(92) |
Предпоследнее равенство основано на уравнении состояния совершенного газа.
Количество теплоты, которым совокупность обменялось с окружающей средой, возможно выяснить, с одной стороны, через теплоёмкость
| , | (93) |
а иначе, через первый закон термодинамики
| . | (94) |
Сравнивая выражения (93) и (94), возможно взять уравнение Майера, связывающее изобарную и изохорную теплоёмкости
| , | (95) |
которое справедливо лишь для совершенного газа. Из этого уравнения направляться, что изобарная теплоёмкость газа больше изохорной теплоёмкости.
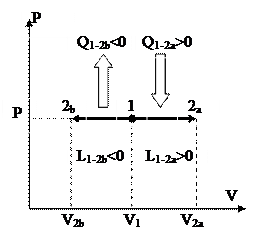
Изображение изобарных процессов в P-V диаграмме представлено на рис. 21
 |
|||
 |
|||
Рис. 21 Рис. 22.
Процесс 1-2a протекает с увеличением количества, 1-2b – с понижением. Исходя из этого работа в ходе 1-2a хороша, т.е. совершается совокупностью, а в ходе 1-2b – отрицательна, т.е подводится к совокупности извне.
Т.к. количество в ходе 1-2a возрастает, то на базе (91) температура возрастает, а это указывает, в соответствии с (93), что теплота хороша и подводится к газу. Соответственно, в ходе 1-2b температура понижается, а теплота отводится, т.е. отрицательна.
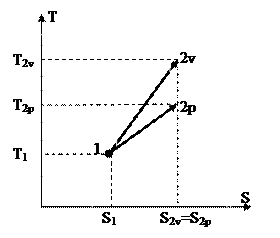
Чтобы получить изображение изохорного процесса и T-S диаграмме, нужно взять зависимость температуры T от энтропии s для изобарного процесса. Рассуждения в этом случае проводятся совершенно верно такие же, как и при изохорного процесса. В следствии получается следующая связь между энтропии и температуры
 . |
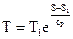(96) |
Отличие от изохорного процесса пребывает в том, что в знаменателе показателя степени экспоненты находится изобарная теплоёмкость. Т.к. она меньше изохорной, то показатель экспоненты в изобарном ходе меньше показателя экспоненты для изохорного процесса. Это значит, что график изохорного процесса в T-S диаграмме идёт «круче» графика изобарного процесса (на рис. 22 изохорный процесс изображён линией 1-2v, а изобарный – линией 1-2р). Данный факт возможно обобщить и утверждать, что изохорный процесс в любой области T-S диаграммы идёт «круче» изобарного.
Изотермический процесс
Изотермический процесс – это процесс, протекающий при постоянной температуре совокупности
T=Const, dT=0
Дабы настоящий процесс, протекающий в природе либо в техническом устройстве, имел возможность принимать во внимание изотермическим, он обязан протекать весьма медлительно, дабы между окружающей средой и системой теплообмен успел случиться.
Для совершенного газа уравнение изотемического процесса выводится из уравнения состояния совершенного газа Pv=RT. В случае, если масса газа в совокупности постоянна, и постоянна температура, то и вся правая часть уравнения состояния совершенного газа постоянна. Это значит, что в изотермическом ходе неизменно произведение объёма и давления. В противном случае говоря, уравнение изотермического процесса имеет форму
| , | (97) |
либо для параметров начального и конечного состояний
| . | (98) |
Работа в изотермическом ходе определяется как интеграл , что вычисляется, учитывая зависимость Р от v, приобретаемую из (97) и(98) Графически зависимость давления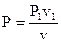 
 . |
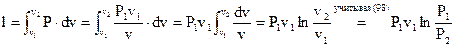(99) |
Из постоянства температуры в изотермическом ходе, для совершенного газа вытекает постоянство внутренней энергии. Это значит, что изменение внутренней энергии в изотермическом ходе у совершенного газа равняется нулю, . Тогда уравнение первого закона термодинамики в этом случае примет вид.
| . | (100) |
В противном случае говоря, в изотермическом ходе теплота, подводимая к совершенному газу, абсолютно преобразуется в работу расширения, которую газ совершает.
Графически связь между объёма и давления 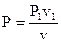является гиперболой , изображённую на рис. 23
 |
 |
Рис. 23 Рис. 24
В поцессе 1-2a колличество газа возрастает, исходя из этого работа хороша (совершается), соответственно хороша (см. (100)) и теплота ( подводится). В поцессе 1-2b количество газауменьшается, исходя из этого работа отрицательна (затрачвается), соответственно отрицательна и теплота (отводится).
Чем выше температура изотермического процесса, тем выше график изотермы находится над осью V в P-V диаграмме (см. рис. 24). Это вытекает из уравнения состояния совершенного газа и из рис. 24, учитывая, что произведение Pv равняется площади прямоугольника с основание v и высотой P.
Изображение изотермического процесса в T-S диаграмме представлено на рис. 25.
 |
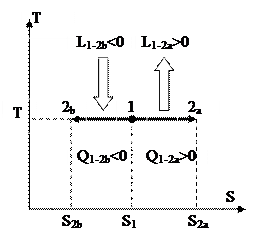Рис. 25.
ЛЕКЦИЯ 9
Адиабатный процесс
Адиабатный процесс протекает без теплообмена между окружающей средой и системой.
Q=0, ?Q=0
Дабы настоящий процесс, протекающий в природе либо в техническом устройстве, имел возможность принимать во внимание адиабатным, он обязан протекать весьма скоро, дабы теплообмен между окружающей средой и системой опоздал случиться.
Уравнение адиабатного процесса для совершенного газа выводиться на базе 1 — ого закона термодинамики
и уравнения состояния совершенного газа
.
Т.к. , то уравнение 1-ого закона термодинамики получает вид
| . | (101) |
Продифференцировав уравнение состояния совершенного газа, возьмём
| . |
либо
 . |
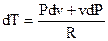(102) |
Учитывая выражение (73), подставим в него (102), а полученный итог – в (101).
В итоге возьмём
 . |
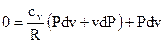Раскрывая скобки в последнем выражении, приводя слагаемые к неспециализированному знаменателю и умножая обе части равенства на R, возьмём
| . |
Собирая слагаемые на базе общности дифференциалов, и учитывая уравнение Майера, возьмём дифференциальное уравнение с разделяющимися переменным
| , |
которое, по окончании разделения переменных принимает вид
 . |
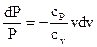Интегрируя последнее уравнение, возьмём
 , |
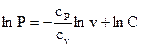где С — произвольная константа.
Избавляясь от логарифмов, это выражение возможно привести к виду
| , | (103) |
которое и есть уравнение адиабатного процесса для совершенного газа.
Введём в рассмотрение показатель адиабаты
 , |
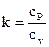(104) |
что кроме этого именуется коэффициентом Пуассона.
Тогда уравнение адиабаты примет вид
| . | (105) |
Учитывая уравнение Майера, возможно утверждать, что показатель адиабаты в любой момент больше единицы. Показатель адиабаты в достаточно широком диапазоне трансформации термодинамических параметров можно считать постоянной величиной, личной для рабочего вещества. В частности, показатель адиабаты для воздуха k=1,4.
Уравнение адиабаты (105) возможно выразить через начальные и конечные значения параметров
| , | (106) |
либо
 . |
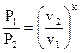(106) |
Уравнение адиабаты может связывать другие пары термодинамических параметров. Эти выражения возможно взять, применяя (106) и уравнение состояния совершенного газа. В итоге получаются следующие соотношения
 , |
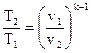(106) |
 . |
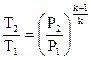(107) |
Чтобы получить выражение для работы в адиабатном ходе, нужно зависимость давления Р от количества v, представленное с учётом (105) и (106) в виде
,
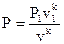Подставить в уравнение (28)
 . |
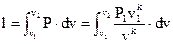(108) |
В следствии интегрирования возможно взять следующие выражения для работы
 . |
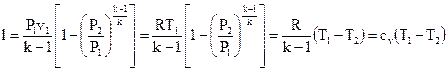(109) |
Последнее равенство возможно конкретно взять из первого закона термодинамики, учитывая, что для адиабатного процесса
,
и, что .
Сравнивая зависимости давления P от количества v в изотермическом 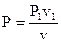и адиабатном процессах 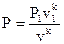, возможно подметить, что преувеличение, изображающая адиабатный процесс, в P-V диаграмме идёт «круче», чем преувеличение изотермы, т.к. k1 (см. рис. 26).
Процесс 1-2a – это процесс адиабатного расширения. Это значит, что работа в этом ходе хороша, а давление и температура, в соответствии с (109), понижаются. Процесс 1-2b – это процесс адиабатного сжатия. Соответственно, давление и температура увеличиваются за счёт подводимой работы.
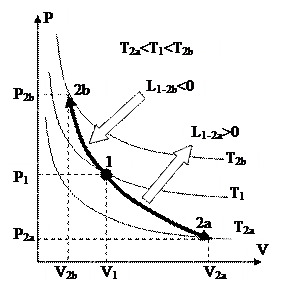
Рис. 26
Для изображения адиабатных процессов в T-S диаграмме нужно их классифицировать.
Адиабатные процессы делиться на 2 типа:
1. изоэнтропные;
2. неизоэнтропные.
Изоэнтропный адиабатный процесс протекает без теплообмена с окружающей средой и без внутреннего тепловыделения, которое может иметь место в совокупности в следствии преодоления сил трения. При наличии в совокупности сил трения на их преодоления требуются затраты работы, которая, в следствии, преобразуется теплоту. В соответствии с (38) эта подводимая к совокупности теплота трения ведет к росту S в совокупности. Исходя из этого, дабы энтропия не возрастала, в совокупности должно отсутствовать трение. Так, адиабатный изоэнтропный процесс – это идеализированные процесс, потому, что в процессах и реальных системах постоянно присутствует трение.
Адиабатный неизоэнтропный процесс протекает без теплообмена с окружающей средой, но с подводом тепла трения, что в любом случае ведет к росту энтропии.
На рис. 27 изображены процесс адиабатного изоэнтропного расширения 1-2a, и процесс адиабатного изоэнтропного сжатия 1-2b. Энтропия в этих процессах не изменяется.
На рис. 28 изображены процесс адиабатного неизоэнтропного расширения 1-2a, и процесс адиабатного неизоэнтропного сжатия 1-2b. Энтропия в этих процессах возрастает.
 |
 |
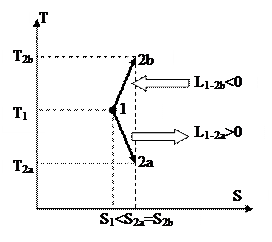Рис. 27. Рис. 28.
Политропный процесс
Термодинамический процесс именуется политропным, если он протекает при постоянной теплоёмкости совокупности, т.е. С=Const.
В этом случае бесконечно малое количество тепла, которым совокупность обменивается с окружающей средой, определяется выражением
| . | (110) |
Уравнение политропного процесса для совершенного газа выводиться на базе 1 — ого уравнения состояния и закона термодинамики совершенного газа
Т.к. , то уравнение 1-ого закона термодинамики получает вид
| . | (111) |
Продифференцировав уравнение состояния совершенного газа, возьмём
| . |
либо
| . |
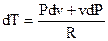(112) |
Учитывая выражение (73), подставим в него (112), а полученный итог – в (111).
В итоге возьмём
 . |
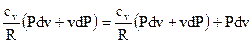Раскрывая скобки в последнем выражении, приводя слагаемые к неспециализированному знаменателю и умножая обе части равенства на R и Собирая слагаемые на базе общности дифференциалов, возьмём
| . |
Учитывая уравнение Майера, возьмём дифференциальное уравнение с разделяющимися переменным
| , |
которое, по окончании разделения переменных принимает вид
 . |
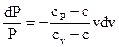Интегрируя последнее уравнение, возьмём
 , |
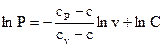где С — произвольная константа.
Избавляясь от логарифмов, это выражение возможно привести к виду
| , | (113) |
которое и есть уравнение политропного процесса для совершенного газа.
Введём в рассмотрение показатель политропы
 . |
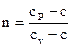(114) |
Тогда уравнение политропы примет вид
| . | (115) |
Из этого выражения видно, что политропный процесс есть обобщением главных термодинамических процессов. В случае, если n=0, то получается уравнение изобарного процесса – P=Const; в случае, если n=?, то возьмём уравнение изохорного процесса V=Const (для этого нужно извлечь корень n – ой степени из обеих частей (115) и учесть что корень нескончаемой степени из любого числа равен 1); в случае, если n=1, то возьмём изотермический процесс Pv=Const; в случае, если n=k — уравнение адиабатного процесса.
Возможно подметить, что по форме уравнение политропы сходится с уравнением адиабаты. Исходя из этого выводы, формально полученные для адиабатного процесса, применимы и для политропного. Т.е. связь между начальными и конечными значениями термодинамических параметров в политропном ходе возможно представить в виде
 , |
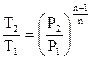(116) |
 , |
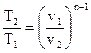(117) |
 . |
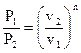(118) |
Выражения для работы в политропном ходе кроме этого подобны уравнениям для работы в адиабатном ходе
 . |
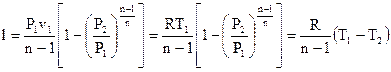(119) |
Из определения показателя политропы n возможно взять выражение для теплоёмкости в политропном ходе
 . |
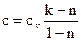(120) |
Из этого уравнения видно, что политропная теплоёмкость возможно как хорошей (nk либо n
Выражение для количества теплоты в политропном ходе имеет форму
| . | (121) |
Это уравнение говорит о том, что в случае, если теплоёмкость хороша, то подвод тепла сопровождается ростом температуры. В случае, если же теплоёмкость отрицательна, то подвод теплоты ведет к уменьшению температуры.
ЛЕКЦИЯ 10
Процесс дросселирования
Дросселированием именуют процесс понижения давления потока при прохождении им через сужение в канале (см. рис. 29). Устройство, реализующее процесс дросселирование, именуется дроссель.
 |
Рис. 29.
Для вывода уравнения процесса дросселирования запишем 1 — ый закон термодинамики для потока с сечениями 1 и 2 (см. рис. 29). Наряду с этим будем вычислять поток горизонтальным, (т.к. расстояние между сечениями 1 и 2 больше диаметра канала), адиабатным, и не делающим технической работы между сечениями 1 и 2, площади которых однообразны, что снабжает равенство скоростей в этих сечениях. Тогда уравнение (80) примет вид
| , |
либо
| . | (122) |
Так, процесс адиабатного дросселирования есть изоэнтальпным процессом.
При дросселировании температура потока может изменяться. Трансформации температуры потока в ходе дросселирования именуется эффектом Джоуля – Томсона.
Эффект Джоуля- Томсона характеризуется коэффициентом адиабатного дросселирования либо дифференциальным дроссель — эффектом
 , |
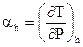(123) |
что будет хорошим , в то время, когда при понижении давления в ходе дросселирования температура потока понижается, ; и дифференциальный дроссель – эффект будет отрицательным , в то время, когда температура с понижением давления возрастает, .
 |
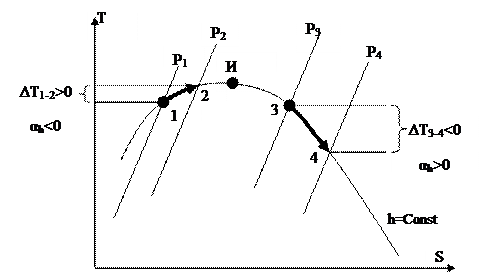Рис. 30.
На рис. 30 изображены четыре изобары ( ), каковые определяют два изоэнтальпных процесса дросселирования 1-2 и 3-4. Процесс 1-2 сопровождается ростом температуры и характеризуется отрицательным дифференциальным дроссель – эффектом . Процесс 3-4 сопровождается понижением температуры и характеризуется хорошим дифференциальным дроссель – эффектом .
Точка, в которой именуется точкой инверсии (точка «И» на рис. 30). Совокупность точек инверсии составляют кривую инверсии, которая всю плоскость диаграммы дробят на две области с хорошим и отрицательным дифференциальным дроссель – эффектом.
Наличие линии инверсии играется значительную роль при выборе рабочего вещества, которое реализует криогенный цикл. Это связано с тем, что процесс дросселирования есть одним из главных процессов понижение температуры установках низкотемпературной техники.
Наличие ненулевого результата Джона –Томсона отмечается у настоящих веществ, отличающихся от совершенного газа. Для совершенного газа калорическое уравнение состояния имеет форму
,
т.е энтальпия не зависит от давления и объёма, а зависит лишь от температуры. Следовательно в случае, если энтальпия при досселировании постоянна, то температура совершенного газа не изменяется, т.е. для него эффект Джоуля – Томсона равен нулю.