Выделим полный квадрат:
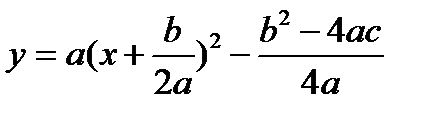
Графиком квадратного трехчлена есть парабола.
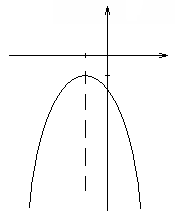
В случае, если 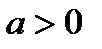 , то ветви параболы направлены вверх, в случае, если
, то ветви параболы направлены вверх, в случае, если 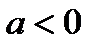 , то вниз.Ось симметрии параболы – прямая
, то вниз.Ось симметрии параболы – прямая 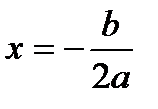 .
.
Вершина параболы 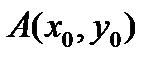 , где
, где 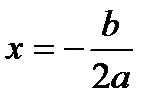 ;
; 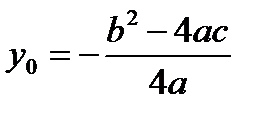 ,
, 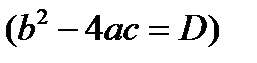
Так: 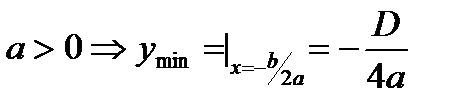
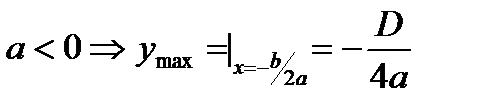
Увидим, в случае, если 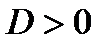 , то корни разные
, то корни разные 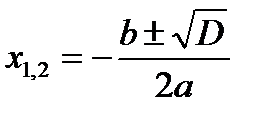
Ось симметрии, 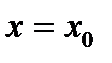 , где
, где 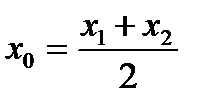 ,
, 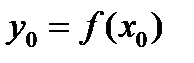
Изучение:
| а0 | а |
| D(f)=R | D(f)=R |
| E(f)=[- ;+?) | E(f)=(-?;- ] |
D0® 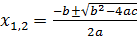 D=0® 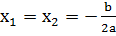 D |
D0® 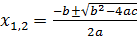 D=0® 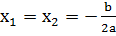 D |
| b=c=0®f(-x)=f(x) в других случаях функция неспециализированного вида | b=c=0®f(-x)=f(x) в других случаях функция неспециализированного вида |
| min y(- )=- | max y(- )=- |
| На промежутке (-?;- ) функция убывает На промежутке (- ;+?) функция возрастает | На промежутке (-?;- ) функция возрастает На промежутке (- ;+?) функция убывает |
Пример 1.
Отыскать параметр С и выстроить график функции:
1. 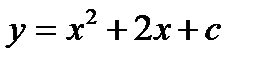 , в случае, если как мы знаем, что ее мельчайшее значение равняется -4.
, в случае, если как мы знаем, что ее мельчайшее значение равняется -4.
2. 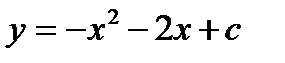 , в случае, если как мы знаем, что ее громаднейшее значение равняется 4
, в случае, если как мы знаем, что ее громаднейшее значение равняется 4
3. 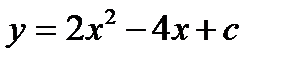 , в случае, если как мы знаем, что ее мельчайшее значение равняется 1
, в случае, если как мы знаем, что ее мельчайшее значение равняется 1
4. 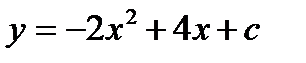 , в случае, если как мы знаем, что ее громаднейшее значение равняется -1
, в случае, если как мы знаем, что ее громаднейшее значение равняется -1
Ответ:
1. 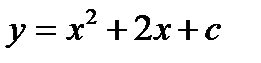
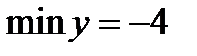
Выделим полный квадрат:
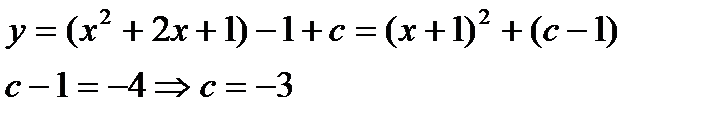
Ответ: 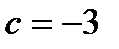
График: 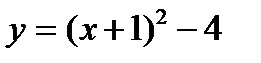
1) 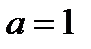
2) ось симметрии: 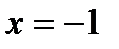
3) вершина параболы: 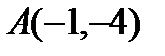
4) 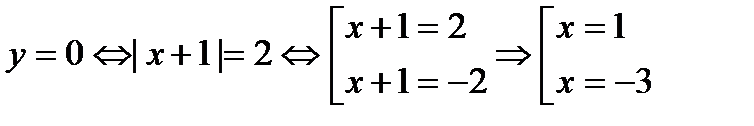
| -3 |
| -1 |
| -4 |
2. 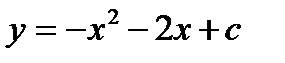
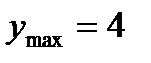
Выделим полный квадрат:
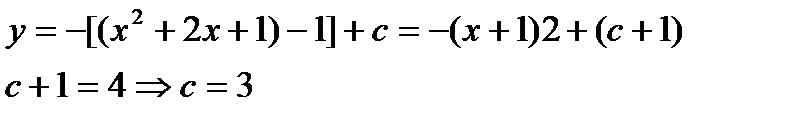
Ответ: 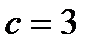
График: 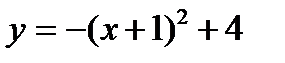
1) 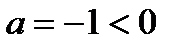
1) ось симметрии 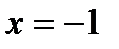
2) вершина параболы: 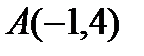
3) 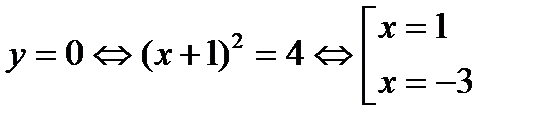
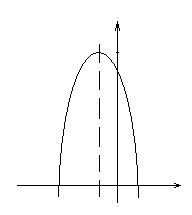
| —3 |
| -1 |
3. 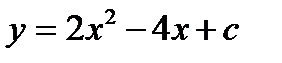
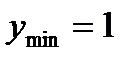
Выделим полный квадрат: 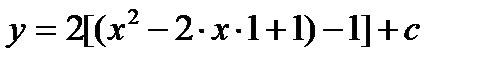
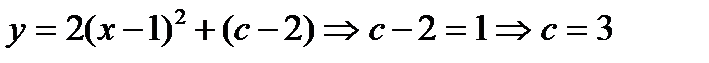
Ответ: 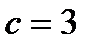
График: 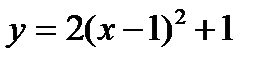
1) 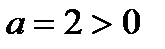
2) ось симметрии 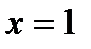
3) вершина 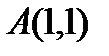
4) 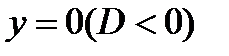 нет точек пересечения с осью OX
нет точек пересечения с осью OX
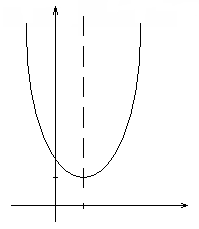
4. 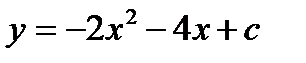
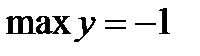
Выделим полный квадрат:
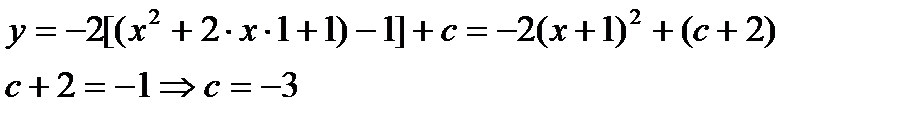
Ответ: 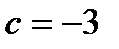
График: 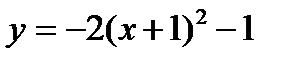
1) 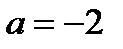
2) ось симметрии: 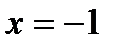
3) вершина: 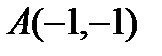
4) 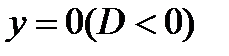 нет точек пересечения с осью ОХ
нет точек пересечения с осью ОХ
| -1 |
| -1 |
Пример 2 (самостоятельно)
Отыскать параметр С и выстроить график функции
1. 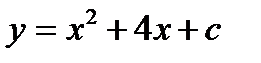 , в случае, если как мы знаем, что ее мельчайшее значение равняется —4
, в случае, если как мы знаем, что ее мельчайшее значение равняется —4
2. 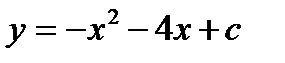 , в случае, если как мы знаем, что ее громаднейшее значение равняется 4
, в случае, если как мы знаем, что ее громаднейшее значение равняется 4
3. 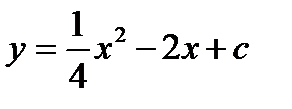 , в случае, если как мы знаем, что ее мельчайшее значение равняется 3
, в случае, если как мы знаем, что ее мельчайшее значение равняется 3
4. 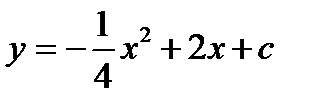 , в случае, если как мы знаем, что ее громаднейшее значение равняется -3
, в случае, если как мы знаем, что ее громаднейшее значение равняется -3
Ответы: 1) 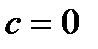 , 2)
, 2) 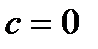 , 3)
, 3) 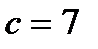 , 4)
, 4) 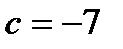
Пример 3.
Выстроить график функции 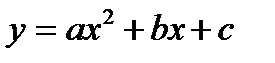 и отыскать:
и отыскать:
- Наименьше значение функции, в случае, если как мы знаем, что:
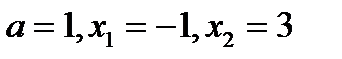
- Громаднейшее значение функции, в случае, если как мы знаем, что:
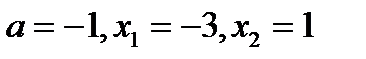
- Наименьше значение функции, в случае, если как мы знаем, что:
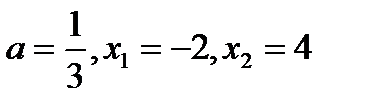
- Громаднейшее значение функции, в случае, если как мы знаем, что:
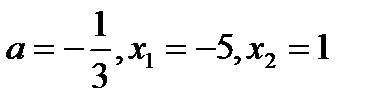
Ответ:
1. 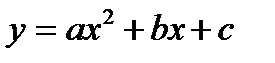
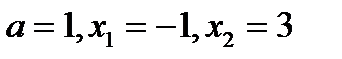
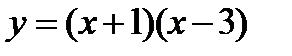
Ось симметрии параболы: 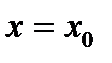 , где
, где 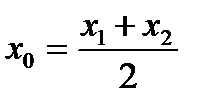 =
= 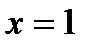
Вершина параболы: 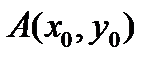 , где
, где 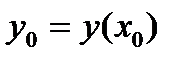
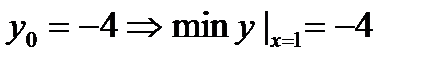
Ответ: miny(1)=-4
График функции: 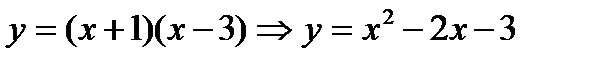
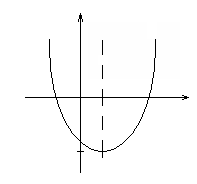
| -4 |
2. 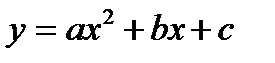
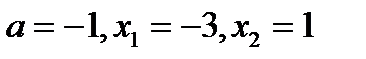
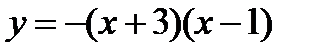
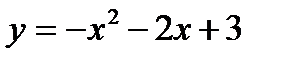
х0= 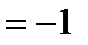
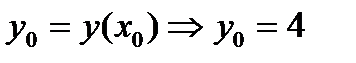
Ось симметрии: 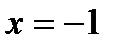
Вершина параболы 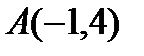
Ответ: 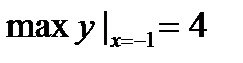
График функции: 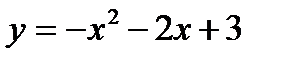
| -1 |
3. 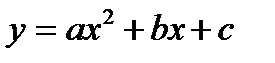
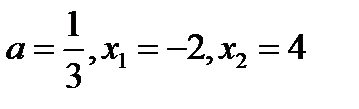
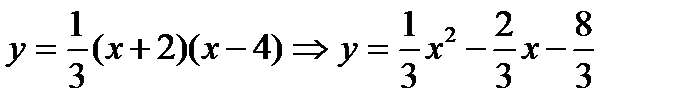
х0= =1 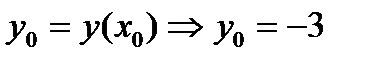
Ось симметрии: 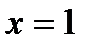
Вершина параболы 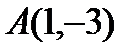
Ответ: 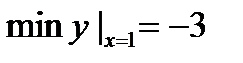
График функции: 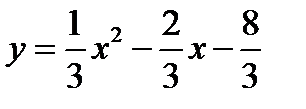
| -3 |
4. 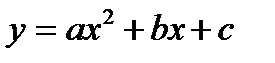
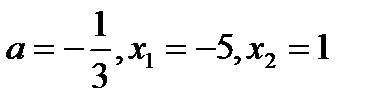
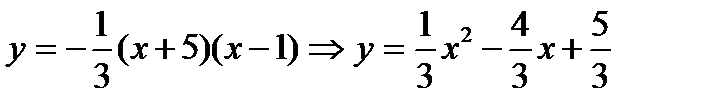
х0= =-2 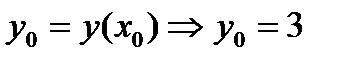
Ось симметрии: 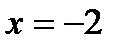
Вершина параболы 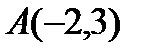
Ответ: 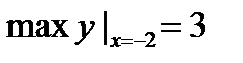
График функции: 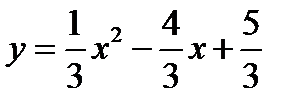
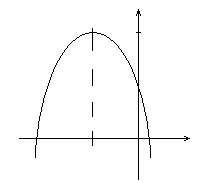
| -2 |
Пример 4.(самостоятельно)
Выстроить график функции 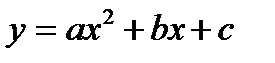 и отыскать:
и отыскать:
- Наименьше значение функции, в случае, если как мы знаем, что:
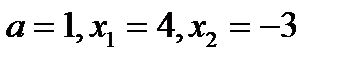
- Громаднейшее значение функции, в случае, если как мы знаем, что:
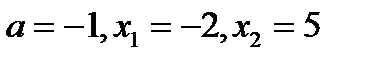
- Наименьше значение функции, в случае, если как мы знаем, что:
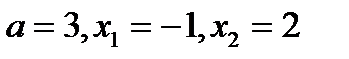
- Громаднейшее значение функции, в случае, если как мы знаем, что:
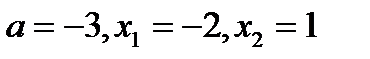
Ответы: 1) 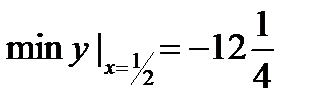 , 2)
, 2) 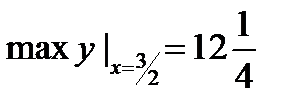 3)
3) 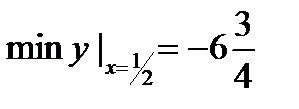 4)
4) 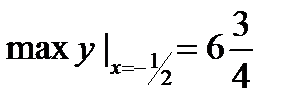
Пример 5.
Определите значение параметра а. Выстройте график функции и отыщите минимальное(большое) значение функции:
1. – ось симметрии параболы
2. – ось симметрии параболы
3. – ось симметрии параболы
4. – ось симметрии параболы
Ответ:
1.
По определению
. Ответ:
Вершина параболы Ответ:
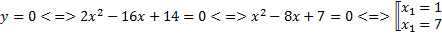
График функции:
| -18 |
2.
Ответ:
Ответ:
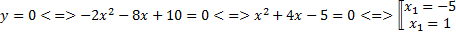
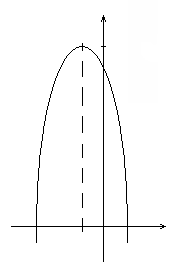 График функции:
График функции:
| -2 |
3.
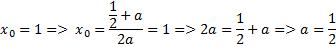
Ответ: 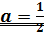
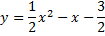
Ответ:
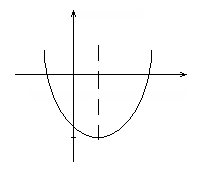 График функции:
График функции:
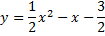
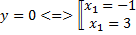
| -12 |
4. – ось симметрии параболы
х0=-1® 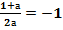 ®а=- ®у=- х2- х+ ,
®а=- ®у=- х2- х+ ,
у0=у(х0)=3® Ответ: max y(-1)=3
Пример 6 (самостоятельно).
Определить значение параметра а. Выстройте график функции и отыщите минимальное (большое) значение функции
1) 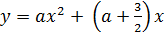 , в случае, если х=-2 – ось симметрии
, в случае, если х=-2 – ось симметрии
2) 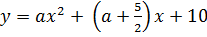 , в случае, если x=2 — ось симметрии
, в случае, если x=2 — ось симметрии
3) 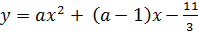 , в случае, если x=-1/3 — ось симметрии
, в случае, если x=-1/3 — ось симметрии
4) 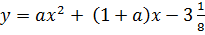 , в случае, если x=-1/4
, в случае, если x=-1/4
Ответы:
1) a=1/2; min y=-2
2) a=-1/2; max y=8
3) a=3; min у=-4
4) a=-2; max y=-3
Пример 7.
Отыскать минимальное (большое) значение функции , в случае, если как мы знаем, что её график проходит через точки:
1) A(0;-3); B(-1;-2); C(2;7);
2) A(-1;-4); B(2;2); C(3;-4);
3) A(2;1); B(1; 4); C(3;4);
4) A(-2,-4); B(-3;-7); C(-4;-16);
Ответ:
В случае, если график проходит через заданные точки, то координаты точек удовлетворяют уравнению.
1) A(0;-3); B(-1;-2); C(2;7);
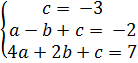 =
= 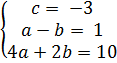 =
= 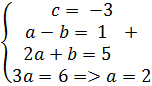
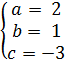
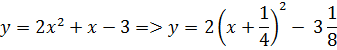
Ответ: 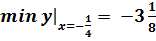
2) A(-1;-4); B(2;2); C(3;-4);
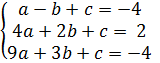 ? =
? = 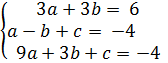 ? =
? = 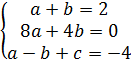 =
=
= 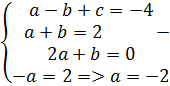 =
= 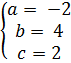 =
=
Ответ:
3) A(2;1); B(1;4); C(3;4);
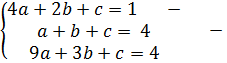 =
= 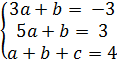 ? =
? = 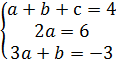 =
=
= 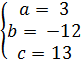 =
=
Ответ:
4) A(-2;-4); B(-3;-7); C(-4;-16);
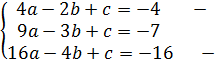 =
= 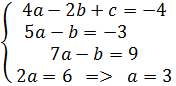 =
= 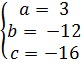
Ответ:
Пример 8.
Отыскать минимальное (большое) значение функции , в случае, если как мы знаем, что её график проходит через точки:
Координаты точек А,В и С задайте самостоятельно.
Пример 9.
Для квадратичной функции на отрезке [?,?] отыскать громаднейшее М и мельчайшее m значение функции. Выстройте график.
1)
2)
3) 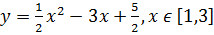
4) 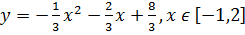
5) 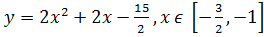
6) 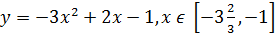
1)
;
Вычислим значение функции на границах промежутка.
Ответ: M=3; m=-1
2)
;
Ответ: M=1; m=-3
3) 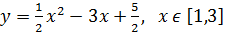
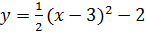 ;
;
Ответ: M=0; m=-2
4) 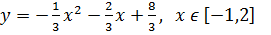
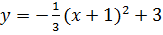 ;
;
Ответ: M=3; m=0
5) 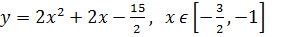
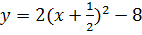 ;
; 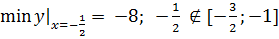
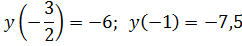
Ответ: M=-6; m=-7,5
6) 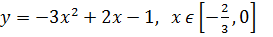
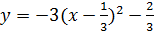 ;
; 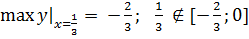
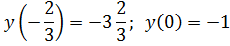
Ответ: M=-1; m 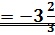
Пример 10.
Задайте самостоятельно интервал и функцию [?,?]. Отыщите мельчайшее и громаднейшее значение функции на этом промежутке.
Пример 11.
Выстройте график функции применяя главные способы преобразований графиков. Отыщите точки экстремумов и множество значений функции
1)
2)
3)
4)
5)
6)
Ответ:
1)
Увидим, что — функция четная, и по условию
Делаем последовательно построение графиков следующих функций:
А) либо
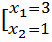
Б) симметричное дополнение графику (А) относительно оси OY.
В) — искомая функция.
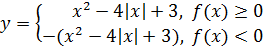 Рис.1
Рис.1
| -1 |
| -3 |
| 3 |
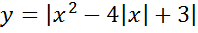
Рис.1
Ответ: Точки экстремумов
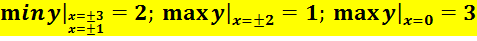
2)
Увидим, что
Будем строить график функции помощью преобразований графиков.
А)
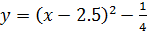
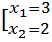 ;
;
Б)
В)
Рис.2
| -3 |
| -2 |
| 2.5 |
| 1/4 |
| -1/4 |
Рис.2
Ответ: Точки экстремумов
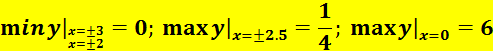
3)
Раскроем символ модуля
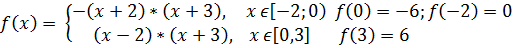
Рис.3
| -6 |
| -2 |
рис. 3
Ответ: Точки экстремумов
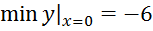
4)
Раскроем символ модуля на данном промежутке:
| -4 |
| -1 |
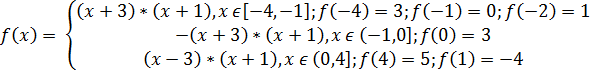
| -1 |
| —1 |
| -2 |
| -3 |
| -4 |
| -3 |
| -4 |
Рис.5
| -7 |
| -7 |
| -7 |
| -7 |
| -7 |
| -7 |
| -7 |
| -7 |
| -7 |
| -7 |
| -7 |
Рис.5
Ответ: Точки экстремумов
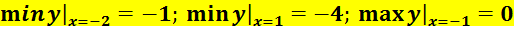
Пример 12.
Выстроить график функции y = f(x), применяя главные способы преобразований графиков. Отыщите множества значений и точки экстремумов функции E(f).
1) 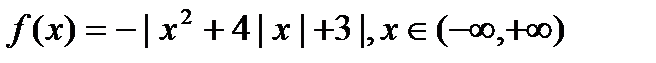
2) 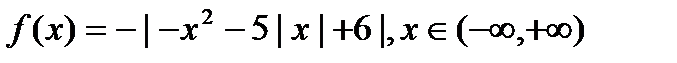
3) 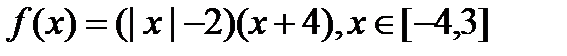
4) 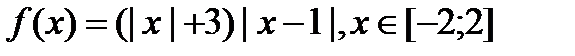
Ответы: 1) 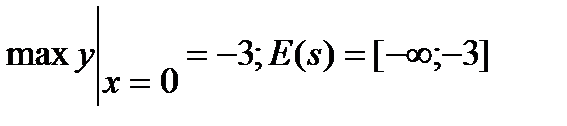
2) 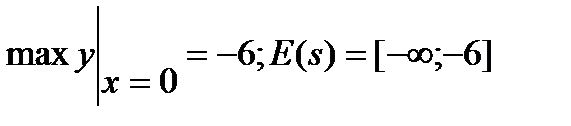
3) 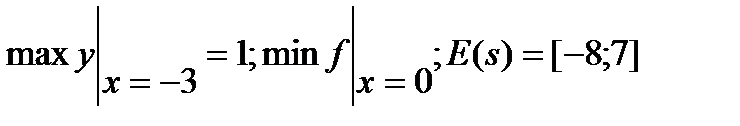
4) 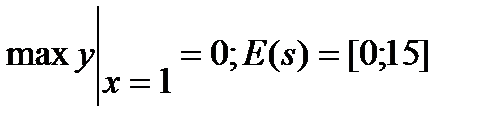
Показательная функция.
Функция вида:
у= , а0; а?1