17/36
Кинуты две игральные кости. Отыскать возможность того, что произведение выпавших чисел равно три?
5/9
Кинуты три игральные кости. Отыскать возможность того, что все выпавшие числа разны?
5/9
Кинуты три игральные кости. Отыскать возможность того, что все выпавшие числа разны?
5/9
В
Вычислить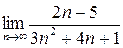 
Вычислить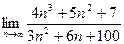 
?
Вычислить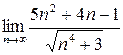 
Вычислить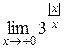 
Вычислить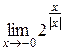 
Вычислить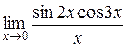 
Вычислить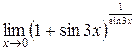 
e
Вычислить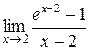 
Вычислить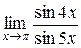 
4/5
Вычислить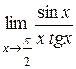 
Вычислить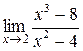 
Вычислить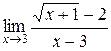 
1/4
Вычислить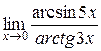 
5/3
Вычислить
Вычислить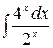 
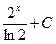
Вычислить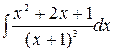 
ln|x+1|+C
Вычислить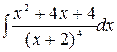 
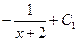
Вычислить
Вычислить
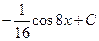
Вычислить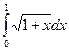 
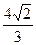
Вычислить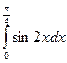 
1/2
Вычислить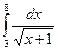 
Вычислить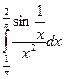 
Вычислить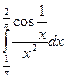 
-1
Вычислить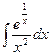 
Вычислить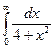 
?/4
Вычислить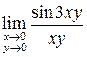 
В точке – точке вероятного экстремума два раза дифференцируемой функции нет экстремума, в случае, если:
АС-B2
В коробке имеется 10 подробностей, среди которых 4 окрашенных. Сборщик наудачу извлекает три подробности. Отыскать возможность того, что хотя бы одна окрашенная подробность.
5/6
В коробке 10 белых, 15 тёмных, 10 желтых и 25 красных шаров. Отыскать возможность того, что наудачу забранный шар белый.
либо 1/6
В коробке имеется 10 белых, 15 тёмных, 10 желтых и 25 красных шаров. Отыскать возможность того, что наудачу забранный шар нечерный.
45/60=3/4
В коробке имеется 10 белых, 15 тёмных, 10 желтых, и 25 красных шаров. Наудачу забрали два шара. Отыскать возможность того, что оба шара желтые либо белые.
3/59
Возможность точного события равна:
Возможность неосуществимого события равна:
Возможность любого события имеется положительное число, удовлетворяющее неравенству:
0?P(A)?1
Возможность появления одного из двух несовместных событий, безразлично какого именно, равна:
P(A+B)=P(A)+P(B)
Возможности противоположных событий и удовлетворяют условию:
Возможность совместного появления двух зависимых событий равна:
P(AB)=P(A)?PA(B)
Возможность появления хотя бы одного из двух совместных событий и
P(A+B)=P(A)+P(B)-P(AB)
Возможность выпадения события в каждом из 20 свободных событий равна 0,4. Отыскать математическое ожидание?
В урне 4 белых и 2 тёмных шара. Случайным образом извлечены два шара. Отыскать возможность того, что шары разного цвета?
8/15
В учебной группе 12-студентов, из которых 8-отличников. Случайным образом отобраны 9 студентов. Отыскать возможность того, что среди отобранных студентов пятеро отличников?
11/55
Выборочное среднее квадратическое отклонение выборки определяется формулой:
Г
Градиентом функции в данной точке именуется вектор, координаты которого равны соответственно
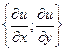
Градиентом функции в данной точке есть вектор, координаты которого равны
(5;2)
Градиентом функции в данной точке есть вектор, координаты которого равны
(2;2)
Градиентом функции в данной точке есть вектор, координаты которого равны
(3;-1)
Градиентом функции в данной точке есть вектор, координаты которого равны
(-3;2)
Градиентом функции в точке есть:
grad z={5;-1}
Д
Дан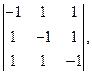 
отыскать
Дан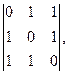 
отыскать
-1
Разрешена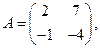 
найти
-1
Разрешено: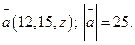 
Найти третью координату вектора, в случае, если как мы знаем, что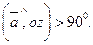 
-16
Даны точки и . Отыскать
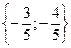
Даны векторы и Отыскать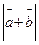 
Даны векторы и Отыскать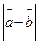 
Даны векторы и Отыскать
Даны векторы и Отыскать
1/5
Дана прямая . Угловой коэффициент параллельной ей прямой равен
k=5/6
Дана прямая . Угловой коэффициент перпендикулятной ей прямой равен
k=-3/5
Для каких функций отрезок есть областью определения 1) 2)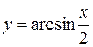 
3)
y=arccosx
Для каких функций вся числовая ось есть областью определения 1) 2) 3)
y=tg3x
Достаточным показателем локального экстремума функции в точке М (нужное условие экстремума выполняется) есть условие:
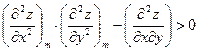либо
Дисперсией дискретной случайной размеры именуют
D(x)=M[x-M(x)]2
Дисперсия постоянной величины равна
D(C)=0
Дисперсия числа появлений события в свободных опробованиях, в каждом из которых возможность появления события постоянна, равна
D(x)=npq
Для событий и правильно равенство:
Для двух зависимых событий А и В правильно равенство:
P(A?B)=P(A)?PA(B)
Для случайной величины математическое ожидание . Отыскать
M(x?2)=2?M(x)=4
Дисперсия суммы двух свободных случайных размеров равна
D(x+y)=D(x)+D(y)
Дисперсия разности двух свободных случайных размеров равна
D(x-y)=D(x)+D(y)
Дан дискретный статистический последовательность
Выяснить выборочное среднее
Дан дискретный статистический последовательность
Выяснить выборочную дисперсию
3,2
Дан дискретный статистический последовательность
Отыскать среднее квадратическое отклонение
1,79
Дан дискретный статистический последовательность
Отыскать медиану вариационного последовательности
3,5
Дана выборка
| Вариант | ||||
| Частота |
Отыскать среднюю выборочную:
Е
В случае, если точка – точка вероятного экстремума два раза дифференцируемой функции , то она есть точкой максимума при условиях:
В случае, если точка – точка вероятного экстремума два раза дифференцируемой функции , то она есть точкой минимума при условиях:
В случае, если степенной последовательность сходится, в точке , то
-x0
В случае, если степенной последовательность расходится в точке , то
xx0, x
В случае, если последовательность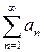 
сходится, то последовательность 
?
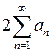сход.
В случае, если последовательность 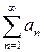и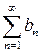 
сходятся, то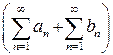 
сход.
В случае, если последовательность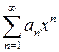 
сходится в точке то последовательность
|x0|
В случае, если знако переменный последовательность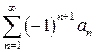 
сходится и сумма равна , то
S
В случае, если число всех единственно вероятных и равновозможных элементарных финалов опробования, а число помогающих событию финалов, то возможность события определяется формулой:
P(A)=m/n
З
Записать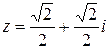 
в тригонометрической форме
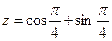
Записать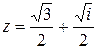 
в показательной форме
Значение личной производной функции по доводу в точке равняется:
Значение личной производной функции по доводу в точке равняется:
Значение личной производной функции по доводу в точке равняется:
Значение личной производной функции по доводу в точке равняется:
Значение личной производной функции по доводу в точке равняется:
Значение личной производной функции по доводу в точке равняется:
Значение личной производной функции по доводу в точке равняется:
Значение личной производной функции по доводу в точке равняется:
Значение личной производной второго порядка функции в точке равняется:
Значение личной производной второго порядка функции в точке равняется:
Значение личной производной второго порядка функции
в точке равняется:
Значение личной производной второго порядка функции в точке равняется:
Значение личной производной второго порядка функции в точке равняется:
Значение личной производной второго порядка функции в точке равняется:
Значение личной производной второго порядка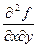 
функции в точке равняется:
Значение личной производной второго порядка 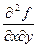функции в точке равняется:
Значение личной производной второго порядка 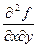функции в точке равняется:
Значение личной производной функции по доводу в точке равняется:
Заданы случайные размеры,
| Х | У | ||||
| Р | 0,4 | 0,6 | Р | 0,2 | 0,8 |
тогда математическое ожидание равняется:
M(x)=2,2 M(y)=3,6 M(x+y)=5,8
И
Интеграл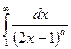 
сходится, в случае, если
a0 либо a1
Интеграл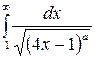 
сходится, в случае, если
a2
Известно следующее свойство градиента: градиент функции показывает направление
громаднейшего по возрастанию
Изучить на сходимость последовательность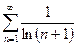 
расход
Изучить на сходимость последовательность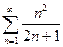 
расх
Изучить на сходимость последовательность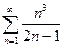 
расх
Изучить на сходимость последовательность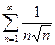 
сход
Изучить сходимость последовательности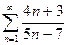 
расход
Изучить сходимость последовательности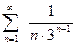 
сход
Изучить на сходимость последовательность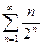 
сход
Изучить сходимость последовательности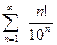 
расход
Изучить сходимость последовательности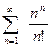 
расх
Изучить на сходимость последовательность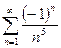 
сход. полностью
Изучить на сходимость последовательность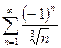 
сход. условно
Изучить на сходимость последовательность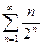
сход.
Изучить на сходимость последовательность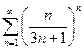 
сход.
Изучить на сходимость последовательность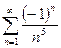
сход. полностью
Изучить на сходимость последовательность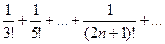 
сход.
Из главной совокупности извлечена выборка количества n=60:
| Варианта | ||||
| Частота |
Отыщите выборочную среднюю
Исправленной выборочной дисперсией именуется величина:
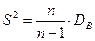
К
Какие конкретно из следующих функций постоянны в точке 1)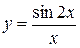 
, 2) 
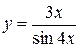, 3)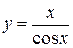 
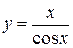
Какие конкретно из следующих функций постоянны в точке 1)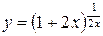 
, 2) 
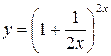, 3)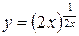 
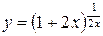
Какие конкретно функции являются вечно малыми одного порядка при 1) , 2) , 3) , 4)
,
Какие конкретно функции являются вечно малыми одного порядка при 1)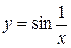 
, 2) 
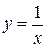, 3)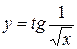 
,
,
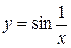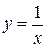
Каким возможно промежуток сходимости последовательности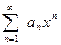 
(-R;R)-любой
Каким возможно промежуток сходимости последовательности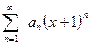 
-R-1
Какая из формул есть формулой Байеса?
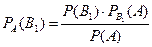
Какая из формул есть формулой Бернулли?
Какое из этих равенств правильно для интегральной функции распределения возможностей случайной величины?
Л
Линией уровня функции именуется множество таких точек , для которых функция принимает:
f(x;y)=c постоянное значение
М
Монотонно возрастающими на всей числовой оси среди функций 1) . 2) , 3) являются
Математическое ожидание биномиального распределения равняется
M(x)=n?p
Математическое ожидание постоянной случайной величины , вероятные значения которой принадлежат всей оси , определяется равенством
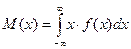
Монета кинута пять раз. Отыскать возможность того, что «герб» выпал два раза
5/16
Монета кинута пять раз. Отыскать возможность выпадения «герба» четыре раза
5/32
Математическое ожидание суммы двух случайных размеров M(X+Y) равняется:
M(x+y)=M(x)+M(y)
Математическое ожидание произведения двух свободных случайных размеров равняется
M(x?y)=M(x)?M(y)
Математическое ожидание отклонения (X-M(X)) равняется
Модой вариационного последовательности именуется:
вариант имеющий громаднейшую частоту
Медианой вариационного последовательности именуется: