Неоднородная краевая задача.
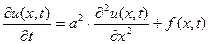. (1)
,
где:
u(x,t) – температура стержня;
х – пространственная переменная;
a2 – коэффициент температуропроводности;
f(x,t) – внешнее действие.
Начальные условия:
; (2)
;
Граничные условия:
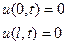(3)
Будем искать ответ данной задачи в виде последовательности Фурье по собственным функциям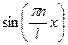 
вида:
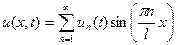. (4)
Представим функцию кроме этого в виде последовательности Фурье по данной ортогональной совокупности:
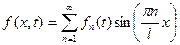. (5)
где:
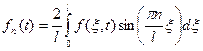. (6)
Выражения (4), (5) подставим в уравнение (1), будем иметь:
.
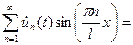
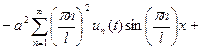
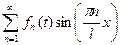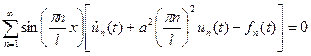. (7)
направляться обратить внимание на то, что последовательность (7) будет равен нулю, в случае, если все коэффициенты этого последовательности будут равны нулю, поскольку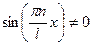 
. Тогда с учетом этого запишем:
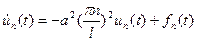. (8)
Взяли неоднородное дифференциальное уравнение первого порядка с постоянными коэффициентами.
Отыщем начальные условия для уравнения (8) на базе соотношений (2),(4).
. (9)
Будем решать уравнения (8), (9):
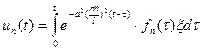. (10)
Подставим (10) в (4), возьмём:
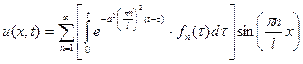. (11)
Преобразуем (11) с учетом (6), будем иметь:
.
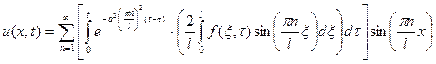Либо
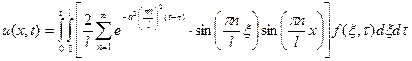. (12)
Запишем функцию мгновенного точечного источника:
.
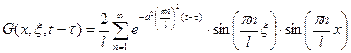Приведем решение:
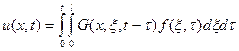. (13)
Функция G является распределением температуры в стержне в момент времени, в случае, если температура в начальный момент времени ( ) равнялась нулю и в момент времени в точке выделяется некое количество тепла в виде — импульса и наряду с этим на краях поддерживается нулевая температура.
Запишем следующее:
. (14)
В случае, если подставить (14) в (13) будем иметь:
.
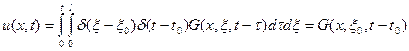Неспециализированная краевая задача.
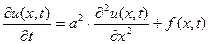, (1)
.
Начальные условия:
. (2)
Граничные условия:
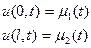. (3)
Введем в рассмотрение выражение вида:
. (4)
где — главная функция;
— запасной функция.
Подставим (4) в (1), будем иметь:
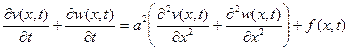. (5)
Совершим следующие преобразования с (5):
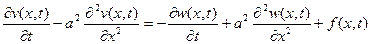. (6)
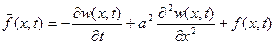. (7)
. (
Так, функция определяется уравнением (8), которое будем разглядывать при граничных условиях, взятых на основании (2-4).
Выразим из (4) :
. (9)
Имея начальные условия (2), запишем:
. (10)
Кроме этого на основании (3) возможно записать:
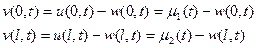(11)
Выберем запасного функцию так, дабы:
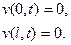
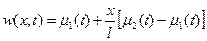(12)
Итак, нахождение функции связано с нахождением функции , которая находится как ответ краевой задачи при нулевых граничных условиях. Способ ее нахождения нами был рассмотрен ранее.
В случае, если начальные условия ненулевые, то к этому ответу нужно прибавить ответ однородного уравнения при ненулевых начальных условиях (это справедливо для всех задач, разглядываемых в этом курсе).
Приведем рассмотренные виды задач и соответствующие им решения:
Однородная краевая задача
.
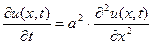Начальные условия:
.
Граничные условия:
.
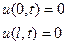Ответ:
.
Неоднородная краевая задача
.
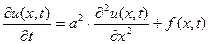Начальные условия:
.
Граничные условия:
.
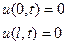Ответ:
.
При ответ примет вид:
.
Неспециализированная краевая задача
.
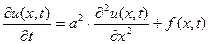Начальные условия:
.
Граничные условия:
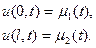
Метод ответа:
1. .
2. 
.
.
.
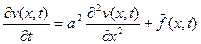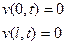Находится ответ:
.
3. 
.
.
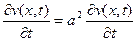Находится ответ:
.
4. .
5. .
Получено ответ неоднородной и неспециализированной краевой задачи. Неспециализированная краевая задача решается как неоднородная краевая задача при нулевых начальных условиях.
Лекция 6.
Применение интегрального преобразования Лапласа
Для анализа СРП.
Главные понятия.
Способ преобразования Лапласа пребывает в том, что изучается не сама функция (оригинал), а её видоизменение (изображение). Это видоизменение – преобразование – производится при помощи умножения на некую интегрирования и экспоненциальную функцию в определенных пределах.
Пускай изучаемая функция имеется кусочно-постоянная функция вещественной переменной . Кусочно-постоянной функцией именуют однозначную функцию, имеющую в конечном промежутке ( ) конечное число разрывов непрерывности в точках . В каждом промежутке ( ) функция постоянна, причем она стремиться к конечному пределу при приближении к границе.
Функцию именуют оригиналом функции.
Преобразование Лапласа функции будет пребывать в умножении её на и интегрировании в пределах от 0 до :
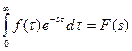(1)
где — некая комплексная величина. В следствии интегрирования возьмём некую функцию , которая именуется преобразованной функцией по Лапласу, либо изображением функции.
Так, преобразование Лапласа есть интегральным преобразованием; это преобразование изображается знаком :
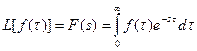(2)
Причем изображение существует, в случае, если интеграл (1) сходиться.
Для упрощения главных соотношений ограничим класс разглядываемых функций. Функцию принимают кусочно-постоянной и хорошей от 0 лишь при . Величина обозначает в будущем , а равна нулю. Потом из класса кучно-постоянных функций выделяем под класс функций, характеризуемых тем, что асимптотические значения функции при меньше асимптотического значения функции , где , т. е. при большом :
(3)
либо
(4)
где — некое конечное положительное число.
При указанных ограничениях, накладываемых на функцию , интеграл (1) есть регулярной функцией от s в правой полуплоскости от прямой , т. е. функция имеет производные всех порядков в указанной области и все её особенные точки находятся в комплексной плоскости от прямой .
Условимся оригинал функции обозначать строчными буквами, а её изображение — прописными буквами., к примеру: — оригинал функции, а — изображение, тогда:
(5)
Нужно подчернуть, что не любая функция имеет изображение. К примеру, не существует оригинала для функции , так как полюсы данной функции расположены на всей вещественной оси , а не слева от прямой . Но возможно продемонстрировать, в случае, если Ф(s) есть изображением , то соответствующий оригинал будет единственным, что являлся бы кусочно-постоянной функцией.
В случае, если функция растет стремительнее, чем , то для нее существует изображения. К примеру функция не имеет изображения, поскольку для нее интеграл Лапласа расходиться. Но, к примеру, разрывная функция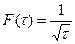 
(она стремиться к бесконечности, в то время, когда ) имеет изображение 
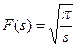, так как интеграл Лапласа сходиться.
Функция возможно ступенчатой; к примеру,
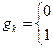
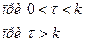(6)
Изображение её следующее
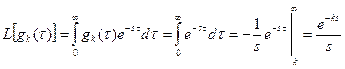(7)
Свойства преобразования Лапласа
Свойство линейности. Преобразование Лапласа есть линейным, т. е. в случае, если А и В – постоянные, то по определению преобразованию Лапласа возможно написать:
(8)
где и — соответственно изображения функций и .
Пользуясь этими свойством возможно отыскать изображения последовательности функций.
Изображение производной. Пускай . Отыщем ,
где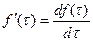 
.
(9)
По большому счету
(10)
Так, для функции с указанным асимптотическим поведением при условии существования постоянных ее производных впредь до существует изображение для производной .
Интегрирование оригинала функции. Отыщем изображение функции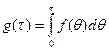 
, т. е. отыщем
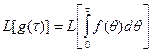(11)
Так как , то
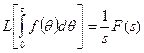(12)
Так, интегрирование оригинала функции соответствует делению изображения на величину , т. е. величина владеет свойством оператора интегрирования.
Обратное преобразование Лапласа. Знак обозначал преобразование функции , т. е. по оригиналу функции находим ее изображение. Это воздействие именуют прямым преобразованием Лапласа. Во многих задачах нужно отыскать оригиналы функции по её изображению . Условились знаком обозначать обратное преобразование Лапласа, которое должно обозначать искомую функцию, т.е. оригинал функции.
, (13)
То обратное преобразование должно давать оригинал функции
. (14)
К примеру,
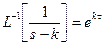; (14)
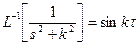. (15)
Более строгое рассмотрение вопроса ведет к заключению, что обратное преобразование Лапласа в общем случае не есть оригинал функции и лишь при известных условиях дает оригинал функции. К примеру, обратное преобразование функции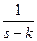 
равняется , так как прямое преобразование даст изображение 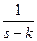, но возможно отыскать и другую функцию :
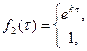
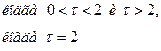(16)
которая дает также изображение. Нужно подчернуть, что имеет разрыв непрерывности при . Отыскать вторую постоянную функцию для заданного изображения запрещено. Исходя из этого заданное изображение функции не имеет возможности иметь больше одного оригинала функции , постоянной для каждого значения . В большинстве разглядываемых задач математической физики обратное преобразование есть однозначным.
Обратное преобразование есть линейным, что вытекает из соотношения (1), т.е.
. (18)
Способ ответа несложных дифференциальных уравнений
Пользуясь фундаментальными особенностями преобразования Лапласа, возможно решать несложные дифференциальные уравнения.
Способ ответа складывается из следующих трех этапов.
1. К дифференциальному уравнению используем преобразование Лапласа и вместо дифференциального уравнения для оригинала функции приобретаем уравнение для изображения функции.
Так как преобразование Лапласа есть интегральным преобразованием и владеет особенностями операторов, то вместо дифференциального уравнения для оригинала функции приобретаем алгебраическое уравнение относительно изображения.
2. Полученное алгебраическое уравнение решается относительно изображения функции, причем s рассматривается как число. Следовательно, второй этап сводиться к нахождению ответа для изображения функции.
3. При помощи известных соотношений между изображением её и функции оригиналом пребывать ответ для оригинала функции, т.е. оригинал искомой функции.
Так, в начале используется прямое преобразование, а после этого обратное. Преимущество этого способа пребывает в том, что решается не дифференциальное уравнение для оригинала функции, а алгебраическое уравнение для изображения.
Лекция 7.
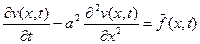