Повторные свободные опробования.
На практике довольно часто приходится сталкиваться с задачами, каковые возможно представить в виде многократно повторяющихся опробований при данном комплексе условий, в которых воображает интерес возможность числа m наступлений некоего события А в n опробованиях. В случае, если возможность наступления события А в каждом опробовании не изменяется в зависимости от финалов вторых, то такие опробования именуются свободными относительно события А. В случае, если свободные повторные опробования проводятся при одном и том же комплексе условий, то возможность наступления события А в каждом опробовании одинаковая. Такая последовательность свободных опробований стала называться схемы Бернулли (Якоб Бернулли швейцарский математик 1654 – 1705).
Формула Бернулли.
Теорема. В случае, если возможность p наступления события А в каждом опробовании постоянна, то возможность того, что событие А наступит m раз в n свободных опробованиях, равна
, где q=1-p
Следствия:
1. (возможность того, что событие А не случится ни разу).
2. (возможность того, что событие А случится n раз).
3. (возможность того, что событие А случится лишь один раз).
4. (возможность того, что событие А случится хотя бы один раз).
Наивероятнейшее число
Число наступления события А в n свободных опробованиях именуется наивероятнейшим, в случае, если по крайней мере не меньше возможности вторых событий при любом m, другими словами . Возможно продемонстрировать, что:
Пример: Возможность изготовления на автоматическом станке стандартной подробности равна 0,8. Отыскать наивероятнейшее число появления бракованных подробностей из 5 отобранных и возможность этого числа.
Пускай событие А- изготовление бракованной подробности. P(A)=1-0,8=0,2=p, q=0,8, n=5
5•0,2-0,8? 5•0,2+0,2 0,2? 1,2 =
Замечание: В случае, если m и n громадны, p мало, то вычисление по формуле Бернулли будет затруднительно. В этом случае используют приближенные, так именуемые асимптотические формулы.
Формула Пуассона.
(Пуассон Симеон Дени французский математик 1781-1840)
В случае, если возможность p наступления события А в каждом опробовании пытается к нулю (p0) при неограниченном повышении числа опробований (n?), причем произведение np пытается к постоянному числу ? (np?), то возможность того, что событие А покажется m раз в n свободных опробованиях, приближенно равна:
, где ?=np
Функция — функция Пуассона. Для нахождения значений данной функции существуют особые таблицы для разных m и ?.
Замечание: формула Пуассона используется, в то время, когда npq?10.
Пример:
На факультете насчитывается 1825 студентов. Какова возможность того, что 1сентября есть днем рождения четверых студентов?
n=1825 , m=4 , какое количество= , ?=np=1825•
Применим приближенную формулу Пуассона:
0.1755 (нашли по таблице)
Локальная формула Муавра – Лапласа.
(Муавр Абрахам де британский математик, француз по национальности, 1667-1754; Лаплас Пьер Симон французский математик 1749-1827; формулы взяты Муавром в 1718г. для p= q= , неспециализированный случай рассмотрен Лапласом в 1812г.)
В случае, если m и n громадны, но число m-np ограничено, npq ?10, то используем приближенную формулу для вычисления возможности появления события А m раз в n свободных опробованиях:
,
где 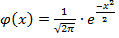
Для упрощения расчетов составлена таблица значений функции . Пользуясь данной таблицей, нужно учитывать свойства функции
1) — четная функция = ;
2) .
Пример:
Имеется партия резисторов из 10000 штук. Какова возможность того, что в данной партии бракованных резисторов 20 штук, в случае, если возможность брака 0,001.
n=10000 , m=20, p=0,001 , q=1-p=0,999
Замечание:
Время от времени требуется отыскать возможность наступления события А в n опробованиях от до раз. В случае, если разность не громадна, то возможно воспользоваться прошлыми формулами и применить теорему сложения.
В случае, если разность большая, то указанные формулы приводят к затруднительному ответу. В этом случае применяют интегральную формулу Муавра – Лапласа.