Довольно часто нам нужно создать отчет для различных типов данных, например, проанализировать лишь конкретные округи. Вместо того, дабы тратить время на трансформации данных, воспользуемся областью фильтры. Перетащите полеФедеральный округ в область Фильтры. Сейчас вы имеете возможность поменять внешний вид сводной таблицы, задав фильтр на нужном округе.
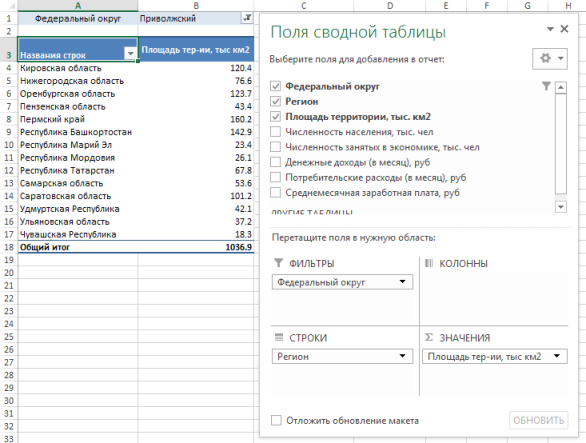
Обновление сводной таблицы
Со временем данные изменяются, к ним добавляются колонки и новые строки. Для обновления сводной таблицы выпользуйте командой Обновить, для этого щёлкните правой кнопкой мыши на любом месте таблицы и выберите Обновить.
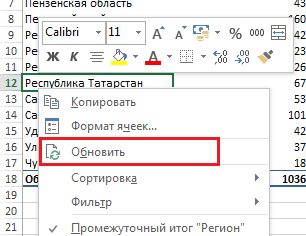
Бывают обстановке, в то время, когда структура данных изменяется, например, вам нужно добавить новые строчка в таблицу с данными. Данный тип трансформаций повлияет на диапазон источника данных, и об этом нужно сказать сводной таблице. Простое обновление не сработает, в этом случае нужно увеличить диапазон источника данных.
Щелкаем левой кнопкой мыши в любом месте сводной таблицы. Идем во вкладку Работа со сводными таблицами — Анализ – Источник данных.
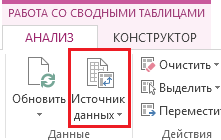
В показавшемся диалоговом окне Поменять источник данных сводной таблицызадаем изменившийся диапазон данных.
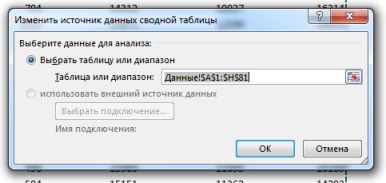
Функции MS EXCEL: логические, статистические временные, текстовые математические.
Логические функции Excel
одобного рода функциями помогают такие, каковые возвращают итог по окончании проверки данных, что постоянно представляет «ИСТИНА» или «Неправда», что свидетельствует – итог удовлетворяет заданному условию или не удовлетворяет, соответственно.
Перед тем как перейти к рассмотрению обрисованных функций, ознакомьтесь со статьей отечественного сайтаУсловия строк и сравнения чисел в Excel.
В описаниях синтаксиса функций их доводы, каковые заключены в квадратные скобки «[]», являются необязательными.
Будут рассмотрены следующие функции:
- ИСТИНА;
- Неправда;
- И;
- Либо;
- НЕ;
- В случае, если;
- ЕСЛИОШИБКА.
Функция ИСТИНА
Не принимает никаких доводов и просто возвращает логическое значение «ИСТИНА».
Синтаксис: =ИСТИНА()
Функция Неправда
Подобна функции ИСТИНА, за исключением то, что возвращает противоположный итог Неправда.
Синтаксис: =Неправда()
Функция И
Возвращает логическое значение ИСТИНА, в случае, если все доводы функции вернули подлинное значение. В случае, если хотя бы один довод возвращает значение Неправда, то вся функция вернет данное значение.
В виде доводов должны приниматься условия или ссылки на ячейки, возвращающие логические значения. Количество доводов не имеет возможности быть больше 255. Первый довод есть необходимым.
Разглядим таблицу истинности данной функции:
| И | ИСТИНА | Неправда |
| ИСТИНА | ИСТИНА | Неправда |
| Неправда | Неправда | Неправда |
Синтаксис: =И(Логическое_значение1; [Логическое_значение1];…)
Пример применения:
В первом примере видно, что все доводы возвращают подлинное значение, следовательно, и сама функция вернет подлинный итог.
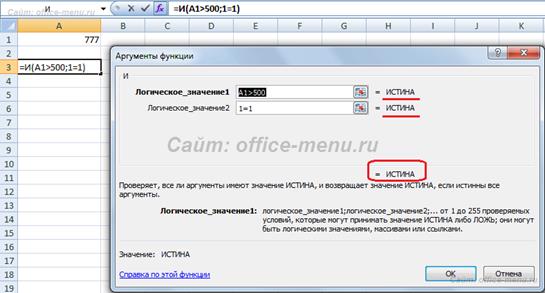
Во втором примере функция ни при каких обстоятельствах не вернет значение ИСТИНА, т.к. условие ее второго довода заблаговременно неравно.
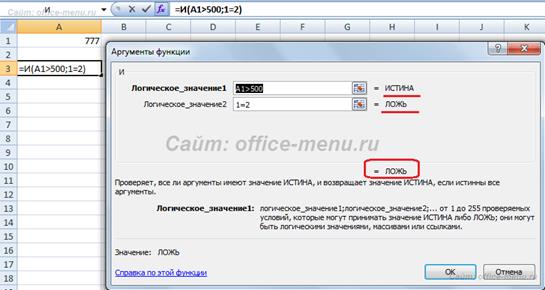
Функция Либо
Возвращает логическое значение ИСТИНА, в случае, если хотя бы один довод функции вернет подлинное значение.
В виде доводов принимаются условия или ссылки на ячейки, возвращающие логические значения. Количество доводов не имеет возможности быть больше 255. Первый довод есть необходимым.
Таблица истинности функции Либо:
| Либо | ИСТИНА | Неправда |
| ИСТИНА | ИСТИНА | ИСТИНА |
| Неправда | ИСТИНА | Неправда |
Синтаксис: =Либо(Логическое_значение1; [Логическое_значение2];…)
Как пример, разглядите примеры функции И, все они вернут итог ИСТИНА, т.к. первый довод есть подлинным.
Функция НЕ
Принимает в виде довода всего одно логическое значение и меняет его на противоположное, т.е. значение ИСТИНА она поменяет на Неправда и напротив.
Таблица истинности функции И с применением функции НЕ:
| НЕ(И()) | ИСТИНА | Неправда |
| ИСТИНА | Неправда | ИСТИНА |
| Неправда | ИСТИНА | ИСТИНА |
Таблица истинности функции Либо с применением функции НЕ:
| НЕ(Либо()) | ИСТИНА | Неправда |
| ИСТИНА | Неправда | Неправда |
| Неправда | Неправда | ИСТИНА |
Синтаксис: =НЕ(логическое_значение)
Функция В случае, если
есть одной из самых нужных, имеющихся в Excel, функций. Она контролирует итог переданного ей логического выражения и возвращает результаты в зависимости от того действительно он либо ложно.
Синтаксис:
=В случае, если(Логическое_выражение;[Значение_если_истина];[Значение_если_ложь])
Примеры применения функции:
Разглядим первый несложный пример, чтобы выяснить, как функция трудится.
Умышлено в первоначальный довод функции засунуть функцию ИСТИНА. В следствии проверки, будет возвращен 2 довод (значение_если_истина), 3 довод будет опущен.
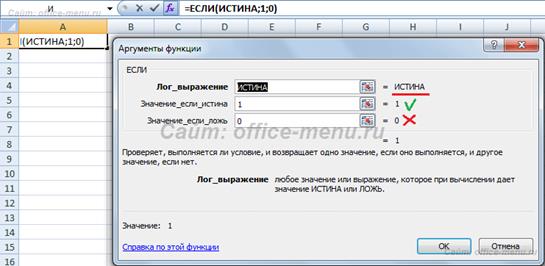
Сейчас приведем пример применения вложенности одной функции В случае, если в другую. Таковой подход может пригодиться, в то время, когда при исполнении (либо невыполнении) одного условия требуется дополнительная проверка.
Условия примера:
Имеются банковские карточки с номерами, начинающимися с первых четырех цифр, каковые являются идентификатором вида карты:
- 1111 – Visa;
- 2222 – Master Card.
Используем отечественную функцию для определения типа карты.
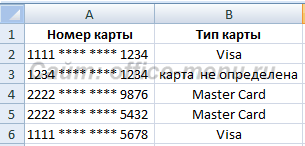
Функция, используемая в данном примере, выглядит так:
=В случае, если(ЛЕВСИМВ(A2;4)=1111; Visa;В случае, если(ЛЕВСИМВ(A2;4)=2222;Master Card;карта не выяснена))
Кроме самой разглядываем функции, в примере употребляется текстовая функция ЛЕВСИМВ, которая возвращает часть текста из строчка, начиная с левого края, числом знаков, заданном вторым ее доводом. С ее помощью мы контролируем, являются ли они равными строке «1111», в случае, если да, возвращаем итог «Visa», в случае, если нет, то делаем положенную функцию В случае, если.
Подобным образом возможно достигнуть большой вложенности и организовывать сложные испытания.
Функция ЕСЛИОШИБКА
Предназначена для проверки возврата выражением неточности. В случае, если неточность найдена, то она возвращает значение второго довода, в противном случае первого.
Функция принимает 2 довода, все они являются необходимыми.
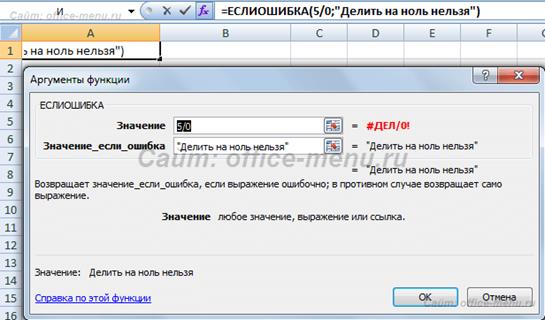
Синтаксис: =ЕСЛИОШИБКА(значение;значение_если_ошибка)
Пример применения функции:
В приведенном примере видно, что выражение в первом доводе возвращает неточность деления на ноль, но так как оно положено в отечественную функцию, то неточность перехватывается и подменяется вторым доводов, то есть строчком «Дробить на ноль запрещено», которую мы ввели самостоятельно. Вместо данной строчка имели возможность бы быть другие функции, все зависит от поставленной перед Вами задачи.
Статистические функции
Использование статистических функций облегчает пользователю статистический анализ данных. Количество дешёвых статистических функций в седьмой версии программы увеличилось, и возможно утверждать, что по спектру дешёвых функций Excel сейчас практически не уступает особым программам обработки статистических данных. Чтобы иметь возможность применять все статистические функции, направляться загрузить надстройку Пакет анализа.
Базу статистического анализа образовывает изучение выборок и совокупностей. Выборка является подмножеством совокупности. Как пример выборки возможно привести опросы публичного мнения. Исследуя выборки посредством отслеживания взаимосвязей и вычисления отклонений с главной совокупностью, возможно проследить, как репрезентативна выборка.
Множество статистических функций Excel рекомендован для анализа возможностей.
Ниже приведено описание некоторых самый распространенных функций. Данные о вторых функциях пользователь может отыскать в справочной системе.
FРАСП
Синтаксис:
FРАСП(х,степени_свободы1,степени_свободы2)
Итог: F-распределение возможности. Эту функцию возможно применять, дабы выяснить, имеют ли два множества данных разные степени плотности. К примеру, возможно изучить результаты женщин и тестирования мужчин, окончивших высшую школу, и выяснить, зависит ли разброс результатов от пола.
Доводы:
- х — значение, для которого вычисляется функция;
- степени_свободы1 — числитель степеней свободы;
- степени_свободы2 — знаменатель степеней свободы.
Возможность
Синтаксис:
Возможность(х_интервал, интервал_вероятностей, нижний_предел, верхний_предел)
Итог: Значение возможности того, что значение из промежутка находится в заданных пределов. Вели довод верхний_предел не задан, то возвращается значение возможности того, что значения в доводе х_интервал равны значению довода нижний_предел.
Доводы:
- х_интервал- промежуток числовых значений х;
- интервал_вероятностей- множество возможностей происхождения значений, входящих в довод х_интервал;
- нижний_предел- нижняя граница значения, для которого вычисляется возможность;
- верхний_предел- необязательная верхняя граница значения, для которого требуется вычислить возможность.
ДИСП
Синтаксис:
ДИСП(число1, число2, …)
Итог: Дисперсия выборки. Доводы рассматриваются как выборка из главной совокупности.
Доводы:
- число1,число2,… — не более 30 доводов; текстовые, логические и безлюдные поля приводят к неточности.
ДИСПР
Синтаксис:
ДИСПР(число1,число2, …)
Итог: Дисперсия главной совокупности. Доводы воображают всю главную совокупность.
Доводы:
- число1,число2,… — не более 30 доводов; текстовые, логические и безлюдные поля приводят к неточности.
ДИСПА
Синтаксис:
ДИСПА(значение1, значение2, …)
Итог: Дисперсия выборки. Доводы рассматриваются как выборка из главной совокупности, содержащей наровне с числовыми и логические значения, и текст.
Доводы:
См. описание функции СТАНДОТКЛОНА.
ПРИМЕЧАНИЕ
Вычисления производятся по той же формуле, что и в функции ДИСП, но учитываются ячейки с текстовыми и логическими значениями.
ДИСПРА
Синтаксис:
ДИСПРА(значение1,значение2,…)
Итог: Дисперсия главной совокупности. Доводы воображают всю главную совокупность.
Доводы:
См. описание функции СТАНДОТКЛОНА.
ПРИМЕЧАНИЕ
Вычисления производятся по той же формуле, что и в функции ДИСПР, но учитываются ячейки с текстовыми и логическими значениями.
ДОВЕРИТ
Синтаксис:
ДОВЕРИТ(альфа, станд_откл, размер)
Итог: Доверительный промежуток для среднего главной совокупности. Доверительный промежуток — окрестность среднего выборки (промежуток, содержащий значение среднего выборки, равноудаленное от финишей промежутка). К примеру, заказав товар по почте, вы имеете возможность выяснить с конкретным уровнем надежности самую раннюю и самую позднюю даты его прибытия.
Доводы:
- альфа — уровень значимости, применяемый для вычисления уровня надежности (уровень надежности равен 100*(1 — альфа)%\ иначе говоря значение альфа, равное 0,05, свидетельствует уровень надежности, равный 95%);
- станд_откл — стандартное отклонение главной совокупности для промежутка данных (предполагается известным);
- размер — размер выборки.
КВАДРОТКЛ
Синтаксис:
КВАДРОТКЛ(число1, число2, …)
Итог: Сумма квадратов отклонений точек данных от их среднего.
Доводы:
- число1, число2, … — от 1 до 30 доводов, для которых вычисляется сумма квадратов отклонений; в функции КВАДРОТКЛ вместо доводов возможно применять массив либо ссылку на массив.
КВПИРСОН
Синтаксис:
КВПИРСОН(известные_значения_у,известные_значения_х)
Итог: Квадрат коэффициента корреляции Пирсона для точек данных в доводах известные_значения_у и известные_значения_х. Значение r-квадрат возможно трактовать как отношение дисперсии для у к дисперсии для х.
Доводы:
- известные_значения_у — массив либо промежуток точек данных;
- известные_значения_х — массив либо промежуток точек данных.
КОВАР
Синтаксис:
КОВАР(массив1, массив2)
Итог: Ковариация (среднее произведений отклонений для каждой пары точек данных). Ковариация употребляется для определения связи между двумя множествами данных. К примеру, возможно проверить, соответствует ли более большому уровню доходов более большой уровень образования.
Доводы:
- массив1 — первый массив либо промежуток данных;
- массив2 — второй массив либо промежуток данных.
КОРЕЛ
Синтаксис:
КОРЕЛ(массив1, массив2)
Итог: Коэффициент корреляции между промежутками ячеек доводов массив1 и массив2. Коэффициент корреляции употребляется для определения наличия связи между двумя особенностями. К примеру, возможно установить зависимость между средней температурой в помещении и наличием кондиционера.
Доводы:
- массив1 — первый массив промежутка данных;
- массив2 — второй массив промежутка данных.
ЛГРФПРИБЛ
Синтаксис:
ЛГРФПРИБЛ(известные_значения_у, известные_значения_х, конст, статистика)
Итог: Возвращает матрицу, обрисовывающую экспоненциальную кривую (у = bm/\х), которая была вычислена из заданных значений: первое значение результирующей матрицы имеется основание экспоненты (т), второе значение — коэффициент (Ь).
Доводы:
- известные_значения_у — множество значений у (в случае, если массив известные_значения_у имеет один столбец, то любой столбец массива известные_значения_х интерпретируется как отдельная переменная; в случае, если массив извест-ные_значения_у имеет одну строчок, то любая строчок массива известные_значения_х интерпретируется как отдельная переменная);
- известные_значения_х — необязательное множество значений х, каковые уже известны для соотношения у = mх + b (массив известиые_знанения_х может содержать одно либо пара множеств переменных; в случае, если употребляется лишь одна переменная, то доводы известные_значения_у известные_значения_х смогут быть массивами любой формы при условии, что они имеют однообразную размерность; в случае, если употребляется более одной переменной, то довод извест-ные_значения_у должен быть вектором (другими словами промежутком высотой в одну строчок либо шириной в один столбец); в случае, если довод известные_значения_х опущен, то предполагается, что это массив {1;2;3;…} для того чтобы же размера, как и массив известные_значе-ния_у);
- конст — логическое значение; в случае, если довод отсутствует либо имеет значение ИСТИНА, то b вычисляется простым методом; в случае, если довод имеет значение Неправда, то Ь надеется равным 1 и знамения т подбираются так, дабы выполнялось соотношение у = m/\х;
- статистика — логическое значение, которое показывает, требуется ли возвращать дополнительную статистику по регрессии (в случае, если довод имеет значение ИСТИНА, то функция ЛГРФПРИБЛ возвращает дополнительную регрессионную статистику, так что возвращаемый массив будет иметь вид: {mn;mn-1;…;m1;b:sen;sen-1;…;se1; seb:r2;sey:F;df:ssreg;ssresid}; в случае, если довод имеет значение Неправда либо опущен, то функция ЛГРФПРИБЛ возвращает лишь коэффициенты т и постоянную Ь).
ЛИНЕЙН
Синтаксис:
ЛИНЕЙН(известные_значения_у,известные_значения_х,конст, статистика)
Итог: Эта функция применяет способ мельчайших квадратов, дабы отыскать уравнение прямой линии, которая наилучшим образом аппроксимирует имеющиеся эти. Функция возвращает массив, что обрисовывает взятую прямую. Уравнение прямой линии имеет следующий вид:
у = m1*1+m2*2+…+b либо у=mх+b
где зависимое значение у есть функцией свободного значения х, т — матрица значений углового коэффициента результирующей прямой, а Ь — абсцисса точки пересечения прямой с Y-осью. Довод ЛИНЕЙН может кроме этого возвращать дополнительную регрессионную статистику.
Доводы:
См. функцию ЛГРФПИБЛ.
ЛОГНОРМОБР
Синтаксис:
ЛОГНОРМОБР(возможность, среднее, стандартное_отклонение)
Итог: Обратная функция логарифмического обычного распределения х, где 1/\(х) имеет обычное распределение с параметрами среднее и стандартное_отклотние. В случае, если р = ЛОГНОРМОБР(х,…), то ЛОГНОРМОБР(p,…)= х, Логарифмическое обычное распределение употребляется для анализа логарифмически преобразованных данных.
Доводы:
- возможность — возможность, которая связана с обычным логарифмическим распределением;
- среднее — среднее ln(x);
- стандартное_отклонение — стандартное отклонение ln(х).
МАКС
Синтаксис:
МАКС(число1, число2, …)
Итог: Громаднейшее значение в перечне доводов.
Доводы:
- число1, число2, … — от 1 до 30 чисел, среди которых ищется большое значение. Возможно задавать доводы, каковые являют -ся числами, безлюдными ячейками, логическими значениями либо текстовыми представлениями чисел; доводы, каковые являются значениями неточности либо текстами, не преобразуемыми в числа, приводят к появлению значений неточности. В случае, если довод есть массивом либо ссылкой, то в нем учитываются лишь числа. Безлюдные ячейки, логические значения, тексты либо значения неточностей в массиве либо ссылке игнорируются. В случае, если доводы не содержат чисел, то функция МАКС возвращает 0.
МЕДИАНА
Синтаксис:
МEДИАНА(число1, число2, …)
Итог: Медиана заданного множества чисел (число, которое есть серединой множества чисел: добрая половина чисел больше, чем медиана, а добрая половина чисел меньше, чем медиана).
Доводы:
- число1, число2, …- числа либо имена, массивы либо адресные ссылки на диапазон ячеек, содержащий ссылки.
МИН
Синтаксис:
МИН(число1, число2, …)
Итог: Мельчайшее значение в перечне доводов.
Доводы:
- число1, число2, … — не более 30 доводов; игнорируются лишь значения неточности и текст, что не может быть преобразован в числа; в случае, если ни один довод не содержит чисел, функция МИН возвращает 0.
МОДА
Синтаксис:
МОДА(число1, число2, …)
Итог: Чаще всего видящееся значение в массиве либо промежутке данных. Равно как и функция МЕДИАНА, функция МОДА есть мерой обоюдного размещения значений.
Доводы:
- число1, число2, … — от 1 до 30 доводов, для которых вычисляется функция МОДА; в функции МОДА возможно применять вместо доводов массив либо ссылку на массив.
НОРМАЛИЗАЦИЯ
Синтаксис:
НОРМАЛИЗАЦИЯ(х, среднее, стандартное_откл)
Итог: Нормализованное значение для распределения, характеризуемого стандартным отклонением и средним.
Доводы:
- х — нормализуемое значение;
- среднее — среднее арифметическое распределения;
- стандартное_откл стандартное отклонение распределения.
ПРИМЕЧАНИЕ
Доводы должны быть числами либо именами, массивами либо ссылками, содержащими числа. Микрософт Excel контролирует все числа, содержащиеся в доводах, каковые являются массивами либо ссылками. В случае, если довод, что есть ссылкой, содержит безлюдные ячейки, текстовые либо логические значения, то такие значения игнорируются; но ячейки, каковые содержат нулевые значения, учитываются.
НОРМРАСП
Синтаксис:
НОРМРАСП(х, среднее, стандартное_откл, интегральная)
Итог: Обычная функция распределения для стандартного отклонения и указанного среднего. Эта функция имеет весьма широкий диапазон применения в статистике, включая диагностику догадок.
Доводы:
- х — значение, для которого строится распределение;
- среднее — среднее арифметическое распределения;
- стандартное_откл — стандартное отклонение распределения;
- интегральная — логическое значение, определяющее форму функции (в случае, если довод интегральная имеет значение ИСТИНА, то функция НОРМРАСП возвращает интегральную функцию распределения; в случае, если данный довод имеет значение Неправда, то возвращается функция плотности распределения).
ПРЕДСКАЗ
Синтаксис:
ПРЕДСКАЗ(х, известные_значения_у, известные_значения_х)
Итог: Значение функции в точке х, предсказанное на базе линейной регрессии, для массивов известных значений х и у либо промежутков данных. Эту функцию возможно применять для прогнозирования будущих продаж, потребностей в оборудовании либо тенденций потребления.
Доводы:
- х — точка данных, для которой прогнозируется значение;
- известные_значения_у — зависимый массив либо промежуток данных;
- известные_значения_х — свободный массив либо промежуток данных.
РАНГ
Синтаксис:
РАНГ(число, ссылка, порядок)
Итог: Ранг числа в перечне чисел. Ранг числа — это показатель его величины довольно вторых значений в перечне. (В случае, если перечень упорядочить, то ранг числа будет его позицией.)
Доводы:
- число — число, для которого определяется ранг;
- ссылка — массив либо ссылка на перечень чисел (нечисловые значения в ссылке игнорируются);
- порядок — число, определяющее метод упорядочения (в случае, если порядок равен 0 либо опущен, то Excel определяет ранг числа так, как если бы ссылка была перечнем, упорядоченным в порядке убывания; в случае, если порядок — это любое ненулевое число, то Excel определяет ранг числа так, как если бы ссылка была перечнем, упорядоченным в порядке возрастания).
ПРИМЕЧАНИЕ
Однообразные числа приобретают однообразный ранг в перечне.
РОСТ
Синтаксис:
РОСТ(известные_значения_у, известные_значения_х, новые_значения_х, конст)
Итог: Аппроксимирует экспериментальной кривой известные_значения_у и извест-ные_значения_х и возвращает значения данной кривой, соответствующие значениям х, каковые определяются доводом новые_значения_х.
Доводы:
- известные_значения_у — множество значений у, каковые уже изиестны для соотношения у — b*m/\х (в случае, если массив известные_значения_у имеет один столбец, то любой столбец массива известные_значения_х интерпретируется как отдельная переменная; в случае, если массив известные^ значения_у имеет одну строчок, то любая строчок массива известные_значения_х интерпретируется как отдельная переменная; в случае, если какие-либо числа в массиве известные_значения_у равны 0 либо отрицательны, то функция РОСТ возвращает значение неточности #ЧИСЛО!);
- известные_значения_х — необязательное множество значений х, каковые уже известны для соотношения у = b *m/\х (массив известные_значения_х может содержать одно либо пара множеств переменных; в случае, если употребляется лишь одна переменная, то извест-ные_значения_у и известные_значения_х смогут иметь любую форму при условии, что они имеют однообразную размерность; в случае, если употребляется более одной переменной, то узнаваемые:_значения_у должны быть вектором (другими словами промежутком высотой в одну строчок либо шириной в один столбец); в случае, если довод известные_значения_х опущен, то предполагается, что это массив {1;2;3;…} для того чтобы же размера, как и известные_значения_у);
- новые_значения_х — новые значения х, для которых функция РОСТ возвращает соответствующие значения у (довод новые_значения_х обязан содержать столбец (либо строчок) для каждой свободной переменной, как и известные_значения_х\ так, в случае, если довод известные_значения_у — это один столбец, то доводы известные_значения_х и но-вые_значения_х должны иметь такое же количество столбцов; в случае, если довод известные_значения_у — это одна строчок, то доводы известные_зна-чения_х и новые__значения_х должны иметь такое же количество строчков; в случае, если довод новые_значения_х опущен, то предполагается, что он сходится с доводом известные_значения_х в случае, если оба довода известные_значения_х и новые_ значе-ния_х опущены, то предполагается, что это массив {1;2;3;…} для того чтобы же размера, как и извест-ныезначения_у);
- конст — логическое значение; в случае, если довод конст отсутствует либо имеет значение ИСТИНА, то b вычисляется традиционно; в случае, если довод конст имеет значение Неправда, то Ъ надеется равным 1 и значения т подбираются так, дабы выполнялось соотношение у=m/\х.
СРГЕОМ
Синтаксис:
СРГЕОМ(число1, число2, …)
Итог: Среднее геометрическое значений массива либо промежутка положительных чисел. К примеру, функцию СРГЕОМ возможно применять для вычисления средних темпов роста, в случае, если задан составной доход с переменными ставками.
Доводы:
- число1, число2, … — от 1 до 30 доводов, для которых вычисляется среднее геометрическое; в функции СРГЕОМ вместо доводов возможно применять массив либо ссылку на массив.
СРЗНАЧ
Синтаксис:
СРЗНАЧ(число1, число2, …)
Итог: Среднее значение (среднее арифметическое) доводов.
Доводы:
- число1, число2, … — числа либо имена, массивы либо адресные ссылки на диапазон ячеек, содержащий ссылки. Функция СРЗНАЧ разрешает задавать от 1 до 30 доводов.
СРОТКЛ
Синтаксис:
СРОТКЛ(число1, число2, …)
Итог: Среднее полных значений отклонений точек данных от среднего. Функция СРОТКЛ есть мерой разброса множества данных.
Доводы:
- число1, число2, … — от 1 до 30 доводов, для которых определяется среднее безотносительных отклонений; вместо доводов в функции СРОТКЛ возможно применять массив либо ссылку на массив.
СТАНДОТКЛОН
Синтаксис:
СТАНДОТКЛОН(число1, число2, …)
Итог: Оценка стандартного отклонения по выборке. Стандартное отклонение — это мера того, как обширно разбросаны точки данных довольно их среднего.
Доводы:
- число1, число2, … — от 1 до 30 числовых доводов, соответствующих выборке из главной совокупности.
ПРИМЕЧАНИЕ
Применяйте эту функцию, дабы вычислить стандартное отклонение главной совокупности на основании выборки.
СТАНДОТКЛОНП
Синтаксис:
СТАНДОТКЛОНП(число1,число2,…)
Итог: Стандартное отклонение по главной совокупности. Стандартное отклонение — это мера того, как обширно разбросаны точки данных довольно их среднего.
Доводы:
- число1, число2, …- от 1 до 30 числовых доводов, соответствующих главной совокупности; возможно применять массив либо ссылку на массив вместо доводов, разделяемых точкой с запятой.
ПРИМЕЧАНИЕ
Применяйте эту функцию, дабы вычислить стандартное отклонение главной совокупности на базе всех данных.
СТАНДОТКЛОНА
Синтаксис:
СТАНДОТКЛОНА(значение1, значение2, …)
Итог: Оценка стандартного отклонения по выборке, содержащей наровне с числовыми и логические значения, и текст.
Доводы:
- значение1, значение2, … — От 1 до 30 доводов, соответствующих выборке из главной совокупности. Возможно применять массив либо ссылку на массив вместо перечисляемых через запятую доводов. Для вычисления стандартного отклонения используется та же формула, которая употребляется в функции СТАНДОТКЛ. Но значения доводов смогут быть не только числовыми, но и текстовыми, и логическими значениями. Довод, содержащий значение ИСТИНА, при вычислении заменяется на 1, а довод, включающий значение Неправда либо текст, — на 0.
СТАНДОТКЛОНПА
Синтаксис:
СТАНДОТКЛОНПА(значение1, значение2, …)
Итог: Оценка стандартного отклонения по главной совокупности, содержащей наровне с числовыми и логические значения, и текст.
Доводы:
См. описание функции СТАНДОТКЛОНА.
ПРИМЕЧАНИЕ
Для выборок громадного количества СТАНДОТКЛОНПА и СТАНДОТКЛОНА дают родные результаты. Функция СТАНДОТКЛОНА возвращает несмещенную оценку стандартного отклонения, а функция СТАНДОТКЛОНПА — смещенную оценку.
СЧЕТ
Синтаксис:
СЧЕТ(значение1, значение2, …)
Итог: Количество чисел в перечне доводов. Функция СЧЕТ употребляется чтобы получить количество числовых ячеек в промежутках либо массивах ячеек.
Доводы:
- значение1, значение2, … — не более 30 доводов; в случае, если аргуменг есть матрицей либо адресной ссылкой, то в нем при подсчете учитываются лишь числа, в остальных случаях учитываются безлюдные поля, числовые поля, текстовые представления и логические значения чисел (но не значения неточности либо не преобразуемы и текст).
СЧЕТЗ
Синтаксис:
СЧЕТЗ(значение1, значение2, … )
Итог: Количество всех значений (любого типа), приведенных в качестве доводов.
Доводы:
- значение1, значение2, … — не более 30 доводов; в матрицах и адресуемых диапазонах безлюдные поля игнорируются.
ЧАСТОТА
Синтаксис:
ЧАСТОТА(массив_данных, массив_карманов)
Итог: Распределение частот в виде вертикального массива. Для данного множества значений и данного множества карманов (карман соответствует понятию промежутка в математике) частотное распределение показывает, сколько исходных значений попадает в любой промежуток.
Доводы:
- массив_данных — массив либо ссылка на множество данных, для которых вычисляются частоты; в случае, если довод массив_данных не содержит значений, то функция ЧАСТОТА возвращает массив нулей;
- массив_карманов — массив либо ссылка на множество промежутков, в каковые группируются значения довода массив_дан-ных\ в случае, если довод массив_карманов не содержит значений, то функция ЧАСТОТА возвращает количество элементов в доводе массив_данных.
ПРИМЕЧАНИЕ
Функция ЧАСТОТА не учитывает ни текст, ни безлюдные ячейки.
ЭКСПРАСП
Синтаксис:
ЭКСПРАСП(х, лямбда, интегральная)
Итог: Экспоненциальное распределение. Функция ЭКСПРАСП употребляется для моделирования временных задержек между событиями, к примеру для определения того, сколько времени займет финансовый перевод в автоматизированном банке. Посредством функции ЭКСПРАСП возможно подсчитать возможность того, что данный процесс займет, предположим, не более 60 секунд.
Доводы:
- х — значение функции;
- лямбда — значение параметра;
- интегральная — логическое значение, которое показывает, какую форму экспоненциальной функции применять (в случае, если довод интегральная имеет значение ИСТИНА, то функция ЭКСПРАСП возвращает интегральную функцию распределения; в случае, если данный довод имеет значение Неправда, то возвращается функция плотности распределения).
Математические функции
В данной статье будет рассмотрена та часть математических функций, которая чаще всего используется в ответе разных задач. С полным списком возможно ознакомиться на вкладке «Формулы» = выпадающий перечень «Математические»:
Какие конкретно функции затронет статья: