Тригонометрические функции.
неравенства и Тригонометрические уравнения.
Свойства и графики тригонометрических функций.
Определение: Тригонометрической функцией числового довода х именуется тригонометрическая функция угла, содержащего х радиан.
, , , .
Свойства и график тригонометрической функции .
| x |
| y |
| у = 1 |
| у = — 1 |
| y |
1. Область определения функции: .
2. Множество значений функции:
Вывод: График функции расположен между прямыми y = -1 ; y = 1 .
3. Функция нечетная, другими словами .
Вывод: График функции симметричен относительно начала координат.
4. Функция периодическая, поскольку .
Вывод:График функции повторяется через 2p.
5. Функция не монотонная:
возрастает от-1до 1 ;
убывает от 1 до-1 .
6. Функция необратимая на области определения.
7. y = 0; sin x = 0 при x = pk -нули функции.
8. Функция ограниченная, поскольку .
при
при
| x |
| y |
| -1 |
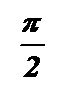
|
| p |
| 2p |
| — p |
| — 2p |
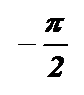
|
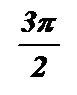
|
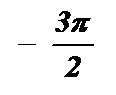
|
График функции именуется синусоидой.
| x |
| y |
| у = 1 |
| у = — 1 |
Свойства и график тригонометрической функции .
1. Область определения функции: ) .
2. Множество значений функции: .
Вывод: График функции расположен между прямыми y = -1 ; y = 1 .
3. Функция четная, другими словами
Вывод: График функции симметричен относительно оси ординат.
4. Функция периодическая, поскольку .
Вывод:График функции повторяется через 2p.
5. Функция не монотонная:
убывает от 1 до- 1;
возрастает от- 1 до 1 .
6. Функция необратимая на области определения.
7. y = 0; при .
8. Функция ограниченная, поскольку .
при ,
| x |
| y |
| -1 |
| p |
| 2p |
| — p |
| -2p |
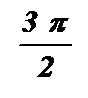
|
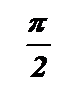
|
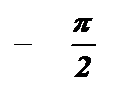
|
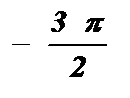
|
при
График функции именуется косинусоидой.
Свойства и график тригонометрической функции .
1. Область определения функции: либо .
2. Множество значений функции: .
Вывод: График функции расположен между прямыми , .
3. Функция нечетная, другими словами .
Вывод: График функции симметричен относительно начала координат.
4. Функция периодическая, поскольку как tg ( x + pk ) = tg x , k IZ.
Вывод:График функции повторяется через p.
5. Функция не монотонная на всей области определения, но функция возрастающая в каждом из промежутков .
6. Функция необратимая на области определения.
7. ; при -нули функции.
8. Функция неограниченная, поскольку .
График функции именуется тангенсоидой.
| y |
| x |
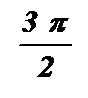
|
| p |
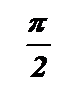
|
| -1 |
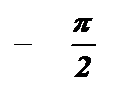
|
| — p |
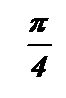
|
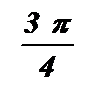
|
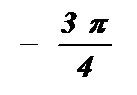
|
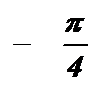
|
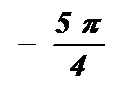
|
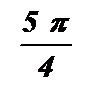
|
Свойства и график тригонометрической функции .
1. Область определения функции: либо .
2. Множество значений функции: .
Вывод: График функции расположен между прямыми , .
3. Функция нечетная, другими словами .
Вывод: График функции симметричен относительно начала координат.
4. Функция периодическая, поскольку сtg ( x + pk ) = сtg x , k IZ.
Вывод:График функции повторяется через p.
5. Функция не монотонная на всей области определения, но функция убывающая в каждом из промежутков xI( 0+pk ; p+pk ) , k IZ.
6. Функция необратимая на области определения.
7. y = 0; при -нули функции.
8. Функция неограниченная, поскольку .
График функции именуется котангенсоидой.
| x |
| y |
|
| p |
|
| -1 |
|
| — p |
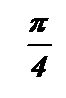
|
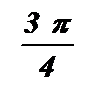
|
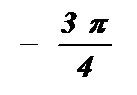
|
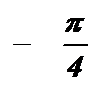
|
|
| 2 p |
|
Тригонометрические уравнения.
Несложные тригонометрические уравнения.
Определение: Уравнение именуется тригонометрическим, если оно содержит переменную лишь под символами тригонометрических функций.
Определение: Решить тригонометрическое уравнение – значит отыскать все настоящие числа, обращающие уравнение в тождество, либо доказать что их нет.
Пример: Решить уравнение: cos х – sin х = 0.
Ответ: Данное уравнение равносильно уравнению cos х = sin х .
Углы, радианные меры которых удовлетворяют этому уравнению, смогут пребывать в первой и третьей координатных четвертях, поскольку косинус и синус имеют в них однообразные символы. косинус и Синус имеют однообразные значения при углах х = 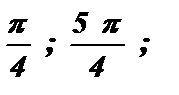 … либо х =
… либо х = 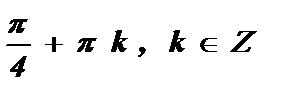 .
.
Ответ: х = 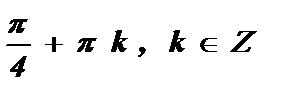 .
.
Определение: Несложные тригонометрические уравнения — это уравнения вида: sin х = а , cos х = а , tg х = а , ctg х = а , где
а – данное настоящее число.
Замечание: Ответ любого тригонометрического уравнения сводится к ответу несложных тригонометрических уравнений .
Так как тригонометрические функции являются периодическими функциями, достаточно отыскать корни уравнений на отрезке длиной равной главному периоду тригонометрической функции.
sin х = а
1. а 1 , а – 1 , sin х = а корней нет.
2. а = 1 , не сильный х = 1 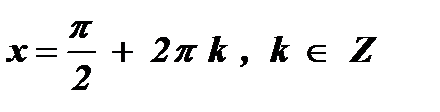 .
.
3. а = 0 , sin х = 0 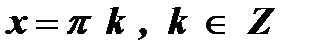 .
.
4. а = – 1 , sin х = – 1 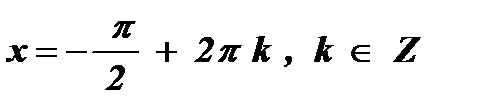 .
.
5. – 1 а 1 , sin х = а х 1 = arcsin а + 2pk , k I Z
х 2 = p – arcsin а + 2pk , k I Z .
Либо
х 1,2 = ( – 1 ) к · arcsin а + pk , k I Z .
Пример: Решить уравнения:
№1. sin 3х = – 1 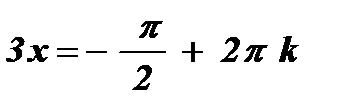
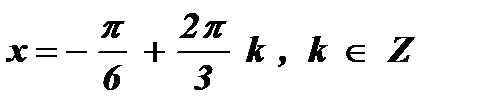 .
.
№2. sin ( 2х – 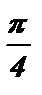 ) = 0 2х –
) = 0 2х – 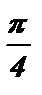 = pk 2х =
= pk 2х = 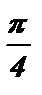 + pk
+ pk 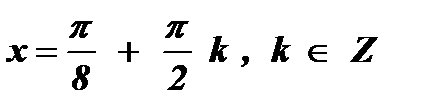
№3. sin 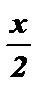 =
= 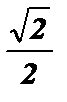
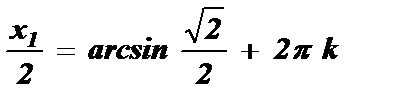
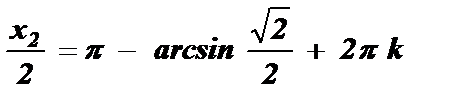
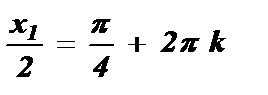
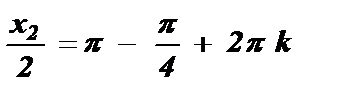
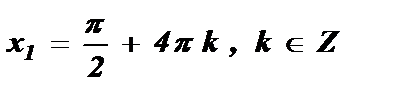
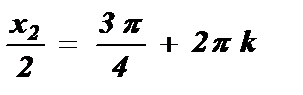
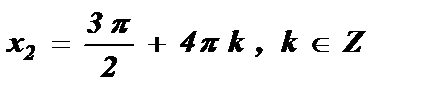
Ответ: 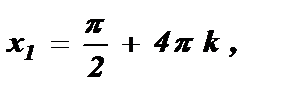
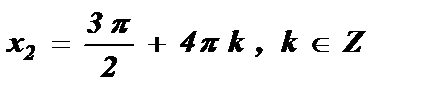 .
.
cos х = а
1. а 1 , а – 1 , cos х = а корней нет .
2. а = 1 , cos х = 1 х = 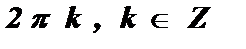 .
.
3. а = 0 , cos х = 0 х = 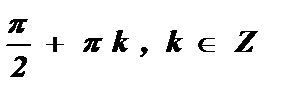 .
.
4. а = – 1 , cos х = – 1 х = 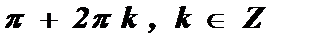 .
.
5. – 1 а 1 , cos х = а х 1 = arccos а + 2pk , k I Z
х 2 = – arccos а + 2pk , k I Z .
Либо
х 1,2 = ± arccos а + 2pk , k I Z .
Пример: Решить уравнения:
№1. cos ( 3х – 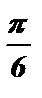 ) = 1 3х –
) = 1 3х – 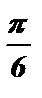 = 2pk 3х =
= 2pk 3х = 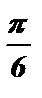 + 2pk х =
+ 2pk х = 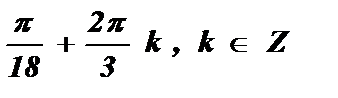 .
.
№2. cos ( х – 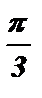 ) =
) = 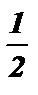 х1 –
х1 – 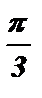 = arccos
= arccos 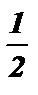 + 2pk х2 –
+ 2pk х2 – 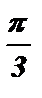 = – arccos
= – arccos 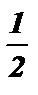 + 2pk
+ 2pk
х1 – 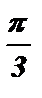 =
= 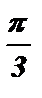 + 2pk х2 –
+ 2pk х2 – 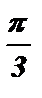 = –
= – 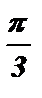 + 2pk
+ 2pk
х1 = 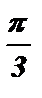 +
+ 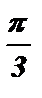 + 2pk х2 = –
+ 2pk х2 = – 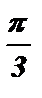 +
+ 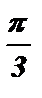 + 2pk
+ 2pk
х1 = 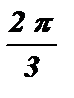 + 2pk , k I Z . х2 = 2pk , k I Z .
+ 2pk , k I Z . х2 = 2pk , k I Z .
Ответ: х1 = 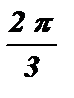 + 2pk , х2 = 2pk , k I Z .
+ 2pk , х2 = 2pk , k I Z .
№3. cos 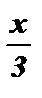 =
= 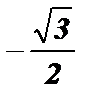
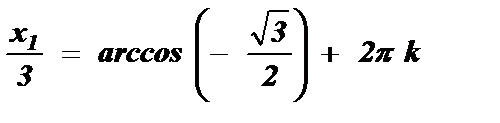
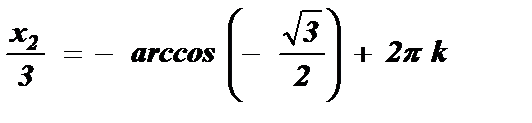
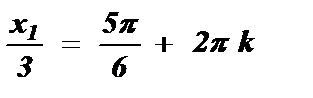
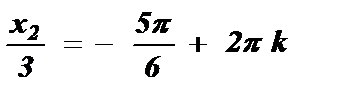
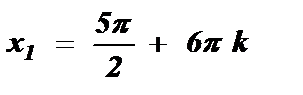 , k I Z
, k I Z 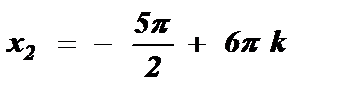 , k I Z .
, k I Z .
Ответ: 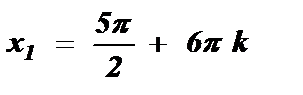 ,
, 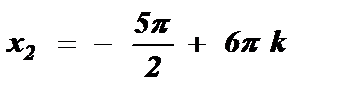 , k I Z .
, k I Z .
tg х = а , а — любое число, х = arctg а + pk , k I Z
ctg х = а , а — любое число, х = arcсtg а + pk , k I Z
Пример:
№1. tg 2х = 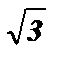 2х = arctg
2х = arctg 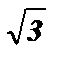 + pk 2х =
+ pk 2х = 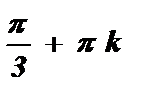
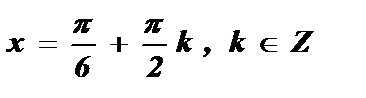 .
.
№2. сtg 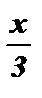 = 7
= 7 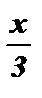 = arcсtg 7 + pk x = 3 arcсtg 7 + 3 pk , k I Z .
= arcсtg 7 + pk x = 3 arcсtg 7 + 3 pk , k I Z .
№3. сtg 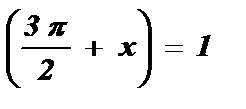 tg x = — 1 x = arctg (- 1 ) + pk x =
tg x = — 1 x = arctg (- 1 ) + pk x = 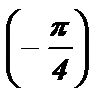 + pk , k I Z .
+ pk , k I Z .
20. 2. Тригонометрические уравнения, приводимые к квадратному.
Замечание: При ответе тригонометрических уравнений целого вида, содержащих косинусы и синусы, область допустимых значений не устанавливается, поскольку эти функции выяснены для любого настоящего значения.
Пример №1: Решить уравнение: 8 sin 2 x — 6 sin x — 5 = 0 .
Ответ:
Введем новую переменную у = sin x , возьмём квадратное уравнение:
8 у 2 — 6 у — 5 = 0; D = b 2 — 4ac; D = (- 6 )2 — 4 · 8 · (- 5 ) = 196;
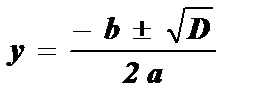 ;
; 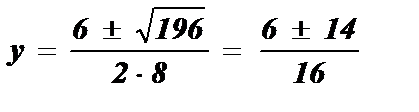 ; y1 =
; y1 = 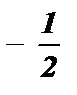 ; y2 =
; y2 = 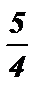 ;
;
sin x = 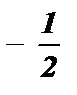 ; х 1,2 = ( – 1 ) к · arcsin
; х 1,2 = ( – 1 ) к · arcsin 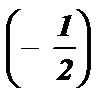 +pk ; х 1,2 = ( – 1 ) к ·
+pk ; х 1,2 = ( – 1 ) к · 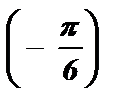 +pk ;
+pk ;
х 1,2 = ( – 1 ) к+1 · 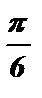 + pk , k I Z ;
+ pk , k I Z ;
sin x = 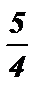 корней нет , так как — 1 ? sin x ? 1 .
корней нет , так как — 1 ? sin x ? 1 .
Ответ: х 1,2 = ( – 1 ) к+1 · 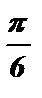 + pk , k I Z .
+ pk , k I Z .
Пример №2: Решить уравнение: 8 sin 2 3x + 6 cos 3x — 3 = 0 .
Ответ:
Применяя формулу cos 2 3x + sin 2 3x = 1 , заменим sin 2 3x = 1 — cos 2 3x .
8 (1 — cos 2 3x ) + 6 cos 3x — 3 = 0; 8 — 8 cos 2 3x + 6 cos 3x — 3 = 0;
— 8 cos 2 3x + 6 cos 3x + 5 = 0; 8 cos 2 3x — 6 cos 3x — 5 = 0;
Введем новую переменную у = cos 3x , возьмём квадратное уравнение:
8 у 2 — 6 у — 5 = 0; D = b 2 — 4ac; D = (- 6 )2 — 4 · 8 · (- 5 ) = 196;
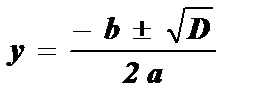 ;
; 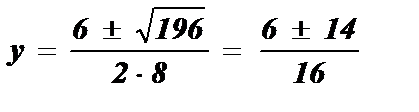 ; y1 =
; y1 = 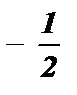 ; y2 =
; y2 = 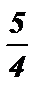 ;
;
cos 3x = 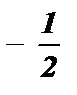 ; 3х = ± arccos
; 3х = ± arccos 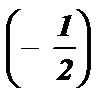 + 2pk ; 3х = ±
+ 2pk ; 3х = ± 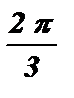 + 2pk ;
+ 2pk ;
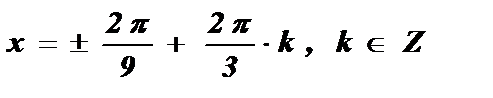 .
.
cos 3x = 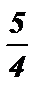 корней нет , так как- 1 ? cos 3x ? 1 .
корней нет , так как- 1 ? cos 3x ? 1 .
Ответ: 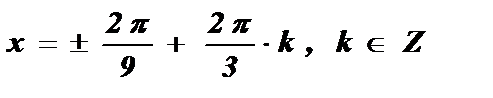 .
.
Пример №3: Решить уравнение: 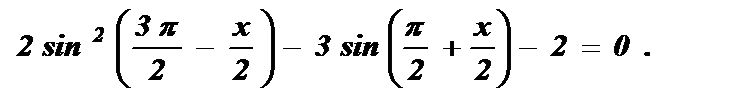
Ответ:
Воспользуемся формулами приведения:
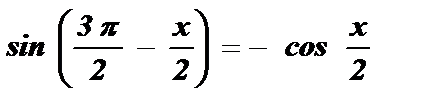 ;
; 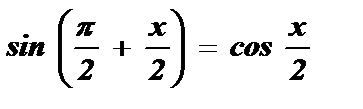 ;
;
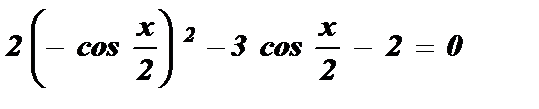 ;
; 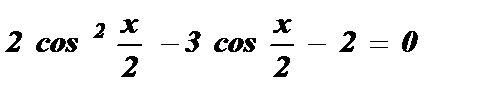 ;
;
Введем новую переменную у = cos 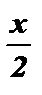 , возьмём квадратное уравнение:
, возьмём квадратное уравнение:
2 y 2 — 3 y — 2 = 0; D = b 2 — 4ac; D = (- 3 )2 — 4 · 2 · (- 2 ) = 25;
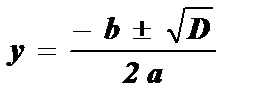 ;
; 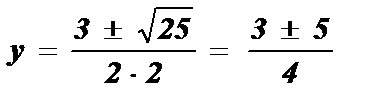 ; y1 =
; y1 = 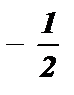 ; y2 = 2;
; y2 = 2;
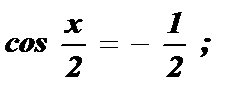
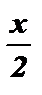 = ± arccos
= ± arccos 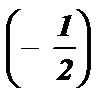 + 2pk ;
+ 2pk ; 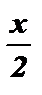 = ±
= ± 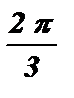 + 2pk ;
+ 2pk ;
x = ± 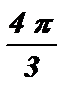 + 4pk , k I Z .
+ 4pk , k I Z .
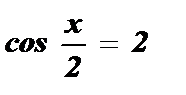 корней нет , так как — 1 ? cos
корней нет , так как — 1 ? cos 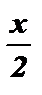 ? 1 .
? 1 .
Ответ: x = ± 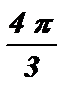 + 4pk , k I Z .
+ 4pk , k I Z .
Пример №4: Решить уравнение: 3 cos 2 x = 7 sin x .
Ответ:
Воспользуемся формулой cos 2x = 1 — 2 sin 2 x :
3 (1 — 2 sin 2 x ) — 7 sin x = 0; 3 — 6 sin 2 x — 7 sin x = 0;
Введем новую переменную у = sin x , возьмём квадратное уравнение:
— 6 y 2 — 7 y + 3 = 0; 6 y 2 + 7 y — 3 = 0; D = b 2 — 4ac; D = 7 2 — 4 · 6 · (- 3 ) = 121;
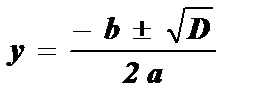 ;
;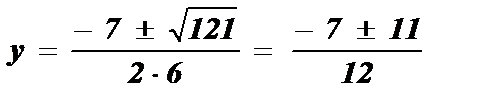 ;y1=
;y1= 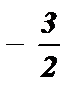 ; y2 =
; y2 = 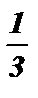 ;
;
sin x = 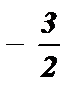 корней нет , так как — 1 ? sin x ? 1 .
корней нет , так как — 1 ? sin x ? 1 .
sin x = 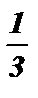 х 1,2 = ( – 1 ) к · arcsin
х 1,2 = ( – 1 ) к · arcsin 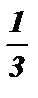 +pk , k I Z .
+pk , k I Z .
Ответ: х 1,2 = ( – 1 ) к · arcsin 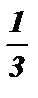 +pk , k I Z .
+pk , k I Z .
20. 3. Однородные тригонометрические уравнения .
Определение: Тригонометрическое уравнение вида a sin x + b cos x = 0
(a I R , b I R , a ¹ 0 , b ¹ 0 ) именуется однородным первой степени довольно sin x иcos x .
Определение: Тригонометрическое уравнение вида a sin 2 x + b sin x cos x + с cos 2x = 0
(a I R , b I R , с I R , a ¹ 0 , b ¹ 0 , с ¹ 0 ) называетсяоднородным второй степени довольно sin x иcos x .
Метод ответа:Значения довода х, при которых sin x = 0 илиcos x = 0,не являются корнямитригонометрического уравнения однородного n-ой
степени довольно sin x иcos x, поскольку в случае, если sin x = 0
(cos x = 0),то из данного уравнения направляться равенство cos x = 0
(sin x = 0), а из главного тригонометрического тождества направляться, что синус и косинус не смогут быть одновременно равными нулю. Исходя из этого дабы решить тригонометрическое уравнение однородное n-ой степени довольно sin x иcos x , возможно обе части уравнения поделить на 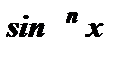 либо
либо 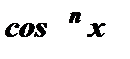 .
.
Пример №1: Решить уравнение:sin x + 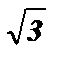 cos x = 0 .
cos x = 0 .
Ответ:
При ответе тригонометрических уравнений, содержащих дроби, устанавливается область допустимых значений, поскольку нужно исключить значения переменной, при которых знаменатели дробей обращаются в нуль.
Пример №1: Решить уравнение: sin x tg x + 1 = sin x + tg x .
Ответ:
| х |
| у |
Определим область допустимых значений данного уравнения: tg x не существует при углах вертикального диаметра , значит х ¹ 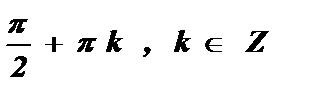 .
.
sin x tg x + 1 — sin x — tg x = 0;
Преобразуем левую часть в произведение посредством группировки:
sin x tg x — sin x + 1 — tg x = 0;
sin x ( tg x — 1 ) — ( tg x — 1 ) = 0;
( tg x — 1 ) ( sin x — 1 ) = 0;
Тригонометрические функции.
неравенства и Тригонометрические уравнения.