Последовательное развитие данной идеи и рвение совершенно верно обрисовать логические средства вывода теорем из теорем привели Гильберта к концепции формального А. м., характерной для третьей, современной его стадии. Главная мысль Гильберта – полная формализация языка науки, при которой её суждения рассматриваются легко как последовательности знаков (формулы), не имеющие как таковые никакого смысла (что они покупают только при некоей конкретной интерпретации). Это относится и к теоремам – как общелогическим, так и своеобразным для данной теории. Для вывода теорем из теорем (и по большому счету одних формул из вторых) формулируются особые правила вывода (к примеру, т. н. правило modus ponens – «правило зачёркивания», разрешающее взять В из А и «А влечёт В»). Подтверждение в таковой теории (исчислении) либо формальной совокупности – это легко последовательность формул, любая из которых или имеется теорема, или получается из прошлых формул последовательности по какому-либо правилу вывода. В отличие от таких формальных доказательств, свойства самой формальной совокупности в целом обсуждаются – а время от времени их удаётся и доказать – содержательными средствами т. н. метатеории, т. е. теории, разглядывающей данную («предметную») теорию как предмет изучения. На языке метатеории (метаязыка) формулируются и правила вывода предметной теории. По плану Гильберта, в рамках созданной им теории доказательств, т.е. допуская в метатеории лишь т. н. финитные методы рассуждения (не применяющие ссылки ни на какие конкретно объекты, не имеющие конечного построения), возможно было бы доказать отсутсвие противоречий и полноту всей хорошей математики (т. е. доказуемость каждой формулы, подлинной при некоей определённой интерпретации). Не обращая внимания на последовательность больших результатов в этом направлении, гильбертовская программа в целом (её в большинстве случаев именуют формализмом) невыполнима, т. к., в соответствии с ответственному результату К. Гёделя (См. Гёдель) (1931), любая достаточно богатая непротиворечивая формальная совокупность обязательно неполна (т. н. теорема о неполноте). Теорема Гёделя говорит об ограниченности А. м. (не смотря на то, что определённые расширения допускаемых метатеоретических средств и разрешили германскому математику Г. Генцену, П. С. Новикову и др. математикам взять подтверждение непротиворечивости формализованной математики).
А. м. подвержен кроме этого критике, исходящей из разных семантических параметров. Так, интуиционисты (Л. Э. Я. Брауэр, Г. Вейль и др.) не признают обоснованности в применении к нескончаемым множествам принципа исключенного третьего, в это же время данный принцип не только берётся в качестве логической теоремы в большинстве формальных теорий, но и употребляется по существу (не смотря на то, что и неявно) в главных предпосылках гильбертовской программы, в соответствии с которой непротиворечивость теории – достаточное условие её «истинности». Как и интуиционизм, конструктивное направление в математике (в СССР – А. А. Марков и Н. А. Шанин) вычисляет назначением математики изучение не произвольных моделей непротиворечивых формальных совокупностей, а только совокупностей объектов, допускающих в определённом смысле действенное построение.
Ещё более значительные возражения против А. м. выдвигает ультраинтуиционистская критика, ставящая под сомнение единственность натурального последовательности чисел и, тем самым, однозначную определённость понятия теоремы формальной совокупности. В соответствии с данной критике, А. м. основан на «принципе локальности для доказательств», предполагающем, что в случае, если теоремы подлинны и правила вывода сохраняют истинность, то подлинными обязательно должны быть и теоремы. Т. о., интуитивное обоснование общеупотребительного принципа математической индукции, в соответствии с ультраинтуиционистской критике, содержит неустранимый порочный круг. Ультраинтуиционизм, не ограничиваясь критикой, предлагает и хорошую программу преодоления указанных трудностей.
Неспециализированные указания.
Поиск информации по разрешённому вопросу осуществлять самостоятельно, применяя соответствующую литературу, другие источники и Интернет.
Объем работы не должен быть менее 10 страниц самостоятельно отысканного материала.
Работа 2. Элементы теории множеств. Операции над множествами.
Цель работы:
Изучение начальных положений теории множеств и практика работ с дискретными множествами.
Ниже приводятся кое-какие положения теории множеств.
Элементы теории множеств
Логические знаки
Квантор – заменяет выражение для любого, для произвольного, для какого именно бы ни было.
Квантор – заменяет выражение существует, найдется.
Запись (импликация) свидетельствует, что из справедливости высказывания A вытекает справедливость высказывания B. В случае, если, помимо этого, из справедливости высказывания B вытекает справедливость A, то записываем . В случае, если , то высказывание B есть нужным и достаточным условием чтобы выполнялось высказывание A.
В случае, если предложения A и B честны в один момент, то записываем . В случае, если же справедливо хотя бы одно из предложений A либо B, то записываем .
Операции над множествами
Математическое понятие множества элементов принимается в качестве интуитивного. Множество задается правилом либо показателем, в соответствии с которому определяем, в собственности ли этот элемент множеству либо не в собственности.
Множество обозначают знаком A = {x}, где x – неспециализированное наименование элементов множества A. Довольно часто множество записывают в виде A = {a, b, c, …}, где в фигурных скобках указаны элементы множества A. Будем пользоваться обозначениями:
N – множество всех натуральных чисел;
Z – множество всех целых чисел;
Q – множество всех рациональных чисел;
R – множество всех настоящих чисел;
C – множество всех комплексных чисел;
Z0 – множество всех неотрицательных целых чисел.
Запись (либо ) свидетельствует, что элемент a в собственности множеству A.
Запись (либо ) свидетельствует, что элемент a не в собственности множеству A.
Множество B, все элементы которого принадлежат множеству A, именуется подмножеством множества A, и наряду с этим записывают (либо ) (см. рисунок 8).
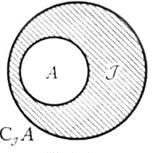
Рисунок 7
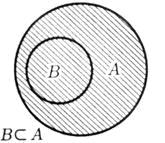
Рисунок 8
В любой момент , так как любой элемент множества, конечно, в собственности A. Безлюдное множество, т. е. множество, не содержащее ни одного элемента, обозначим знаком O. Любое множество содержит безлюдное множество в качестве собственного подмножества.
В случае, если , то A и B именуются равными множествами, наряду с этим записывают A = B.
В случае, если , то множество элементов множества , не принадлежащих A, именуется дополнением множества A к множеству (см. рисунок 7).
Дополнение множества A к множеству обозначают знаком СJА; либо легко CA, в случае, если известно, к какому множеству берется дополнение. Так,
В случае, если , то время от времени дополнение множества B к множеству A именуют разностью множеств A и B и обозначают A\B (см. рисунок 9), т. е.:
Пускай A и B – подмножества множества .
Объединением множеств A и B именуется множество (см. рисунок 10)
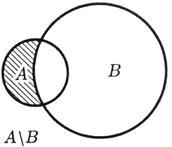
Рисунок 9
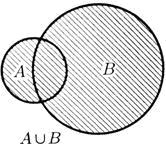
Рисунок 10
Подобно, в случае, если , j = , подмножества множества , то их объединением будет множество:
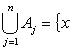
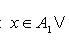
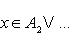
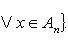
Пересечением подмножеств A и B именуется множество (см. рисунок 11)
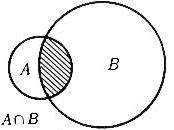
Рисунок 11
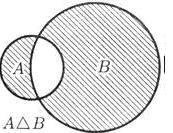
Рисунок 12
Подобно, знаком обозначают пересечение подмножеств , множества , т. е. множество
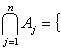
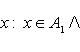
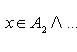
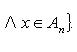
В случае, если каждому сопоставлено некое множество , то говорят, что задано семейство множеств . В этом случае множество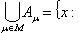 
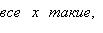
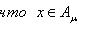
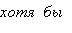
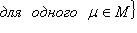именуют объединением семейства множеств , а множество
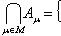
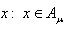
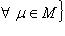
– о пересечением этого семейства.
Симметрической разностью двух множеств A и B именуется множество, определяемое объединением разностей A\B и B\A (см. рисунок 12).
Симметрическую разность обозначают знаком .
Два элемента a и b именуются упорядоченной парой, в случае, если указано, какой из этих элементов первый, какой второй, наряду с этим .
Упорядоченную несколько элементов a и b обозначают знаком (a, b).
Подобно определяется упорядоченная совокупность из n элементов a1, a2, …, an, которую обозначают знаком (a1, a2, …, an). Элементы a1, a2, …, an именуются координатами упорядоченной совокупности (a1, a2, …, an).
Совокупность всевозможных упорядоченных пар (a, b), где , именуется произведением множеств A и B и обозначается знаком .
Подобно, знаком обозначают произведение множеств , т. е. совокупность всевозможных упорядоченных совокупностей (a1, a2, …, an), где .
Пускай A, B и D — произвольные подмножества множества . Тогда из определений объединения, пересечения и дополнения вытекают следующие предложения:
1) (пересечения операций и замкнутость объединения);
2) (пересечения операций и коммутативность объединения);
3) (пересечения операций и ассоциативность объединения);
4) (дистрибутивность операции объединения относительно операции пересечения);
(дистрибутивность операции пересечения относительно операции объединения);
5) ;
6) ;
7) ;
.
В случае, если для элементов множества выяснены пересечение и объединение , для которых выполняются отношения 1) ? 8), то тройка именуется булевой алгеброй. Так, в случае, если ? – семейство всех частей множества , то – булева алгебра.
Неспециализированные указания.
Изучить выше представленные теоретические положения и выполнить практическую часть работы.
Нижеприведенные примеры являются неспециализированными для всех вариантов.
Примеры
- Доказать справедливость взаимоотношений 1) ?
- Доказать принцип двойственности: C(A U B) = CA ? CB, C(A ? B) = CA U CB.
- Доказать равенства A U (A ? B) = A ? (A U B) = A.
- Доказать равенства:
CCА = А,
СJ = O,
CO =J.
- Доказать справедливость включения .
- Выяснить множества A U B, A ? B, A\B, B\A, A ? B, в случае, если:
а) A = {x: 0 x 2}, B = {x: 1 ? x ? 3};
б) A = {x: x2 — 3x 0}, B = {x: x2 — 4x + 3 ? 0};
в) A = {x: |x — 1| 2}, B = {x: |x — 1| + |x — 2| 3}. - Имеем
= 
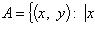
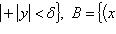
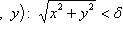
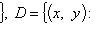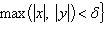. Продемонстрировать, что .
- Пускай A = {x: 2 ? x ? 4}, B = {y: 1 ? y ? 3}. Изобразить на плоскости ХOУ множество точек A ? B.
При невыполнения отдельных строений нужно представить настоящий процесс (попытку) получения результата и сформулировать вопрос (вопросы), непонимание которых стало причиной отрицательному результату.
Таблица вариантов
Следующее задание носит личный темперамент, и номер варианта
задания сходится с порядковым номером студента в издании группы. ??????????????????????????????????????????????????
Для заданных дискретных множеств {X} и {Y} (таблица 2) представить все указанные в таблице 1 множества. Множество {J}есть областью определения множеств {X} и {Y}.
Таблица 1
| J={1?30} | X?Y | CXY | CYX | X/Y | Y/X | X Y | X Y |
Таблица 2
| № Вар. | Множество Х по вариантам | |||||||||||||||||||
Таблица 3
| № Вар. | Множество У по вариантам | |||||||||||||||||||
Результаты исполнения разрешённого раздела оформить в наглядном, эргономичном для проверки виде, к примеру в форме таблицы.