Тема: операции над векторами. вычисление модуля и скалярного произведения

Цель: Формирование навыков исполнения операций над векторами и скалярного произведения и вычисления модуля векторов.

На исполнение практической работы отводится 2 часа.

Требования к исполнению практической работы:

1.Ответить на теоретические вопросы.

2.Оформить задания в тетради для практических работ.

Теоретический материал

Отрезок именуется направленным, в случае, если один из его финишей считается началом отрезка, а второй – его финишем.

Вектором именуется направленный отрезок. Вектор, заданной парой несовпадающих точек, обозначается знаком . Точка именуется началом, а точка — финишем вектора.

Расстояние | | именуется диной (модулем) вектора .

Вектор , финиши которого совпадают, именуется нулевым вектором. Протяженность нулевого вектора равна нулю.

Два вектора именуются коллинеарными, если они лежат на одной либо на параллельных прямых. Нулевой вектор считается коллинеарным любому вектору.

Скалярным произведением двух ненулевых векторов именуется число, равное произведению длин этих векторов на косинус угла между ними: .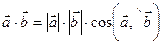

Скалярное произведение векторов и выражается через их координаты по формуле .

Угол между двумя векторами и находится по формуле .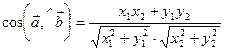

В случае, если отрезок разделен точкой в отношении , то координаты точки находятся по формулам

, .

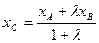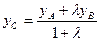В случае, если , то получаются формулы для нахождения координат середины отрезка:

, .

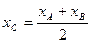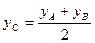Пример

Задание: Отрезок, финиши которого А(-11;1) и В(9;11), разделен в отношении 2:3:5 (от А к В). Отыскать точки деления.

Ответ: Обозначим точки деления от А к В через С и D. По условию , , , и АС:СD:DВ=2:3:5. тогда С дробит АВ в отношении 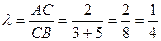; значит 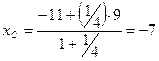; ; 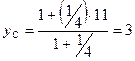так точка С имеет координаты (-7;3).

Точка D является серединой АВ, исходя из этого 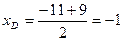; 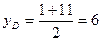. Тогда D(-1;6).

Задания для независимой работы

1. Отыщите координаты вектора , в случае, если , .
2. Точка дробит АВ в отношении 1:4 (от А к В). Отыщите точку А, в случае, если В(-6;-1).
3. Отыщите точку М, равноудаленную от осей координат и от данной точки А(4;-2).
4. Вычислите угол между векторами и .
5. Даны векторы , и . Выясните координаты вектора: а) ;

б) .

1. Отыщите скалярное произведение векторов и .
2. Вычислите и , в случае, если:

1) ;

2) ;

3) ;

4) .

1. Отыщите скалярное произведение векторов:

1) и ;

2) и ;

3) и ;

4) и .

Вопросы для самоконтроля:

1. Дайте определение вектора.

2. Что понимается под длиной либо модулем вектора?

3. Какие конкретно векторы именуются коллинеарными?

4. Что мы понимаем под произведением вектора на число?

5. Что именуется суммой векторов? Какие конкретно правила нахождения сумм векторов существуют?

6. Что именуется разностью двух векторов? Как выстроить разность двух векторов?

7. Дайте определение скалярного произведения двух векторов?

8. По какой формуле вычисляется скалярное произведение в координатах?

9. По какой формуле вычисляется угол между двумя векторами в координатах?

Практическое занятие №6

Тема: Составление кривых и уравнений прямых второго порядка, их построение

Цель: Формирование навыков кривых уравнений и составления прямых второго порядка, их построения

На исполнение практической работы отводится 2 часа.

Требования к исполнению практической работы:

1.Ответить на теоретические вопросы.

2.Оформить задания в тетради для практических работ.

Теоретический материал

Уравнение первой степени довольно переменных и , другими словами уравнение вида при условии, что коэффициенты и в один момент не равны нулю, именуется неспециализированным уравнением прямой.

Уравнение вида именуется векторным уравнением прямой. В случае, если его переписать в координатной форме, то окажется уравнение .

Каноническое уравнение прямой записывается в следующем виде 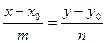, где и — координаты направляющего вектора прямой.

Уравнение прямой в отрезках на осях имеет форму 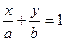, где и — соответственно ордината и абсцисса точек пересечения прямой с осями и .

Уравнение прямой с угловым коэффициентом имеет форму , где — угловой коэффициент, равный тангенсу угла наклона прямой к оси , а — ордината точки пересечения прямой с осью .

Уравнение прямой, проходящей через данную точку в заданном направлении, имеет форму , где — угловой коэффициент прямой.

Уравнение прямой, проходящей через две эти точки и , имеет форму 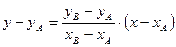. Угловой коэффициент прямой, проходящей через точки и , находится из соотношения .

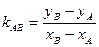Окружностью именуется множество точек плоскости, равноудаленных от данной точки данной плоскости, именуемой центром.

Уравнение окружности с центром в начале координат и радиусом имеет форму .

Уравнение окружности с центром в точке и радиусом имеет форму .

Уравнение окружности в общем виде записывается так: , где , , и — постоянные коэффициенты.

Эллипсом именуется множество точек плоскости, сумма расстояний которых до двух данных точек, именуемых фокусами, имеется величина постоянная , громадная расстояния между фокусами .

Уравнение эллипса, фокусы которого лежат на оси , имеет форму 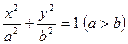, где — протяженность большей полуоси; — протяженность малой полуоси.

Преувеличением именуется множество точек плоскости, полная величина разности расстояний которых до двух данных точек, именуемых фокусами, имеется величина постоянная , меньшая расстояния между фокусами .

Уравнение преувеличения, фокусы которого лежат на оси , имеет форму 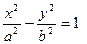, где — протяженность настоящей полуоси; — протяженность мнимой полуоси.

Параболой именуется множество точек на плоскости, равноудаленных от данной точки, именуемой фокусом, и от данной прямой, именуемой директрисой.

Уравнение параболы с вершиной в начале координат, осью симметрии которой помогает ветви и ось направлены вверх, имеет форму , где (параметр параболы) – расстояние от фокуса до директрисы. Уравнение ее директрисы .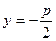

Пример

Задание 1: Выстроить прямую .

Ответ: Отыщем точки пересечения прямой с осями и .

Пускай .

Пускай .

Изобразим отысканные точки на координатной плоскости и соединим их, так, возьмём прямую заданную уравнением (рис. 1).

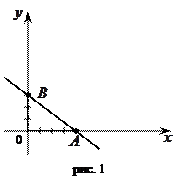Задание 2: Выстроить прямую .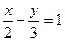

Ответ: Перепишем уравнение в виде: 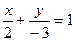, другими словами и . Так, приобретаем точки и , прямая проходящая через точки и есть искомой (рис. 2).

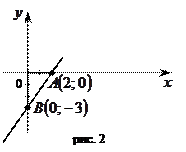Задание 3: Составить уравнение прямой, проходящей через точку и начало координат .

Ответ: Вектор коллинеарен искомой прямой. Для составления уравнения прямой используем каноническое уравнение прямой: 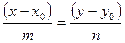. Так, подставив в данное уравнение , , , возьмём искомое уравнение прямой проходящей через точку и начало координат :

.

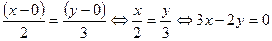Задание 4: Составить уравнение прямой, проходящей через данную точку и перпендикулярной данному вектору .

Ответ: Пускай — произвольная точка искомой прямой. Вектор перпендикулярен вектору . Так как векторы перпендикулярны, то их скалярное произведение равняется нулю, другими словами . Записав произведение этих векторов в координатной форме, возьмём:

. Уравнение искомой прямой имеет форму .

Задания для независимой работы

1. Проверить принадлежат ли точки , , и прямой .
2. Выстроить прямые:

1) ; 2) ; 3) ;

4) ; 5) ; 6) ;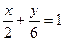

7) 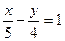; ; 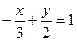9) .

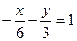1. Выстроить фигуру, ограниченную линиями , , и . Вычислить площадь данной фигуры.
2. Преобразуйте уравнения следующих прямых к уравнениям в отрезках на осях:

1) ; 2) ;

3) ; 4) ;

5) .

1. Составить уравнение прямой, проходящей через точку и начало координат : 1) ;

2) .

1. Составить уравнение прямой, проходящей через данную точку и перпендикулярной данному вектору :

1) ; ;

2) ; .

1. Составить уравнение окружности, проходящей через точки:

1) , , ;

2) , , ;

3) , , .

1. Составьте уравнение эллипса, в случае, если две его вершины находятся в точках и , а фокусы в точках и :

1) , , , ;

2) , , , ;

3) , , , .

Вопросы для самоконтроля:

1. Какое уравнение именуется неспециализированным уравнением прямой?

2. Какой вид имеет векторное уравнение прямой?

3. Какое уравнение именуется каноническим уравнением прямой?

4. Запишите уравнение прямой в отрезках на осях и уравнение прямой с угловым коэффициентом.

5. Какой вид имеют уравнения прямой, проходящей через данную точку в прямой и заданном направлении, проходящей через две эти точки?

6. Что именуется окружностью, эллипсом, преувеличением, параболой?

Практическое занятие №7

18+ Математика без Ху%!ни. Скалярное произведение векторов. Угол между векторами.

Интересные записи:

• Теория дешифрирования аэро- и космических снимков.
• Теория и практика разрешения конфликтов
• Теория конкурентоспособности наций м. портера
• Терапевтические условия для изменения личности