Широкое распространение он взял в изучении экономических явлений. Любой показатель, любая цифра, применяемая для оценки, прогноза и контроля, имеет значение лишь в сравнении с другими.
Сущность метода:
Сравнение – это научный способ, в ходе его малоизвестное (изучаемое) явление, предметы сопоставляются с уже известными, изучаемыми ранее, с целью определения неспециализированных линия или различий между ними.
Посредством сравнения определяется неспециализированное и своеобразное в экономических явлениях, изучаются трансформации исследуемых объектов, закономерности и тенденции их развития.
самые типичные обстановки, в то время, когда употребляется цели и сравнение, каковые наряду с этим достигаются:
1 Сопоставление плановых и фактических показателей для оценки степени исполнения замысла.
2 Сопоставление фактических показателей с нормативными разрешает совершить контроль за затратами и содействует внедрению ресурсосберегающих разработок.
3 Сравнение фактических показателей с показателями прошлых лет для определения тенденций экономических процессов.
4 Сравнение показателей разбираемого предприятия с достижениями передового опыта и науки работы вторых фирм (для поиска резервов).
5 Сравнение показателей разбираемого предприятия со средними по отрасли (для определения положения предприятия на рынке среди вторых фирм той же отрасли либо подотрасли).
6 Сопоставление параллельных и динамических последовательностей для изучения связей исследуемых показателей (К примеру: в один момент разбирая динамику трансформации количества производства валовой продукции, главных производственных фондов, фондоотдачи возможно и обосновать связь между этими показателями). Фо = СВП/ОПФ
Для этого показатели располагают в возрастающем либо убывающем порядке и разглядывают как поэтому изменяются другие показатели (возрастают либо убывают) и в какой степени.
7 Сопоставление разных вариантов управленческих ответов с целью выбора оптимального.
8 Сопоставление результатов деятельности до и по окончании трансформации какого-либо фактора (при подсчёте влияния резервов и подсчёте факторов).
Различают следующие виды сравнительного анализа: горизонтальный, вертикальный, трендовый, одномерный и многомерный.
Горизонтальный сравнительный анализ употребляется для определения безотносительных и относительных отклонений фактического уровня показателей от базисного (планового, прошлого периода, среднего уровня, передового опыта и достижений науки).
Вертикальный сравнительный анализ — изучается структура экономических процессов и явлений методом расчета доли, удельного веса в общем целом (соотношение частей главного и оборотного капитала, собственного и заемного).
Трендовый анализ используется при изучении относительных темпов прироста и роста показателей за последовательность лет к уровню базового года, другими словами при изучении последовательностей динамики.
Одномерный сравнительный анализ — сопоставляются один либо пара показателей одного объекта либо пара объектов по одному показателю.
Многомерный сравнительный анализ – проводится сопоставление результатов деятельности нескольких фирм (подразделений) по широкому спектру показателей.
Нужен для комплексной оценки результатов хозяйствования предприятия, подразделений и т.д.
Комплексная оценка хозяйственной деятельности предприятия – черта деятельности предприятия, полученная в следствии изучения совокупности показателей, каковые определяют большая часть экономических процессов и содержат обобщающие информацию о итогах производства. Чем больше показателей будет использовано для комплексной оценки, тем более верным будет вывод анализа.
2. МЕТОДЫ ПРИВЕДЕНИЯ ПОКАЗАТЕЛЕЙ В
СОПОСТАВИМЫ ВИД
Сравнивать возможно лишь как следует однородные размеры. Из этого следует необходимость обеспечения сопоставимости показателей.
Должны быть учтены следующие требования:
1 Единство объемных, стоимостных, структурных факторов.
2 Единство промежутков либо моментов времени, за каковые были исчислены сравниваемые показатели.
3 Сопоставимость исходных условий производства (технических, природных, климатических).
4 Единство их исчисления состава и методики показателей.
3. МЕТОД ОТНОСИТЕЛЬНЫХ И СРЕДНИХ РАЗМЕРОВ
Полные размеры показывают количественные размеры явления в единицах меры веса, количества, протяженности площади, и т.д безотносительно к размеру вторых явлений.
Относительные показатели отражают соотношение величины изучаемого явления с величиной какого-либо другого явления либо с величиной этого явления, но забранной за второе время либо По другому объекту. Относительные показатели получаются в следствии деления одной величины на другую, которая принимается за базу сравнения (база – замысел, базовый год, второе предприятие).
Относительные размеры эффективности – это отношение результата к ресурсам либо затратам (к примеру, производство продукции на 1 руб. затрат либо на одного рабочего).
Наровне с безотносительными и относительными показателями довольно часто используются средние величины.
Средние величины – используются для обобщенной чёрта совокупности однородных явлений по какому-либо показателю (средняя з/п отражает уровень зарплаты изучаемых работников).
Типы средних размеров:
Среднеарифметические (простые и взвешенные);
Среднегармонические;
Среднегеометрические;
Среднехронологические;
Среднеквадратические и др.
Средние величины дают обобщенную чёрта явлений, основываясь на массовых данных (скрывают результаты нехорошей работы отдельных подразделений предприятия)
При анализе появляется необходимость раскрывать содержание средних размеров, дополняя их среднегрупповыми, а время от времени и личными показателями.
4. МЕТОД ГРУППИРОВКИ ИНФОРМАЦИИ В ЭКОНОМИЧЕСКОМ АНАЛИЗЕ
Группировка информации — деление массы изучаемой совокупности объектов на как следует однородные группы по соответствующим показателям.
В зависимости от задач применяют типологические, структурные и аналитические группировки.
Типологические группировки – примером смогут быть группы предприятий по формам собственности, население по роду деятельности.
Структурные группировки – разрешают изучать внутреннее строение показателей, соотношения в нем отдельных частей. К примеру, изучение состава работников по стажу, профессиям, возрасту.
Аналитические (причинно-следственные) группировки – употребляются к примеру, для определения наличия связи между показателями. Аналитические группировки по характеру показателей смогут быть качественными (в то время, когда показатель не имеет количественного выражения) и количественные.
По сложности построения различают два типа группировок: простые и комбинированные. Посредством несложных группировок изучается связь между явлениями, сгруппированными по какому-либо одному показателю. В комбинированных группировках такое деление делается сперва по одному показателю, позже в каждой группы По другому показателю и т.д. Так, смогут быть выстроены двух-, трехуровневые группировки (для изучения сложных связей лучше такую группировку заменить несколькими несложными для лучшего восприятия).
5. БАЛАНСОВЫЙ МЕТОД В АФХД
Помогает для отражения соотношений двух групп взаимосвязанных и уравновешенных экономических показателей, итоги которых должны быть тождественными.
Данный способ употребляется при анализе обеспеченности предприятия трудовыми ресурсами, денежными ресурсами, сырьем, ОПФ и др., конечно при анализе полноты их применения (определяется фактическое наличие и потребность).
Как вспомогательное средство балансовый способ употребляется для проверки результатов расчетов влияния факторов на результативный показатель. В случае, если сумма влияния факторов на результативный показатель равна его отклонению от базисного значения, то, следовательно, расчеты совершены верно.
В некоторых случаях балансовый метод возможно использован для определения величины влияния отдельных факторов на прирост результативного показателя. К примеру, в то время, когда из трех факторов известно влияние двух, то влияние третьего возможно выяснить, забрав от общего прироста результативного показателя итог влияния первых двух факторов.
На базе балансового способа создан один из способов факторного анализа – долевого участия и пропорционального деления.
6. ГРАФИЧЕСКИЙ МЕТОД В АХД
График – масштабное изображение показателей, чисел посредством геометрических знаков (линий, прямоугольников, кругов).
Хорошая сторона метода – наглядность, более ясно проявляются связи и тенденции изучаемых показателей.
Главные формы графиков в АФХД – диаграммы.
Требования для построения графиков:
1. контрастность и Выразительность рисунка.
2. Масштаб, что снабжал бы наглядность и не усложнял его чтение.
3. Должен быть несложным и прекрасным.
7. ТАБЛИЧНЫЙ МЕТОД
Результаты анализа в большинстве случаев излагают в виде таблиц.
Аналитическая таблица – совокупность мыслей, суждений, выраженных языком цифр. Она значительно яснее и нагляднее текста.
Существует три вида таблиц: простые, групповые и комбинированные.
Простые таблицы – перечисляются единицы совокупности характеризуемого явления.
Групповые таблицы – эти по отдельным единицам изучаемой совокупности объединяются в группы по одному значительному показателю.
Комбинированные таблицы – материал разбивается на подгруппы и группы по нескольким показателям.
По аналитическому содержанию различают таблицы отражающие чёрта изучаемого объекта, порядок расчета показателей, динамику изучаемых показателей, изменения структуры в составе показателей, связь показателей по разным показателям, результаты расчета влияния факторов на уровень исследуемого показателя, методику подсчета резервов, сводные результаты анализа.
Требования к составлению таблиц:
1. Размещается таблица в тексте по окончании первого упоминания.
1. Таблица должна иметь заголовок, коротко отражающий содержание таблицы.
2. Непременно наличие единиц измерения.
3. Графы нумеруются, в случае, если в них приводится метод расчета.
4. По окончании таблицы пишут выводы: сперва неспециализированный результат, а после этого переходят к отдельным показателям.
5. Сперва приводят полные, позже относительные показатели.
8. ИНДЕКСНЫЙ СПОСОБ
Основывается на относительных показателях, высказывающих отношение уровня данного явления к уровню, забранному в качестве базы сравнения. Статистика именует пара видов индексов, каковые используются при анализе: агрегатные, арифметические, гармонически.
9. СПОСОБ КОРРЕЛЯЦИОННОГО И РЕГРЕССИОННОГО (СТОХАСТИЧЕСКОГО) АНАЛИЗА
Обширно употребляется для тесноты связи между показателями не находящимися в функциональной зависимости, другими словами сообщение проявляется не в каждом отдельном случае, а в определенной зависимости.
Посредством корреляции решаются две главные задачи:
— составляется модель действующих факторов (уравнение регрессии);
— дается количественная оценка тесноты связей (коэффициент корреляции).
10. МАТРИЧНЫЕ МОДЕЛИ
Это схематическое отражение экономического явления либо процесса посредством научной абстракции
11. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Это главное средство ответа задач по оптимизации производственно-хозяйственной деятельности.
12. СПОСОБ Изучения ОПЕРАЦИЙ
13. ТЕОРИЯ ИГР
МЕТОДИКА ФАКТОРНОГО АНАЛИЗА
1. ПОНЯТИЕ, ЗАДАЧИ и ТИПЫ ФАКТОРНОГО АНАЛИЗА
Под факторным анализом понимается методика комплексного и измерения воздействия и системного изучения факторов на величину результативных показателей.
Различают следующие типы факторного анализа
1. Детерминированный факторный анализ – методика изучения влияния факторов, сообщение которых с результативным показателем носит функциональный темперамент, другими словами в то время, когда результативный показатель представлен в виде произведения, частного либо алгебраической суммы факторов.
2. Стохастический анализ – методика изучения факторов, сообщение которых с результативным показателем в отличие от функциональной есть неполной, вероятностной (корреляционной).
3. Прямой факторный анализ – изучение ведется дедуктивным методом — от общего к частному.
4. Обратный факторный анализ – метод логической индукции – от частных факторов к обобщающим.
5. Одноступенчатый – употребляется для изучения факторов лишь первого уровня подчинения без их детализации на составные части К примеру, у=а +в (разложение на а и в).
6. Многоступенчатый факторный анализ – проводится детализация факторов (а и в) на составные элементы с целью изучения их поведения.
7. Статистический факторный анализ – изучение влияния факторов на результативные показатели на соответствующую дату.
8. Динамический факторный анализ – методика изучения причинно-следственных связей в динамике.
9. Ретроспективный – изучает обстоятельства прироста результативных показателей за прошлые периоды.
10. Перспективный – исследует поведение результативных показателей и факторов в возможности.
Главные задачи факторного анализа:
1 Отбор факторов, определяющих исследуемые результативные показатели.
2 систематизация и Классификация факторов для обеспечения комплексного и системного подхода к изучению их влияния на результаты хозяйственной деятельности.
3 Определение формы зависимости между результативным показателем и факторами.
4 Моделирование связей между результативными и факторными показателями.
5 оценка влияния роли и Расчёт факторов каждого из них в трансформации величины результативного показателя.
6 Работа с факторной моделью (практическое ее применение для управления экономическими процессами).
ТИПЫ и МОДЕЛИРОВАНИЕ ФАКТОРНЫХ МОДЕЛЕЙ
Одной из задач факторного анализа есть моделирование связей между факторами и результативными показателями, каковые определяют их величину.
Моделирование — один из наиболее значимых способов научного познания, благодаря которому создается модель (условный образ) объекта изучения.
Сущность моделирования – связь исследуемого показателя с факторными представлена в виде математического уравнения.
В факторном анализе различают модели детерминированные (функциональные) и стохастические (корреляционные).
Посредством детерминированных факторных моделей исследуется функциональная связь между факторами и результативным показателем, посредством стохастических факторных моделей устанавливается вероятностная (неполная) сообщение.
В детерминированном анализе выделяют следующие типы факторных моделей:
1 Аддитивная модель – результативный показатель представляет собой алгебраическую сумму (отличие) нескольких факторных показателей.
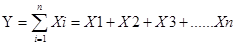
К таким моделям относятся показатели себестоимости во связи с статьями и элементами затрат на производство. Количество производства продукции во связи с количеством выпуска отдельных изделий.
2. Мультипликативные модели – результативный показатель является произведением нескольких факторов.
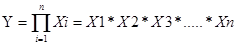
Примером мультипликативной модели есть двухфакторная модель количества производства продукции: ВП = ЧР(числ.раб.) * ГВ(выраб. 1 раб.)
3. Кратные модели – результативный показатель приобретают делением одного факторного показателя на величину другого.
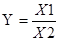
Примером кратной модели помогает коэффициент оборачиваемости оборотных средств: Коб = ДВ / об.ср.
4. Смешанные (комбинированные) модели – сочетание в разных комбинациях прошлых моделей.
; 
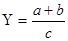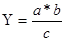; У = (а+б)*с
Примером может служить показатель: затраты на 1 руб. валовой продукции – Затр/ЧР *ГВ, показатели рентабельности.
Моделирование факторных совокупностей:
Для изучения зависимости между показателями и количественного измерения множества факторов, повлиявших на результативный показатель применяют преобразование моделей с целью включения новых факторных показателей.
1 Моделирование аддитивных факторных совокупностей – расчленение одного либо нескольких факторных показателей на составные элементы.
СТП = СВП – Незавершенное производство.
2.Моделирование мультипликативных факторных совокупностей – последовательное расчленение факторов исходной совокупности на факторы сомножители.
ВП = ЧР (числ. Раб.) * ГВ(выраб. 1 раб.)
ВП = ЧР * Д(кол-во дней) * ДВ (дневн. выраб.)
ВП = ЧР * Д * П(прод. раб. Дня) * ЧВ(часов.выраб.)
3. Моделирование кратных факторных совокупностей – преобразование методом удлинения, формального разложения, расширения, сокращения.
А) Первый способ – удлинение числителя методом замены одного либо нескольких факторов на сумму однородных показателей.
К примеру себестоимость единицы продукции:
Сед. = Затр./ВП
Сед. = ОТ + Опытен. Затр. + Амортиз …./ВП
По окончании замены неспециализированной суммы затрат отельными их элементами приобретаем аддитивную модель с новым комплектом факторов: Сед. = Отед. + МЗед. + Аморт.ед. …
На себестоимость единицы продукции воздействуют факторы – трудоемкость, материалоемкость, фондоемкость и пр.
Б) Метод формального разложения — удлинение знаменателя методом замены одного либо нескольких факторов на сумму либо произведение однородных показателей.
У = А/В
В = Л + М + Н
У = А / Л + М + Н
Приобретаем модель для того чтобы же вида, что и исходная.
К примеру, рентабельность производства: Р = Пр/ Сс = Пр/ ОТ + МЗ + Ам …
В) Способ расширения – расширение исходной модели за счет знаменателя дроби и умножения числителя на один либо пара новых показателей.
А А * С А С
У = ——- = ———— = ——— * ——— = Х1 * Х2
В В * С С В
В следствии оказалась новая мультипликативная модель в виде произведения нового комплекта факторов.
К примеру, среднегодовая выработка продукции одним работником (производительность труда), в случае, если ввести показатель Д — количество отработанных дней всеми работниками, будет иметь вид:
ВП ВП * Д ВП Д
ГВ = ——— = ———— = —— * —— = ДВ * Д
ЧР ЧР * Д Д ЧР
ДВ * Д = среднедневная выработка всеми работниками * количество отработанных дней одним работником
По окончании введения показателя Т – количество отработанных часов всеми работниками, возьмём модель с новым комплектом факторов:
ВП * Д * Т ВП Д Т
ГВ = —————— = —— * —- * —— = ЧВ * Д * П
ЧР * Д * Т Т ЧР Д
ЧВ * Д * П = среднечасовая выработка * количество отработанных дней одним работником * длительность рабочего дня.
Г) Метод сокращения создание новой факторной модели методом знаменателя дроби и деления числителя на одинаковый показатель.
А А : С Х1
У = ——— = ——— = ——
В В : С Х2
К примеру, Фо = ВП / ОПФ, поделим знаменатель и числитель на среднегодовое количество работников:
ВП : ЧР ГВ ( годовая выработка одним работником)
Фо = ————— = ————————————————————
ОПФ : ЧР Фв (фондовооруженность)
На практике для преобразования одной и той же модели возможно последовательно использовано пара способов:
СРП Пр + Сс Пр Сс Пр Об.ср. Сс
Фо = ——- = ————- = —— + —— = —— + ——- * ——
ОПФ ОПФ ОПФ ОПФ ОПФ ОПФ Об.ср.
В этом случае для преобразования использованы расширения и способы удлинения. Полученная модель разрешает изучить влияние на фондооотдачу следующих факторов: рентабельность главных средств, соотношение между главными и оборотными средствами, коэффициент оборачиваемости оборотных средств.
4 МЕТОДЫ ИЗМЕРЕНИЯ ВЛИЯНИЯ ФАКТОРОВ В ДЕТЕРМИНИОВАННОМ АНАЛИЗЕ
Метод цепной подстановки.
Употребляется для расчета влияния факторов во всех типах детерминированных факторных моделей.
Метод разрешает выяснить влияние отдельных факторов на трансформацию величины результативного показателя методом постепенной замены базовой (плановой) величины каждого факторного показателя в количестве результативного показателя на фактическую (отчетную) в отчетном периоде.
Для этого определяют последовательность условных размеров результативного показателя, каковые учитывают изменение первых, после этого вторых и третьих и т.д. факторов, допуская, что остальные неизменны. Сравнение величины результативного показателя до и по окончании трансформации уровня того либо другого фактора разрешает элиминироваться (избежать, отклониться) от влияния всех факторов, не считая одного, и выяснить действие последнего на прирост результативного показателя.
Индексный способ
Индексный способ основан на относительных показателях динамики, пространственных сравнений, исполнения замысла, высказывающих отношение фактического уровня разбираемого показателя в отчетном периоде к его уровню в базовом (либо к плановому, либо По другому объекту).
Посредством агрегативных индексов возможно распознать влияние разных факторов на трансформацию уровня результативных показателей в мультипликативных и кратных моделях.
К примеру:
Индекс цены товарной продукции (ТП):
Iтп =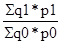 
Он отражает трансформации физического количества товарной продукции (q) и стоимостей (р) и равен произведению этих индексов:
Iтп = Iq * Ip =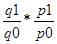 
Дабы установить, как изменилась цена товарной продукции за счет количества произведенной продукции и за счет стоимостей, необходимо вычислить индексы физического количества Iq и стоимостей Ip.
Iq (количества) =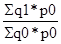 
Ip (стоимостей) =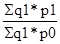 
В примере количество валовой продукции (ВП) возможно представить в виде произведения численности рабочих (ЧР) и их среднегодовой выработки одним работником (ГВ).
Iвп = Iчр * Iгв
Iвп =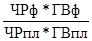 
Чрф * ГВф – ЧРп* ГВп = общ. изм. ВП
Iчр =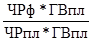 
ЧРф *ГВп – ЧРп * ГВп = изм. ВП за счет ЧР
Iгв =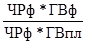 
ЧРф * ГВф – ЧРф * ГВп = изм.ВП за счет ГВ
В случае, если из числителя этих формул вычесть знаменатель, возьмём безотносительные приросты валовой продукции в целом и за счет каждого фактора, другими словами те же результаты, что и методом цепной подстановки.
3 Метод полных отличий
Метод полных отличий есть одной из модификаций элиминирования.
Используется для расчета влияния факторов на прирост результативного показателя в детерминированном анализе, но лишь в мультипликативных и мультипликативно-аддитивных моделях:
У = (а – в) *с и У = а * (в – с)
При его применении величина влияния факторов рассчитывается умножением полного прироста исследуемого фактора на базисную (плановую) величину факторов, каковые находятся справа от него и на фактическую (отчетную) величину факторов, расположенных слева от него в модели.
Расчет строится на последовательной замене плановых (базовых) значений факторных показателей на их отклонения, а после этого на фактический (отчетный) уровень этих показателей.
Метод относительных отличий
Метод используется для измерения влияния факторов на прирост результативного показателя лишь в мультипликативных и аддитивно-мультипликативных моделях типа:
У = (а – В) * с
Для расчета влияния 1-го фактора нужно базовую (плановую) величину результативного показателя умножить на относительный прирост 1-го фактора, выраженного в процентах, и итог поделить на 100.
Дабы вычислить влияние 2-го фактора, необходимо к плановой величине результативного показателя прибавить изменение его за счет 1-го фактора и взятую сумму умножить на относительный прирост 2-го фактора в процентах и итог поделить на 100 и т.д.
Влияние 3-го фактора: к плановой величине результативного показателя нужно прибавить изменение его за счет 1-го фактора прибавить изменение его за счет 2-го фактора и взятую сумму умножить на относительный прирост 3-го фактора в % и итог поделить на 100.
Интегральный метод
Элиминирование как метод детерминированного факторного анализа имеет значительный недочёт.
При его применении исходят из того, что факторы изменяются независимо друг от друга.
На самом же деле они изменяются совместно, взаимосвязано и от этого сотрудничества получается дополнительный прирост результативного показателя, что при применении способов элиминирования присоединяется к одному из факторов, в большинстве случаев, к последнему.
Поэтому величина влияния факторов на трансформацию результативного показателя изменяется в зависимости от места, на которое поставлен тот либо другой фактор в детерминированной модели.
Избавиться от этого недочёта допустимо применяя интегральный способ.
Способ используется для измерения влияния факторов в мультипликативных, кратных и смешанных моделях кратно-аддитивного вида:
У = А / Хi
Применение этого метода разрешает приобретать более правильные результаты расчета влияния факторов по сравнению со методами цепной подстановки, полных и относительных отличий.
В интегральном способе пользуются определенными формулами.
1. F = XY
Fx = XУo /2 X Y либо Fx = 1/2 X(Yo + Y1)
Fy = YХo + 1/2 X Y либо Fy = 1/2 Y(Xo +X1)
2. F = XYZ
Fx = 1/2 X(YoZ1 + Y1Xo) + 1/3 X Y Z
Fy = 1/2 Y(XoZ1 + X1Zo) + 1/3 X Y Z
Fz = 1/2 Z(XoY1 + X1Yo) + 1/3 X Y Z
Для расчета влияния факторов в смешанных моделях и кратных употребляются следующие рабочие формулы.
1. Вид модели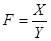 
;
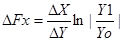К примеру:
ГВ = ВП/ЧР ГВп = 160000/1000 = 160 ГВф = 240000/1200 = 200
80000 1200
вп = ———— ln ——— = 400 ln 1,2 = 400 * 0,182 = + 73
200 1000
чр = (200 – 160) – 73 = 40 – 73 = -33
2 Вид факторной модели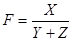 
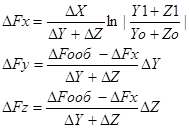
1. Вид факторной модели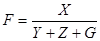 
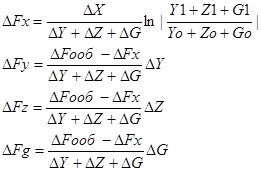
Применение интегрального способа не требует знания всего процесса интегрирования. Достаточно в готовые рабочие формулы подставить нужные числовые эти и сделать не сверхсложные расчеты посредством калькулятора. Наряду с этим достигается более высокая точность расчетов.