Смешанным произведением векторов `а,`b,`с именуют скалярное произведение вектора `а ´`b на вектор `с, т.е. `а`b`с = (`а ´`b)`с(1.23)
Свойства смешанного произведения:
1) смешанное произведение равняется нулю, в случае, если:
а) хоть один из перемножаемых векторов равен нулю;
б) два из перемножаемых векторов коллинеарны;
в) перемножаемые векторы компланарны.
2) смешанное произведение не изменится, в случае, если символы векторного и скалярного произведения поменять местами, т.е (`а ´`b)`с = `а (`b ´`с).
3) смешанное произведение не изменяется, в случае, если перемножаемые векторы переставлять в круговом порядке: `а `b`с = `b`с`а = `с`а `b
4) при перестановке двух любых векторов смешанное произведение меняет символ: `b`а `с = –`а `b`с ; `с `b`а = –`а `b`с; `а `с`b = –`а `b`с
В случае, если векторы заданы собственными координатами, то: 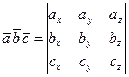 (1.24)
(1.24)
| Условие компланарности векторов принимает вид: | 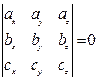
|
(1.25) |
(Компланарные вектора параллельны одной плоскости; векторное произведение двух векторов даст вектор, перпендикулярный данной плоскости и третьему вектору и их скалярное произведение будет равняется нулю).
Количества призмы V1 и пирамиды V2 выстроенных на `а,`b,`с определятся так: V1 = |`а `b`с| и V2 = 1 / 6 |`а `b`с | (1.26).
Тесты
1. Даны три вектора = (1; 2; -1); = (-2; 1; 3) и = (3; -1; 2). Смешанное произведение равняется:
1) –32; 2) 14; 3) 48; 4) 32.
2. Даны точки А (3; 1; -1), В (0; 2; -4), С (-2; 1; 3) и Д (-5; 0; 7). Количество пирамиды АВСД численно равен:
1) 8; 2) 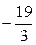 ; 3) ; 4) –8.
; 3) ; 4) –8.
3. Какие конкретно из векторов = (3; 1; -2); = (7; -3; 2); = (3; -7; 8), = (1; -1; 1) компланарны:
1) ; 2) ; 3) ; 4) .
4. Два соседних вектора в смешанном произведении поменяли местами. Что правильно?
1) = ; 2) = — .
5. Векторы = (1; 2; 3), = (3; 4; 5) и = (5; 6; Х). Х =
1) –7; 2) –8; 3) 7; 4) 8.
5.5 собственные векторы и Собственные значения матрицы.Характеристическим уравнением матрицы 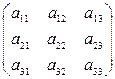 именуют уравнение
именуют уравнение 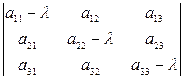 = 0 (1.27)
= 0 (1.27)
Корни этого уравнения именуют характеристическими числами (собственными значениями) матрицы.
Совокупность уравнений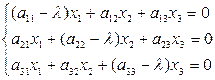 , в которой l имеет одно из значений и определитель которой поэтому равен нулю, определяет тройку чисел (х1, х2, х3), соответствующую данному характеристическому числу. Эта совокупность чисел с точностью до постоянного множителя определяет ненулевой вектор , именуемый собственным вектором матрицы. Так, квадратная матрица 3-его порядка имеет три собственных значения и три собственных вектора. (В общем случае среди собственных значений смогут быть и кратные (однообразные), среди них и комплексные и мнимые. Личные значения симметрической матрицы- лишь настоящие числа.) Векторы эти смогут быть записаны в матричной форме, в виде вектора-столбца, где t– произвольное постоянное
, в которой l имеет одно из значений и определитель которой поэтому равен нулю, определяет тройку чисел (х1, х2, х3), соответствующую данному характеристическому числу. Эта совокупность чисел с точностью до постоянного множителя определяет ненулевой вектор , именуемый собственным вектором матрицы. Так, квадратная матрица 3-его порядка имеет три собственных значения и три собственных вектора. (В общем случае среди собственных значений смогут быть и кратные (однообразные), среди них и комплексные и мнимые. Личные значения симметрической матрицы- лишь настоящие числа.) Векторы эти смогут быть записаны в матричной форме, в виде вектора-столбца, где t– произвольное постоянное
число. 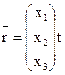 (1.28) (1.28) |
(Обычно его эргономичнее применять, чем уже привычный вектор-строчок). |
Пример: Отыскать собственные векторы и собственные значения матрицы: 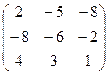 . Характеристическое уравнение матрицы примет вид:
. Характеристическое уравнение матрицы примет вид: 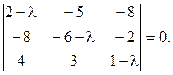 Раскроем определитель по элементам первой строки
Раскроем определитель по элементам первой строки 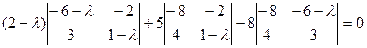
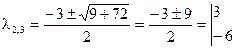
Сейчас возможно отыскать личные векторы матрицы
I. 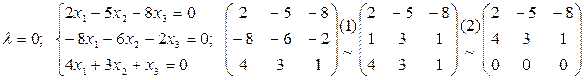
Применяя (1.10) отыщем 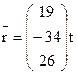
II. 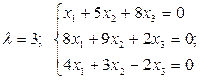
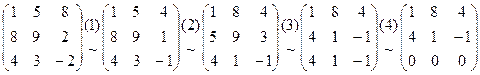
(1) — поделим 3-ий столбец на 2, (2) — заменим строки столбцами, (3) — вычтем из 2-ой строки 1-ую, (4 — вычтем из 3-ей строки 2-ую, применяя (1.10) отыщем: .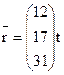
III. Подобно вычисляется личный вектор и для .
Тесты
1. Характеристическим уравнением матрицы А= 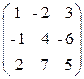 именуют уравнение:
именуют уравнение:
1) 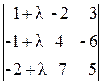 =0; 2)
=0; 2) 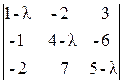 =0; 3)
=0; 3) 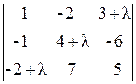 =0.
=0.
2. Дана матрица А= 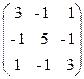 , ее характеристические числа:
, ее характеристические числа:
1) 2; -3; -6; 2) –2; -3; 6; 3) 2; 3; 6; 4) –2; -3; -6.
3. А = 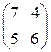 личные векторы равны:
личные векторы равны:
1) (1; 1); 2) (1; -1); 3) (-1; 1); 4) (4; -5).
4. А = 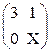 ; Личные значения матрицы:
; Личные значения матрицы:
1) (Х; 3); 2) (Х; Х); 3) (3; 3).
5. Дана диагональная матрица А = 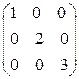 ; Возможно ли утверждать, что = t(1; 2; 3) – личный вектор?
; Возможно ли утверждать, что = t(1; 2; 3) – личный вектор?
1) Да; 2) Нет.
5.6. Линейные (векторные) пространства. Линейные преобразования. Квадратичные формы.
Разглядим множество R элементов x, y, z,… для любых и которого выяснена сумма х+у и для любого настоящего числа выяснено произведение
В случае, если эти операции удовлетворяют условиям:
1. х+у = у+х ;
2. х+(у+z) = (x+y)+z;
3. Существует таковой элемент , (нуль- элемент) что х+0 = х для любого ;
4. Для каждого существует таковой, что х+у = 0 (у = —х, т.е. х+(-х) =0);
5. ;
6.
7.
8.
то множество именуют линейным (либо векторным) пространством, а его элементы x, y, z,…- векторами.
Разумеется, что множество геометрических векторов, рассмотренное ранее, есть линейным пространством, а предложенное определение расширяет понятие вектора.
Линейная независимость векторов определяется через соотношение (1.15), рассмотренное ранее. Предельное количество n линейно свободных векторов именуют размерностью этого пространства (обозначение: ) — его именуют n-мерным и обозначают Rn (разглядываем конечномерные пространства). Каждые n линейно свободных векторов в пространстве Rn образуют базис в этом пространстве. По векторам базиса возможно единственным образом разложить любой вектор пространства.
Линейные преобразования.
Говорят, что в линейном пространстве R задано преобразование А, в случае, если каждому вектору по некоему правилу ставится в соответствие вектор А . Преобразование именуют линейным, в случае, если для любых х и у и любого настоящего числа выполняются равенства А(х+у)=Ах+АуиА( х)= Ах (его возможно разглядывать как линейное преобразование координат точки либо вектора- переход к вторым координатам). Пускай в пространстве R3 с базисом задано линейное преобразование А. Любой из векторов возможно единственным образом разложить по векторам базиса
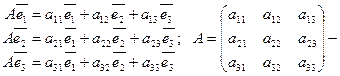 матрица линейного преобразования А в базисе . (подобно — в пространстве при ).
матрица линейного преобразования А в базисе . (подобно — в пространстве при ).
Действия над линейными преобразованиями сводятся к действиям над их матрицами. К примеру, в случае, если вектор переводится в вектор преобразованием А, а вектор переводится в вектор преобразованием В, это равносильно преобразованию С, переводящему вектор в вектор (его именуют произведением составляющих преобразований).
Матрица этого линейного преобразования С = ВА.
Пример: Даны два линейных преобразования
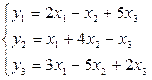 и
и 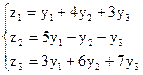 либо
либо 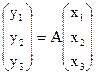 и
и 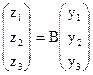 , где
, где 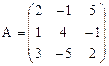 и
и 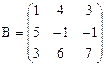
Искомое преобразование С определится произведением А и В
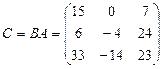 и
и 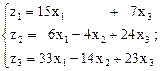
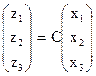 .
.
Вид матрицы линейного преобразования определяется выбором базиса. В случае, если за базис принять совокупность собственных векторов (см. 1.5.5), то матрица линейного преобразования принимает диагональный вид, причём на основной диагонали стоят личные значения. К примеру, в R2 это матрица 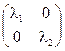 , линейное преобразование:
, линейное преобразование: 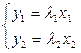 .
.
Квадратичные формы.
Квадратичной формой переменных х1, х2,…,хn именуют многочлен второй степени довольно этих переменных, не содержащий участников нулевой и первой степени.
При n=2
при n=3
А = 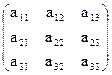 , где aij = aji именуют матрицей квадратичной формы . Матрица А симметрическая, личные значения её- настоящие числа.
, где aij = aji именуют матрицей квадратичной формы . Матрица А симметрическая, личные значения её- настоящие числа.
Пускай 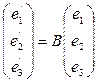 нормированные личные векторы в ортонормированном базисе е1, е2,е3. Векторы кроме этого образуют ортонормированный базис.
нормированные личные векторы в ортонормированном базисе е1, е2,е3. Векторы кроме этого образуют ортонормированный базис. 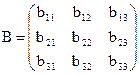 — матрица перехода о т базиса е1,е2,е3 к базису . Формулы преобразования координат при переходе к новому ортонормированному базису примут вид:
— матрица перехода о т базиса е1,е2,е3 к базису . Формулы преобразования координат при переходе к новому ортонормированному базису примут вид: 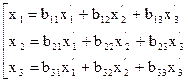
Переходя к новым координатам приобретаем квадратичную форму не содержащую участников с произведениями переменных. Квадратичная форма приведена к каноническому виду посредством ортогонального преобразования. (Предполагалось, что среди собственных чисел матрицы А нет кратных. В случае, если они имеется, задача решается мало сложнее).
Пример: Привести к каноническому виду уравнение линии 17х2+12ху+8у2=80. В левой части — квадратичная форма с матрицей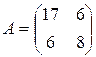 . Отыщем личные значения:
. Отыщем личные значения: 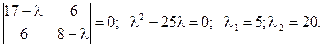 Матрица преобразования принимает вид
Матрица преобразования принимает вид 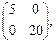 квадратичная форма преобразуется к канонической, а уравнение линии к виду либо
квадратичная форма преобразуется к канонической, а уравнение линии к виду либо 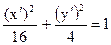 — (каноническое уравнение эллипса).
— (каноническое уравнение эллипса).
Тесты
1. Даны две совокупности четырех настоящих чисел: I (а; в; 0; 0), (с; d; 0; 0), (е; f; 0; 0) и II (а; в; 1; 1), (с; d; 1; 1), (е; f; 1; 1). (авсd – всевозможные настоящие числа). есть хоть одна из них (в случае, если да, то какая) линейным пространством?
2. В линейном пространстве с базисом , дано линейное преобразование А. Какова матрица обратного преобразования А-1, в случае, если А = , А = ?
1) 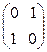 ; 2)
; 2) 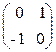 ; 3)
; 3) 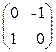 ; 4)
; 4) 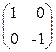 .
.
3. Каноническая форма уравнения линии 4xy + 3y2 + 16 = 0 имеет форму:
1) 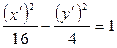 ; 2)
; 2) 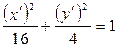 ; 3)
; 3) 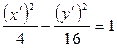 .
.
Линия на плоскости. Прямая.
Любая линия на плоскости является совокупностью точек. В случае, если известно аналитическое соотношение (формула), связывающее координаты любой (текущей) точки М(х,у), лежащей на данной линии, говорят – линия задана своим уравнением у = f (x) (в общем случае F(x,y) = 0).
В случае, если в уравнение линии подставить координаты любой ее точки, то уравнение обратится в тождество.
Всякое уравнение первой степени (линейное) довольно х и у вида
Ах + Ву + С = 0 (1.29),
(А, В, С – постоянные размеры, причем А2+ В2 ¹ 0) определяет на плоскости некую прямую и именуется неспециализированным уравнением прямой. Разглядим частные случаи:
1. А ¹ 0, В ¹ 0, С = 0. Разумеется, что Ах + Ву = 0 – уравнение прямой проходящей через начало координат.
2. А = 0, В ¹ 0, С ¹ 0. Уравнение (1.29) преобразуется к виду у = – С / В = b и определяет прямую параллельную оси Ох (При С = 0 = b = 0 и прямая сходится с осью Ох)
3. А ¹ 0, В = 0, С ¹ 0. Уравнение (1.29) принимает вид х = – С /А = а и определяет прямую параллельную оси Оу (При С = 0 = a = 0 и прямая сходится с осью Оу)
4. В случае, если В ¹ 0, то, разрешив (1.29) довольно у, возьмём уравнение вида
у = кх + b (1.30)
(к = – А / В, b = – С / В), именуемое уравнением с угловым коэффициентом, (к = tga, где a – угол между прямой и хорошим направлением оси Oх. b – ордината точки пересечения прямой с осью Оу).
5. В случае, если в (1.29) С ¹ 0, то поделив обе части равенства на -С, возьмём уравнение вида (х / а) – (у / b) = 1 (1.31)
( а = – С/А; b = – С/В, именуемое уравнением прямой в отрезках (|a| и|b| – длины отрезков, отсекаемых на осях Ох и Оу от начала координат).
6. Умножив обе части (1.29) на 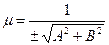 (нормирующий множитель, символ которого выбирают из условия m С 0) возьмём обычное уравнение прямой х соs j + y sin j – p = 0 (1.32),
(нормирующий множитель, символ которого выбирают из условия m С 0) возьмём обычное уравнение прямой х соs j + y sin j – p = 0 (1.32),
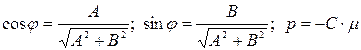 ,гдер – протяженность перпендикуляра, опущенного из начала координат на прямую, а j – угол между ним и осью Ох.
,гдер – протяженность перпендикуляра, опущенного из начала координат на прямую, а j – угол между ним и осью Ох.
Применяя предложенные формы уравнений прямой возможно взять следующие соотношения:
Острый угол между прямыми у = к1х + b1, у = к2х + b2, определится по формуле: 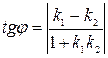 (1.33)
(1.33)
Из нее легко взять условие параллельности к1 = к2 (1.34)
и перпендикулярности к2 = – 1 / к1 (1.35) прямых.
Уравнение прямой, проходящей через точку М0(х0, у0) под заданным углом aк оси Ох (с заданным угловым коэффициентом к = tga) примет вид
у – у0 = к (х – х0) (1.36),
а уравнение прямой, проходящей через заданные точки М1(х1, у1) и М2(х2, у2).
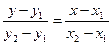 (1.37)
(1.37)
Отыскать координаты точки пересечения прямых возможно решив совокупность уравнений, определяющих эти прямые.
Расстояние от точки М0(х0, у0) до прямой Ах + Ву + С = 0 определяется по формуле: 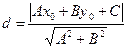 (1.38)
(1.38)
Деление отрезка в данном отношении. Приведем еще одно соотношение, довольно часто применяемое в аналитической геометрии. Совершим прямую через точки А(х1, у1)иВ(х2, у2). Любая третья точка С(х, у) прямой дробит отрезок АВ в некоем отношении l = ± АС / СВ (в случае, если точка С лежит в отрезка АВ, то l 0, в случае, если вне, то l 0). Координаты точки С определяются выражениями:
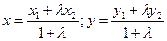 (1.39) (l = 1, в случае, если точка С – середина отрезка).
(1.39) (l = 1, в случае, если точка С – середина отрезка).
Тесты
1. Неспециализированное уравнение прямой имеет форму:
1) ;
2) (А2+В2¹0);
3) y = kx + в;
4) 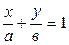 .
.
2. Угол между прямыми определяется выражением:
1) 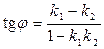 ; 3)
; 3) 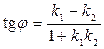 ;
;
2) 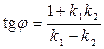 ; 4)
; 4) 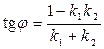 .
.
3. Условия перпендикулярности прямых:
1) ; 2) ; 3) 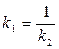 ; 4)
; 4) 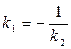 .
.
4. Уравнение прямой проходящей через данную точку М (х0, y0) с заданным угловым коэффициентом имеет форму:
1) y – y0 = k (x + x0);
2) y – y0 = k (x — x0);
3) y – х0 = k (x — у0);
4) y0 – х0 = k (у — x).
5. Уравнение прямой, проходящей через точки А(2; -3) и B(-2; 3) имеет форму:
1) 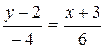 ; 2)
; 2) 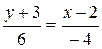 ; 3)
; 3) 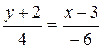 .
.
Кривые второго порядка.
Неспециализированное уравнение кривой второго порядка на плоскости хОуимеет вид
Ах2 + Вху + Су2 + 2Дх + 2Еу + F = 0 (1.40)
(Порядок кривой определяется наивысшей степенью малоизвестных, входящих в ее уравнение). Возможно продемонстрировать, что это уравнение обрисовывает или две пересекающиеся прямые, или одну из следующих кривых: эллипс, преувеличение либо параболу (включая вырожденные случаи). В любом случае кривую возможно выяснить как геометрическое место точек, владеющих некоторым неспециализированным свойством. Применяя преобразование координат (изменяя размещение кривой по отношению к осям координат) возможно сделать так, дабы в новых координатах уравнение кривой принимало самая простую и удобную для анализа форму. Разглядим последовательно кривые, конкретно так расположенные на плоскости хОу.
Эллипс. Окружность.
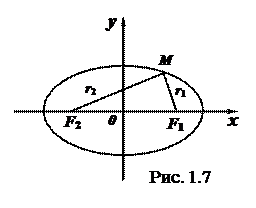 Эллипсом именуют множество (геометрическое место) точек, суммы расстояний которых до двух данных точек, именуемых фокусами, имеется величина постоянная (ее обозначают через 2а), причем эта величина больше расстояния между фокусами (его обозначают через 2с).
Эллипсом именуют множество (геометрическое место) точек, суммы расстояний которых до двух данных точек, именуемых фокусами, имеется величина постоянная (ее обозначают через 2а), причем эта величина больше расстояния между фокусами (его обозначают через 2с).
В случае, если фокусы эллипса размещаюся на оси Ох симметрично началу координат в точках F1(c, 0) и F2 (-c, 0) (рис.1.7), то уравнение эллипса примет несложную (каноническую) форму: 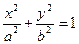 (1.41)
(1.41)
где а и b – громадная и малая полуоси эллипса, причем а, b, с связаны соотношением а2 = b2 + с2. Форма эллипса (мера сжатия) характеризуется эксцентриситетом 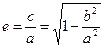 (1.42).
(1.42).
Разумеется, что 0 ? е ? 1; е = 1при b = 0 и эллипс вырождается в отрезок длиной 2а; е = 0при b = очень плохо, в то время, когда эллипс вырождается в окружность радиуса а.
Расстояния произвольной точки М(х, у) эллипса от его фокусов именуются фокальными радиусами – векторами данной точки, обозначаются r1 и r2 и смогут быть вычислены по формулам r1 = а – ех (1.43) (правый радиус – вектор) и r1 = а + ех (1.43`) (левый радиус – вектор).
При е = 0 (а = b = r) уравнение примет вид х2 + у2 = r2 (1.44)
Это уравнение окружности – геометрического места точек равноудаленных от данной точки, именуемой центром (в ней «сошлись» фокусы эллипса), с центром в начале координат. Уравнение окружности с центром в заданной точке С(а, b) примет вид (х – а)2 + (у – b)2 = r2 (1.44`)
Преувеличение. Преувеличением именуется геометрическое место точек, полная величина разности расстояний которых до двух данных точек, именуемых фокусами, имеется величина постоянная (ее обозначают через 2а),
 причем эта величина меньше расстояния между фокусами (ее обозначают через 2с).
причем эта величина меньше расстояния между фокусами (ее обозначают через 2с).
В случае, если фокусы преувеличения расположены на оси Ох симметрично началу координат в точках F1(с, 0) и F2(–с, 0), уравнение преувеличения примет каноническую форму
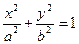 (1.46), причем b2 = c2 – a2 (1.47).
(1.46), причем b2 = c2 – a2 (1.47).
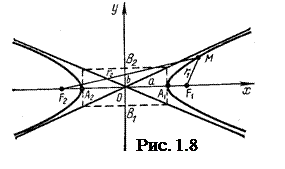
Преувеличение складывается из двух ветвей и расположена симметрично относительно осей координат. Точки А1(а, 0) и А2(–а, 0) именуются вершинами преувеличения (рис.1.8). Отрезки А1А2 = 2аиВ1В2 = 2b именуют настоящей и мнимой осями преувеличения. Прямые 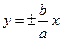 (1.48) — наклонные асимптоты преувеличения.
(1.48) — наклонные асимптоты преувеличения.
(Прямая именуется наклонной асимптотой кривой, в случае, если расстояние между точкой и этой прямой М(х, у) кривой пытается к нулю при рвении хк ± ¥ (х ® ± ¥)).
Величину 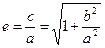 (1.49) именуют эксцентриситетом преувеличения. Разумеется, что 1 ? е ¥; при b = 0 (е = 1) преувеличение вырождается в две полупрямые, лежащие на оси Охи поделённые промежутком (–а,а).
(1.49) именуют эксцентриситетом преувеличения. Разумеется, что 1 ? е ¥; при b = 0 (е = 1) преувеличение вырождается в две полупрямые, лежащие на оси Охи поделённые промежутком (–а,а).
Фокальные радиусы – векторы определяются соотношениями:
| Левая ветвь преувеличения | Правая ветвь преувеличения | |||
| r1 = – ex + a | Правый | r1 = ex – a | Правый | (1.50) |
| r2 = – ex – a | Левый | r2 = ex + a | Левый |
При а = b (e = ) (такая преувеличение именуется равнобочной) асимптоты преувеличения – биссектрисы координатных углов.
| y |
Две преувеличения 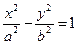 и
и 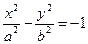 , имеющие одинаковые асимптоты и оси (мнимая ось одной сходится с настоящей осью второй) именуют сопряженными.
, имеющие одинаковые асимптоты и оси (мнимая ось одной сходится с настоящей осью второй) именуют сопряженными.
Парабола. Параболой именуется геометрическое место точек, равноудаленных от данной точки, именуемой фокусом, и данной прямой, именуемой директрисой.
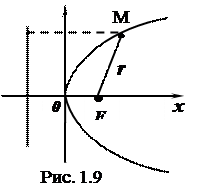
В случае, если фокус параболы в точке F(р/2, 0), а уравнение директрисы х = –р / 2, то уравнение параболы примет вид у2 = 2рх (1.51).
Эта парабола симметрична относительно оси Ох и при р 0расположена как на рис. (1.9). х2 = 2ру(1.51`) уравнение параболы, симметричной относительно оси Оу. Фокальный радиус – вектор параболы (1.51) определяется соотношением:
r = x + (p / 2) (p 0) (1.52).
Тесты
1. Какое из уравнений обрисовывает кривую второго порядка:
1) х + у + 7 = 0; 3) х2у + 7 = 0;
2) х2 + у + 7 = 0; 4) ху + + 7 = 0.
2. Уравнение х2 – 2х + у2 + 6у = 0 обрисовывает:
1) Окружность;
2) Эллипс;
3) Преувеличение;
4) Две пересекающихся прямые.
3. Эллипс задан уравнением 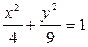 и его эксцентриситет равен:
и его эксцентриситет равен:
1) ; 2) — ; 3) ; 4) — .
4. Уравнение преувеличения 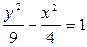 , координаты ее фокусов:
, координаты ее фокусов:
1) и ;
2) и ;
3) и ;
4) и .
5. Дана парабола у2= -8х. Уравнение ее директрисы имеет форму:
1) х = -4; 2) х = 4; 3) у = -4; 4) у = 4.