РАСЧЕТ ТРЕХФАЗНОЙ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
методические указания и Контрольные задания
к независимой работе
по направлениям «Базы теории цепей»,
«Неспециализированная электротехника»,
«Теоретические базы электротехники»
Издательство
Пермского национального технического университета
Введение
Для распределения и передачи электричества как правило употребляется трехфазная совокупность энергоснабжения, т.е. совокупность, в которой действуют три однообразные по амплитуде синусоидальные ЭДС одной и той же частоты, создаваемые одним источником энергии и перемещённые относительно друг друга по фазе на . Такая совокупность была изобретена в 1891 г. выдающимся русским инженерном М.О. Доливо-Добровольским, создавшим все ее практические приложения, включая трехфазный асинхронный двигатель и трансформатор.
В трехфазной совокупности технико-экономические преимущества синусоидальных токов проявляются в громаднейшей степени (понижается расход проводниковых материалов в линии электропередач, возрастает КПД устройств и т.п.). Исходя из этого современные энергетические совокупности делают как трехфазные совокупности генераторов, трансформаторов и линий электропередач, снабжающих трехфазным электропитанием промышленные потребители, каковые, по большей части, являются трехфазными, к примеру: асинхронные и синхронные двигатели, замечательные электрические печи, электромагниты и т.п. Однофазные потребители кроме этого приобретают питание от трехфазных сетей.
Для действенной эксплуатации таких сетей нужно знать их ограничения и возможности, существующие при подключении к ним потребителей.
Цель независимой работы студентов по данной теме – изучение фундаментальных особенностей трехфазных закономерностей и цепей распределения линейных и фазных токов и напряжений, изучение схем подключения трехфазных и однофазных потребителей к трехфазной системе электроснабжения в рабочих и аварийных режимах.
ОСНОВНЫЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Трехфазные цепи являются одним из видов цепей синусоидального тока, и, следовательно, для них полностью применимы способы анализа и расчёта цепей в символической форме. Анализ трехфазных цепей комфортно осуществлять с применением векторных диаграмм, разрешающих достаточно фазовые сдвиги между напряжениями и токами. Но существующая определенная специфика трехфазных цепей вносит характерные изюминки в их расчет.
Главным показателем классификации трехфазных совокупностей ЭДС, напряжений и токов есть их симметричность.
Симметричные трехфазные совокупности
Условиями симметричности есть равенство мгновенных (комплексных) значений ЭДС фаз генератора. Мгновенные и комплексные значения ЭДС трехфазного симметричного генератора имеют вид:
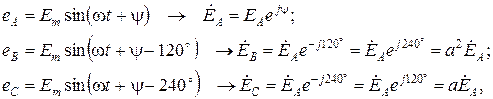(1)
где a – оператор поворота, причем
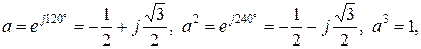и т.д.
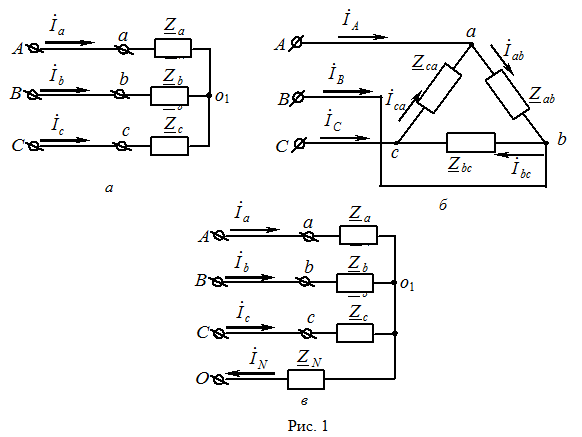
Условием симметричности трехфазного приемника есть равенство комплексных сопротивлений соответствующих фаз: т.е. в случае, если (фазы нагрузки соединены звездой, рис. 1, а) либо (фазы нагрузки соединены треугольником, см. рис. 1, б). В другом случае приемник есть несимметричным.
Существуют трехфазные совокупности, в которых нулевые точки генератора О и нагрузки о1 соединяются проводом с сопротивлением либо (см. рис. 1, в). Таковой провод именуют нулевым либо нейтральным проводом.
В случае, если к симметричной трехфазной цепи приложена симметричная трехфазная совокупность напряжений генератора, то в ней будет функционировать симметричная совокупность токов. Таковой режим работы трехфазной цепи именуется симметричным. В этом режиме напряжения и токи соответствующих фаз равны по модулю и перемещены по фазе на . Расчет таких цепей проводится для одной (базисной) фазы, в качестве которой в большинстве случаев принимают фазу А. Наряду с этим соответствующие размеры в других фазах приобретают формальным добавлением к доводу переменной фазы А фазового сдвига при сохранении неизменным ее модуля.
Для симметричной трехфазной совокупности при соединении нагрузки звездой (см. рис. 1, а) существуют следующие зависимости между действующими значениями линейных и фазных напряжений и токов:
, (2)
между комплексными значениями токов фаз
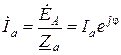; ; . (3)
При наличии нейтрального провода ток в этом проводе определяется по первому закону Кирхгофа
, (4)
при отсутствии нейтрального провода
. (5)
Для симметричной трехфазной совокупности при соединении нагрузки треугольником (см. рис. 1, б) действующие значения линейных и фазных напряжений и токов связаны соотношениями:
, (6)
комплексные значения токов фаз
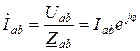; ; , (7)
комплексные значения линейных токов
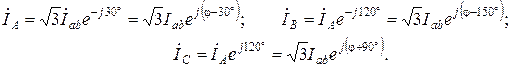(8)
Комплексная, полная, активная и реактивная мощности в симметричной трехфазной совокупности определяются соответственно по нижеуказанным формулам
для схем «звезда – звезда»
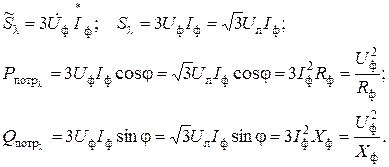(9)
для схем «треугольник – треугольник»
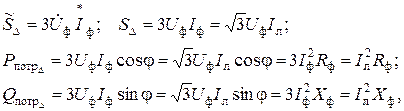(10)