ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ СПОСОБОМ КОНЕЧНЫХ РАЗНОСТЕЙ
Цель работы
Ознакомление с способами ответа смешанных задач для дифференциальных уравнений параболического типа, с понятием устойчивости численных способов, и со методами разработки экономных программ и алгоритмов. Работу можно считать расчетно-графической в связи с возможностью наглядного графического представления функции двух переменных.
Описание способа
Разглядим стержень из теплопроводящего материала с коэффициентом теплопроводности k. Предположим, что температура на финишах стержня задана, а боковая поверхность стержня теплоизолирована. Пускай ось x направлена на протяжении оси стержня, а его финиши находятся в точках x=0 и x=L. Тогда задача сводится к определению зависимости от времени температуры u в точках стержня, другими словами функции двух переменных u(x,t). Функция u(x,t) обязана удовлетворять уравнению теплопроводности
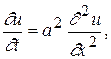(0
начальному условию
u(x,0)=f(x), (0
и условиям на финишах стержня
u(0,t)=j1(t), u(L,t)=j2(t), (tV0). (3)
Значения u(0,0) и u(L,0), полученные из (2) и (3), должны совпадать. Это будет в случае, если j1(0)=f(0), j2(0)=f(L).
направляться подчернуть, что методом замены переменных t^=a2t уравнение (1) возможно преобразовать к виду
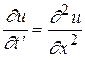. (4)
Это указывает, что ответ задачи (1)-(3) методом замены переменных сводится к ответу задачи (4),(2),(3). Потом будем полагать а=1.
Выстроим на плоскости (x,t) сетку с шагом h по переменной x (xi = (i-1)h, i=1,..,n+1, h=L/n) и с шагом t по переменной t (tj = (j-1)t). Обозначим uij = u(xi,tj). Производные в уравнении (1) аппроксимируем следующим образом:
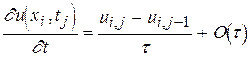, (5)
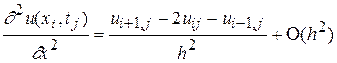. (6)
Подставляя (5) и (6) в (1) при a=1, возьмём разностное уравнение:
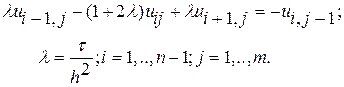(7)
В соответствии с (2) и (3) значения
ui0 = f(xi), u0j = j1(tj), unj = j2(tj) (8)
являются известными. Тогда, подставляя в (7) j=0, возьмём совокупность n-1 линейных уравнений, решив которую возможно выяснить ui1, i=1,..,n-1. Наряду с этим, потому, что u01=j1(t1), un1=j2(t1), известными оказываются все значения временного слоя j=1, (t=t1). После этого, подставляя в (7) j=2, решаем совокупность уравнений довольно ui2 и т.д. для всех j=2,..,m.
Из (7) направляться, что в каждое i-тое уравнение (i=1,..,n-1) с ненулевыми коэффициентами входят лишь три малоизвестных ui-1,j; uij; ui+1,j. Величина ui,j-1 сейчас есть известной и потому отнесена в правую часть уравнения. Так, матрица совокупности уравнений есть трехдиагональной и эту совокупность возможно решить способом прогонки. Для этого представим ее в стандартном виде:
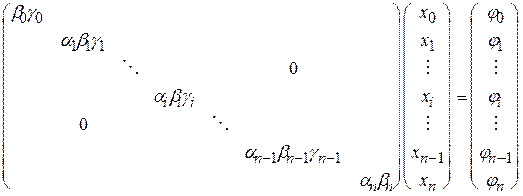.(9)
Для данной задачи xi=uij, ai = l, gi = l, bi = 1-2l, b0 = 1, g0 = 0, j0 = u0j = j1(tj), jn = unj = j2(tj), ji = -ui,j-1 (i=1,..,n-1).
Пускай на j-том шаге заданными являются параметры ui,j-1 (i=1,..,n-1), u0j, unj, l. Все малоизвестные значения uij возможно разместить в массиве xi (xi=uij, i=0,..,n). Ищем сообщение xi-1 с xi в виде рекуррентного соотношения
xi-1=ci-1xi+ni-1, i=1,..,n. (10)
Подставляя (10) в (7), приобретаем
lci-1xi-(1+2l)xi+lxi+1 = -ui,j-1-lni-1.
Из этого
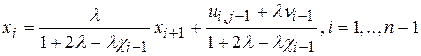(11)
Сравнивая (11) с (10), находим рекуррентные соотношения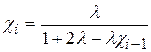 
,
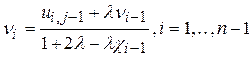, (12)
c0= 0, n0 = u0j .
Так, метод определения значений uij по известным ui,j-1 складывается из двух этапов: прямого хода прогонки по формулам (12) при i=1,..,n-1 и обратного хода прогонки по формуле (10) при i=n,..,2.
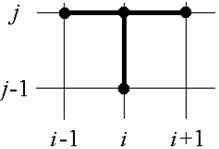 а) |
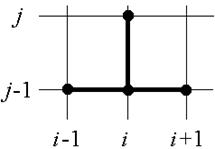 б) |
Рис. 5.1
Нужно подчернуть, что разностное уравнение (7) связывает одно известное значение Ui,j-1 (из прошлого j-1 временного слоя) и три малоизвестных Ui,j, Ui-1,j, Ui+1,j. Исходя из этого определить значения Ui,j (i=1,…,n-1) возможно лишь все сходу методом решения совокупности уравнений. Такая схема связи переменных в разностном уравнении именуется неявной. Шаблон неявной разностной схемы представлен на рис. 5.1а.
Наровне с неявной вероятна организация явной разностной схемы. Для этого вместо выражения (5) для первой разностной производной по времени применяют формулу
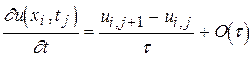, (13)
Тогда разностное уравнение запишется в виде
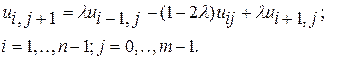(14)
В этом случае связываются три малоизвестные значения, относящиеся к прошлому временному слою (тут j-тому) и лишь одно малоизвестное Ui,j+1. Шаблон явной разностной схемы представлен на рис. 5.1а.
При применении данной схемы малоизвестные параметры определяются методом последовательного применения формулы (2.14) при i=1,…n-1. Потому, что наряду с этим не нужно решать совокупности уравнений, то процесс определения параметров одного временного слоя требует меньших затрат времени, чем при неявной схемы.
Но, неявная схема устойчива (неточность не возрастает от шага к шагу) при любых значениях l=t/h2. Явная схема есть устойчивой лишь при l
При применения неявной схемы затраты машинного времени для расчета одного временного слоя больше, но возможность выбора намного большего шага по времени t может обеспечить неспециализированное ускорение процесса расчета если сравнивать с явной схемой.
При исполнении данной работы будем предполагать, что температура на финишах стержня поддерживается постоянной, другими словами
j1(t)Tf(0), j2(t)Tf(L).