К таким уравнениям относятся уравнения вида
.
Методом алгебраических преобразований данное уравнение приводят к уравнениям вида , именуемым уравнениями с поделёнными переменными. Функции , вычисляют постоянными.
По окончании интегрирования уравнения находим неспециализированное ответ дифференциального уравнения либо неспециализированный интеграл: . Тут – неспециализированное ответ.
Ответ однородных дифференциальных уравнений первого порядка
Уравнение именуется однородным, в случае, если P и Q однородные функции от x и y однообразного измерения.
Однородные уравнения приводятся к виду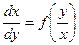 
и решаются подстановкой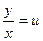 
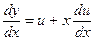как уравнения с разделяющимися переменными.
Ответ дифференциальных уравнений второго порядка, допускающих понижение порядка
1) Уравнение вида решается последовательным n-интегрированием правой части. При каждом интегрировании получается одно произвольное постоянное, а в окончательном результате – n произвольных постоянных.
2) Уравнение , не содержащее y в явной форме, приводиться подстановкой ,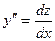 
к уравнению первого порядка 
.
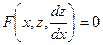3) Уравнение , не содержащее x в явной форме, подстановкой ,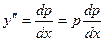 
приводиться к уравнению первого порядка 
.
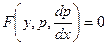Ответ линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
Уравнение , в котором коэффициенты постоянны, возможно привести к уравнению вида
Частное ответ для того чтобы уравнения ищется в виде функции . Два раза дифференцируя эту функцию и подставляя выражения , , , возьмём уравнение . Так как , то, уменьшая на , возьмём уравнение .
Алгебраическое уравнение для определения коэффициента k именуется характеристическим уравнением данного дифференциального уравнения.
Характеристическое уравнение есть уравнением второй степени и имеет два корня. Эти корни смогут быть либо настоящими разными, либо настоящими и равными, либо комплексными сопряженными.
Приведем таблицу формул неспециализированного ответа уравнения в зависимости от вида корней характеристического уравнения:
| Уравнение | |||
| Характеристическое уравнение | |||
| Корни характеристического уравнения | |||
| Фундаментальная совокупность частных ответов | |||
| Формула неспециализированного ответа |
Ответ типовых задач
1) Выяснить тип дифференциального уравнения и отыскать его неспециализированное ответ
xydx + (x + 1)dy = 0.
Ответ:
Задано дифференциальное уравнение первого порядка с разделяющимися переменными.
Поделим переменные:(x + 1)dy = – xydx;
;
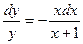проинтегрируем уравнение: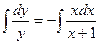 
;
;
.
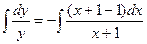
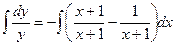
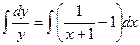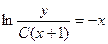
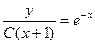Так, – неспециализированное ответ дифференциального уравнения.
2) Выяснить тип дифференциального уравнения и отыскать его неспециализированное ответ
.
Ответ:
Задано однородное дифференциальное уравнение первого порядка.
Приведем его к виду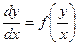 
:
.
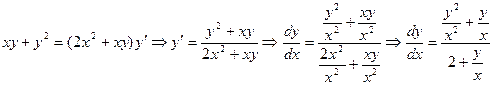Подстановкой , ,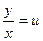 
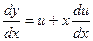приведем данное уравнение к уравнению с разделяющимися переменными: 
.
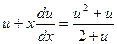Поделим переменные: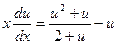 
.
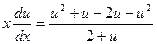
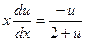
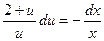Проинтегрируем последнее уравнение:
;
.
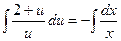
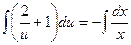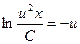
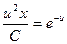Выполним обратную подстановку: так как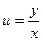 
, то приобретаем:
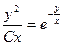либо – неспециализированный интеграл заданного дифференциального уравнения.
3) Выяснить тип дифференциального уравнения и отыскать его неспециализированное ответ
.
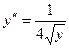Ответ:
Задано дифференциальное уравнение второго порядка, допускающее понижение порядка и не содержащее х в явном виде.
Понизим порядок данного уравнения подстановкой ,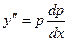 
:
.
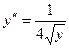
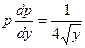Поделим переменные: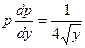 
.
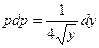Проинтегрируем последнее уравнение:
.
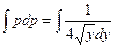
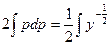Так как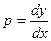 
, то приобретаем дифференциальное уравнение первого порядка с разделяющимися переменными: 
.
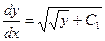Поделим переменные и проинтегрируем:
;
.
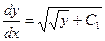
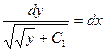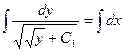Отыщем левый интеграл, применяя способ замены переменной:
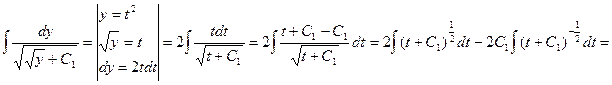
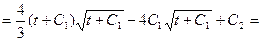(т. к. , исходя из этого приобретаем) 
.
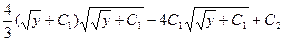Совсем находим:
.
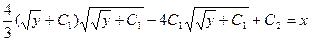Так, 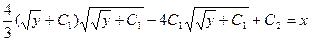– неспециализированное ответ дифференциального уравнения.
4) Выяснить тип дифференциального уравнения и отыскать его частное ответ
, , .
Ответ:
Задано линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами.
Составим и решим характеристическое уравнение:
.
По теореме Виета находим корни: , другими словами корни настоящие и разные. Из таблицы формул неспециализированного ответа находим, что , имеется неспециализированное ответ заданного дифференциального уравнения.
Значения постоянных отыщем из начальных условий:
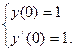
Вычисляем производную и приобретаем совокупность линейных уравнений:
.
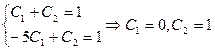Запишем частное ответ: .
Так, – частное ответ дифференциального уравнения , удовлетворяющее начальным условиям .
Упражнения
Задание 1. Отыскать неспециализированное ответ дифференциального уравнения первого порядка с разделяющимися переменными:
1.
2.
3.
4.
5. 
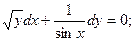
6.
7.
8. ;
9. ;
10. ;
11. ;
12. ;
13. ;
14.
Задание 2. Отыскать общее и частное ответа дифференциального уравнения первого порядка с разделяющимися переменными:
1. , при x=0, y=0;
2. 
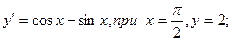
3.
4.
5. 
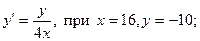
6. 
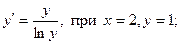
7.
8. 
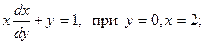
Задание 3. Отыскать неспециализированное ответ и, где указано, частное ответ линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами:
1.
2.
3.
4.
5. ;
6. ;
7. 
;
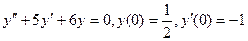8. ;
9. ;
10.
Базы теории возможностей
Теория возможностей – раздел математики, где изучаются закономерности случайных событий.
Теория возможностей обязана давать количественное измерение возможностей случайных явлений и построение на данной базе математической модели замечаемых случайных эмпирических соотношений.
событие и Испытание
В повседневной жизни и природе довольно часто приходится сталкиваться случайными явлениями, т. е. с обстановками, финал которых запрещено совершенно верно предвидеть. Процесс познания действительности в этом случае осуществляется в следствии наблюдений либо опробований (опытов).
Под опробованием (наблюдением) понимается любой дешёвый нередкому повторению процесс, протекающий при реализации заданного комплекса условий.
Итог, либо финал опробования именуется событием.
Виды событий
Различают три вида событий: случайные, точные и неосуществимые.
Событие, которое при реализации заданного комплекса условий может случиться, быть может и не случиться, именуется случайным.
Событие, которое неизбежно происходит при каждой реализации заданного комплекса условий, именуется точным.
Событие, которое заведомо не имеет возможности случиться при реализации заданного комплекса условий, именуется неосуществимым.
Виды случайных событий
Случайные события подразделяются на следующие виды: равновозможные, несовместные и совместные.
Два либо пара случайных событий именуются равновозможными, в случае, если условия их появления однообразны и нет основания утверждать, что какое-либо из них в следствии опробования имеет больше шансов осуществиться, чем другие.
События именуются несовместными, в случае, если в следствии опробования осуществление одного из них исключает осуществление остальных.
Два события именуются совместными, в случае, если появление одного из них не исключает появления другого в одном и том же опробовании.
Полная несколько событий
В случае, если в следствии опробования непременно осуществится одно и лишь одно из несовместных событий , то эти события именуются полной группой событий.
Два несовместных события, образующие полную группу событий, именуются противоположными.
Финалы опробования
Несовместные события, имеющие однообразную возможность осуществиться, именуются финалами опробования.
Финалы именуются благоприятными для события , в случае, если осуществление любого из финалов есть вместе с тем осуществлением события .
Операции над событиями
Определение. В случае, если при каждом осуществлении заданного комплекса условий, при котором происходит событие , происходит и событие , то говорят, что влечёт за собой , и обозначают знаком либо .
В случае, если влечет за собой и одновременно с этим влечёт за собой , т.е. события и оба наступают либо оба не наступают, то говорят, что события и равносильны, и обозначают знаком .
Событие, пребывающее в наступлении обоих событий и , именуется произведением (либо пересечением) событий и , и обозначается знаком либо .
Событие, пребывающее в наступлении хотя бы одного из событий и , (быть может, двух сходу), именуется суммой (либо объединением) событий и , и обозначается знаком либо
Событие, пребывающее в том, что событие происходит, а событие не происходит, именуется разностью событий и , и обозначается знаком либо .
Точное событие обозначают посредством знака , а неосуществимое – посредством знака .
Событие, противоположное событию , обозначают посредством знака .
произведения и Определение суммы двух событий обобщается на любое число событий.
Понятие возможности