Дифференциальные уравнения
1.1. Дифференциальные уравнения первого порядка. Главные определения.
Дифференциальным уравнением именуется уравнение, связывающее свободную переменную x, малоизвестную ее производные и функцию либо дифференциалы.
Замечание: Необходимым в дифференциальном уравнении есть лишь наличие производных либо дифференциалов.
Порядком дифференциального уравнения именуется порядок высшей производной, в него входящей.
В случае, если дифференциальное уравнение зависит лишь от одной переменной, то оно именуется обычным дифференциальным уравнением.
Обычное дифференциальное уравнение первого порядка имеет форму:
.(1.1.1)
В случае, если уравнение (1.1.1) дать добро относительно производной, то его возможно записать в виде:
. (1.1.2)
Решениемуравнения (1.1.2) есть дифференцируемая функция , которая при подстановке в уравнение (1.1.2) обращает его в тождество. График ответа дифференциального уравнения именуется интегральной кривой.
Геометрический суть дифференциального уравнения первого порядка:
Уравнение устанавливает связь между координатами точек интегральных кривых (правая часть уравнения) и угловым коэффициентом касательной (левая часть уравнения) к интегральным кривым в этих точках, т.е. уравнение определяет поле направленийинтегральных кривых.
Уравнение (1.1.2) определяет целое семейство ответов. Дабы выделить одно ответ, задают начальное условие:
, (1.1.3)
где – начальное значение довода , а – начальное значение функции.
Задача Кошизаключается в отыскании функции , удовлетворяющей уравнению (1.1.2) и начальному условию (1.1.3).
Неспециализированным решениемдифференциального уравнения (1.1.2) именуется ответ этого уравнения, которое:
1) зависит от произвольной постоянной с;
2) для всякого начального условия (1.1.3) возможно отыскать такое значение постоянной , что функция будет удовлетворять данному начальному условию.
Ответ именуется частным решениемуравнения (1.1.2), соответствующим начальным условиям (1.1.3).
Уравнение с разделяющимися переменными
Разглядим уравнение вида:
, (1.2.1)
где функция зависит лишь от , а функция лишь от . Преобразуем его так:
;
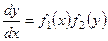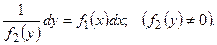
Полагая известной функцией от , возможно разглядывать последнее равенство, как равенство двух дифференциалов, а неизвестные интегралы от них будут различаться лишь постоянным слагаемым. Интегрируя левую часть по , а правую – по , отыщем:
.
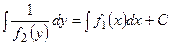т.е. возьмём неспециализированный интеграл уравнения (1).
Уравнение вида
(1.2.2)
именуется уравнением с поделёнными переменными.
Неспециализированный интеграл уравнения (1.2.2):
.
Уравнение с разделяющимися переменными возможно задано в виде:
.
Дабы поделить переменные, нужно обе части уравнения поделить на выражение :
;
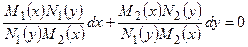либо:
,
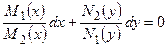т.е. к уравнению вида (1.2.2).
Однородное уравнение
Определение 1.Функция именуется однородной функцией n-го измерения довольно переменных и , в случае, если при любом справедливо тождество:
.
Пример: ; , т.е. — однородная функция первого измерения.
Определение 2.Уравнение именуется однородным довольно и , в случае, если:
а) функция — имеется однородная функция нулевого измерения довольно и ;
б) его возможно представить в виде:
, (1.3.1)
где правая часть зависит лишь от отношения ;
в) либо:
,
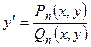где и — однородные функции однообразного порядка.
Пример: =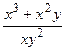 
;
а)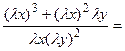 
= ;
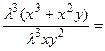
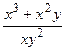т.е. — функция нулевого измерения довольно и , следовательно, дифференциальное уравнение есть однородным.
б)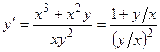 
— правая часть зависит лишь от отношения ;
в) 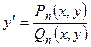= 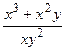— в знаменатель и числитель стоят однородные функции однообразного измерения ( ).
Подстановка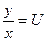 
, где приводит однородное уравнение (1.3.1) к уравнению с разделяющимися переменными. Из этого:
, ;
;
;
;
.
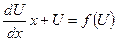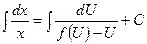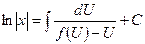Отыскав интеграл в правой части и подставив вместо функции отношение , возьмём интеграл уравнения.
Однородное уравнение довольно часто задается в дифференциальной форме:
,
где и — однородные функции однообразного порядка (измерения).
В этом случае подстановка ; сходу преобразует уравнение в уравнение с разделяющимися переменными.
Ответ: Способ Бернулли.
Будем искать ответ уравнения (1.4.1) в виде произведения двух функций от :
. (1.4.2)
Одну из функций возможно забрать произвольной, вторая определяется на основании уравнения (1.4.1). Продифференцируем (1.4.2):
,
подставим в (1.4.1):
,
либо:
Подберем функцию так, дабы выполнялось условие:
. (1.4.3)
Из исполнения этого условия направляться, что
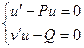(1.4.5)
Уравнение (1.4.3) – уравнение с разделяющимися переменными. Проинтегрировав его, возьмём какое-нибудь частное ответ :
.
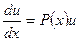
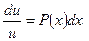
Так как достаточно какого-нибудь хорошего от нуля ответа уравнения (1.4.3), то за функцию заберём
(1.4.6)
и подставим во второе уравнение совокупности:
,
,
,
.
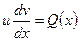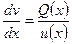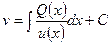Подставляя полученные значения и в формулу (1.4.2), возьмём:
,
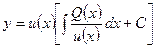либо:
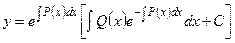. (1.4.7)
Уравнение Бернулли
Уравнение вида:
, (1.5.1)
где и — заданные постоянные функции от , а – любое настоящее число.
При уравнение преобразовывается в линейное, а при – в уравнение с разделяющимися переменными.
При помощи подстановки
, , из этого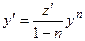 
,
где z – новая малоизвестная функция, уравнение Бернулли преобразовывается в линейное уравнение довольно z:
.
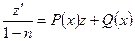Но на практике при интегрировании нет необходимости преобразовывать это уравнение в линейное. Тут возможно воспользоваться способом Бернулли, т.е. ответ искать виде произведения двух функций:
.
Необходимость
Допустим, что
,
тогда, зная формулу дифференциала
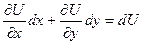
возьмём равенства:
, 
.
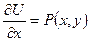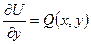Из этого можно отыскать
, 
.
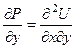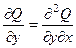Применяя теорему о независимости смешанных производных от порядка вычисления, возьмём:
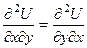, либо 
.
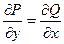Достаточность
Пускай в некоей области выполняется условие:
.
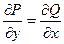Будем искать функцию следующим образом: из условия
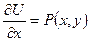
отыщем
, (1.6.2)
где — произвольная функция лишь одного довода. Выберем функцию так, дабы выполнялось еще одно условие:
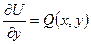. (1.6.3)
Продифференцируем обе части равенства (1.6.2) по :
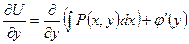, (1.6.4)
Тогда, сравнивая равенства (1.6.3) и (1.6.4), возьмём:
,
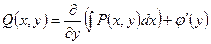откуда
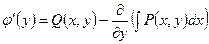. (1.6.5)
Левая часть равенства (1.6.5) зависит лишь от y и не содержит x, исходя из этого имеет суть лишь в том случае, в то время, когда правая часть равенства не содержит x. Продифференцируем правую часть по x и убедимся, что производная равна нулю. Вправду,
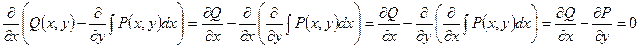
в силу условия:
.
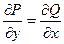Интегрируя равенство (1.6.5) по y, находим и подставляем определённое значение в равенство (1.6.2).
Неспециализированное ответ уравнения (6.1) имеет форму:
Определение 3
Два уравнения и решения (2.2.1) именуются линейно-свободными на отрезке , в случае, если их отношение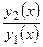 
не есть постоянным на этом отрезке. В другом случае функции именуются линейно-зависимыми на отрезке .
Дифференциальные уравнения
1.1. Дифференциальные уравнения первого порядка. Главные определения.
Дифференциальным уравнением именуется уравнение, связывающее свободную переменную x, малоизвестную ее производные и функцию либо дифференциалы.
Замечание: Необходимым в дифференциальном уравнении есть лишь наличие производных либо дифференциалов.
Порядком дифференциального уравнения именуется порядок высшей производной, в него входящей.
В случае, если дифференциальное уравнение зависит лишь от одной переменной, то оно именуется обычным дифференциальным уравнением.
Обычное дифференциальное уравнение первого порядка имеет форму:
.(1.1.1)
В случае, если уравнение (1.1.1) дать добро относительно производной, то его возможно записать в виде:
. (1.1.2)
Решениемуравнения (1.1.2) есть дифференцируемая функция , которая при подстановке в уравнение (1.1.2) обращает его в тождество. График ответа дифференциального уравнения именуется интегральной кривой.
Геометрический суть дифференциального уравнения первого порядка:
Уравнение устанавливает связь между координатами точек интегральных кривых (правая часть уравнения) и угловым коэффициентом касательной (левая часть уравнения) к интегральным кривым в этих точках, т.е. уравнение определяет поле направленийинтегральных кривых.
Уравнение (1.1.2) определяет целое семейство ответов. Дабы выделить одно ответ, задают начальное условие:
, (1.1.3)
где – начальное значение довода , а – начальное значение функции.
Задача Кошизаключается в отыскании функции , удовлетворяющей уравнению (1.1.2) и начальному условию (1.1.3).
Неспециализированным решениемдифференциального уравнения (1.1.2) именуется ответ этого уравнения, которое:
1) зависит от произвольной постоянной с;
2) для всякого начального условия (1.1.3) возможно отыскать такое значение постоянной , что функция будет удовлетворять данному начальному условию.
Ответ именуется частным решениемуравнения (1.1.2), соответствующим начальным условиям (1.1.3).
Уравнение с разделяющимися переменными
Разглядим уравнение вида:
, (1.2.1)
где функция зависит лишь от , а функция лишь от . Преобразуем его так:
;
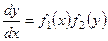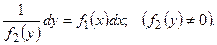
Полагая известной функцией от , возможно разглядывать последнее равенство, как равенство двух дифференциалов, а неизвестные интегралы от них будут различаться лишь постоянным слагаемым. Интегрируя левую часть по , а правую – по , отыщем:
.
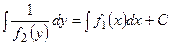т.е. возьмём неспециализированный интеграл уравнения (1).
Уравнение вида
(1.2.2)
именуется уравнением с поделёнными переменными.
Неспециализированный интеграл уравнения (1.2.2):
.
Уравнение с разделяющимися переменными возможно задано в виде:
.
Дабы поделить переменные, нужно обе части уравнения поделить на выражение :
;
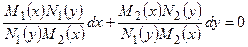либо:
,
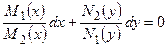т.е. к уравнению вида (1.2.2).
Однородное уравнение
Определение 1.Функция именуется однородной функцией n-го измерения довольно переменных и , в случае, если при любом справедливо тождество:
.
Пример: ; , т.е. — однородная функция первого измерения.
Определение 2.Уравнение именуется однородным довольно и , в случае, если:
а) функция — имеется однородная функция нулевого измерения довольно и ;
б) его возможно представить в виде:
, (1.3.1)
где правая часть зависит лишь от отношения ;
в) либо:
,
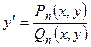где и — однородные функции однообразного порядка.
Пример: = ;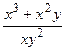
а) = ;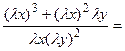
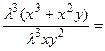
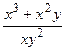т.е. — функция нулевого измерения довольно и , следовательно, дифференциальное уравнение есть однородным.
б) 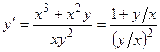— правая часть зависит лишь от отношения ;
в) 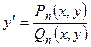= 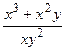— в знаменатель и числитель стоят однородные функции однообразного измерения ( ).
Подстановка 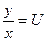, где приводит однородное уравнение (1.3.1) к уравнению с разделяющимися переменными. Из этого:
, ;
;
;
;
.
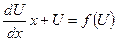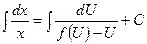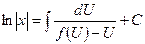Отыскав интеграл в правой части и подставив вместо функции отношение , возьмём интеграл уравнения.
Однородное уравнение довольно часто задается в дифференциальной форме:
,
где и — однородные функции однообразного порядка (измерения).
В этом случае подстановка ; сходу преобразует уравнение в уравнение с разделяющимися переменными.