ЛЕКЦИЯ №16
НЕСПЕЦИАЛИЗИРОВАННЫЕ ПОНЯТИЯ О РАЗВЁРТЫВАНИИ ПОВЕРХНОСТЕЙ.
КОНИЧЕСКОЙ ПОВЕРХНОСТИ и РАЗВЁРТКИ ПИРАМИДЫ.
НЕСПЕЦИАЛИЗИРОВАННЫЕ ПОНЯТИЯ О РАЗВЁРТЫВАНИИ ПОВЕРХНОСТЕЙ
Будем разглядывать поверхность как эластичную нерастяжимую оболочку. В этом случае кое-какие поверхности путём преобразования возможно совместить с плоскостью без складок и разрывов. Поверхности, допускающие такое преобразование, именуются развёртывающимися.
Фигура, получающаяся при совмещении развертывающейся поверхности с плоскостью, именуется разверткой.
Построение развёрток имеет громадное значение при конструировании изделий из листового материала (сосуды, трубопроводы, выкройки и т.д.).
Поверхности, развертывающиеся геометрически совершенно верно: многогранные, конические, торсы, цилиндрические.
Из кривых поверхностей, к числу развёртывающихся относятся те линейчатые поверхности (конические, цилиндрические, торсы), у которых касательная плоскость касается поверхности по её прямолинейной образующей.
Все остальные кривые поверхности относятся к числу не развертывающихся, но при необходимости возможно выстроить их приближённыеразвёртки.
Для построения развёртки какой-либо криволинейной поверхности её разбивают на такие криволинейные участки, любой из которых возможно аппроксимировать некоей плоской фигурой, которая требует для определения собственной натуры лишь замеров.
К примеру:
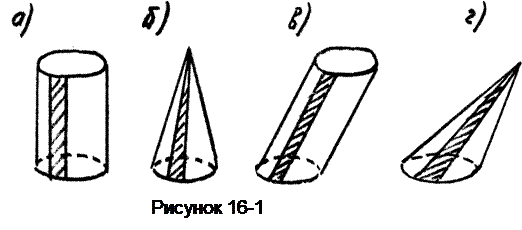
- цилиндр разбивают на прямоугольники (рисунок 16-1а);
- прямой конус на равнобедренные треугольники (рисунок 16-1б);
- эллиптический цилиндр — на параллелограммы (рисунок 16-1в);
- эллиптический конус — на треугольники (рисунок 16-1г);
- сферу — на трапеции.
 |
КОНИЧЕСКОЙ ПОВЕРХНОСТИ и РАЗВЁРТКИ ПИРАМИДЫ
В качестве примеров разглядим построение разверток лишь четырех поверхностей: пирамиды, конуса, цилиндра и призмы.
Развертка поверхности пирамиды
Развёртка таковой поверхности представляет собой плоскую фигуру, которая получается совмещением всех её граней с одной плоскостью.
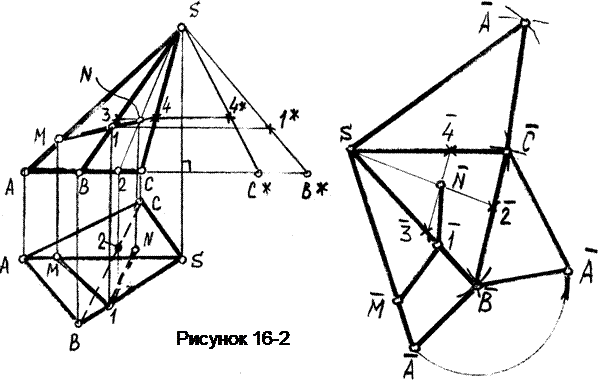
Пример 1. Выстроить развёртку поверхности пирамиды АВСS (рисунок 16-2) и нанести на неё линиюМN.
Так как боковыми гранями пирамиды являются треугольники, то для построения развёртки нужно отыскать натуральный вид этих треугольников, для чего направляться выяснить подлинные длины сторон — ребер пирамиды.
Основание пирамиды лежит в горизонтальной плоскости, следовательно, натуральная величина ребер АВ, ВС и АС уже имеется на чертеже.
Ребро SA есть фронталью, исходя из этого на виде спереди оно изображается в натуральную величину.
Натуру ребер SВ и SС определяем методом прямоугольного треугольника. Одним катетом его есть превышение точки S над точками В и С, а вторым — вид сверху ребер SВ и SС.
После этого по трём сторонам строим последовательно все боковые грани пирамиды.
Для нанесения на развёртку линии МN сначала определим подлинную величину отрезков AM и В1 и отложим их на развёртке на соответствующих ребрах.
Дабы нанести точку М, совершим на грани SВС прямую S2 и отыщем её положение на развёртке, отложив отрезок В2 (замеренный на виде сверху) на стороне ВC. После этого на виде спереди совершим через точку 4 отрезок 3-4, параллельный ребру ВС и отыщем его положение на развёртке, для чего отложим отрезок C4 на стороне SС и через взятую точку совершим прямую 3-4 параллельную ребру ВС. На пересечении прямых S-2 и 3-4 отыщем точку N. Соединив полученные точки М, 1, N возьмём искомую линию.
Развертка конической поверхности
Для построения развёртки конической поверхности нужно вписать в неё (либо обрисовать около неё) многогранную поверхность, т.е. заменить поверхность вращения многогранной поверхностью.
В этом случае поверхность разбивается на треугольники, и таковой метод построения развёрток именуется методом треугольников(метод триангуляции).
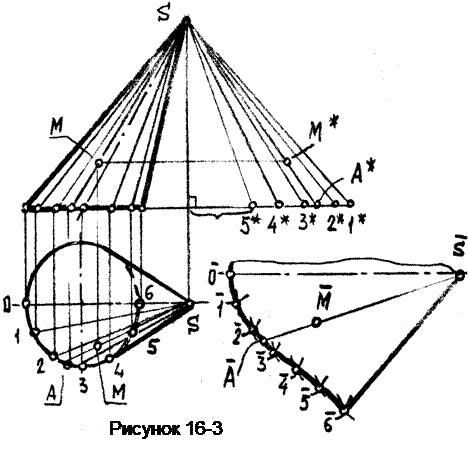
Пример 2. Выстроить развёртку боковой поверхности эллиптического конуса (рисунок 16-3) и нанести на неё точку М.
Заменим данную коническую поверхность поверхностью вписанной двенадцатиугольной пирамиды. Развёртка пирамиды будет складываться из последовательности примыкающих друг к другу треугольников. Другими словами. построение развертки конуса сводится к построению развертки пирамиды (см. выше).
Для построения натурального вида этих треугольников нужно выяснить натуральные размеры образующих конуса (совершённых в точки деления основания) методом прямоугольного треугольника.
Натура сторон треугольника, лежащих в основании конуса равна хорде стягивающей дугу окружности: 1-2 = 2-3 = 3-4 = и т.д., и на виде сверху изображается в натуральную величину. Так как развёртка представляет собой симметричную фигуру, то выстроим развёртку лишь половины поверхности конуса.
По окончании построения развёртки находим на ней положение точки М. Для этого совершим через точку М образующую конуса АS, определим её положение и натуру точки М на ней (отрезок А*М*). После этого находим положение образующей АS на развёртке, для чего замеряем на виде сверху хорду А2 и откладываем её на развёртке от точки 2 в сторону точки 3. Соединяем точку А с точкой S и на данной прямой откладываем отрезок A*М*.
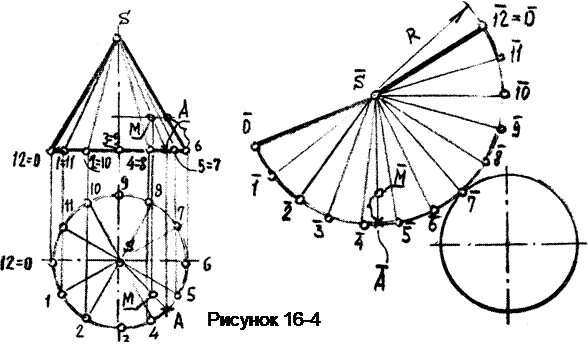
Пример З. Выстроить развёртку поверхности прямого кругового конуса и нанести на нее точку М (рисунок 16-4).
Развёртка боковой поверхности кругового конуса представляет собой круговой сектор, радиус которого равен натуральной величине образующей конуса, а протяженность дуги равна длине окружности основания конуса. Фактически длину дуги определяют длинами хорд, стягивающих дуги основания (1-2 = 2-3 = 3-4 = и т.д.), замеренными на виде сверху. Построение точки М на развёртке подобно примеру 2.
 |