Из условии? равновесия узлов либо посредством вариационных правил, и способов невязок, используемых ко всей само собой разумеется- элементной модели, составляется неспециализированная совокупность уравнении? равновесия всей конечно-элементной модели исследуемого деформируемого тела. Для статических задач она имеет форму:
где неспециализированная (глобальная) матрица жесткости конечно-элементнои? модели;
{ Р } неспециализированный вектор заданных внешних узловых сил;
неспециализированные (глобальные) векторы узловых сил, эквивалентных распределенным поверхностным и массовым силам, начальным деформациям, начальным напряжениям.
Компоненты матрицы являются коэффициентами жесткости модели. Они вычисляются методом суммирования соответствующих коэффициентов жесткости конечных элементов. Матрица жесткости для конечно-элементнои? модели владеет симметрией, имеет редкое заполнение и ленточную структуру.
Неспециализированный вектор заданных внешних узловых сил {Р} возможно пред ставить в виде:
где подматрица из n1 компонентов силы, приложенной в узле i. Для трехмерной задачи будем иметь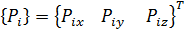 
. Как видно из выражения (6), индексация компонентов возможно либо по неспециализированным номерам степеней свободы модели либо по неспециализированным номерам узлов с добавлением индекса узловой степени свободы, как у неспециализированного вектора узловых перемещении? (2).
Неспециализированные (глобальные) векторы узловых сил планируют из компонентов соответствующих элементных векторов. Их структура такая же, как у вектора .
В динамических задачах на основании принципа Даламбера в уравнения (5) добавляются силы инерции. Так как силы инерции выражаются через ускорения, каковые являются вторыми производными от перемещении?, то уравнения равновесия (5) преобразовываются в неспециализированные (глобальные) дифференциальные уравнения перемещения, в которых внешние силы смогут быть переменными:
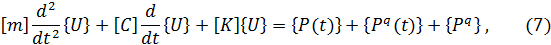
где и неспециализированные (демпфирования) модели и глобальные матрицы масс, каковые планируют из компонентов соответствующих элементных матриц.
Посредством уравнении? (7) выполняются разные виды динамического анализа: модальный анализ, где определяются формы конструкции и собственные частоты?; гармонический анализ, где определяется отклик совокупности на внешнюю периодическую силу с разной частотой; полный анализ динамического процесса, где производится интегрирование дифференциальных уравнении? перемещения.
В статических задачах задаваемые перемещения (связи) должны исключать возможность перемещения нагруженной конструкции как полностью жёсткого тела. Лишь в этом случае разрешающая совокупность уравнении? (5), по окончании учета граничных условии?, будет иметь единственное ответ. До учета связей исходная совокупность (5) имеет линейно зависимые уравнения, определитель ее матрицы жесткости равен нулю, следовательно, матрица жесткости свободного тела есть сингулярной, и нельзя найти однозначного ответа для узловых перемещении?. [5, 7] Динамические задачи, обрисовываемые уравнениями (7), смогут решаться без наложения связей — перемещении?.
Ответ уравнений МКЭ
Неспециализированная совокупность уравнении? равновесия (5), полученная способом конечных элементов для статической линейно-упругой модели тела, есть, с математической точки зрения, совокупностью линейных алгебраических уравнении? (СЛАУ). По окончании учета верно наложенных связей, не допускающих перемещения модели как полностью жёсткого тела, определитель матрицы жесткости [К] не равен нулю и, следовательно, существует единственное ответ — неспециализированный вектор узловых перемещении? {U}.
эффективность и Точность разных способов ответа СЛАУ (5) сильно зависит от свойств и структуры матрицы [К]: размера, обусловленности, симметричности, заполненности и др. [2]. Узнаваемые методы ответа СЛАУ возможно поделить по большей части на две группы: прямые итерационные методы и методы [1, 2, 5, 6].
Прямые («правильные») способы разрешают приобретать посредством конечного числа операции? правильные значения малоизвестных, в случае, если правые и коэффициенты части уравнении? заданы совершенно верно и нет округлении? при вычислениях. Среди множества прямых способов громаднейшее использование имеют: способ исключения малоизвестных Гаусса, способ квадратного корня, и их разновидности, например, схема разложения и фронтальный метод Холецкого.
Итерационные способы характеризуются тем, что сначала задаются некоторыми приближенными значениями малоизвестных. После этого посредством каких-либо методов их последовательно уточняют, приближаясь к правильному ответу. Чаще всего употребляются способ прямой итерации, способ Гаусса-Зейделя, способ последовательной верхней релаксации, градиентные способы наискорейшего спуска и сопряженных градиентов.
Дифференциальные уравнения перемещения (7) интегрируются разными численными способами [5]. В следствии находятся узловые перемещения. Через них определяются все другие искомые величины так же, как функции времени.
Конечно-элементные модели смогут быть нелинейными. Модель деформирования физически нелинейна, в случае, если в ней учитывается нелинейное поведение материала — нелинейная упругость, текучесть, ползучесть и др. Геометрическая нелинейность при деформировании обусловлена большими перемещениями и большими деформациями.
Нелинейные задачи решаются итерационными способами, наряду с этим на каждой итерации рассматриваются квазилинейные уравнения. В практических вычислениях довольно часто используется способ Ньютона- Рафсона и его модификации [5]. Для нелинейных задач деформирования время от времени действенны способы переменных параметров упругости, начальных деформации? и начальных напряжении?. В случае, если в нелинейной задаче серьёзна история нагружения, необходимо создавать ответ малыми шагами нагрузки.