ной функции µ (j? )* ? (j?) по петле обратной связи при трансформации ? от 0
до ? не охватывает точку с координатами (+1;j0), гдеµ (j? ) -передаточная
функция усилителя; ? (j?) — передаточная функция цепи обратной связи .
Для расчёта передаточной функции ) ? (j?) =µ (j? )* ? (j?) электрическую
цепь нужно преобразовать: порвать цепь обратной связи на входе уси-
лителя и замкнуть входные полюса фильтра.
24. Добротность и её влияние на избирательные особенности электрического фильтра.
Добро?тность — параметр колебательной совокупности, определяющий ширину резонанса и характеризующий, во какое количество раз запасы энергии в совокупности больше, чем утраты энергии за один период колебаний.
Добротность обратно пропорциональна скорости затухания собственных колебаний в совокупности. Другими словами, чем выше добротность колебательной совокупности, тем меньше утраты энергии за любой период и тем медленнее затухают колебания.
Чем меньше активное сопротивление цепи, тем меньше утраты энергии в ней и тем больше добротность контура.
Чем меньше активное сопротивление, тем Выше добротность и лучше фильтрация
Добротность — добротность полосового фильтра определяется как отношение резонансной частоты к полосе пропускания .
25. Как по графику переходной характеристики h(t) выяснить добротность активного звена фильтра.
?/логарифмический декримент затухания
В случае, если имеется какое-нибудь устройство либо линия передач и известны его часотные характеристики, возможно, задавая сигнал на входе, взять выходной сигнал. Для этого необходимо взять спектр сигнала, после этого разглядеть, как на него воздействуют частотные характеристики устройства и тем самым взять спектр выходного сигнала. После этого обратным преобразованием Фурье получается сам выходной сигнал.
К недочётам активных фильтров возможно отнести следующее:
• активные фильтры не смогут трудиться на таких высоких частотах, на ко-
торых операционные усилители уже не могут усиливать сигнал,
• активные фильтры нуждаются в источниках питания,
• вероятна утрата устойчивости режима работы, что может привести к
неограниченному росту токов и напряжений при ограниченном входном воз-
действии.
Диапазон частот пропускаемых фильтром без затухания (с малым затуханием), именуется полосой пропусканияили полосой прозрачности;диапазон частот, пропускаемых с громадным затуханием, именуется полосой затуханияили полосой задерживания.Уровень качества фильтра считается тем выше, чем бросче выражены егофильтрующие свойства, т.е. чем посильнее возрастает затухание А р в полосе задерживания. Параметр А р именуется рабочим затуханием, что вводится
вместо коэффициента затухания a при отсутствии согласования на выходе и входе фильтра
Дифференциальный коэффициент усиления операционного усилителя
K=DU вых/DU вх
имеет конечную величину, которая лежит в пределах от 104 до105
Он именуется кроме этого собственным коэффициентом усиления
операционного усилителя, т. е. усиления при отсутствии обратной связи.
Передаточная функция это отношение изображения по Лапласу выходной величины изображению по Лапласу входной величины фильтра.
.
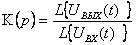(2.40)
В общем случае фильтр возможно разглядывать как четырехполюсник с передаточной функцией
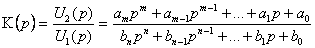, (2.41)
где U1(p) U2(p) – входное и выходное напряжение четырехполюсника в операторной форме; a и b – вещественные постоянные размеры; m, n = 1,2,3, …; n – определяет порядок фильтра.
Для установившейся частоты р = j? и передаточную функцию возможно привести к виду
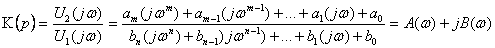. (2.42)
Модуль передаточной функции (2.42) именуется амплитудно-частотной чёртом
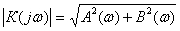. (2.43)
Фазо-частотная черта кроме этого возможно отыскана из (2.42) и представлена в виде
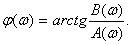(2.44)
Диапазон ?? = ?2 –?1 (рис. 2.23, в) либо полосы частот, в которых проходят сигналы, именуются полосами пропускания. В полосе пропускания значение коэффициента передачи фильтра довольно громадно, а в совершенном случае неизменно. Для полосового фильтра частоты ?1 и ?2 определяются при спаде коэффициента передачи на 3 дБ.
Диапазон частот ?? = ?2 –?1 (рис. 2.23,г), в которых сигналы подавляются, образуютполосу задержания. В полосе задержания коэффициент передачи фильтра довольно мелок, а в совершенном случае равен нулю. Для заграждающего фильтра частоты ?1 и ?2 определяются при спаде коэффициента передачи на 3 дБ.
Частота среза ?ср (fср ) – частота на которой отмечается спад коэффициента передачи на 3 дБ если сравнивать с коэффициентом передачи на нулевой (для ФНЧ) либо нескончаемой (для ФВЧ) частоте.
Резонансная частота fР – частота, на которой коэффициент передачи фильтра имеет большое значение (для полосового фильтра) либо минимальное значение (для заграждающего фильтра).
Добротность — добротность полосового фильтра определяется как отношение резонансной частоты к полосе пропускания .
По виду спектры бывают дискретными (линейчатыми) либо целыми.
Дискретным есть спектр, у которого возможно выделить отдельные составляющие.Целым есть спектр, у которого нельзя выделить отдельные составляющие, поскольку они расположены так близко, что сливаются между собой.