Мы будем разглядывать евклидовое векторное линейное пространство, в котором изучаются прямая плоскость и линия.
При изучении линейного пространства было введено понятие подпространства, определенное как линейное пространство, состоящее, возможно, из меньшего числа базовых векторов. Это указывает, что все свойства пространства выполняются и для подпространства. В частности, любое подпространство должно содержать нуль-вектор. В случае, если в линейном пространстве введена совокупность координат, то не любая прямая плоскость и линия образуют подпространство. Ими будут плоскость и прямая, проходящие через начало. Данный факт показывает, что для изучения разных плоскостей и видов прямых нужно введение координатной совокупности.
Пускай на плоскости зафиксирована декартова совокупность координат Oxy и задана в ней прямая l (рис. V.4). Пускай дан ненулевой вектор перпендикулярный прямой l, другими словами . Вектор назовем обычным (либо нормалью) для прямой l. Все другие обычные векторы к l будут коллинеарны вектору .
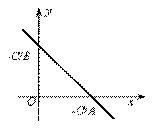
Рис. V.4.
Пускай точка – точка на прямой. Каждая из точек прямой владеет тем свойством, что векторы и перпендикулярны, исходя из этого их скалярное произведение
. (V.1)
Так как , то из формулы (V.1) приобретаем
либо
где .
Уравнение именуется неспециализированным уравнением прямой, поскольку всякое уравнение вида (V.2) определяет прямую, и напротив.
Разглядим линейную функцию двух переменных. Пускай ее вид
. (V.3)
Но данной функции «тесно» на плоскости. Пускай дано линейное векторное трехмерное пространство ?. Введем декартову совокупность координат Oxyz и по аналогии с прошлым зададим обычный вектор . Потому, что областью определения уравнения (V.3) есть геометрическая плоскость, то уравнение (V.3) определяет плоскость P в пространстве и .
По окончании задания точки , учитывая условие перпендикулярности векторов, для любой точки , лежащей на плоскости P, подобно будем иметь
обозначая , приобретаем уравнение (V.3), которое назовем неспециализированным уравнением плоскости. Так, по заданному точке и нормальному вектору на прямой l мы конкретно можем выяснить прямую на плоскости и плоскость в пространстве.
Узнаем, как связаны между собой два неспециализированных уравнения, определяющие одну и ту же плоскость либо прямую.
Пускай имеем совокупность
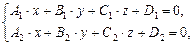 (V.5)
(V.5)
, и ненулевые обычные векторы , . Так как все обычные векторы к заданной точке коллинеарны, то их координаты пропорциональны, то допустим, к примеру,
либо, что то же самое,
, , , .
Умножая второе уравнение формулы (направляться.5) на t и складывая с первым, возьмём
.
Вывод: коэффициенты неспециализированных уравнений одной плоскости пропорциональны.
Определение. Неспециализированное линейное уравнение именуется полным в случае, если все его коэффициенты ненулевые.
Пример V.3. 1) По внешнему виду уравнения (V.5) смогут быть полными.
2) Уравнение плоскости (рис. V.5)
соответствует определению и потому полное.
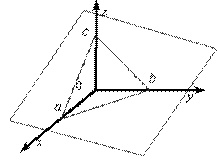
Рис. V.5
Пример V.4.Составить уравнение плоскости, проходящей через точку и перпендикулярной вектору .
Ответ.Применяя формулу (V.4), имеем , откуда по окончании преобразований возьмём .
Это уравнение первой степени и имеется искомое уравнение плоскости.