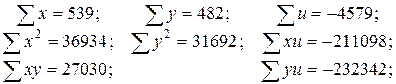
В диапазоне B16:D18 составить матрицу совокупности уравнений (IX.1): в ячейку B16 записать формулу =A13, в ячейку C16 – формулу =A12, в ячейку D16 – формулу =C12, в ячейку B17 – формулу =A12, в ячейку C17 – формулу =B12, в ячейку D17 – формулу =E12, в ячейку B18 – формулу =C12, в ячейку C18 – формулу =E12, в ячейку D18 – формулу =D12. В диапазоне F16:F18 составить вектор свободных участников совокупности уравнений (IX.1): в ячейку F16 записать формулу =F12, в ячейку F17 – формулу =G12, в ячейку F18 – формулу =H12.
Эти значения записывают совокупность уравнений (IX.1) в матричной форме (IX.2):
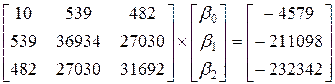 ,
,
Для матричных операций в Excel предусмотрены функции, входящие в категорию «Математические»:
МОПРЕД – вычисление определителя матрицы;
МОБР – вычисление обратной матрицы;
МУМНОЖ – перемножение матриц.
Первая из этих функций возвращает число, исходя из этого вводится как простая формула. Остальные функции возвращают блок ячеек, исходя из этого они должны вводиться как табличные формулы. Первая буква «М» в заглавии трех функций – сокращение от слова «матрица».
В ячейке A17 вычисляется определитель матрицы совокупности =МОПРЕД(B16:D18), что отличен от нуля и равен 656509376.
В блок B20:D22 ввести формулу для вычисления обратной матрицы. Для этого выделить блок B20:D22 (он имеет три строки и три столбца, как и исходная матрица). Ввести формулу {=МОБР(B16:D18)}. Кроме того если Вы используете Мастер функций, необходимо завершить ввод нажатием комбинации клавиш Ctrl+Shift+Enter (вместо щелчка по кнопке OK). Если Вы забыли предварительно выделить блок B16:D18, а ввели формулу в ячейку B20 как простую формулу Excel (завершив ввод нажатием Enter), то не требуется вводить ее заново: выделите B16:D18, надавите клавишу F2 (редактирование), но не изменяйте формулу, Ctrl+Shift+Enter.
В блок F20:F22 ввести для вычисления коэффициентов ?0, ?1 и ?2 формулу {=МУМНОЖ(B20:D22;F16:F18)}, другими словами по окончании решения матричного уравнения взять: ?0= –621,04; ?1 = 4,78; ?2 = –1,96. Подставляя эти значения в уравнение , возможно вычислить значения отметок плоскости тренда ( ) для разности и каждой скважины , характеризующие составляющие случайной изменчивости гипсометрической поверхности.
Уравнение функция от двух координат (условных координат площади) обрисовывает поверхность отметки подошвы меловых отложений. Пускай нужно выстроить эту поверхность, лежащую в диапазонах: [0; 100], [0; 100] с шагом ? = 10 для обеих переменных.
Ввести значения переменной х в столбец A. Для этого в ячейку А26 ввести знак х. В ячейку А27 вводится первое значение довода – левая граница диапазона (0). В ячейку A28 вводится второе значение довода – левая граница диапазона плюс ход построения (10). После этого, выделив блок ячеек А27:А28, автозаполнением взять все значения довода (за правый нижний угол блока протянуть до ячейки А37).
Значения переменной y вводим в строчок 26. Для этого в ячейку В26 вводится первое значение переменной – левая граница диапазона (0). В ячейку С26 вводится второе значение переменной – левая граница диапазона плюс ход построения (10).После этого, выделив блок ячеек В26:С26, автозаполнением взять все значения довода (за правый нижний угол блока протягиваем до ячейки L26).
Потом ввести значения переменной . Для этого табличный курсор нужно поместить в ячейку В27 и записать формулу =$F$20+$F$21*$A27+$F$22*B$26. Обращаем внимание, что знаки $ предназначены для фиксации адреса столбца А – переменной х и строки 26 – переменной у. Помимо этого, знаки $ предназначены для фиксации адресов коэффициентов ?0 – $F$20, ?1 – $F$21 и ?2 – $F$22. Надавить кнопку ОK. Сейчас нужно скопировать функцию из ячейки В27. Для этого автозаполнением (протягиванием вправо) эту формула копируется сначала в диапазон B27:L27, по окончании чего (протягиванием вниз) – в диапазон B28:L37.
Для построения диаграммы нужно выделить диапазон A26:L37и на панели инструментов Стандартная нужно надавить кнопку Мастер диаграмм. В показавшемся диалоговом окне Мастер диаграмм (ход 1 из 4): тип диаграммы указать тип диаграммы – Поверхность, и вид – Контурная диаграмма (левую нижнюю диаграмму в правом окне). По окончании чего нажимаем кнопку Далеев диалоговом окне.
В показавшемся диалоговом окне Мастер диаграмм (ход 2 из 4): источник данных диаграммы нужно выбрать вкладку Диапазон разрешённых и убедиться, что в поле Диапазон указан верно промежуток данных $A$26:$L$37.
Потом нужно указать в строчках либо столбцах расположены последовательности данных. Это выяснит ориентацию осей х и у. В примере тумблер Последовательности в посредством указателя мыши установить положение в столбцах.
Выбрать вкладку Последовательность и в поле Подписи оси Х проверить диапазон автографов оси х – $A$27:$A$37.
Проверить кроме этого значения автографов оси у. Для этого в рабочем поле Рядуказать первую запись 0и в рабочее поле Имя, активизировав его указателем мыши, проверить первое значение переменной у –$B$26. После этого в поле Рядуказать вторую запись 10 и в рабочем поле Имяувидим второе значение переменной у –$С$26, в поле Подписи оси Х проверить диапазон автографов оси х – $A$27:$A$37 Повторить, так, до последней записи – 100. По окончании нужно надавить кнопку Потом.
В третьем окне требуется ввести названия осей и заголовок диаграммы. Для этого нужно выбрать вкладку Заголовки, щелкнув на ней указателем мыши. Щелкнув в рабочем поле Наименование диаграммы указателем мыши, ввести с клавиатуры в поле наименование: Карта отметок подошвы меловых отложений. После этого подобным образом ввести в рабочие поля Ось Х (категорий), Ось Y (последовательностей данных) и Ось Z (значений) соответствующие заглавия X, км, Y, км, Полные отметки, м. Потом направляться надавить кнопку Готово, и по окончании маленького редактирования будет взята диаграмма (см. рис. IX.1) изолиний плоскости тренда.
Оценка степени приближения плотности тренда к наблюденным итогам, другими словами средняя изменчивость их отклонений возможно охарактеризована величиной SSDD = SST – SSR,
где 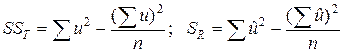 .
.
Процент учета неспециализированной изменчивости плоскостью тренда осуществляется по формуле 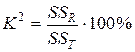 .
.
В ячейку I1 ввести обозначение u’, в ячейку J1 ввести обозначение u^2, в обозначение и1 – ячейку u’^2. Диапазон I2:I11 заполнить значениями отметок подошвы меловых отложений, вычисленными по формуле тренда: в ячейку I2 ввести формулу =$F$20+$F$21*A2+$F$22*C2, которую скопировать во целый диапазон I2:I11. В ячейку J2 ввести формулу =F2^2, которую скопировать во целый диапазон J2:J11. В ячейку K2 ввести формулу =I2^2, которую скопировать во целый диапазон K2:K11. В ячейках диапазона I12:K12 вычислить посредством кнопки Автосумма панели инструментов Стандартная соответствующие суммы по столбцам. В ячейку J14 ввести обозначение SST, в ячейку J15 ввести обозначение SSR, ячейку J16 ввести обозначение SSDD, ячейку J17 ввести обозначение K^2. В ячейку K14 ввести формулу =J12-(F12^2/A13), в ячейку K15 ввести формулу =K12-(I12^2/A13), в ячейку K16 ввести формулу =K14-K15, в ячейку K17 ввести формулу =K15/K14 и установить формат числа в процентах (кнопка Процентный формат на панели инструментов Форматирование).
Так, плоскость тренда учитывает 90% неспециализированной изменчивости:
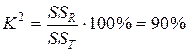 .
.
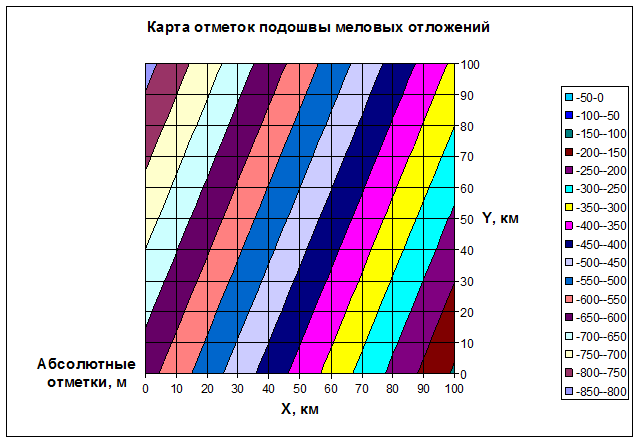
Рис. IX.1. Карта отметок подошвы меловых отложений в северо-восточной Африке: поверхность тренда первого порядка
Примечание
В приведенном ПРИМЕРЕ IX.1 задача аппроксимации поверхности тренда удовлетворительно решается с применением ортогональных полиномов первой степени. В случаях, в то время, когда часть случайной изменчивости остается все же достаточно большей по окончании аппроксимации линейными функциями, для обнаружения закономерной изменчивости более большого порядка используются полиномы второй, третьей и реже – более высоких степеней.
Поверхность тренда второго порядка будет описываться уравнением , а число малоизвестных полиномиальных коэффициентов увеличится до пяти. Для перехода к уравнению следующего более большого порядка любая географическая координата возводится в заданную степень и добавляются соответствующие смешанные произведения.
Выбор степени аппроксимирующего полинома и оценка значимости распознанных закономерностей смогут осуществляться посредством дисперсионного анализа. Для этого подсчитываются средние квадраты отклонений эмпирических значений исследуемого показателя в точках замера от среднего арифметического и от аппроксимирующих поверхностей различного порядка, и средние квадраты отклонений от среднего арифметического самих аппроксимирующих поверхностей. Значимость закономерностей, обрисовываемых полиномами определенного порядка, проверяется посредством критерия Фишера.
В геологической практике региональные закономерности в большинстве случаев удовлетворительно описываются полиномами не выше третьей степени.
Аппроксимация тригонометрическими полиномами разрешает обрисовывать закономерные периодические колебания особенностей геологических объектов.
Из всех вероятных аппроксимирующих функций выбирается та, которая правильнее обрисовывает имеющиеся эти и содержит мельчайшее число параметров. Но вид таковой функции нельзя предсказать заблаговременно, что значительно затрудняет применение на практике данных моделей. Аппроксимирующие функции координат пространства как модели геологических объектов имеют и другие недочёты:
- допускают существование нереальных значений изучаемых переменных, к примеру, отрицательных значений содержания химических элементов в породах либо мощностей рудных тел;
- не учитывают резких, быстрых трансформаций значений изучаемого свойства по геологическим границам, благодаря чего при моделировании рудных тел высокие содержания нужного компонента время от времени распространяются на заведомо безрудные породы, к примеру, на пострудные дайки;
- негодны при применении их для описания прерывистых объектов (к примеру, рудных тел с прерывистым характером оруденения), так как происходит сглаживание данных и искажается представление о степени прерывистости (возрастает коэффициент рудоносности).
Выделение аномальных значений изучаемого свойства имеет в геологии громадное практическое значение, поскольку с «странностями» довольно часто связаны тела нужных ископаемых и другие самые интересные геологические объекты.
ЗАДАЧА IX.1
Требуется
Построитьсхему размещения пробуренных скважин – рис. VIII.2.
Указание
Применять кнопку Мастер диаграмм панели инструментов Стандартная, выбрав тип диаграммы – Точечная.
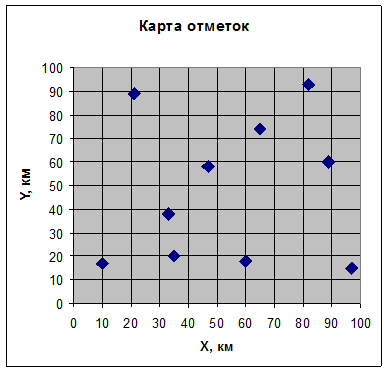
Рис. IX.2. Карта отметок подошвы меловых отложений в северо-восточной Африке: размещение скважин с замерами полных отметок подошвы меловых отложений
ПРИМЕР IX.2
Требуется
По исходным данным ПРИМЕРА IX.1 и табл. IX.1. произвести аппроксимацию поверхностей тренда полиномом в пакете Excel посредством функции ЛИНЕЙН либо посредством процедуры Регрессия из пакета анализа данных.
Ответ
Задача нахождения полиномиальных коэффициентов функции , обрисовывающей поверхность тренда, возможно решена несложнее посредством функции Excel ЛИНЕЙН либо посредством процедуры Регрессия из пакета анализа данных.
В ячейку A1 ввести обозначение x, в ячейку B1 ввести обозначение y, в ячейку C1 – обозначение u. Диапазон A2:A11 заполнить значениями координат скважин x, диапазон B2:B11 заполнить значениями координат скважин y, диапазон C2:C11 заполнить значениями полных отметок подошвы меловых отложений u из табл. IX.1.
При применении функции ЛИНЕЙН в вольный диапазон G2:I6 ввести табличную формулу {=ЛИНЕЙН(C2:C11;A2:B11;1;1)}. Первая строчок взятого массива данных – это и имеется соответствующие полиномиальные коэффициенты: в ячейке I2 – ?0, в ячейке H2 – ?1 и в ячейке G2 – ?2. Ячейка G4 взятого массива данных содержит коэффициент детерминации R2, что равен 0,900. Следовательно, модель в целом адекватна обрисовываемому явлению.
Построение диаграммы поверхности тренда возможно осуществить подобно тому, как это сделано в ПРИМЕРЕ IX.1.
При применении процедуры Регрессия из пакета анализа данных в пункте меню Сервис выберите строчок Анализ данных и потом укажите курсором мыши на строчок Регрессия.
В показавшемся диалоговом окне задайте Входной промежуток Y. Для этого наведите указатель мыши на верхнюю ячейку столбца зависимых данных (C1), надавите левую кнопку мыши и, не отпуская ее, протяните указатель мыши к нижней ячейке (C11), после этого отпустите левую кнопку мыши. (Обратите внимание, что зависимые эти – это те эти, каковые предполагается вычислять). Так же укажите Входной промежуток X, другими словами введите ссылку на диапазон свободных данных A1:B11. (Свободные эти – это те эти, каковые будут измеряться либо наблюдаться).
Установите флажок в поле Метки в первой строке. Установите флажок в поле График подбора. Потом укажите выходной диапазон. Для этого поставьте тумблер в положение Выходной промежуток (наведите указатель мыши и щелкните левой кнопкой), после этого наведите указатель мыши на правое поле ввода Выходной промежуток и, щелкнув левой кнопкой мыши, указатель мыши наведите на левую верхнюю ячейку выходного диапазона (A31). Щелкните левой кнопкой мыши. Надавите кнопку OK.
Результаты анализа. В выходном диапазоне покажутся графики и результаты подбора и остатков.
Интерпретация результатов. В таблице Дисперсионный анализ оценивается неспециализированное уровень качества взятой модели ее достоверность по уровню значимости критерия Фишера – р, что должен быть меньше, чем 0,05 (строчок Регрессия, столбец Значимость F, в примере 0,0003, другими словами p =0,0003 – модель значима, и степень точности описания моделью процесса – R-квадрат (вторая строчок сверху в таблице Регрессионная статистика, в примере R-квадрат = 0,900. Следовательно, модель в целом адекватна обрисовываемому явлению.
Потом нужно найти значения коэффициентов модели. Они определяются из таблицы в столбце Коэффициенты – в строчке Y-пересечение приводится вольный член, в строчках соответствующих переменных приводятся значения коэффициентов при этих переменных. В столбце p-значениеприводится достоверность отличия соответствующих коэффициентов от нуля. В случаях, в то время, когда р 0,05, коэффициент может принимать во внимание нулевым. Это указывает, что соответствующая свободная переменная фактически не воздействует на зависимую переменную и коэффициент возможно убран из уравнения. Все вычисленные коэффициенты значимы.
Так, функция , обрисовывающая поверхность тренда, возможно записана как .
ЗАДАЧА IX.2
Требуется
По исходным данным ПРИМЕРА IX.1 и табл. IX.1. произвести аппроксимацию поверхностей тренда полиномом в пакете Excel посредством функции ЛИНЕЙН либо посредством процедуры Регрессия из пакета анализа данных.
Указание
Поверхность тренда второго порядка будет описываться уравнением , а число малоизвестных полиномиальных коэффициентов увеличится до пяти.
Диапазон A2:A11 заполнить значениями координат скважин x, диапазон B2:B11 заполнить значениями квадратов координат скважин x2, диапазон C2:C11 заполнить значениями координат скважин y, диапазон D2:D11 заполнить значениями координат скважин y2, диапазон E2:E11 заполнить произведениями значений координат скважин xy, диапазон F2:F11 заполнить значениями безотносительных отметок подошвы меловых отложений u из табл. IX.1.
Диаграмма изолиний плоскости тренда второго порядка – см. рис. IX.3.
Данные для построения данной диаграммы возможно разместить следующим образом – рис. IX.4.
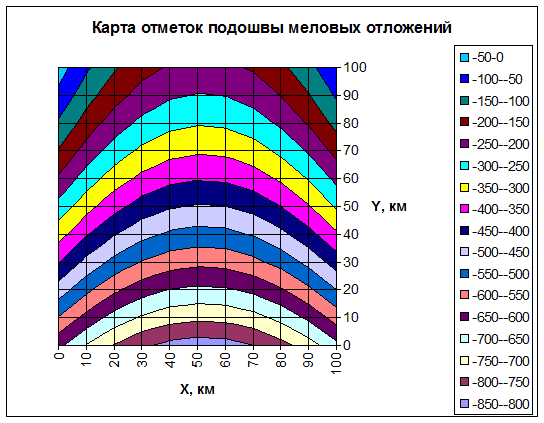
Рис. IX.3. Карта отметок подошвы меловых отложений в северо-восточной Африке: поверхность тренда второго порядка
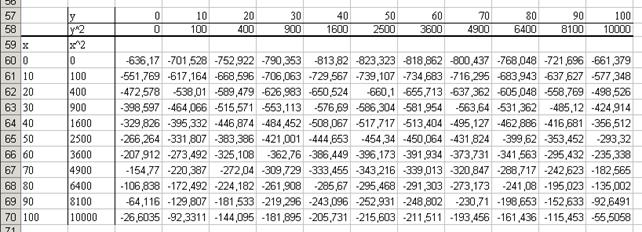
Рис. IX.4. Размещение исходных на рабочем странице для построения диаграммы рисунка IX.3
ОБЛАСТИ ПРИМЕНЕНИЯ ГОРНО-ГЕОМЕТРИЧЕСКИХ В МОДЕЛЕЙ И ТРЕНД-АНАЛИЗА В ГЕОЛОГИИ
Большая часть геологических задач относится к числу пространственных изучений и имеет цель распознать особенности размещения изучаемых геологических объектов в структурах земной коры либо элементов ее строения. Исходя из этого способы математического моделирования и количественного описания пространственных геологических закономерностей являются ведущими во всех отраслях геологических наук.
В геологической практике с покон веков только обширно распространены способы горно-геометрического моделирования геологических свойств и тел горных пород и нужных ископаемых.
Графические модели разных особенностей природных геологических тел активно применяются в структурной геологии, геологии нужных ископаемых, рудничной геологии и методике поисков и разведки нужных ископаемых. Способы горно-геометрического моделирования изучаются в курсе геометризации недр. На правилах П.К. Соболевского были созданы разные аналитические способы описания изменчивости, применяющие для этих целей первые либо вторые последовательные разности значений показателей изменчивости по смежным пунктам наблюдений.
Посредством горно-геометрических моделей возможно выразить особенности пространственной изменчивости особенностей геологических образований, установить значение изучаемого свойства в любой точке исследуемого объекта, взять представление об его морфологии и внутреннем строении.
Гипсометрические замыслы поверхностей контактов, не выходящих на поверхность интрузивных рудных залежей и тел, графики изолиний содержаний нужных компонентов в рудных телах, карты химических и геофизических полей активно применяются в геологической практике, поскольку они снабжают наглядность изображения и улучшают пространственное восприятие изучаемых закономерностей. Но плавности изменения и требование непрерывности изучаемого свойства ограничивает область их использования на практике объектами с очень выдержанными в пространстве особенностями. К таким объектам относятся пласты осадочных пород, границы интрузивных образований, рудные тела с несложной морфологией и довольно равномерным характером оруденения и т.п.
ЛАБОРАТОРНАЯ РАБОТА № X. ОПТИМИЗАЦИЯ
ГЛАВНЫЕ ПОНЯТИЯ
Под оптимизацией знают процесс выбора наилучшего варианта из всех вероятных. С позиций инженерных расчетов способы оптимизации разрешают выбрать наилучший вариант конструкции, наилучшее распределение ресурсов и т.п.
В ходе ответа задачи оптимизации в большинстве случаев нужно отыскать оптимальные значения некоторых параметров, определяющих данную задачу. При ответе инженерных задач их принято именовать проектными параметрами, а в экономических задачах их в большинстве случаев именуют параметрами замысла. В качестве проектных параметров смогут быть, например, значения линейных размеров объекта, массы, температуры и т.п. Число п проектных параметров x1, x2, …, xn характеризует размерность (и степень сложности) задачи оптимизации.
Выбор оптимального ответа либо сравнение двух других ответов проводится посредством некоей зависимой величины (функции), определяемой проектными параметрами. Эта величина именуется целевой функцией (либо критерием качества). В ходе ответа задачи оптимизации должны быть отысканы такие значения проектных параметров, при которых целевая функция имеет минимум (либо максимум). Так, целевая функция – это глобальный критерий оптимальности в математических моделях, благодаря которым описываются инженерные либо экономические задачи.
Целевую функцию возможно записать в виде
u = f(x1, x2, …, xn). (X.1)
Примерами целевой функции, видящимися в инженерных и экономических расчетах, являются прочность либо масса конструкции, мощность установки, количество выпуска продукции, цена перевозок грузов, прибыль и т.п.
При одного проектною параметра (n = 1) целевая, функция (X.1) есть функцией одной переменной, и ее график – некая кривая на плоскости. При п = 2 целевая функция есть функцией двух переменных, и ее графиком есть поверхность.
направляться подчернуть, что целевая функция не всегда возможно представлена в виде формулы. Время от времени она может принимать лишь кое-какие дискретные значения, задаваться в виде таблицы и т.п. В любых ситуациях она должна быть однозначной функцией проектных параметров.
Целевых функций возможно пара. К примеру, при проектировании изделий машиностроения в один момент требуется обеспечить большую надежность, минимальную материалоемкость, большой нужный количество (пли грузоподъемность). Кое-какие целевые функции могут быть несовместимыми. В таких случаях нужно вводить приоритет той либо другой целевой функции.
ЗАДАЧИ ОПТИМИЗАЦИИ
Возможно выделить два типа задач оптимизации – абсолютные и условные. Абсолютная задача оптимизации пребывает в отыскании максимума либо минимума настоящей функции (X.1) от п настоящих переменных и определении соответствующих значений доводов на некоем множестве ? n-мерного пространства. В большинстве случаев рассматриваются задачи минимизации; к ним легко сводятся и задачи на поиск максимума методом замены символа целевой функции на противоположный.
Условные задачи оптимизации, либо задачи с ограничениями, – это такие, при формулировке которых задаются кое-какие условия (ограничения) на множестве ?. Эти ограничения задаются совокупностью некоторых функций, удовлетворяющих уравнениям либо неравенствам.
Ограничения-равенства высказывают зависимость между проектными параметрами, которая обязана учитываться при нахождении ответа. Эти ограничения отражают законы природы, наличие ресурсов, денежные требования и т.п.
В следствии ограничений область проектирования ?, определяемая всеми п проектными параметрами, возможно значительно уменьшена в соответствии с физической сущностью задачи. Число m ограничений-равенств возможно произвольным. Их возможно записать в виде
g1(x1, x2, …, xn) = 0,
g2(x1, x2, …, xn) = 0, (X.2)
……………………
gm(x1, x2, …, xn) = 0.
Во многих случаях из этих соотношений возможно выразить одни проектные параметры через другие. Это разрешает исключить кое-какие параметры из процесса оптимизации, что ведет к уменьшению размерности задачи и облегчает ее ответ. Подобно смогут вводиться кроме этого ограничения-неравенства имеющие вид
a1 ? ?1(x1, x2, …, xn) ? b1,
a2 ? ?2(x1, x2, …, xn) ? b2, (X.3)
…………………………
ak ? ?k(x1, x2, …, xn) ? bk.
направляться отметить особенность в отыскании ответа при наличии ограничений. Оптимальное ответ тут может соответствовать или локальному экстремуму (максимуму либо минимуму) в области проектирования, или значению целевой функции на границе области. В случае, если же ограничения отсутствуют, то ищется оптимальное ответ на всей области проектирования, другими словами глобальный экстремум.
методы и Теория ответа задач оптимизации при наличии ограничений составляют предмет изучения одного из серьёзных разделов прикладной математики — математического программирования.
ОДНОМЕРНАЯ ОПТИМИЗАЦИЯ. ЗАДАЧИ НА ЭКСТРЕМУМ
Одномерная задача оптимизации в общем случае формулируется следующим образом. Отыскать мельчайшее (пли громаднейшее) значение целевой функции y = f(x), заданной на множестве ?, и найти значение проектного параметра , при котором целевая функция принимает экстремальное значение. Существование ответа поставленной задачи вытекает из следующей теоремы.
Теорема Вейерштрасса. Любая функция f(направляться), постоянная на отрезке [a, b], принимает на этом отрезке мельчайшее и громаднейшее значения, другими словами на отрезке [a, b] существуют такие точки x1 и x2, что для любого имеют место неравенства
f(x1) ? f(x) ? f(x2).
Эта теорема не обосновывает единственности ответа. Есть вероятность, в то время, когда равные экстремальные значения достигаются сходу в нескольких точках данного отрезка. В частности, такая обстановка имеет место для периодической функции, разглядываемой на отрезке, содержащем пара периодов.
Будем разглядывать способы оптимизации для различных классов целевых функций. Несложным из них есть случай дифференцируемой функции f(x) на отрезке [a, b],причем функция задана в виде аналитической зависимости y=f(x), и возможно отыскано явное выражение для ее производной f'(x). Нахождение экстремумов таких функций возможно проводить известными из курса высшей математики способами дифференциального исчисления. Напомним кратко данный путь.
Функция f(x) может быть около собственного мельчайшего и громаднейшего значений или в граничных точках отрезка [a, b],или в точках максимума и минимума. Последние точки непременно должны быть критическими, другими словами производная f'(x) в этих точках обращается в нуль, — это нужное условие экстремума. Следовательно, для определения мельчайшего либо громаднейшего значений функции f(x) на отрезке [a, b] необходимо вычислить ее значения во всех критических точках данного отрезка и в его граничных точках и сравнить полученные значения; мельчайшее либо громаднейшее из них и будет искомым значением.