Тумблер Choose observations to maximize initial between-cluster distances.Если Вы выбираете данный тумблер, наблюдения либо объекты будут установлены как начальные центры кластера. (1) программа выберет первые номера кластеров случаев, дабы быть соответствующими центрами кластера; (2) последующие случаи заменят прошлые центры кластера, в случае, если их самое мелкое расстояние к любому из центров кластера больше, чем самое мелкое расстояние между кластерами; в случае, если дело обстоит не так, то (3) последующие случаи заменят начальные центры кластера, в случае, если их самое мелкое расстояние от центра кластера большее расстояние того центра кластера от любого другого центра кластера. Эффект данной процедуры выбора обязан развернуть начальные расстояния между кластерами. Обратите внимание, что эта процедура может выдавать кластеры с единственными (отдельными) наблюдениями, в случае, если имеется ясный outliers в данных.
Тумблер Choose the first N (Number of clusters) observations.Если Вы выбираете данный тумблер, первые номера кластеров наблюдений будут начальными центрами кластера. Так, эта опция снабжает Вас полным контролем над выбором начальной конфигурации. Это довольно часто полезно, если Вы приносите априорные ожидания относительно характера (природы) кластеров к анализу. В этом случае, переместите случаи, каковые Вы желаете выбрать как начальные центры кластера, к началу файла.
Тумблеры Casewise deletion of missing data илиMean substitution в разделе MD deletion, первый направляться применять, в случае, если в анализ направляться включать лишь случаи, каковые имеют для всех переменных все сведенья, второй направляться применять, в то время, когда отсутствующие эти будут заменены средствами для соответствующих переменных (для этого анализа лишь, но не для файла данных). По умолчанию стоит тумблер Casewise deletion of missing data.
Покинуть установленные по умолчанию тумблеры и потом, в диалоговом окне Cluster Analysis: K-means clustering:направляться надавить кнопку OK.
В показавшемся диалоговом окне K-Means clustering Results: надавить кнопку Summary: Clusters means Euclidean distances (рис. VII.19). В следствии расчета возьмём матрицу дистанционных коэффициентов между кластерами вычисленных по евклидовым метрикам (см. рис. VII.20). Тут же рассчитываются средние по всем измерениям для каждого кластера.
Рис. VII.19.Анализ вK-Means clustering Results:
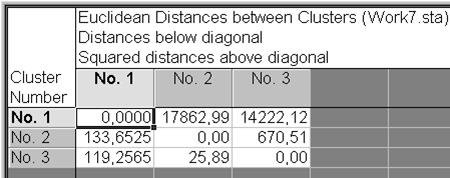
Рис. VII.20.Матрица евклидовых метрик между кластерами
Возвратиться в диалоговое окно K-Means clustering Results: и надавить кнопку Analysis of variance. Анализ вариант направляться применять, в случае, если направляться сравнивать изменчивость в пределах группы (within) (малая, в случае, если классификация хорошая) с изменчивостью между группами (between) (громадная, в случае, если классификация хорошая), другими словами выполнить дисперсионный анализ между группами для каждого измерения (рис. VII.21). Возможно просмотреть результаты дисперсионного анализа, сравнивая для каждого измерения результаты между группами.
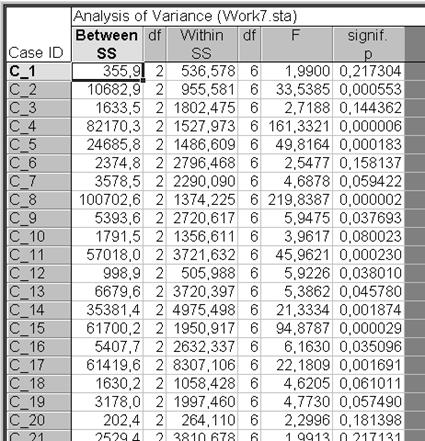
Рис. VII.21. Итог дисперсионного анализа Analysis of variance
Возвратиться в диалоговое окно K-Means clustering Results: и надавить кнопку Graph of means. Результатом будет график средних по кластерам (рис. VII.22).
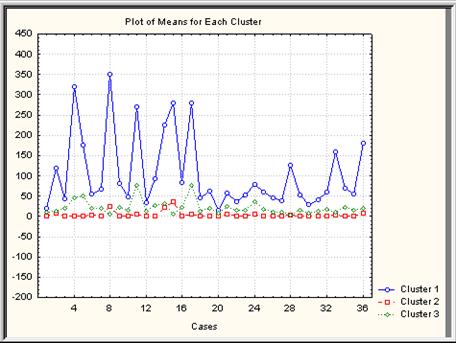
Рис. VII.22.График средних по кластерам
Возвратиться в диалоговое окно K-Means clustering Results: и надавить кнопку Descriptive statistics for each clusterна вкладке Advanced. Результатом будет вывод больших таблиц описательной статистики для каждого измерения по кластерам (рис. VII.23).
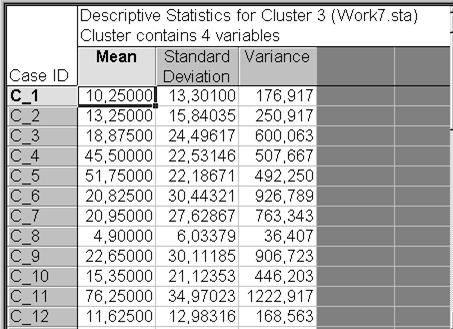
Рис. VII.23. Дескриптивная статистика для третьего кластера
Возвратиться в диалоговое окно K-Means clustering Results: и надавить кнопку Members of each cluster distances. Результатом будет расчет евклидовых расстояний от центров кластеров для каждого элемента входящего в кластер (рис. VII.24). Это разрешает идентифицировать потенциальных «нехороших» участников кластера.
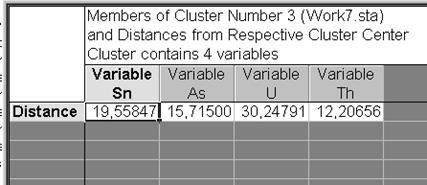
Рис. VII.24. Евклидовы расстояния для каждого кластера
Возвратиться в диалоговое окно K-Means clustering Results: и надавить кнопку Save classifications and distances. Результатом будет краткая электронная таблица содержащая: порядковые номера элементов (1 столбец), номер кластера, в который входит элемент (2 столбец) и евклидовы метрики для каждого элемента от соответствующего центра кластера (3 столбец) – рис. VII.25.
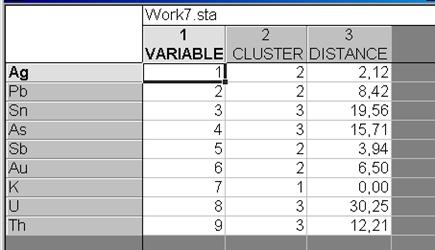
Рис. VII.25.Итог исполнения Save classifications and distances
7. Совершить факторный анализ для выделения ассоциаций химических элементов. Для этого в меню с главными процедурами Statistics выбрать Multivariate Exploratory Techniques, а в показавшемся его меню – Factor Analysis.
В показавшемся диалоговом окне Factor Analysis: (см. рис. VII.26) на вкладке Quick надавить кнопку Variables и показавшемся диалоговом окне Select the variables for the factor analysis надавить кнопку Select All (рис. VII.27). Возвратиться в диалоговое окно Factor Analysis: и надавить кнопку OK (рис. VII.28).
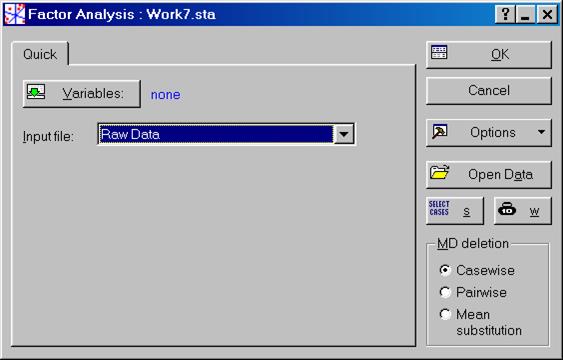
Рис. VII.26. Диалоговое окно Factor Analysis:
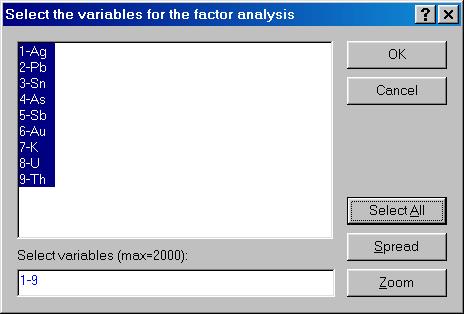
Рис. VII.27.Выбор переменных для факторного анализа
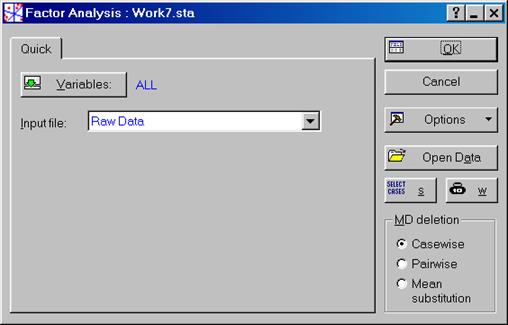
Рис. VII.28. Диалоговое окно Factor Analysis: с выбранными переменными
Покажется окно Define Method of Factor Extraction:, где выбираем на вкладке Descriptives (рис. VII.29) кнопку Review correlations, means, standard deviations. В диалоговом окне Review descriptive statistics(рис. VII.30) нажимаем кнопку Correlations. Результатом расчета будет корреляционная матрица (рис. VII.31). Она подобна матрице, взятой в разделе корреляционного анализа и представленной на рис. VII.4.
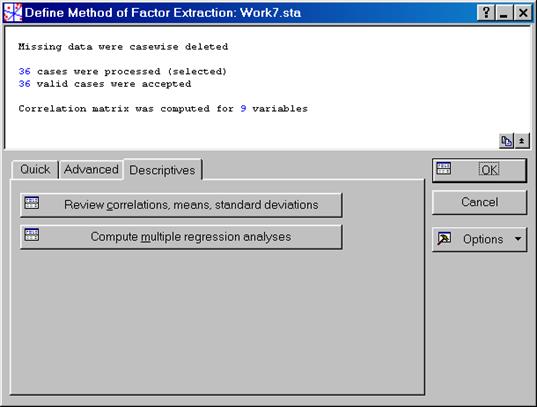
Рис. VII.29. Диалоговое окно Define Method of Factor Extraction:
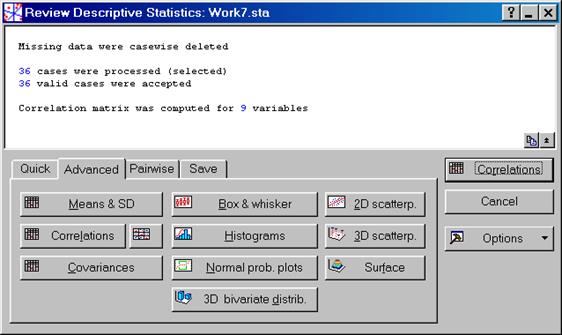
Рис. VII.30.Диалоговое окноReview descriptive statistics
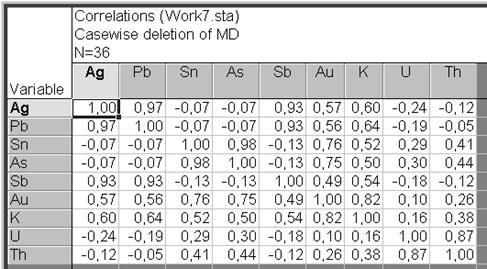
Рис. VII.31.Корреляционная матрица
В диалоговом окне Review descriptive statistics нажимаем кнопку Cancel и возвращаемся в диалоговое окно Define Method of Factor Extraction:, где выбираем на вкладке Advancedв разделе Extraction method установленный по умолчанию способ Principal Components (способ основных компонент либо факторов). В разделе Max no. of factors установить число 9 – предельное количество факторов в нашем случае, в разделе Mini. eigenvalue: 0 – минимальное значение для данной опции (рис. VII.32). Надавить кнопку OK. Раскрывается диалоговое окно Factor Analysis Results:, в котором выбирается вкладка Quick, где нажимается кнопка Eigenvalues (личные значения) (рис. VII.33). Результатом расчета будет таблица Eigenvalues (частей от общего числа факторов, в этом случае – части от девяти), которая содержит следующие столбцы: личные значения (Eigenvalues), проценты от полной величины (% Total variance), кумулятивных собственных значений (Cumulative Eigenvalues), и кумулятивного процента (Cumulative %) (рис. VII.34). Первые три фактора дают солиднейший вклад в процентном отношении. Основываясь на таблице Eigenvalues, возможно предложить разглядывать лишь эти три фактора.
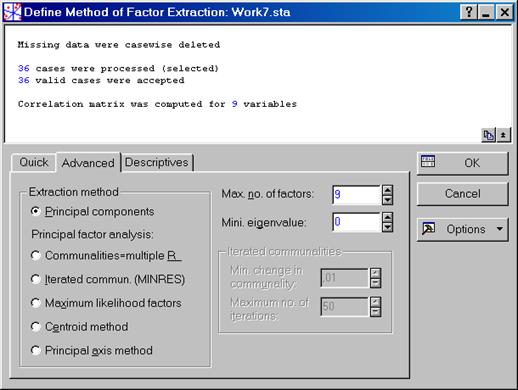
Рис. VII.32. Выбор параметров в диалоговом окне Define Method of Factor Extraction:
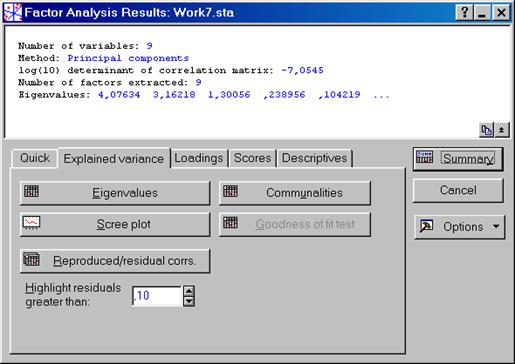
Рис. VII.33. Расчет Explained variance в диалоговом окне Factor Analysis Results:
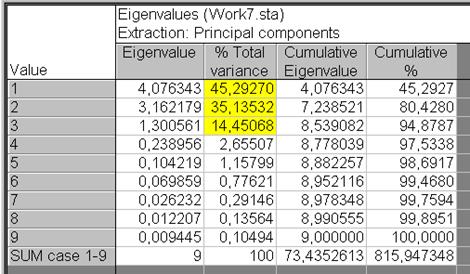
Рис. VII.34. Расчетная таблица Eigenvalues
В диалоговом окне Factor Analysis Results: выбрать вкладку Explained variance, где надавить кнопку Scree plot. Результатом будет график, основанный на тесте Каттелла (рис. VII.35), иллюстрирующий первый столбец таблицы Eigenvalues. Основанный на способе Монте-Карло, Cattell’s scree test предлагает, что в точке, где постоянное падение Eigenvalues выравнивается, предлагается сокращение остальных дополнительных факторов, так когда случайный «шум» добавляется дополнительными факторами. В отечественном примере, эта точка возможно для фактора 3 либо фактора 4. Исходя из этого необходимо попытаться оба решения и разглядеть тот, что выдаст самый поддающееся толкованию ответ.
Сейчас исследуем факторные нагрузки. Сперва направляться разглядеть невращаемые факторные нагрузки для всех 9 факторов. В диалоговом окне Factor Analysis Results: выбрать вкладку Loadings и в разделе Factor rotation: выбрать установленное по умолчанию – Unrotated. Обратите внимание, что считается, что факторы со значением нагрузки более 0,70 – факторы с высокой нагрузкой. После этого надавить на кнопку Summary (рис. VII.36). Результатом расчета будет таблица факторных нагрузок упорядоченных так, дабы последующие факторы составляли все меньшее и меньшее количество отличия (рис. VII.37). Не страно видеть, что первый фактор показывает большая часть самых высоких нагрузок.
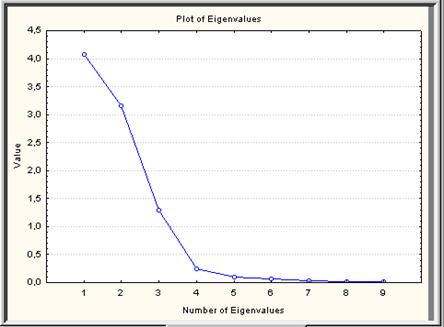
Рис. VII.35. График Scree plot
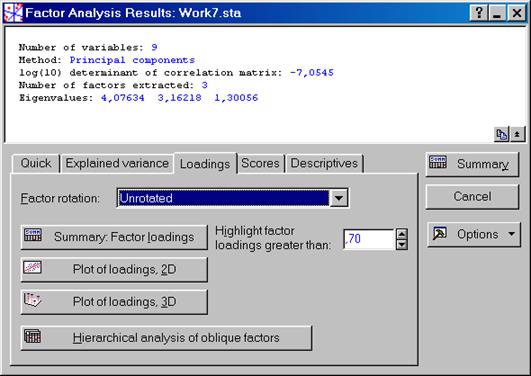
Рис. VII.36. Выбор Unrotated в диалоговом окне Factor Analysis Results: на вкладке Loadings в разделе Factor rotation:
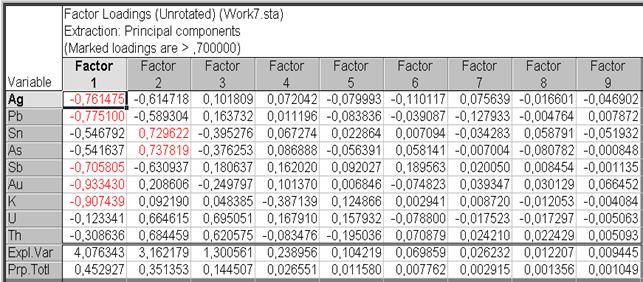
Рис. VII.37. Таблица факторных нагрузок по способу Unrotated для 10 факторов
Фактическая ориентация факторов в пространстве факториала произвольна и все вращения факторов в пространстве воспроизведут корреляции одинаково отлично. Исходя из этого предложено вращать факторы так, дабы выдать такую структуру фактора, что ее несложнее трактовать. Такая несложная структура и была выяснена Thurstone (1947), дабы по большей части обрисовать состояние, в то время, когда факторы отмечены высокими нагрузками для некоторых переменных, низкими нагрузками для других, и в то время, когда есть немного высоких перекрестных нагрузок, то есть немного переменных с значительными нагрузками на больше, чем один фактор. Популярный обычный вычислительный способа вращения, для получения простой структуры – VARIMAX вращение (Kaiser, 1958); Другие, каковые были предложены — QUARTIMAX, BIQUARTIMAX, и EQUAMAX (см. Harman, 1967) – все они осуществлены в STATISTICA.
Сперва разглядим число факторов, которое желаем вращать. Было предварительно решено, что три фактора являются самые влиятельными, но по итогам рассмотрения графика на рис. VII.35 было решено разглядывать четыре фактора. Надавить кнопку Cancel, дабы возвратиться в окно Define Method of Factor Extraction:, где выбрать вкладкуQuick. Установить в разделе Max no. of factors число 4 – число факторов в разглядываемом случае, в разделе Mini. eigenvalue: 0 – минимальное значение для данной опции (рис. VII.38).
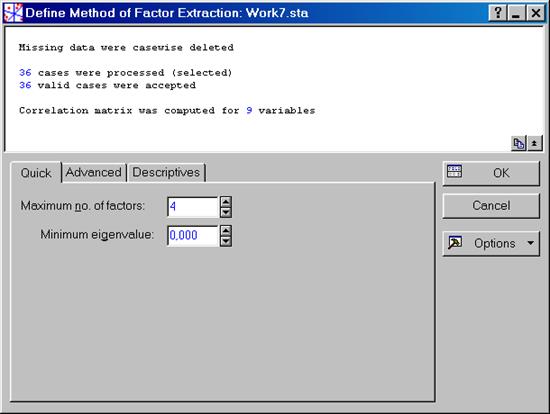
Рис. VII.38. Установка нового числа факторов в Max no. of factors
Надавить кнопку OK. Раскрывается диалоговое окно Factor Analysis Results:, в котором выбрать вкладку Loadings, и в перечне Factor rotation: выбрать Varimax raw (рис. VII.39). После этого надавить на кнопку Summary. Результатом расчета будет таблица Factor Loadings (факторных нагрузок) – см. рис. VII.40. Окажется вращаемое ответ с четырьмя факторами. Четвертый фактор не дает громадных нагрузок. Повторить ответ для трех факторов. Результатом расчета будет таблица Factor Loadings (факторных нагрузок) – см. рис. VII.41. Первый фактор показывает большая часть самых высоких нагрузок. Для золота (Au) громадную нагрузку показывает второй фактор – около 0,82 и достаточно громадную – первый фактор – около 0,55. Фактор 1 связан с Ag, Pb и Sb, фактор 2 – с Sn, As и Au, фактор 3 – с U и Th. С K, думается, связан и фактор 1 и фактор 2: фактор 1 – нагрузка 0,66, фактор 2 – 0,57.
Рис. VII.39. Выбор Varimax raw в диалоговом окне Factor Analysis Results: на вкладке Loadings в разделе Factor rotation:
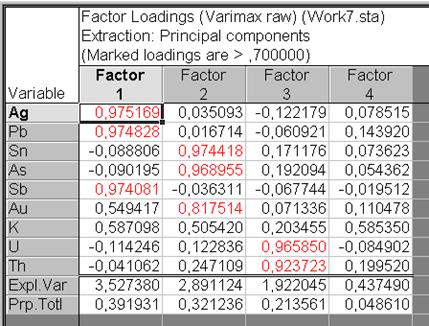
Рис. VII.40. Таблица факторных нагрузок по способу Varimax для 4 факторов
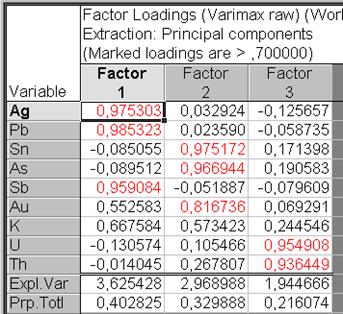
Рис. VII.41. Таблица факторных нагрузок по способу Varimax для 3 факторов
Щелкнуть в диалоговом окне Factor Analysis Results: на вкладке Loadings кнопкойPlot of loadings, 2D. Откроется диалоговое окно Select two factors for the plot, в котором выберем Factor 1 и Factor 2 (рис. VII.42). Надавить OK. Результатом будет плоский график нагрузок (рис. VII.43). Подобно выстроить график нагрузок для Factor 1 и Factor 3 (рис. VII.44). В диалоговом окне Factor Analysis Results: на вкладке Loadings щелкнем кнопкойPlot of loadings, 3D. Результатом будет трехмерный график нагрузок (рис. VII.45).
Рис. VII.42. Диалоговое окно Select two factors for the plot
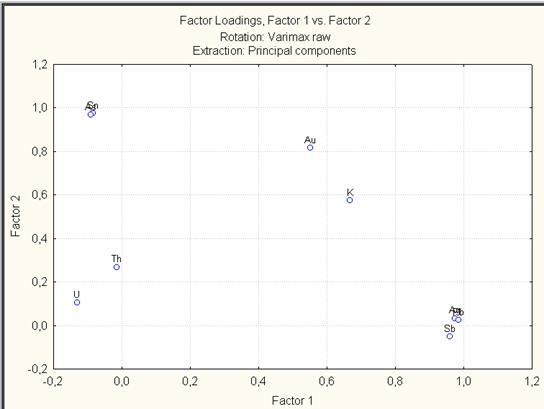
Рис. VII.43. График нагрузок Plot of loadings, 2D для факторов 1 и 2
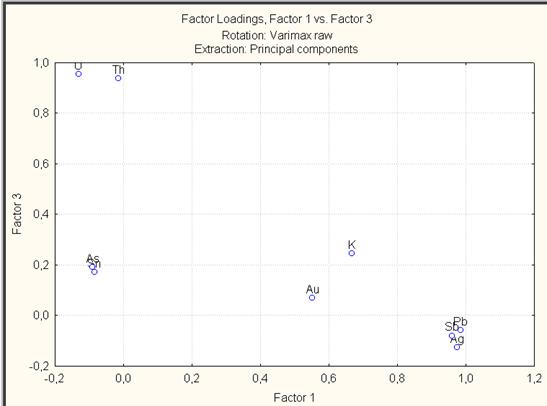
Рис. VII.44. График нагрузок Plot of loadings, 2D для факторов 1 и 3
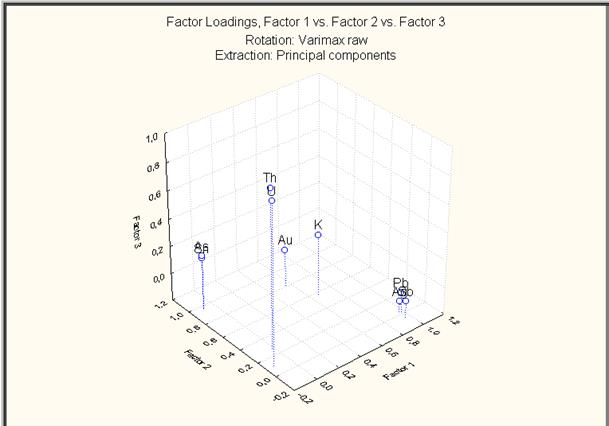
Рис. VII.45. График нагрузок Plot of loadings, 3D для факторов 1, 2 и 3
Графики (рис. VII.43 – VII.45) нагрузки для каждой переменной и отлично иллюстрируют корреляционную матрицу, к примеру, по рис. VII.43 видно, что ассоциированы мышьяк (As) и олово (Sn); серебро (Ag), сурьма (Sb) и свинец (Pb); уран (U) и торий (Th). Фактор 2 – фактор с высокими нагрузками на Au – «рудный» и фактор 3 связан с околорудным метасоматозом. Обратите внимание на нагрузки факторов, чтобы выяснить, в какой мере эта закономерность характеризует изучаемый объект.
Щелкнуть в диалоговом окне Factor Analysis Results: на вкладке Explained variance кнопкойReproduced/residual corrs. (рис. VII.46), чтобы получить две остаточной – корреляции и матрицы корреляции (рис. VII.47).
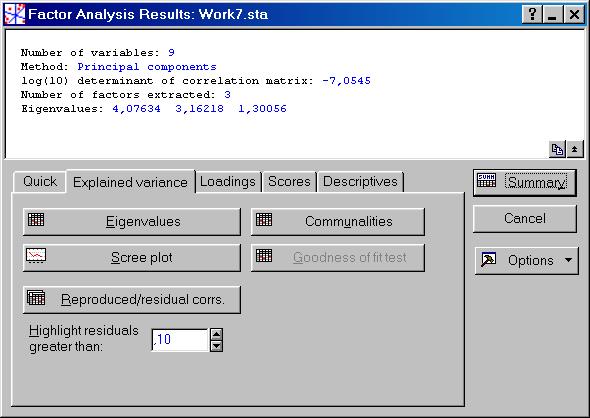
Рис. VII.46. Диалоговое окно Factor Analysis Results: вкладке Explained
Таблица остаточных корреляций может интерпретироваться как «количество» корреляции, которое не может быть растолковано ответом с тремя факторами. Диагональные элементы в матрице содержат стандартное отклонение, которое есть равным квадратному корню из единицы минус соответствующие общности для двух факторов (общности переменной – отличие, которую возможно растолковывать соответствующим числом факторов). В случае, если разглядеть шепетильно эту матрицу, возможно видеть, что нет практически никаких остаточных корреляций, каковые являются громадными, чем 0,1, либо меньше чем –0,1. Добавить к этому факт, что первые три фактора растолковывали практически 95 % полной отличия (см. совокупный % Eigenvalues продемонстрированный в таблицеEigenvalues на рис. VII.34). Низкие общности для одной либо двух переменных (из всех в анализе) смогут показывать, что эти переменные не хорошо разъясняются соответствующей моделью фактора.
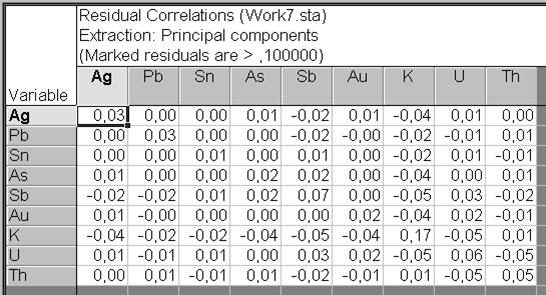
Рис. VII.47. Таблица остаточных корреляций
Щелкнуть в диалоговом окне Factor Analysis Results: на вкладке Explained variance кнопкойCommunalities (рис. VII.46), для получения таблицы общностей для текущего ответа, другими словами текущего числа факторов (рис. VII.48).
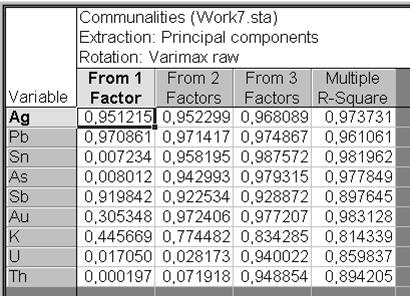
Рис. VII.48. Таблица общностей
Щелкнуть в диалогом окне Factor Analysis Results: на вкладке Scores кнопкой Factor scores coefficients, для получения таблицы со значениями каждого фактора элементов (рис. VII.49). Эти коэффициенты воображают веса, каковые употребляются в то время, когда вычисляется зависимость фактора от переменных.
Щелкнуть в диалогом окне Factor Analysis Results: на вкладке Scores кнопкой Factor scores, для получения таблицы со значениями каждого фактора в точках наблюдения (рис. VII.50). Обратите внимание, в каких точках наблюдения значения рудного фактора громаднейшие: 4 – 6, 11, 17, 19, 21, 24. Фактор околорудного метасоматоза – 1, 4, 8, 13 – 15, 20, 21, 24, 26 – 28, 31, 33 – 34, 36. Неспециализированные: 4, 21, 24.
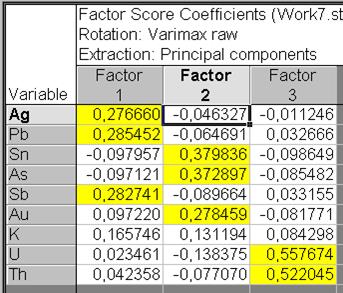
Рис. VII.49. Таблица Factor scores coefficients
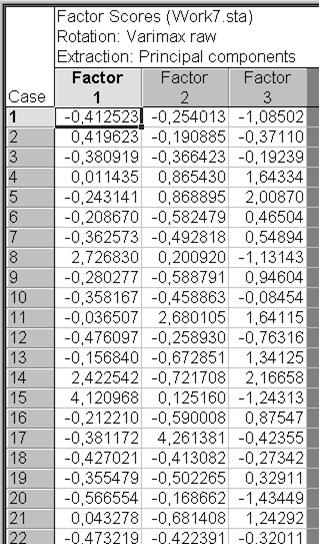
Рис. VII.50. Таблица Factor scores
В таблице Factor scores выделить «фактор» и» – 2 рудный фактор околорудного метасоматоза – 3. После этого выбрать процедуру графического анализа в контекстном меню Graphs of Block Data\Line Plots: Entire Columns. На взятом графике указать места, где максимально показаны факторы рудного метасоматоза (рис. VII.51).
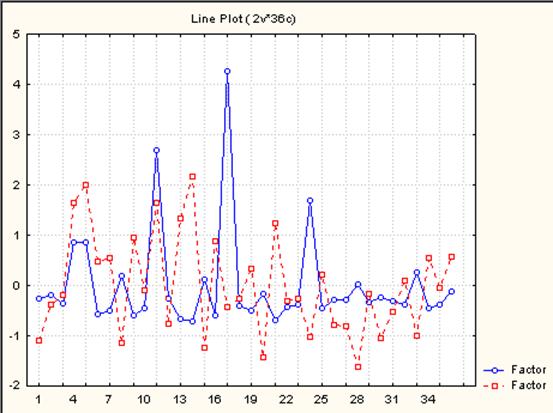
Рис. VII.51. Итог исполнения процедуры в контекстном менюGraphs of Block Data\Line Plots: Entire Columns.
8. Сделать окончательные выводы о химических прогнозной значимости и ассоциациях элементов объекта.
Сравнить результаты корреляционного, кластерного и факторного анализов, их отличия, которые связаны с возможностями каждого анализа, и неспециализированные черты, разрешающие дать взвешенное заключение о закономерных связях между изучаемыми показателями.
ОБЛАСТЬ ПРИМЕНЕНИЯ МНОГОМЕРНЫХ СТАТИСТИЧЕСКИХ МОДЕЛЕЙ В ГЕОЛОГИИ
Возможности применения многомерных статистических моделей для изучения взаимозависимостей комплексов самых разных геологических показателей фактически не ограничены для любой отрасли геологии. В палеонтологии они употребляются для статистического описания морфологических показателей ископаемых сопоставления и форм организмов их групп с литолого-фациальными разрезами осадочных пород, с целью оценки достоверности их стратиграфического положения (либо установления групп руководящих ископаемых). Корреляционные способы парагенетического анализа химических минералов и элементов находят широкое использование в минералогии и геохимии. Разные способы многомерного описания самых разных физических особенностей, химического и минерального состава осадочных и магматических пород употребляются в петрографии и литологии для разделения их по фациальным либо формационным показателям либо для оценок их возможностей на обнаружение самых разных нужных ископаемых. Из года в год все шире употребляются способы «распознавания образов» рудоносных территорий либо месторождении нужных ископаемых, основанные на статистических описаниях сочетаний благоприятных элементов геологического строения, воздействующих на концентрации нужных ископаемых. На данный момент методы «распознавания образов», применяющие самые разные статистические, логические и эвристические многомерные модели, реализуются в человеко-машинных информационно-прогнозирующих совокупностях, на шедших широкое использование в геологоразведочной отрасли.
Многомерные статистические описания связей геологических переменных с последующими оценками степени их взаимозависимостей употребляются в геологической практике с целью идентификации (отождествления), дискриминации (разделения), классификации (группирования) изучаемых объектов либо в отыскивании самые информативных комбинаций показателей для ответа прогнозных задач.
Задачи идентификации геологических объектов, к примеру, оценки коллекторских особенностей либо газоносности пород по совокупности скважинно-геофизических черт, в большинстве случаев выполняются посредством моделей множественной регрессии.
В целях дискриминации геологических объектов на два заблаговременно заданных класса, к примеру, разделение кимберлитовых пород на алмазоносный и неалмазоносный типы, согласно данным их силикатных анализов возможно использована модель линейной дискриминантной функции.
Классификация геологических объектов, к примеру, иерархическое группирование парагенетических ассоциаций элементов метасоматически поменянных пород либо руд согласно данным их полных химических анализов производится посредством кластер-анализа, вторых способов многомерного корреляционного анализа либо способа факторного анализа.
Конечной целью большинства многомерных статистических способов есть предсказание (прогнозирование) тех либо иных особенностей изучаемых геологических объектов.
Прогнозирование особенностей геологических объектов, значительно чаще обнаружение возможностей их рудоносности либо оценка возможных масштабов оруденения проводится посредством методов «распознавания образов».
В зависимости от характера данных и целей геологических изучений для составления этих методов употребляются самые разные многомерные модели. Наряду с этим, в большинстве случаев, появляется неприятность поиска наиболее сокращения размерности и информативных сочетаний признаков их пространства, что достигается посредством способа основных компонент, R-способа факторного анализа или других логических и эвристических способов.
Возможности применения многомерных статистических моделей для целей ответа геологических задач изучены на данный момент далеко не абсолютно и без сомнений имеют громадное будущее.
ЛАБОРАТОРНАЯ РАБОТА № VIII. МНОГОМЕРНЫЕ СТАТИСТИЧЕСКИЕ МОДЕЛИ. ЗАДАЧИ РАСПОЗНАВАНИЯ ОБРАЗОВ В ГЕОЛОГИИ
Многие прогнозные и интерпретационные задачи решаются в практической геологии методом сопоставления комплекса показателей изучаемого объекта с комплексом тех же показателей эталонного объекта. Совокупность аналогичных способов, основанных на принципе аналогии, стала называться способов распознавания образов.
Модели распознавания образов геологических объектов очень разнообразны. При ответе конкретных геологических задач их выбор зависит от природы геологических объектов, числа, полноты описания эталонных объектов, информативности и типов их показателей. В зависимости от типов исходных показателей выделяют две группы моделей: дискретные и постоянные.
Дискретные модели используются в тех случаях, в то время, когда измеряемые показатели рассматриваются как свободные либо частично зависимые детерминированные размеры.
Постоянные модели употребляются для распознавания образов таких объектов, измеряемые показатели которых смогут рассматриваться как случайные размеры и поддаются статистическому описанию многомерными функциями плотностей возможности.
В качестве параметров оптимальности распознавания употребляются решающие правила, определяющие пороговые значения решающих функций. Они смогут определяться статистическими, логическими либо эвристическими * способами.
При применении любых методов распознавания направляться стремиться к построениям решающих функций максимально несложных видов, потому, что они легче поддаются реализации и снабжают более устойчивые ответы, в особенности при малых выборках обучения.
Линейная дискриминантная функция для трех переменных имеет форму
. (VIII.1)
Коэффициенты a1, a2 и a3 находятся из совокупности уравнений
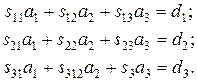(VIII.2)
Величины d1, d2 и d3 представляют собой разности оценок средних значений показателей по выборкам A и B.
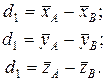(VIII.3)
В случае, если обозначить номер строчка как i, а столбца как j, то величины sij возможно записать в форме матрицы:
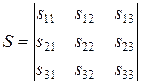. (VIII.4)
Значения sij соответствуют элементам ковариационной матрицы показателей X, Y, Z и вычисляются, как суммы квадратов отклонений либо суммы смешанных произведений отклонений:
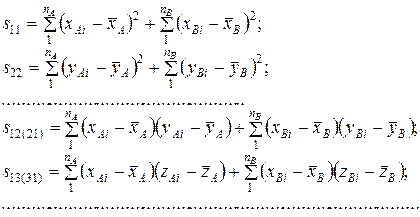
Вышеприведенные выражения для удобства расчетов смогут быть заменены на эквивалентные выражения для сумм квадратов вида
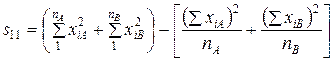, (VIII.5)
и для сумм смешанных произведения вида
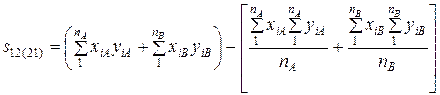, (VIII.6)
где nA и nB – количество выборки для объекта A и B.
По окончании вычисления коэффициентов a1, a2 и a3, нужно вычислить значение функции D0, довольно которого возможно сделать вывод о принадлежности нового малоизвестного объекта к тому либо иному классу (свите)
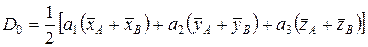. (VIII.6)
В Excel для вычисления ковариации употребляется процедура Ковариация. Процедура дает возможность приобрести ковариационную матрицу, содержащую коэффициенты ковариации между разными параметрами.
Для реализации процедуры нужно:
- выполнить команду Сервис/Анализ данных;
- в показавшемся перечне Инструменты анализа выбрать строчок Ковариация и надавить кнопку OK;
- в показавшемся диалоговом окне указать Входной промежуток, другими словами ввести ссылку на ячейки, которые содержат разбираемые эти. Для этого направляться навести указатель мыши на левую верхнюю ячейку данных, надавить левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к правой нижней ячейке, содержащей разбираемые эти, после этого отпустить левую кнопку мыши. Входной промежуток обязан содержать как минимум несколько столбцов.
- в разделе Группировкапереключатель установить в соответствии с введенными данными;
- указать выходной диапазон, другими словами ввести ссылку на ячейки, в каковые будут выведены результаты анализа. Для этого направляться поставить флажок в левое поле Выходной промежуток (навести указатель мыши и щелкнуть левой кнопкой), потом навести указатель мыши на правое поле ввода Выходной промежуток и щелкнуть левой кнопкой мыши, после этого указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши. Размер выходного диапазона будет выяснен машинально, и на экран будет выведено сообщение при вероятного наложения выходного диапазона на данные.