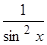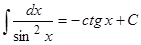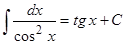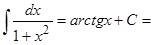Пример 7. Изучить и выстроить схематичный график функции .
Применяя схему изучения графика функции посредством производных, отыщем:
1. .
2. Отыщем точки пересечения графика функции с координатными осями
,т.е. –точка пересечения с осью абсцисс;
, т.е. –точка пересечения с осью ординат.
3. Вычислим – функция неспециализированного вида.
4. Функция непериодическая.
5. Отыщем первую производную функции , которая существует на всей числовой оси, следовательно, отыщем критические точки, решая уравнение . Отложим отысканную точку на числовой оси и определим символ первой производной на каждом промежутке
– +
–1
Из рисунка видно, что и . Так как при пе-реходе слева направо через точку первая производная меняет собственный символ с “–” на “+”, то в данной точке отмечается минимум. Вычислим значение функции в минимуме .
6. Отыщем вторую производную функции , которая существует на всей числовой оси, следовательно, отыщем точки, странные на перегиб, решая уравнение . Отложим отысканную точку на числовой оси и определим символ второй производной на каждом промежутке
– +
–2
Из рисунка видно, что и . Так как при переходе слева направо через точку вторая производная меняет собственный символ, то в данной точке отмечается точка перегиба. Вычислим значение функ-ции в точке перегиба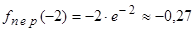 
.
7. Отыщем асимптоты графика функции, для чего вычислим угловой коэффициент прямой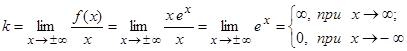 
. Так, при асимптот нет, а при вероятна горизонтальная асимптота. Вычислим параметр 
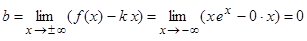. Следовательно, график заданной функции имеет горизонтальную асимптоту .
8. Выстроим сводную таблицу
| Промежуток | |||||
– точка пересечения с координатными осями.
– горизонтальная асимптота.
9. Выстроим схематичный график функции, выбрав по координатным осям различные масштабы измерения
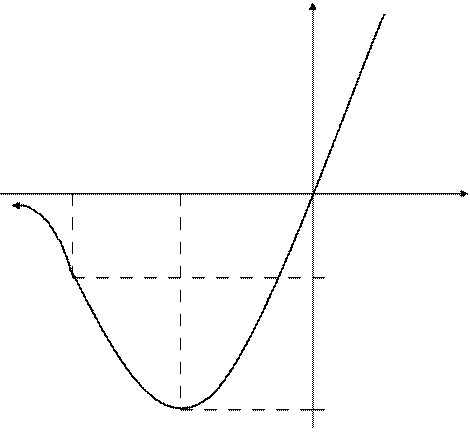
-2 -1
— 0.27
— 0.37
“Неизвестный его свойства и интеграл”
1. Первообразная. Неизвестный интеграл.
При ответе многих практических задач таких, как вычисление длин линий, площадей, отыскание траекторий перемещения и других, вводится понятие интегрирования.
О1. Первообразнойфункции именуется такая функция , первая производная от которой равна заданной функции, т.е. .
Т1. (о существовании первообразной) В случае, если функция постоянна на сегменте , то на этом промежутке существует первообразная данной функции.
Т2. В случае, если – первообразная функции , то функция ( – произвольная постоянная) кроме этого есть первообразной функции .
Т3. В случае, если и первообразные функции , то они отличаются друг от друга на постоянную величину.
Пример 1. Пускай дана функция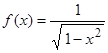 
. Отыскать первообразную данной функции. При наличия двух первообразных продемонстрировать, что они отличаются на постоянную величину.
Для функции существуют две первообразные и . Их разность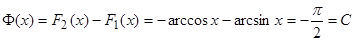 
.
О2. Совокупность всех первообразных функции именуется неизвестным интегралом и обозначается , где – переменная интегрирования, – подинтегральная функция, – подинтегральное выражение.
На основании Т2 и Т3 возможно записать, что .
О3. Отыскание всех первообразных именуется неизвестным интегрированием.
Узнаем геометрический суть неизвестного интеграла. Пускай дана функция и требуется отыскать такую кривую , для которой в каждой ее точке тангенс угла наклона касательной равен значению функции в данной точке. Таковой линией будет кривая, для которой . Так, неизвестный интеграл определяет все кривые, у которых тангенс угла наклона в каждой ее точке сходится со значением функции .
2. Свойства неизвестного интеграла.
1. Производная от неизвестного интеграла равна подынтегральной функции .
2. Дифференциал неизвестного интеграла равен подынтегральному выражению .
3. В случае, если подынтегральное выражение есть дифференциалом некоей функции , то неизвестный интеграл равен .
4. Неизвестный интеграл от линейной комбинации функций равен той же самой линейной комбинации неизвестных интегралов от этих функций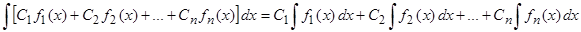 
.
Частные случаи:
а) неизвестный интеграл от суммы (разности) функций равен сумме (разности) неизвестных интегралов от этих функций
.
б) постоянный множитель возможно выносить за символ неизвестного интеграла .
5. Формула неизвестного интеграла не зависит от обозначения переменной интегрирования .
3. Таблица главных неизвестных интегралов.
| Подынтегральная функция | Неизвестный интеграл | Частные случаи |
| Степенная |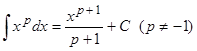 
|
 
|
|
||
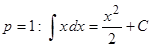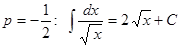
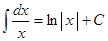
| Показательная |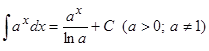 
|
|
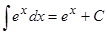
| Тригонометрические
|
|
|
 
|
   
|
|
 
|
 
|
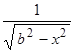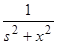
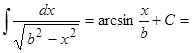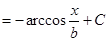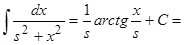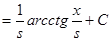
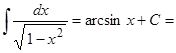
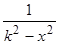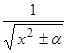
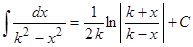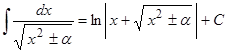
Пример 3. Применяя таблицу неизвестных интегралов, вычислить интегралы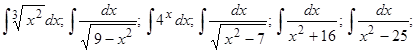 
(самостоятельно).
“Способы интегрирования”
1. Способ тождественных преобразований подынтегральной функции.
Этот способ основан на применении несложных приемов, алгебраических и тригонометрических формул, особенностей подынтегральной функции, разложения полиномов на простые множители и особенностей неизвестного интеграла. Разглядим данный способ на конкретных примерах.
1. Почленное деление числителя дроби на ее знаменатель 
.
Пример 1. Отыскать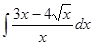 
.
Выполним в подынтегральной функции почленное деление числителя дроби на ее знаменатель и воспользуемся свойством линейности неизвестного интеграла
.
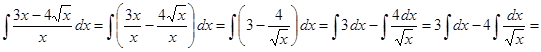2. Применение противоположных арифметических операций (к примеру, сложение-вычитание).
Пример 2. Отыскать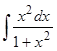 
.
Анализ подынтегральной функции говорит о том, что в числитель дроби нужно добавить и вычесть 1 (наряду с этим подынтегральная функция не изменится), а после этого воспользоваться первым приемом (почленное деление числителя дроби на ее знаменатель)
.
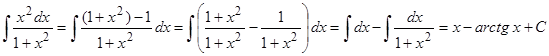3. Применение алгебраических и тригонометрических формул, к примеру,
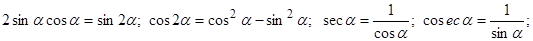
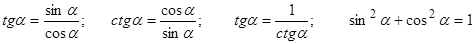
и других формул.
Пример 3. Отыскать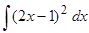 
.
Воспользуемся формулой квадрата разности
.
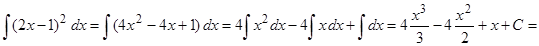
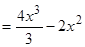Пример 4. Отыскать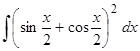 
.
Поступим подобно примеру 3
.
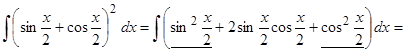
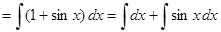4. Применение особенностей функций, к примеру,
.
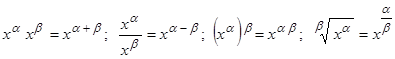Пример 5. Вычислить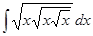 
.
.
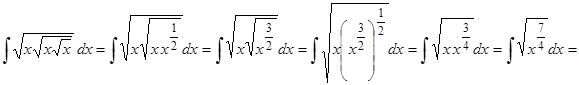
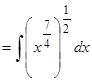
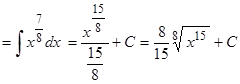Пример 6. Вычислить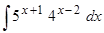 
.
.
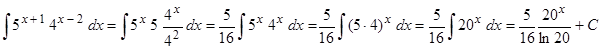5. Применение разложения многочленов на простые множители, к примеру, , где и корни уравнения .
Пример 7. Отыскать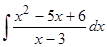 
.
По теореме Виета уравнение имеет корни и , следовательно, разложение квадратичного многочлена на простые множители имеет форму: . Подставим полученное выражение в подынтегральную функцию, возьмём
.
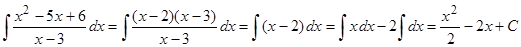2. Способ замены переменной интегрирования.
Этот способ основан на формуле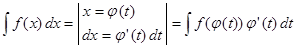 
.
Способ замены переменной интегрированияприменяется в двух случаях:
а) В случае, если довод функции отличается от несложного довода , то данный сложный довод принимается в качестве новой переменной интегрирования .
Пример 8. Вычислить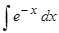 
.
Так как показатель степени экспоненты отличается от несложного довода , то данный показатель степени принимаем в качестве новой переменной интегрирования, т.е.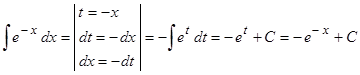 
.
З4. По окончании нахождения первообразной с новой переменной интегрирования нужно непременно возвратиться к ветхой переменной интегрирования.
Пример 9. Вычислить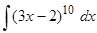 
.
Выражение, стоящее в круглых скобках, есть доводом степенной функции и отличается от несложного довода , исходя из этого принимаем его в качестве новой переменной интегрирования, т.е.
.
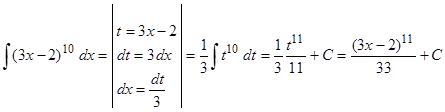Пример 10. Вычислить .
Выражение, стоящее в круглых скобках, есть доводом функции синус и отличается от несложного довода , исходя из этого принимаем его в качестве новой переменной интегрирования, т.е.
.
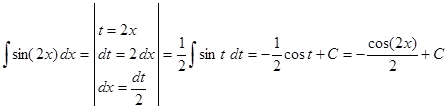б) В случае, если элементарная функция, содержащаяся в подынтегральном выражении, имеет несложной довод и в качестве множителя при присутствует первая производная данной функции, то в качестве новой переменной интегрирования принимается эта элементарная функция.
Пример 11. Отыскать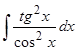 
.
В подынтегральном выражении содержится элементарная функция и в качестве множителя при присутствует ее первая производная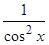 
, следовательно, в качестве новой переменной интегрирования принимаем :
.
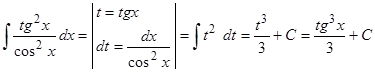Пример 12. Отыскать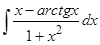 
.
Этот пример объединяет первый способ с способом замены переменной интегрирования. Выполним почленное деление числителя дроби на ее знаменатель и разобьем интеграл на два интеграла, для которых используются два случая замены переменной интегрирования
.
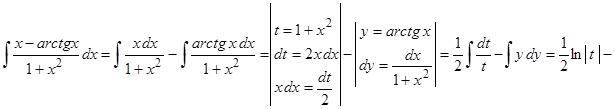
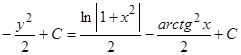З5. Умение отыскивать подходящую замену вырабатывается в ходе многократных упражнений, но возможно указать последовательность случаев, в то время, когда возможно сходу заметить нужную замену переменной интегрирования при анализе подынтегрального выражения, к примеру,
.
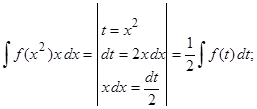
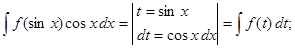
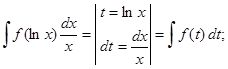
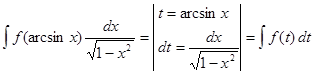Из продемонстрированных примеров видно, что умение отлично интегрировать зависит от хорошего знания таблицы производных от элементарных функций.
3. Способ интегрирования по частям.
Интегрирование по частям основано на применении формулы дифференциала от произведения двух функций , откуда находим, что произведение . Так, для неизвестного интеграла формула интегрирования по частям имеет форму:
.
Чтобы знать, какую из функций принимать за (все другое в
подынтегральном выражении принимается за ), разглядим самый час-
то видящиеся случаи:
1. 
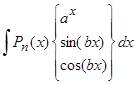, где 
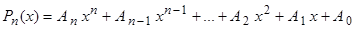– многочлен порядка .
В этом случае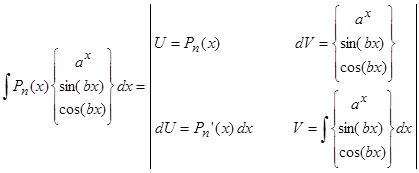 
.
З6. Для нахождения функции применяют определение дифференциала функции. При вычислении функции интегрируют выражение , наряду с этим постоянная интегрирования надеется равной нулю ( ). По окончании исполнения этих действий используют формулу интегрирования по частям.
Пример 13. Вычислить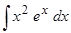 
.
Применим способ интегрирования по частям
.
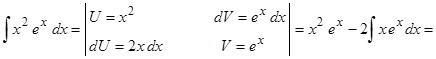
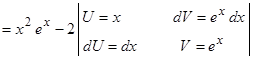
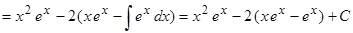З7. Из приведенного примера видно, что при необходимости способ интегрирования по частям используется повторно.
2. Для интегралов вида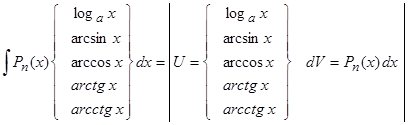 
.
Пример 14. Вычислить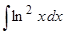 
.
Действуя в соответствии с методике, возьмём
.
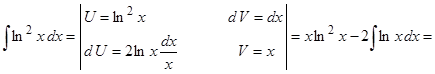
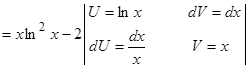
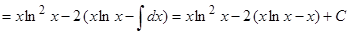3. Для интегралов вида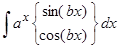 
, каковые именуются возвратными, на первом шаге интегрирования безразлично, какую из функций (показательную либо тригонометрическую 
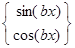) принимать в качестве функции . Но на втором шаге в качестве функции нужно непременно принимать ту из функций (показательную либо тригонометрическую 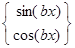), которая была принята на первом шаге, в другом случае интеграл возвращается к собственному исходному виду при отсутствии проинтегрированной части.
Пример 15. Отыскать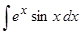 
.
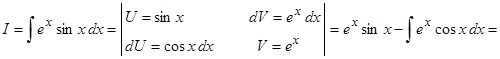(в случае, если на данный момент в качестве функции выбрать экспоненту, то интеграл возвратится к собственному начальному виду при отсутствии проинтегрированной части; убедитесь в этом самостоятельно)
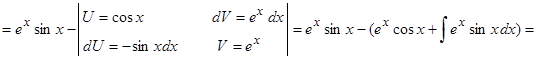
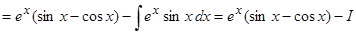. Решим полученное уравнение относительно буквы : ; . Из этого находим, что 
.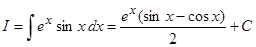