ПО ИНЖЕНЕРНОЙ ГРАФИКЕ
Издательство МГТУ им. Н.Э. Баумана
Г.
Рабочая тетрадь по инженерной графике / Сост. Золотова Г.П., Момджи Т.Д.,
Новик Н.В.: -М.: Изд-во МГТУ им. Н.Э. Баумана, 2008, — с., ил.
Рабочая тетрадь содержит материалы для практических занятий по курсу “Инженерная графика”, и задания для независимого ответа.
В тетрадь входят как задачи по начертательной геометрии, так и по черчению, которые связаны с построением изображений по ГОСТ 2.305-68 (Изображения – виды, разрезы, сечения).
Графическое ответ задач направляться осуществлять конкретно в рабочей тетради посредством чертежных инструментов. Наряду с этим линии связи и вспомогательные построения проводятся целыми узкими линиями, а конечный итог обводится целыми толстыми главными линиями по ГОСТ 2.303-68.
Буквенные и цифровые обозначения наносятся в соответствии с принятой символике и выполняются чертёжным шрифтом по ГОСТ 2.304-81.
Задачи, отмеченные знаком *, в административном порядке должны быть решены в 3D-пространстве в совокупности Автокад на лабораторных работах.
Для студентов всех преподавателей и специальностей, трудящихся в области инженерной графики.
ПЕРЕЧЕНЬ ЛИТЕРАТУРЫ
1. С.А. Фролов Начертательная геометрия. М.: Машиностроение, 1983.
2. С.А. Фролов. Сборник задач по начертательной геометрии: Учебное пособие для студентов втузов. — М.: Машиностроение, 1980. –142 с. , ил.
3. Арустамов Х.А. Сборник задач по начертательной геометрии с ответом типовых задач. Учебное пособие для студентов втузов. — М.: Машиностроение, 1980.
2. ЕСКД. Сборник стандартов. М.: Изд-во стандартов,1991.
ОГЛАВЛЕНИЕ
Обозначения и знаки…………………………………………………………………………4
1. Способ проекций. Центральные, параллельные и ортогональные проекции………………6
2. Проекции точки………………………………………………………………………………..7
3. Проекции прямой линии. Положение прямой относительно плоскостей проекций.
Точка на прямой. Определение настоящей величины отрезка углов и прямой
его наклона к плоскостям проекций. Обоюдное положение прямых.
Проецирование прямого угла ……………………………………………………………….8
4. Плоскость. Точки и прямые линии, расположенные в плоскости………………………..11
5. Обоюдное положение двух плоскостей, плоскости и прямой линии (параллельность,
пересечение, перпендикулярность)…………………………………………………………13
6. Методы преобразования ортогональных проекций………… ……………………………18
7. Метрические задачи. Определение величин и расстояний углов………………………….20
8. Поверхности. линия и Точка на поверхности……………………………………….……..24
9. Пересечение поверхностей с прямой и плоскостью. Касательные плоскости. ………….26
10. Обоюдное пересечение поверхностей………………………………………………………30
11. Проецирование геометрических моделей и тел…………………………………………..40
12. Построение изображений. Виды, разрезы, сечения………………………………………43
Обозначения и знаки
1. Точки обозначаются прописными буквами латинского алфавита либо арабскими цифрами:
А, В, С, D,…, L, M, N…
1, 2, 3, 4,…,12, 13, 14 …
2. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:
a, b, c, d, …, l, m, n…
3. Линии уровня обозначаются:
h — горизонталь,
v — фронталь,
w — профильная прямая.
4. Поверхности обозначаются строчными буквами греческого алфавита:
?, ?, ?, ?, …, ?, ?, ?,…
5. Углы обозначаются строчными буквами греческого алфавита с добавлением индекса «градус»:
??, ??, ??, …, ??, ??, ??,…
6. Плоскости проекций обозначаются:
— горизонтальная;
— фронтальная;
— профильная;
, ,… — дополнительные плоскости проекций.
7. Оси проекций обозначаются строчными буквами латинского алфавита x, y, z ;
начало координат прописной буквой O.
8. Последовательность точек, линий либо поверхностей отмечается подстрочными индексами:
.
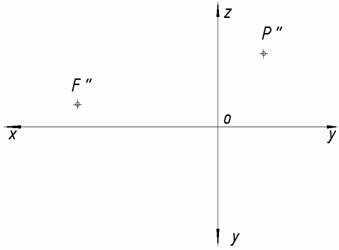
9. Проекции точек, линий, поверхностей, любой фигуры на плоскостях проекций обозначаются теми же буквами (либо цифрами), что и оригинал, с добавлением верхнего индекса. Верхний индекс соответствует плоскости проекций, на которой они взяты, к примеру:
(горизонтальные проекции) — A?, B?, 1?, 2?,… a?, b?,… ??, ??,…;
(фронтальные проекции) — A?, B?, 1?, 2?,… a?, b?,… ??, ??,…;
(профильные проекции) — A??, B??, 1??, 2??,… a??, b??,… ???, ???,…;
(дополнительные проекции) —A???, B???, 1???, 2???,… a???, b???,… ????, ????,…
10. Следы плоскостей обозначаются:
-горизонтальный след плоскости ?;
— фронтальный след плоскости ?;
— профильный след плоскости ?.
11. Расстояние между фигурами пространства обозначаются двумя вертикальными линиями | | .К примеру:
|АВ| — расстояние между точками А и В (протяженность отрезка АВ);
|Ab| — расстояние от точки А до линии b;
|A?| — расстояние от точки А до поверхности ?;
|bc| — расстояние между линиями b и c;
|??| — расстояние между поверхностями ? и ?.
12. Следующие знаки обозначают:
?- совпадение (тождественность) двух геометрических элементов либо их проекций, к примеру, А?В,a??b?;
|| — параллельность;
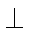 — перпендикулярность;
— перпендикулярность;
— скрещиваются.
| 3. Проекции прямой линии. Положение прямой относительно плоскостей проекций. Точка на прямой. Определение настоящей величины отрезка углов и прямой наклона к плоскостям проекций. Обоюдное положение прямых. Проецирование прямого угла. | |
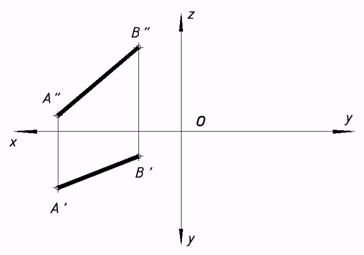
| 7*. Выстроить проекции прямых, симметричных заданной прямой AB относительно: -плоскости проекций p1 (прямая CD); -плоскости проекций p2 (прямая KL). Назвать октанты, в которых находятся прямые: AB — в……октанте. CD — в……октанте. KL — в…… октанте. |
|
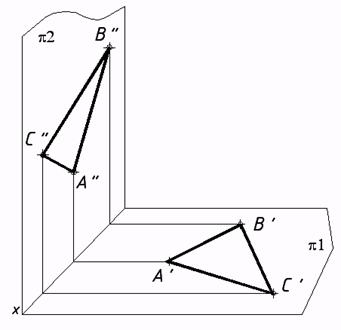
| 8*. Выстроить проекции треугольника ABC по координатам его вершин A(25,5,20), B(25,20,0), C(5,20,20). Выяснить длины и углы наклона сторон треугольника к плоскостям проекций. | 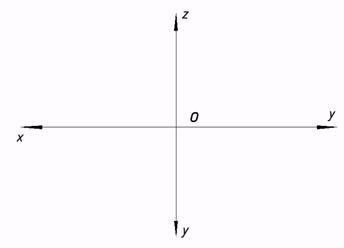
|
9*. Через точку B совершить прямые: h – параллельно p1; f – параллельно p2; w – параллельно p3; d – неспециализированного положения. 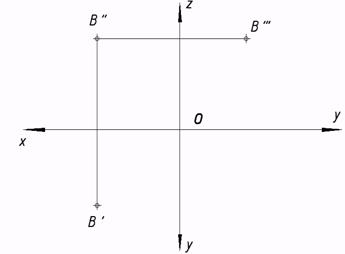
|
10.* Выстроить недостающие проекции точки C, принадлежащей отрезку AB. 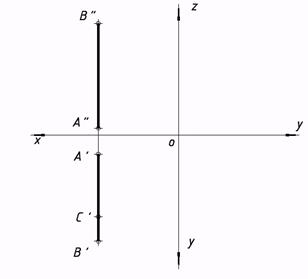
|
15*. Пересечь прямые AB и CD третьей прямой, перпендикулярной к ним, т.е. отыскать малейшее расстояние между скрещивающимися прямыми AB и CD. 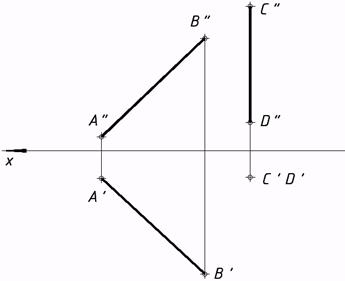
|
16*. Выяснить натуральную величину расстояний от точки С до заданных прямых. 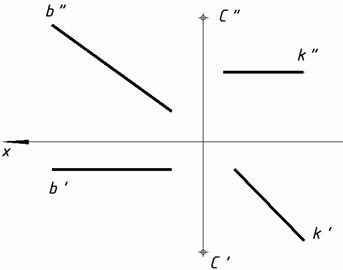
|
|
17*. Выстроить прямоугольник ABCD со стороной BC=1,5АВ на прямой m, которая параллельна плоскости проекций p2. Выяснить углы наклона стороны АВ к плоскостям проекций. 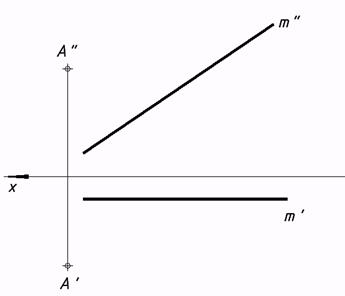
|
18*. Обнаружить прямой m точку, удаленную от точки С на 35 мм. Какие конкретно вероятны случаи? 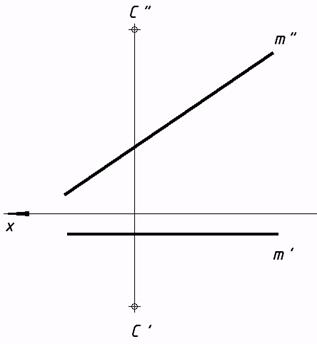
|
Плоскость. Точки и прямые линии, расположенные в плоскости.
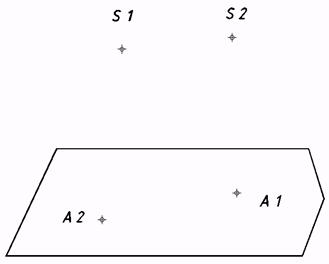
19*. Совершить через точку А плоскость ?||?1 на расстоянии 25мм., через точку В плоскость ?||?2 на расстоянии 20мм., через точку С плоскость ?||?3 на расстоянии 15мм. Выстроить плоскость неспециализированного положения в виде треугольника АВС. Выстроить недостающие проекции точек. 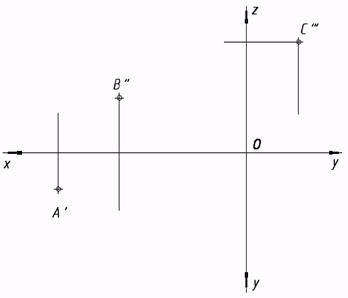
|
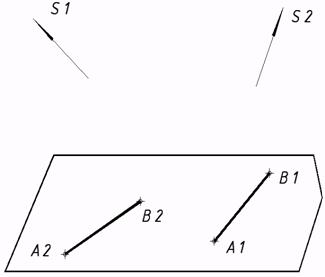
20*. Совершить через прямую AB две плоскости: a^p1; b^p2. Выяснить углы наклона этих плоскостей к плоскостям проекций p1 и p2. Плоскости задать следами. 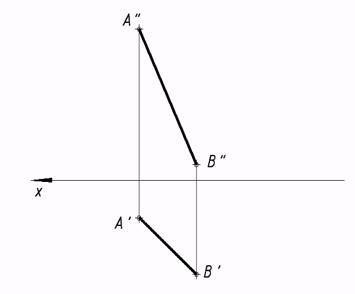
|
21*. Выстроить следы плоскости, заданной параллельными прямыми AB и CD. 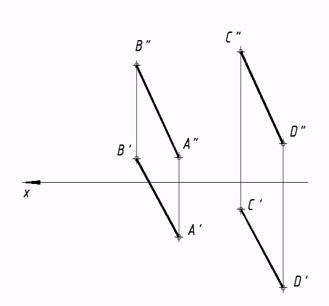
|
22*. В плоскости, заданной точками А, B, C, совершить: через точку A – горизонталь; через точку C – фронталь; через точку B — линии громаднейшего наклона к плоскостям проекций p1и p2 . 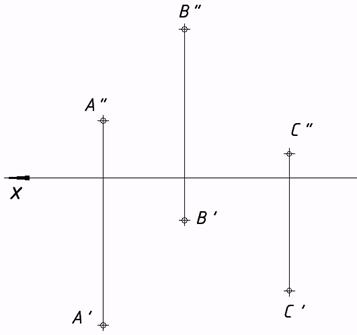
|
23*. Выстроить нехватающую проекцию отрезка AB, лежащего в плоскости a. Проверить, в собственности ли отрезок CD заданной плоскости ? 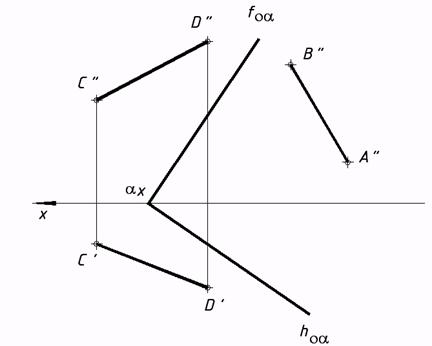 24*. Выяснить углы наклона плоскости треугольника к плоскостям проекций p1 и p2. 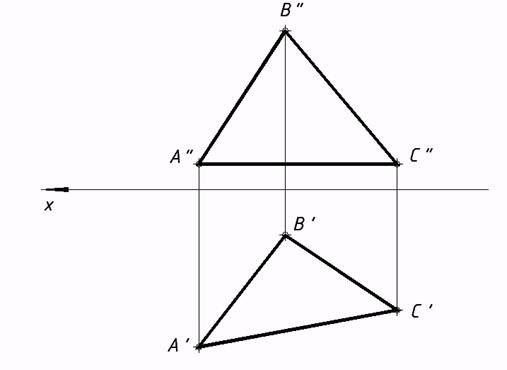
|
|
5. Обоюдное положение двух плоскостей, (параллельность, пересечение, 25*. Проверить, параллельны ли заданные плоскости? Через точку С совершить плоскость параллельно плоскости ?. Плоскость задать как следами, так и пересекающимися прямыми. 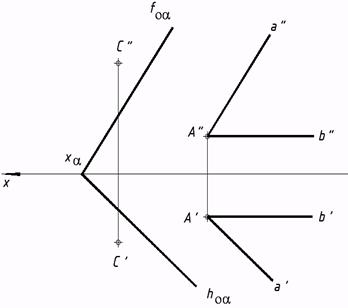 27*. Отыскать линии пересечения плоскостей, заданных следами (рис. a, b, с). 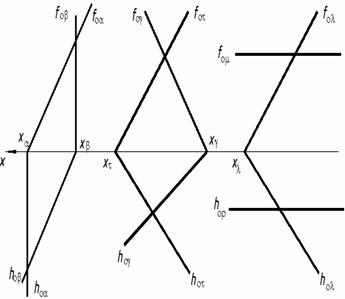 а) b) с) |
плоскости и прямой линии перпендикулярность). 26*. Проверить, параллельна ли заданная прямая АВ плоскости ?? Через точку D совершить любую прямую параллельно заданной плоскости. 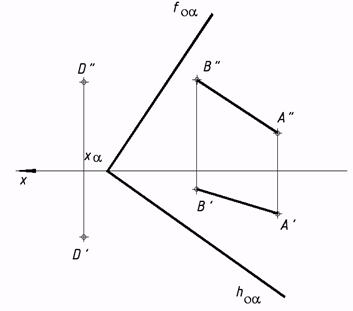 28*. Выстроить линию пересечения двух плоскостей и выяснить их видимость 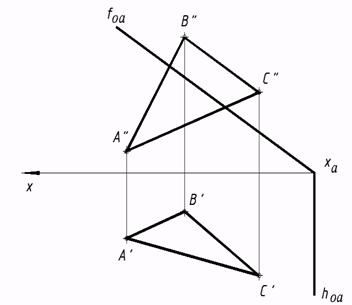
|
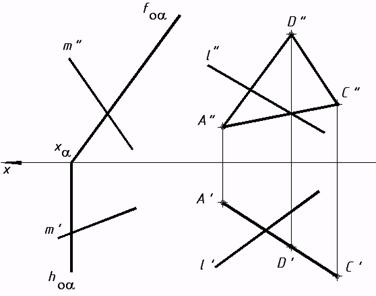
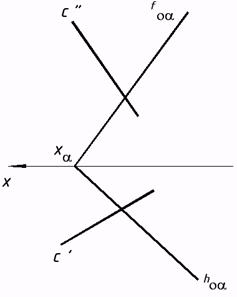
a) b) c) 30*. Отыскать линию пересечения заданных плоскостей.
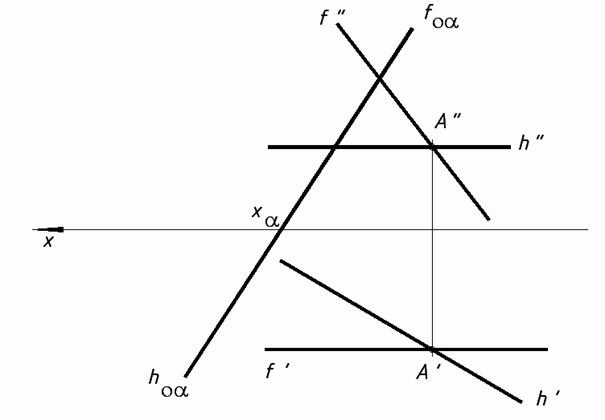
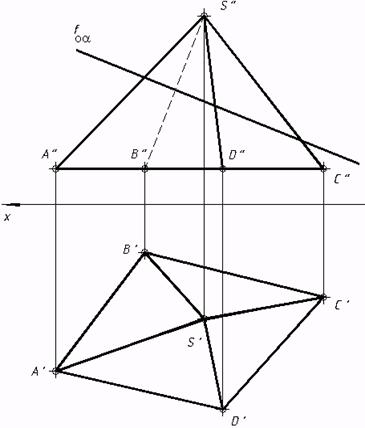
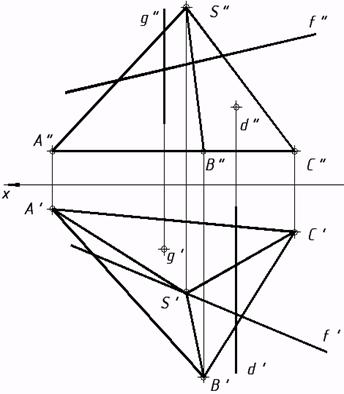
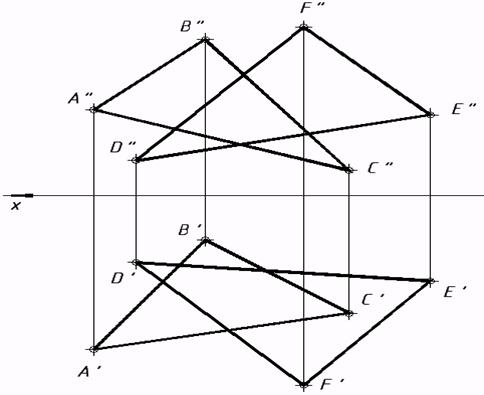
34*. Выяснить малейшее расстояние от точки М до заданных плоскостей. 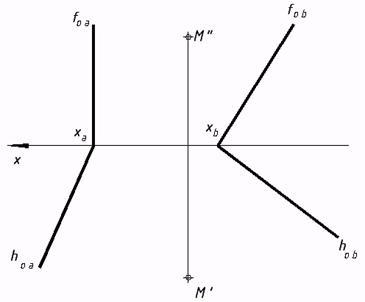 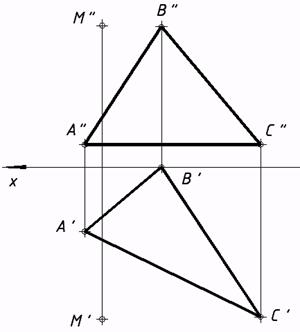 35*. Из точки A восставить перпендикуляр к плоскости a, заданной треугольником. На этом перпендикуляре отыскать точку, удаленную от плоскости a на расстояние 30 мм, и через нее совершить плоскость buu a. 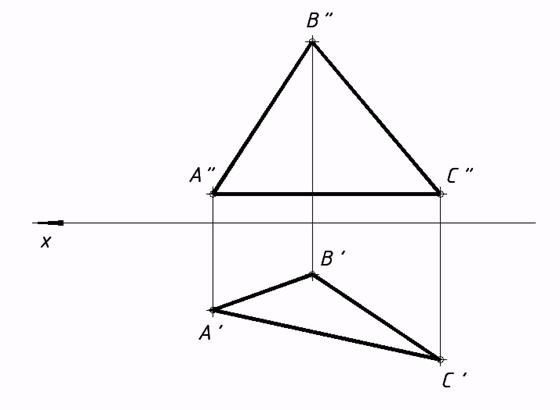 36*. Выяснить расстояние от точки А до прямой n. 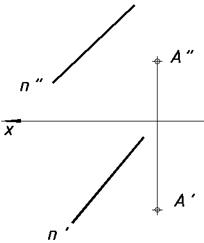 37*. Выстроить нехватающую проекцию прямой d, в случае, если как мы знаем, что она перпендикулярна прямой m. 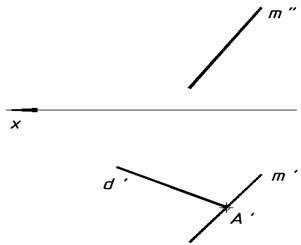 38*. Отыскать расстояние между скрещивающимися прямыми s и m. 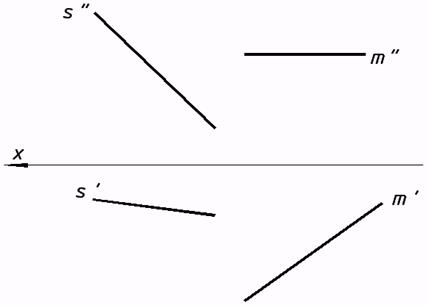 6. Методы преобразования ортогональных проекций |
||||||||||
39*. Выяснить длину отрезка прямой неспециализированного положения методом вращения около оси i ^p2. 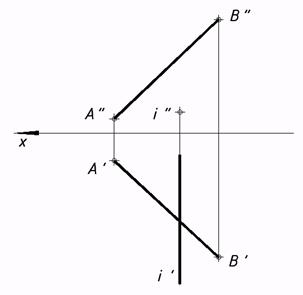
|
40. Перевести отрезок AB в положение, перпендикулярное p1 методом плоско-параллельного перемещения. 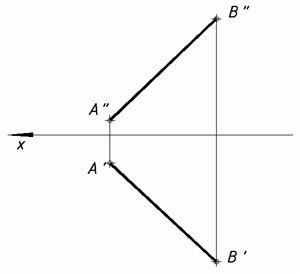
|
|||||||||
41*. Выяснить подлинную величину фигуры : a) методом замены плоскостей проекций; b) вращением около фронтали. 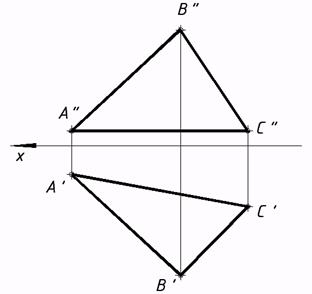 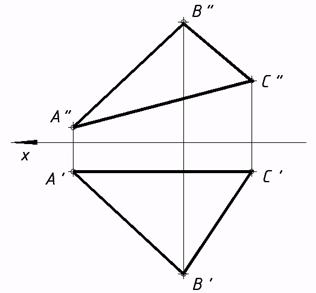
|
||||||||||
42*. Совместить плоскость ? с плоскостью ?2 вращением около фронтального следа плоскости. 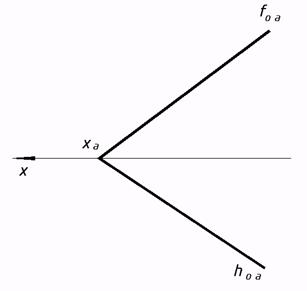
|
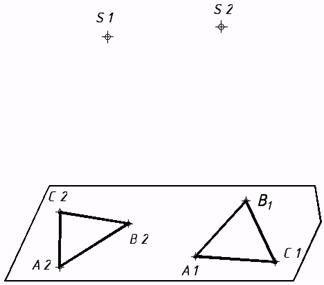
43*. Выстроить проекции равностороннего треугольника АВС, расположенного в плоскости ?, в случае, если известна горизонтальная проекция стороны АВ. Решить совмещением с плоскостью ?1. 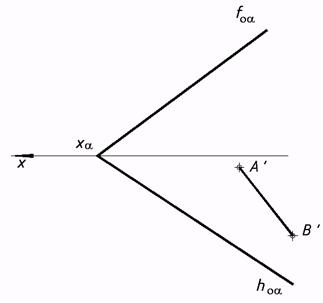
|
|||||||||
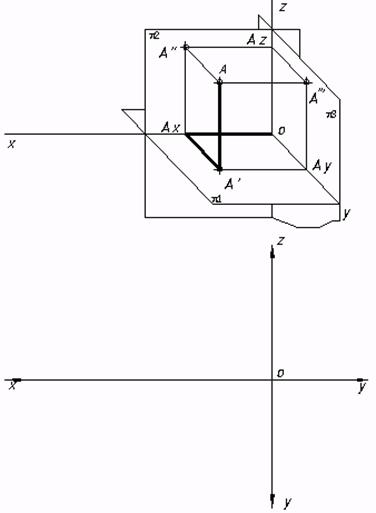
44. Выстроить проекции точки А в указанных совокупностях плоскостей проекций. 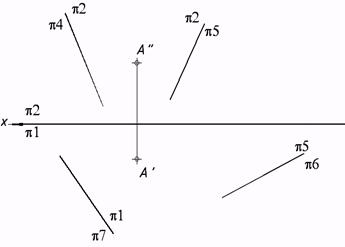
|
45*. Выяснить совокупности плоскостей проекций, в которых отрезок AB займет проецирующее положение, и выстроить его проекции. 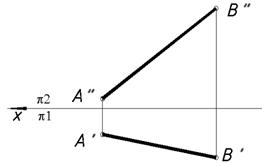
|
|||||||||
7. Метрические задачи. Определение 46. Выяснить расстояние от точки до прямой методом замены плоскостей проекций, начиная с замены плоскости ?2. 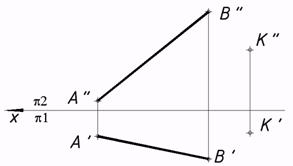 48*. Выяснить расстояние между заданными параллельными плоскостями методом замены плоскостей проекций. 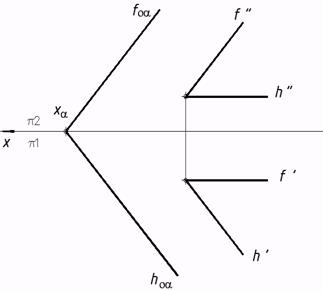
|
величин и расстояний углов. 47*. Выяснить расстояние между параллельными прямыми методом замены плоскости проекций, начиная с замены плоскости ?1. 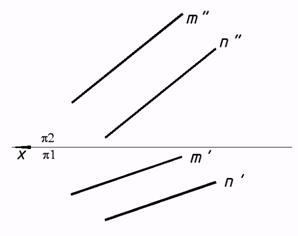 49*. Выяснить расстояние между плоскостью b и параллельной ей прямой m методом замены плоскостей проекций. 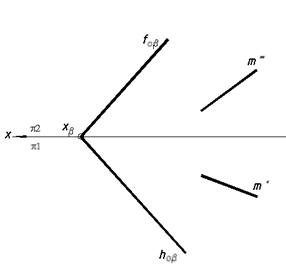
|
|||||||||
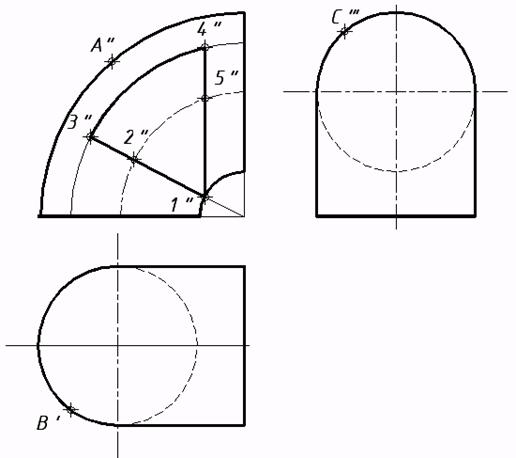
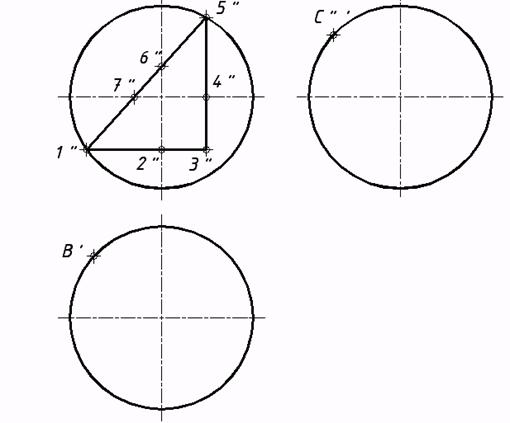
50*. Выяснить расстояние между скрещивающимися прямыми методом замены плоскостей проекций. 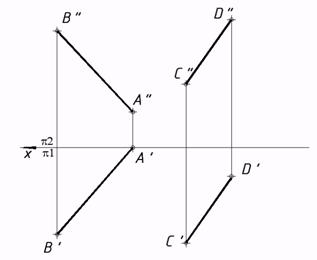 51*. Выстроить проекции окружности, рас- 52*. Выяснить углы наклона плоскости положенной в плоскости a, в случае, если даны ее центр C треугольника к плоскостям проекций. и радиус R=15мм. Решить заменой плоскостей проекций. Решить заменой плоскостей проекций. 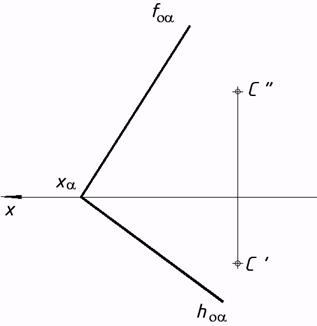 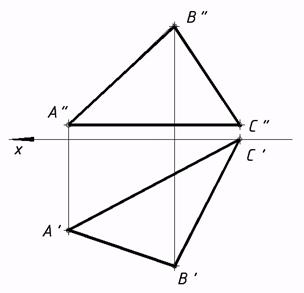 53*. Выяснить угол между плоскостями методом замены плоскостей проекций. 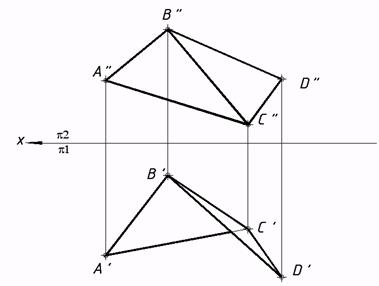
|
||||||||||
54. Выяснить расстояние от точки до прямой методом вращения около горизонтали. 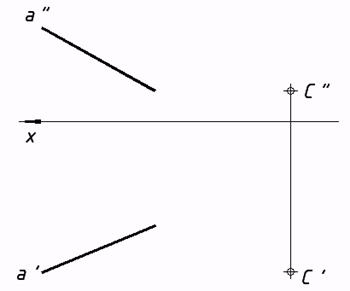 55*. Выяснить угол между плоскостью способом и прямой вращения около горизонтали. 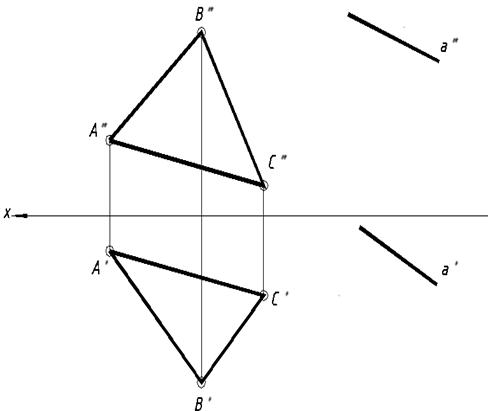 56*. Выяснить угол между плоскостями методом вращения около фронтали. 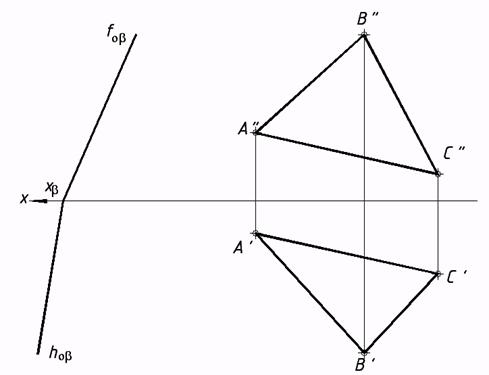 8. Поверхности. линия и Точка на поверхности. |
||||||||||
57*. Выяснить недостающие проекции точек a)конической; 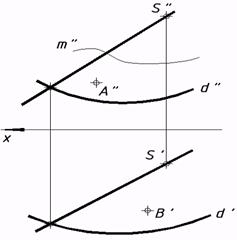 c) прямого цилиндроида; 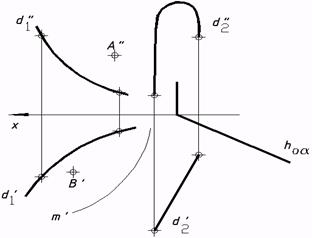 e) косой плоскости; выстроить фронтальный очерк поверхности; 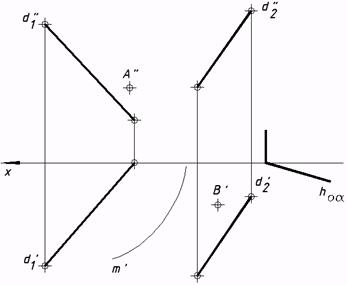
|
и линий, которыми владел заданным поверхностям: b)цилиндрической, 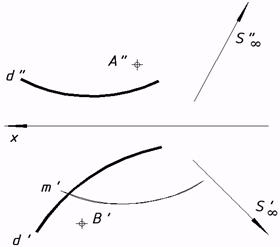 d) прямого коноида; 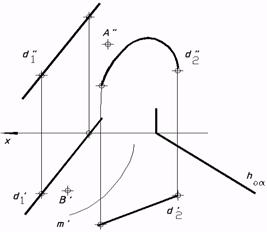 f) поверхности вращения 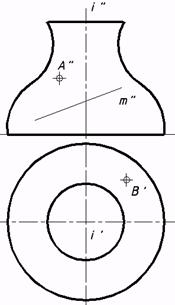
|
|||||||||
58*. Выяснить недостающие проекции линий и точек, которыми владел поверхностям: a) прямого геликоида; b) косого геликоида. Выстроить очерк геликоида 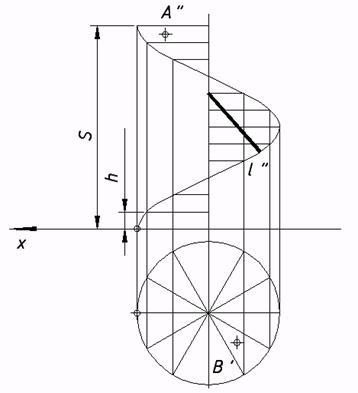 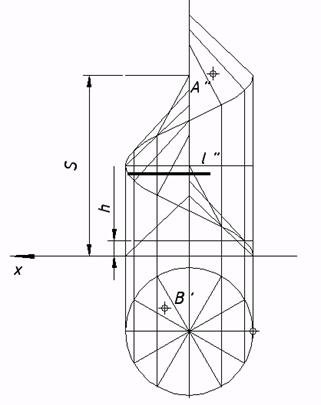 59*. Выяснить недостающие проекции точек, которыми владел поверхностям вращения. Выстроить очерки поверхностей: a) конической, b) однополостного гиперболоида. 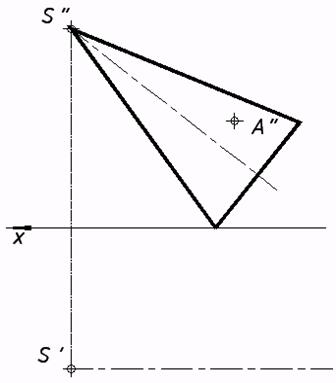 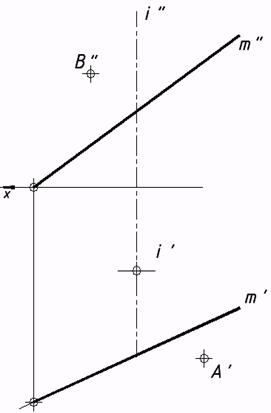 . |
||||||||||
| 9. Пересечение поверхностей с прямой и плоскостью. Касательные плоскости. 60*. Выстроить линии пересечения заданных плоскостей со следующими поверхностями: | ||||||||||
a) цилиндрической; 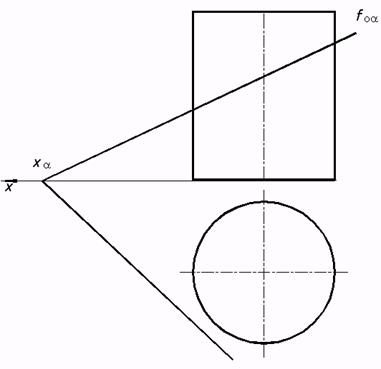
|
||||||||||
с) сферической; d) торовой. 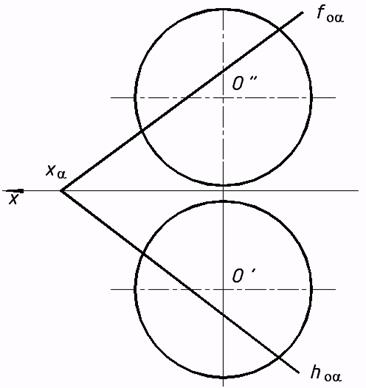 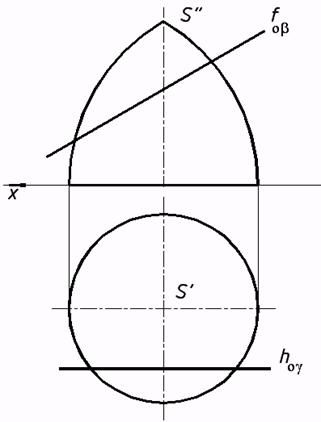
|
||||||||||
61*. Через точку совершить плоскость и нормаль, а) цилиндрической; 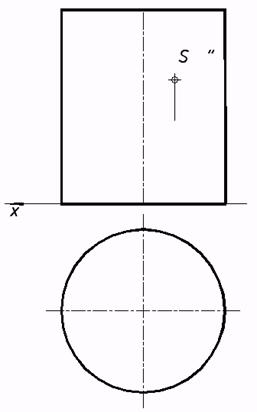
|
касательную к следующим поверхностям: b) конической; 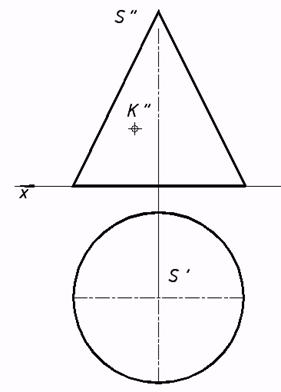
|
|||||||||
с) сферической; 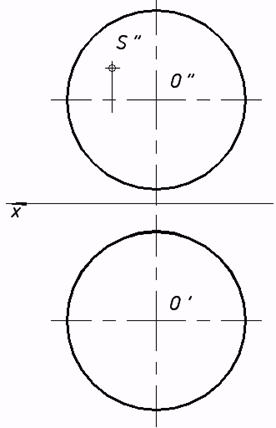
|
d) косой плоскости. 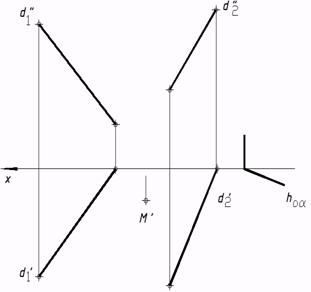
|
|||||||||
e) торовой. 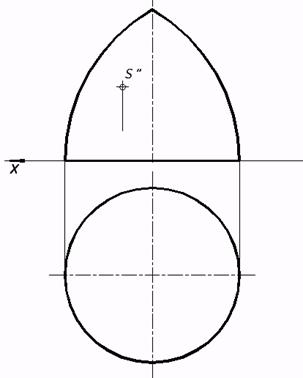
|
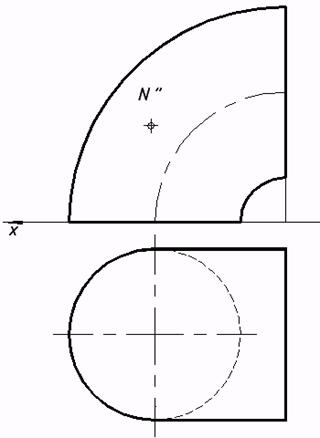
|
|||||||||
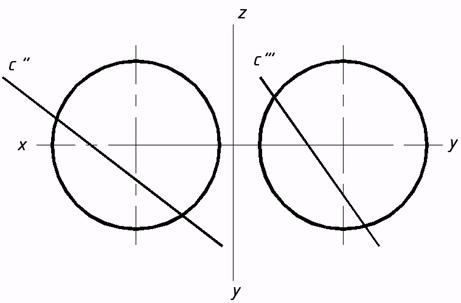
62*. Выстроить точки пересечения прямых с видимости): a)цилиндрической, 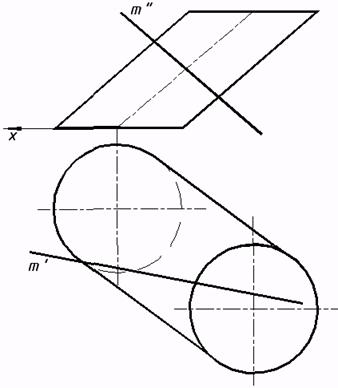 с) сферической (заменой плоскостей проекций), |
с заданными поверхностями, (выполняя условия b) конической; 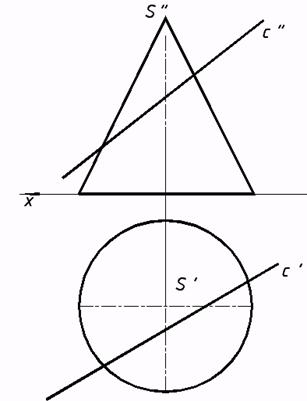
|
|||||||||
|
||||||||||
d) торовой; 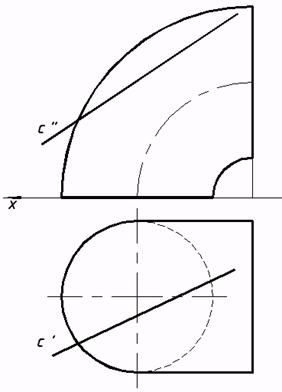
|
e) косой плоскости; 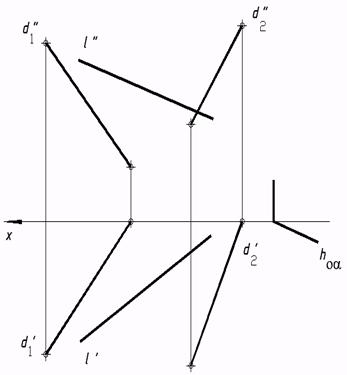
|
|||||||||
| 10. Обоюдное пересечение поверхностей | ||||||||||
63*. Выстроить проекции линий пересечения заданных поверхностей посредством метода запасных проецирующих плоскостей (рис. a, b, c, d, e, f): a) двух цилиндров; 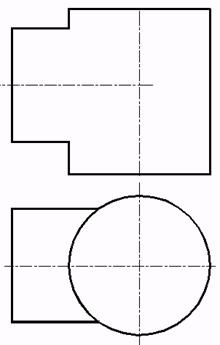
|
||||||||||
b) конуса и цилиндра; 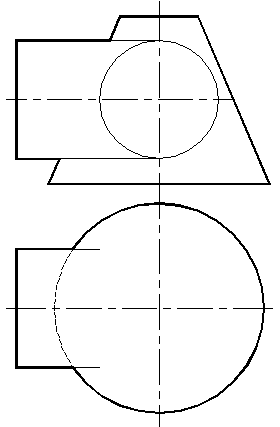
|
||||||||||
с) 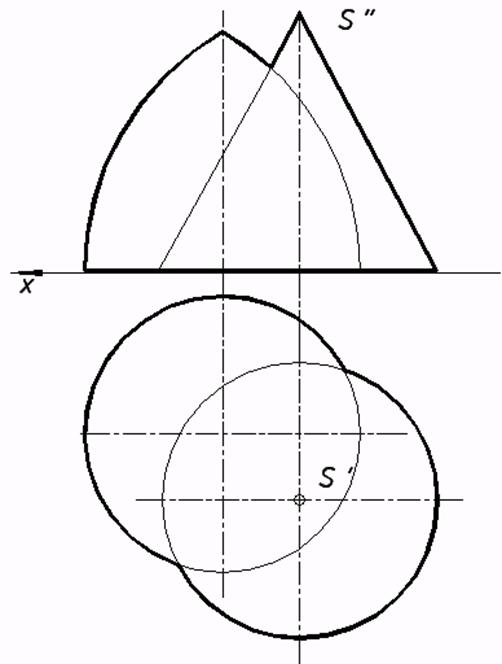 с) цилиндра и усечённого конуса; 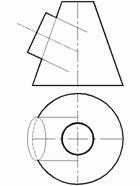
|
||||||||||
d) 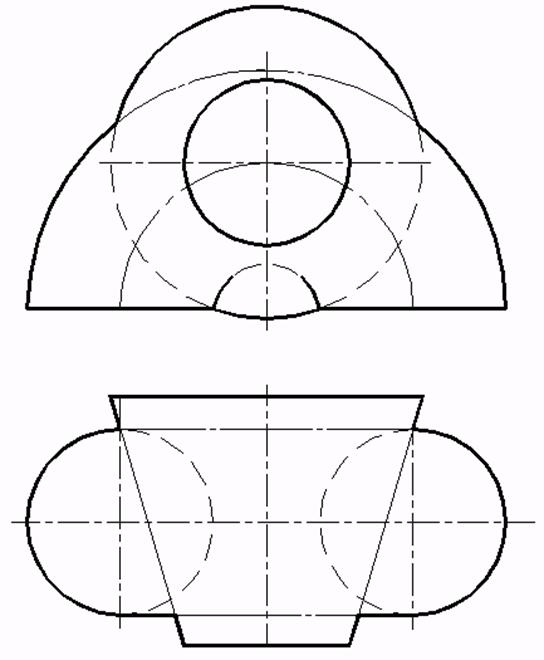
|
||||||||||
e) 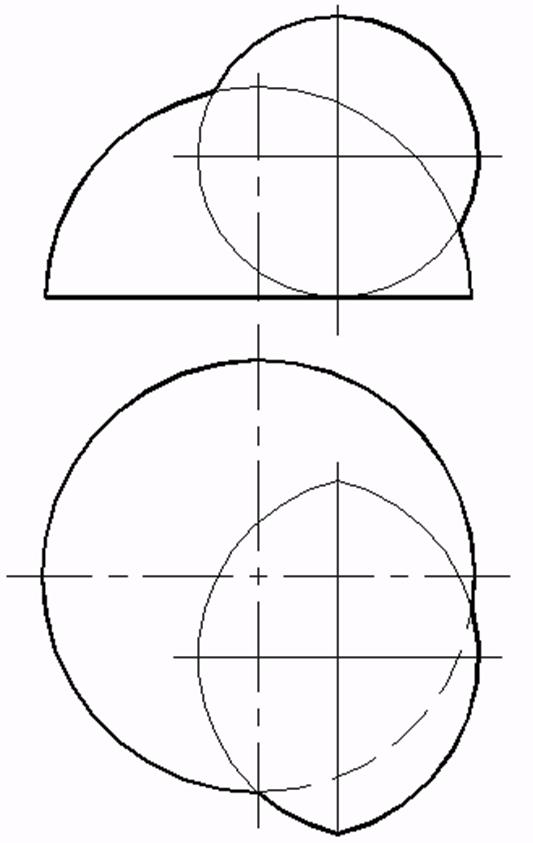
|
||||||||||
64*. Выстроить проекции линий пересечения заданных поверхностей посредством метода запасных концентрических сфер (рис. a, b, c, d, e, f): a) 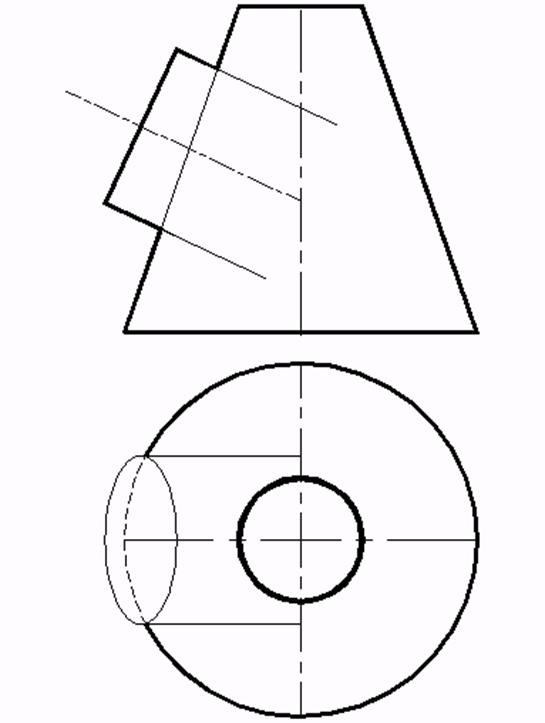
|
||||||||||
b) 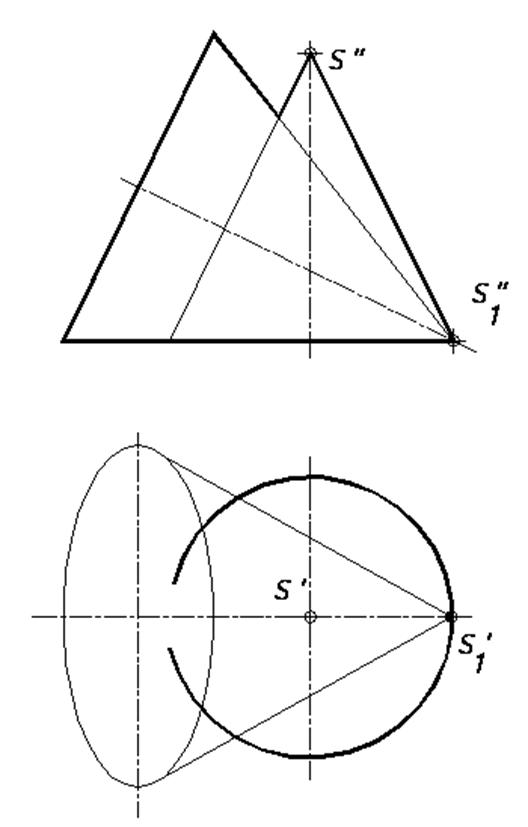 d) 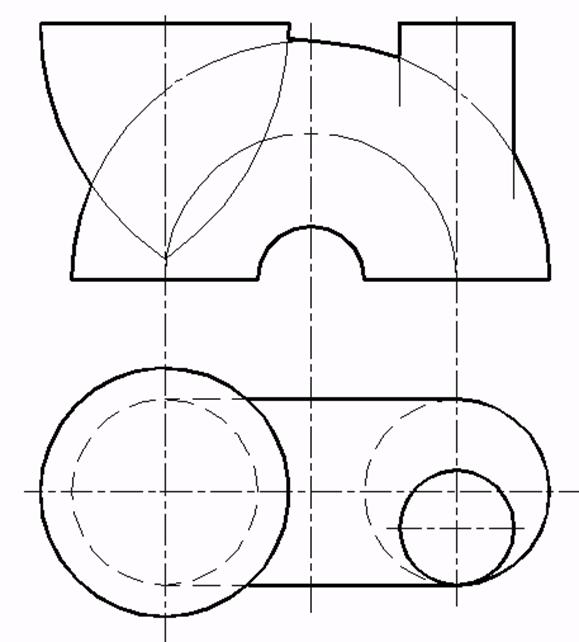
|
||||||||||
65*. Выстроить проекции линий пересечения заданных поверхностей посредством метода запасных эксцентрических сфер (рис. a, b, c):
a)
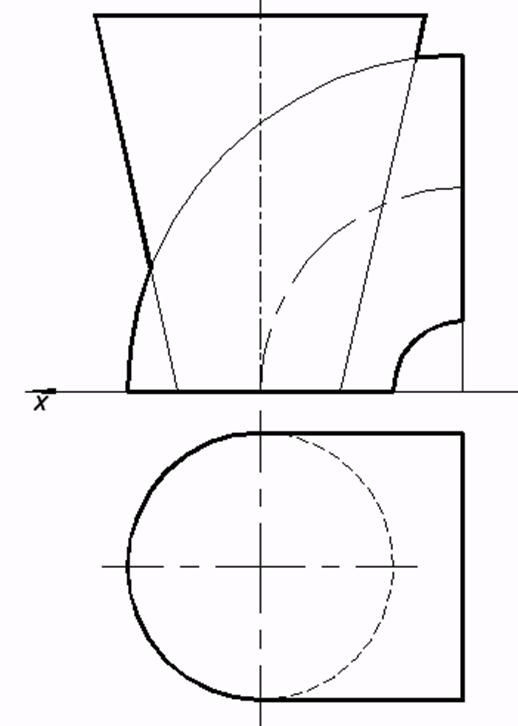
b) 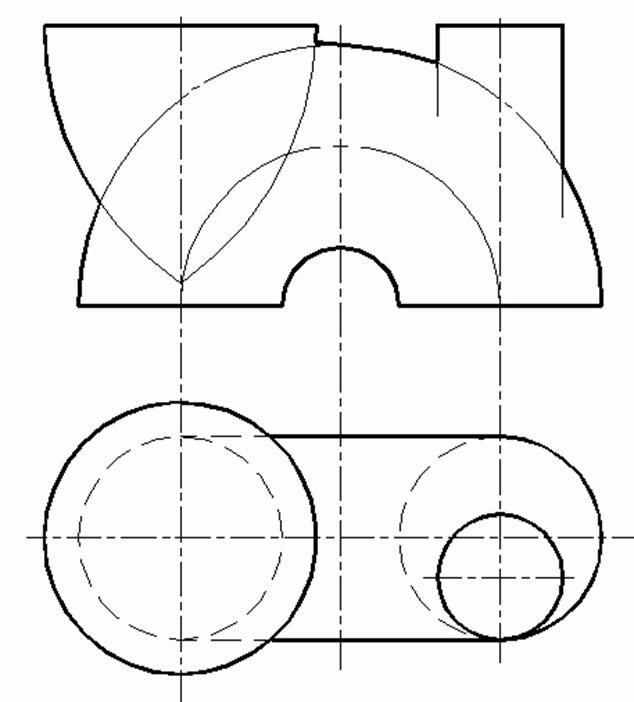
|
c)
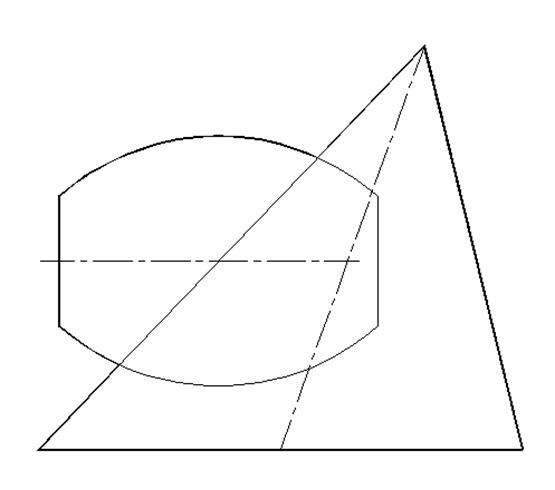
66. Выстроить линии пересечения заданных поверхностей, обрисованных около одной и той же сферы (рис. a, b):
a) двух цилиндров;
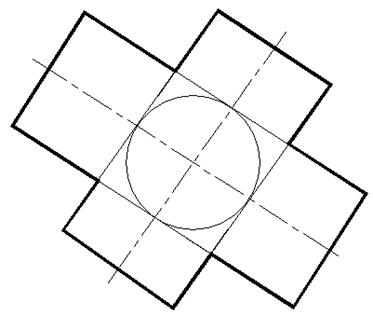
b) цилиндра и конуса;
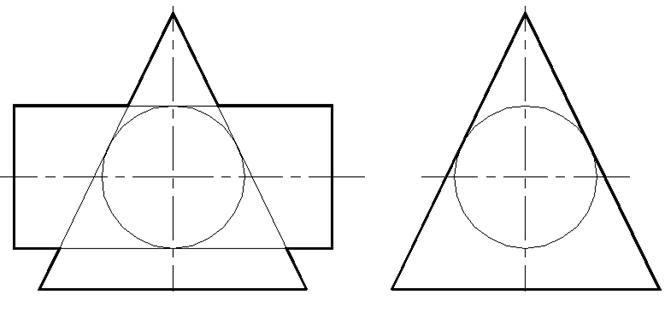
c) двух усечённых конусов
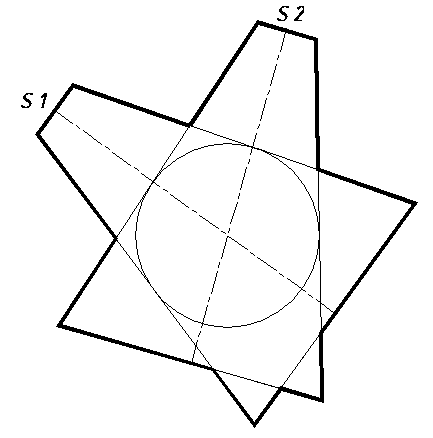
11. Проецирование геометрических моделей и тел 67*. Выстроить недостающие проекции линий и точек, расположенных на поверхностях заданных фигур: а) призмы; 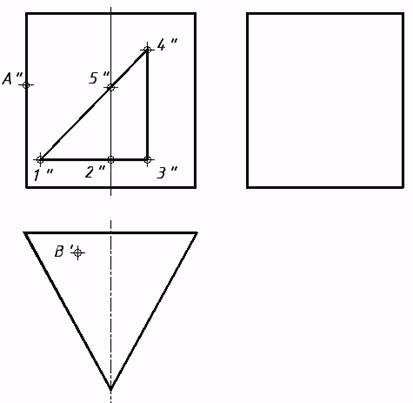 b) пирамиды; 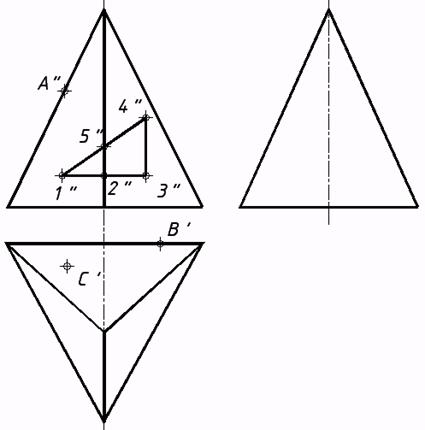
|
c) цилиндра;
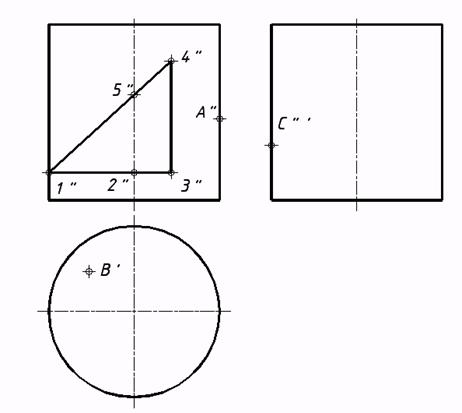
d) конуса;
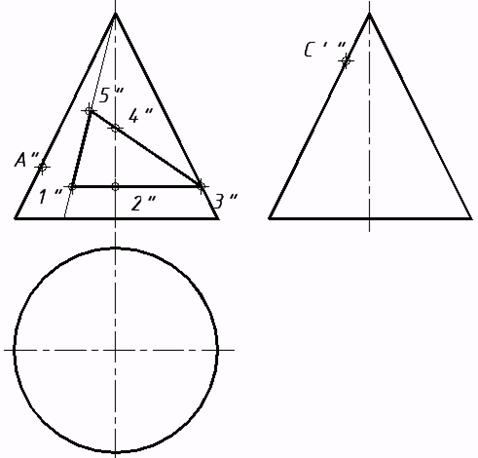
e) сферы;.
f) тора.