размерности и Обозначения
— пористость — m — доли единиц либо проценты;
— просветность — n — доли единиц либо проценты;
— гранулометрический состав — проценты от массового либо счетного содержания;
— действенный диаметр — d — м (СИ), см (СГС, техническая);
— радиус пор — R — м (СИ), см (СГС, техническая);
— проницаемость –k – м2, мкм2 (СИ), д (дарси) (СГС, техническая)
— скорость фильтрации – u – м/с (СИ), см/с (техническая);
— динамическая вязкость — m — Па.с(кг/м.с) (СИ), спз (10-2пз=10-2г/см.с) (техническая);
— кинематическая вязкость — n=m/r — м2/с (СИ), сст (10-2ст=10-2см2/с) (техническая);
— давление – р – Па (СИ), ат (техническая);
— плотность — r — кг/м3 (СИ), кГ.с2/м4 (техническая);
— удельный вес — g — кг/м2.с2 (СИ), кГ/м3 (техническая).
— пористость — m — доли единиц либо проценты;
— объемный дебит – Q=uF -м3/с (СИ), см3/с (техн.);
— массовый дебит –G=rQ – кг/с (СИ), кГ/с (техн);
— площадь фильтрации F – м2
1д » 1мкм2=10-12м2;
1 Па » 10-5ат;
1 Па.с » 103спз;
1 м2/с = 106сст.
ОПРЕДЕЛЕНИЕ ФИЛЬТРАЦИОННО-ЁМКОСТНЫХ ПАРАМЕТРОВ КОЛЛЕКТОРОВ.
ТЕОРИЯ
Настоящие пористые среды в подземной гидромеханике представляются идеализированными моделями — фиктивным и совершенным грунтами. Фиктивный — среда, складывающаяся из шариков, например, одного размера, совершенный — параллельные трубочки одного либо различного диаметра.
Главные характеристики пористых сред: пористость, просветность, гранулометрический состав, действенный диаметр либо гидравлический диаметр пор, удельная поверхность, механические особенности (упругость, пластичность, сопротивление сжатию и разрыву). Помимо этого, введены параметры, которые связаны с жидкостью: проницаемость и насыщенность.
Определения и расчетные зависимости
Пористость — это отношение количества пор Vп к количеству пористой среды V
m=Vп /V1.1
Пористость не редкость полная, открытая, действенная. В последнем случае под количеством пор понимается количество открытых пор занятых подвижной жидкостью, т.е. того количества через что может протекать жидкость.
Просветность — это отношение площади просветов fп ко всей площади сечения f
n=fп /f1.2
Удельная поверхность — это суммарная площадь поверхности частиц, содержащихся в единице количества пористой среды.
Насыщенность — это отношение количества жидкости Vf, содержащейся в порах, к количеству пор Vп
ef= Vf /Vп1.3
Проницаемость — это параметр породы, характеризующий ее свойство пропускать жидкие и газообразные среды. Физический суть проницаемости k содержится в том, что она характеризует площадь сечения каналов пористой среды, по которым происходит фильтрация.
Проницаемость разделяют на полную, фазовую и относительную. Безотносительная — характеризует физические особенности породы и определяется при наличии только какой-либо одной фазы, химически инертной по отношению к породе. Фазовая — проницаемость пород для данного газа либо жидкости при наличии в порах многофазных совокупностей. Относительная — отношение фазовой к безотносительной.
Пористая среда.
Для фиктивного грунта, исходя из геометрических построений, Слихтер вывел зависимость для полной пористости
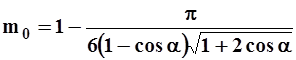 . 1.4
. 1.4
Из формулы (1.4) имеем mo=0,259 приa=60о и mo=0,476 при a=90о.
Просветность n фиктивного грунта вычисляется по формуле
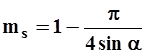 , 1.5
, 1.5
что даёт ms=0,0931 при a=60о и ms=0,476 при a=90о.
. Действенный диаметр определяют по гранулометрическому составу , н.п. по формуле веса средней частицы
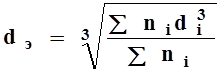 , 1.6
, 1.6
где di — средний диаметр i -ой фракции; ni — массовая либо счетная часть i — ой фракции.
Для совершенного грунта имеется сообщение радиуса пор с диаметром частиц фиктивного грунта
R=md / [12 (1-m)].1.7
.
Для фиктивного грунта
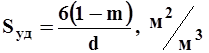 1.8
1.8
Удельная поверхность нефтесодержащих пород с достаточной точностью определяется формулой
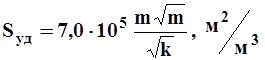 1.9
1.9
где k — проницаемость в дарси [мкм2].
Среднее значение Sуд для нефтесодержащих пород изменяется в пределах 40тыс. — 230тыс.м2/м3. Породы с удельной поверхностью большей 230тыс. м2/м3 непроницаемы либо слабопроницаемы (глины, глинистые пески и т.д.).
Величина проницаемости зависит от размера пор для модели совершенного грунта с трубками радиуса R
k=mR2/8,1.10
где R — мкм; k — д.
Для настоящих сред радиус пор связан с проницаемостью формулой Котяхова
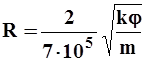 , 1.11
, 1.11
где k -д; R — м; j — структурный коэффициент (j=0.5035/m1,1 — для зернистых сред).
Т.к. радиус пор связан с удельной поверхностью, то с ней связана и проницаемость
Sуд=2m/k, 1.12
Проницаемость горных пород изменяется в широких пределах: крупнозернистый песчаник — 1-0.1д; плотные песчаники — 0.01-0.001д.
Параметры трещинной среды.
Трещиноватость — отношение количества трещин Vт ко всему количеству Vтрещинной среды.
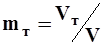 . 1.13
. 1.13
Для трещинно-пористой среды вводят суммарную (неспециализированную) пористость, прибавляя к трещиноватости пористость блоков.
Густота трещин Гт- это отношение полной длиныa li всех трещин, находящихся в данном сечении трещинной породы к удвоенной площади сечения f
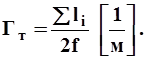 1.14
1.14
Из (1.16) направляться, что для идеализированной трещинной среды
mт=aтГdт, 1.15
где dт — раскрытость; aт — безразмерный коэффициент, равный 1,2, 3 для одномерного, плоского и пространственного случаев, соответственно.
Для настоящих пород значение коэффициента a зависит от геометрии совокупностей трещин в породе.
Для квадратной сетки трещин (плоский случай) Гт=1 / lт, гдеlт -размер блока породы. Средняя протяженность трещин l* равняется среднему размеру блока породы и равна
l*=1 / Гт .1.16
Трещинный пласт — деформируемая среда. В первом приближении можно считать
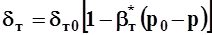 , 1.17
, 1.17
где dт0 — ширина трещины при начальном давлении р0 ; b*т=bп l/dт0 — сжимаемость трещины; bп — сжимаемость материалов блоков;l- среднее расстояние между трещинами.
Для трещинных сред l/dт100 .
Проницаемость трещиноватых сред равна
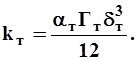 1.18
1.18
Для трещиновато-пористой среды неспециализированная проницаемость определяется как сумма межзерновой и трещинной проницаемостей.
ЗАДАЧИ
Задача 1
Выяснить пористость m, просветность n фиктивного грунта, в случае, если угол укладки частиц a равен 60о, 70о, 80о, 90о. Выстроить график зависимости данных размеров от угла укладки.
Задача 2.
Для величины пористости при a=75о (забрать из графика задачи 1) и диаметру частиц d=0,11 мм выяснить удельную поверхность Sуд фиктивного грунта, радиус пор совершенного грунта R , проницаемость k совершенного грунта, проницаемость и удельную поверхность настоящего грунта.
Задача 3.
Выяснить густоту трещин Г, среднюю длину l* одномерой. двухмерной и трехмерной моделей трещинной среды, в случае, если трещинная проницаемость kт=0,1д и ширина трещины dт=0,2 мм.
ЗАКОН ДАРСИ.
ТЕОРИЯ
Закон Дарси либо линейный закон фильтрации, устанавливает линейную связь между утратой напора Н1-Н2 и объёмным расходом жидкости Q= u.F, текущей в трубке с площадью поперечного сечения F ,заполненной пористой средой. Напор для несжимаемой жидкости имеет форму 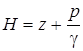 , где z- высота положения;р/g — пьезометрическая высота; g — объёмный вес.
, где z- высота положения;р/g — пьезометрическая высота; g — объёмный вес.
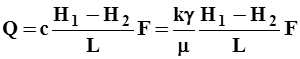 , 2.1
, 2.1
где с — коэффициент пропорциональности, именуемый коэффициентом фильтрации и имеющий размерность скорости.
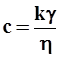 . 2.2
. 2.2
2.2. ЗАДАЧИ
Адача 1
Выяснить коэффициент фильтрации проницаемость, в случае, если как мы знаем, что площадь поперечного сечения горизонтально расположенного примера песчаника F=30см2, протяженность примера L=15 см, разность давлений на входе жидкости в пример и на выходе Dp=0,2aт, удельный вес жидкости g = 1000 кГ/м3, динамический коэффициент вязкости m=4 спз и расход Q равен 5 л/час.
Ответ: с=3,47 . 10-3 см/сек.
Задача 2
Выяснить скорость фильтрации u и среднюю скорость перемещения нефти w у стены гидродинамически идеальной скважины и на расстоянии r=75 м от скважины, в случае, если как мы знаем, что мощность идаста h = 10 м, пористость его т=12%, радиус скважины rc= 0,1 м, весовои дебит скважины G= 50 т/сут, и плотность нефти r= 850 кг/м3.
Ответ: wc = 1,087 ,10-4 м/сек; uc= 0,91 ,10-4 м/сек;
w = 1,45 ,10-7 м/сек; u= 1,206 ,10-6 м/сек.
Задача3
Выяснить скорость фильтрации газа у стены гидродинамически идеальной скважины, в случае, если как мы знаем, что приведенный к атмосферному давлению объемный расход газа Qат=1 млрд м3/сут, радиус скважины rc= 0,1 м, мощность пласта h=20 м, полное давление газа на забое pc= 50 am.
Ответ:
Из уравнения неразрывности для установившегося потока
G= Qr=Qатrат=сonst, 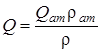
Из уравнения состояния совершенного газа при изотермическом ходе направляться, что
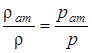 ,
,
исходя из этого объемный дебит на забое
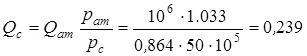 м3/с
м3/с
Скорость фильтрации
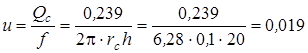 м/с.
м/с.
Задача4
Через два однородных примера пористой среды, содержащих глинистые частицы, с целью коэффициента коэффициента фильтрации и определения проницаемости пропускали:
а) питьевую воду при t=20°C при перепаде давления Dр= 500 мм рт. ст. с расходом Q=2 см3/мин,
в) соленую воду с удельным весом g=1103 кГ/м3 и вязкостью m=1,1 спз при той же разности давления, что и при а) и с расходом Q=0,12 см3/с Размеры образцов: протяженность L=5 см, площадь поперечного сечения f=5 см2. Отыскать отношение проницаемостей для случаев аи в.
Ответ:
При одномерной, прямолинейно-параллельной установившейся фильтрации несжимаемой жидкости по закону Дарси определим k из формулы:
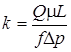 .
.
Определим значение
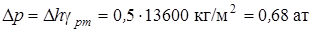
Учитывая, что при t=20°C для пресной воды g= 1000 кГ/м3, а m= 1 спз, возьмём
а) 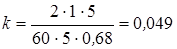 д
д
ТЕОРИЯ
Верхняя граница. Критерием верхней границы справедливости закона Дарси в большинстве случаев помогает сопоставление числа Рейнольдса Re=war/h с его критическим значением Reкр, по окончании которого линейная связь между расходом и потерей напора нарушается. В выражении для числа Re:w -характерная скорость течения: а — характерный геометрический размер пористой среды; r — плотность жидкости. Имеется последовательность представлений чисел Рейнольдса, взятых разными авторами при том либо другом обосновании характерных параметров. Приведём кое-какие из данных зависимостей самый употребляемые в подземной гидромеханике:
а) Павловского
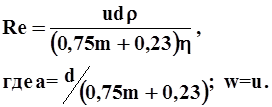 3.1
3.1
Критическое число Рейнольдса Reкр=7,5-9.
б) Щелкачёва
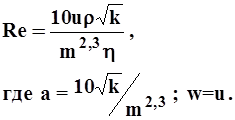 3.2
3.2
Критическое число Рейнольдса Reкр=1-12.
в) Миллионщикова
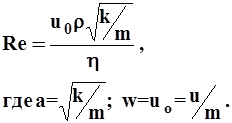 3.3
3.3
Критическое число Рейнольдса Reкр=0,022-0,29.
В случае, если вычисленное по одной из формул (3.1-3.3) значение числа Re оказывается меньше нижнего критического значения Reкр, то закон Дарси честен, в случае, если Re больше верхнего значения Reкр, то закон Дарси заведомо нарушен.
Скорость фильтрации uкр, при которой нарушается закон Дарси, именуется критической скоростью фильтрации.
Нижняя граница
Модель с предельным градиентом
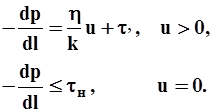 3.4
3.4
Нелинейный закон
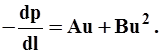 3.5
3.5
Коэффициенты А и В определяются или экспериментально, или теоретически. В последнем случае
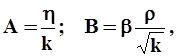 3.6
3.6
где b- структурный коэффициент и по Минскому определяется выражением
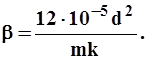 3.7
3.7
ЗАДАЧИ
Задача 1
Найти значение числа Рейнольдса у стены гидродинамическп несовершенной по характеру вскрытия нефтяной скважины, в случае, если как мы знаем, что аксплуатационная колонна перфорирована, на каждом погонном метре колонны прострелено 10 отверстий диаметром d0 = 10 мм, мощность пласта h=15м,, проницаемость пласта k=l д, пористость т = 18%, коэффициент вязкости нефти m = 4 спз, плотность нефти ? = 870 кг/м3 и дебит скважины образовывает 140м3/сут.
Ответ: Re = 15,6 (по формуле Щелкачева),
Re = 0,396 (по формуле Миллионщикова).
Задача 2
Выяснить радиус призабойной территории rкр, в которой совершить правонарушение Дарси, при установившейся плоско-радиальной фильтрации совершенного газа, в случае, если как мы знаем, что приведенный к атмосферному давлению дебит скиажины Qат =2.106 м3/сут, мощность пласта h = 10 м, проницаемость k = 0,6д,пористость пласта m =19%, динамический коэффициент вязкости газа в пластовых условиях m =1,4.10-5 Па. с, плотность газа при пластовой температуре и атмосферном давлении ?ат = 0,7 кг/м3
Указание. В ответе применять число Рейнольдса по формуле М. Д. Миллионщикова и за Reкр забрать нижнее значение Reкр = 0,022.
Ответ:
По М. Д. Миллионщикову 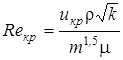 ,
,
откуда
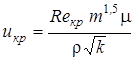 , 1
, 1
где
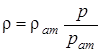 . 2
. 2
Иначе
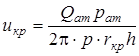 . 3
. 3
Подставляя (2) в (1) и приравнивая выражения (1) и (3), возьмём
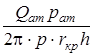 =
= 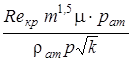 ,
,
откуда
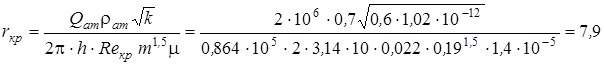 м.
м.
Задача 3
Выяснить, происходит ли фильтрация н пласте по закону Дарен, в случае, если как мы знаем, что дебит нефтянои скважины Q = 200 m3/cуt, мощность пласта h=5м, коэффициент пористости т = 16%, коэффициент проницаемости k=0,2 д, плотность нефти ?=0,8 г/см3, вязкость ее m=5спз. Скважина гидродинамически идеальна, радиус ее rc=0,1 м.
Ответ: Отыщем скорость фильтрации на забое скважины
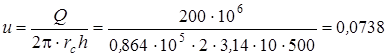 cм/c
cм/c
Определим число Рейнольдса по Щелкачеву и сопоставим его с критическим значением.
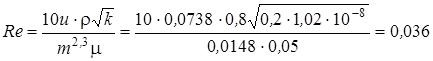 ,
,
.
Задача 4
Дебит газовой скважины, приведенный к атмосферному давлению при пластовой температуре Qат=2•106 м3/сут, безотносительное давление на забое рс=80ат, мощность пласта h= 10 м, коэффициент пористости пласта т= 18%, коэффициент проницаемости k=1,2д , средний молекулярный вес газа М=18, динамический коэффициент вязкости в пластовых условиях m = 0,015 спз, температура пласта 45°С.
Выяснить, имеет ли место фильтрация по закону Дарен в призабойной территории идеальной скважины радиусом rc= 10 см.
Ответ:
Определим плотность газа у забоя скважины. Для этого отыщем плотность газа при 0°С и при давлении в 1,033ат
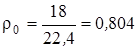 кг/м3,
кг/м3,
и при условиях на забое
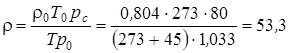 кг/м3.
кг/м3.
Скорость фильтрации на забое равна
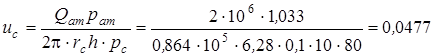 м/с
м/с
Число Рейнольдса
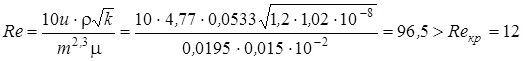 ,
,
т. е. в призабойной территории нарушается закон Дарси.
ТЕОРИЯ
Одномерным именуется поток, в котором параметры являются функцией лишь одной пространственной координаты, направленной по линии тока. К одномерным потокам относятся:
1) прямолинейно-параллельный:
2) плоскорадиальный;
3) радиально-сферический.
При условии вытеснения флюида из пласта либо его нагнетания в пласт через галерею либо скважину условимся принимать за координату произвольной точки пласта расстояние r до данной точки от:
1) галереи ( для прямолинейно- параллельного потока);
2) центра контура скважины в главной плоскости (плоскости подошвы пласта) фильтрации (для плоско-радиального потока);
3) центра полусферического забоя скважины (для сферически-радиального потока).
Течение в пласте считается потенциальным, т.е. существует некая функция j, именуемая потенциалом, градиент которой равен соответствующим проекциям вектора количества перемещения (массового расхода)
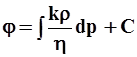 . 4.1.
. 4.1.
, где F – площадь притока
Плоско-радиальный поток
* изменение потенциальной функции
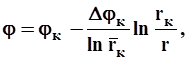 4.1
4.1
где 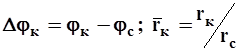 ;
;
* индикаторная зависимость (уравнение притока)
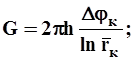 4.2
4.2
Для несжимаемой жидкости уравнение носит название – уравнение Дюпюи
* изменение градиента потенциала
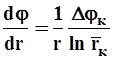 . 4.3
. 4.3
Потенциальные функции
ЗАДАЧИ
Задача 1
Вычислить индикаторные кривые, нанести на график и проанализировать при плоско-радиальном притоке для: несжимаемой жидкости в пористом и трещиноватом пластах, газа в пористом пласте.
Данные: рст=1ата; rст=0,91кг/м3; b* = 0,008.10-5 м2/н.
hг=0,2сПз; hж=2сПз; k=k0=0,1д; h=6м; rк=200м; rс=5,1 см
Задача 2
2. Выяснить скорости и изменение давления по радиусу r (3-4 значения), нанести на график и проанализировать при плоско-радиальном притоке для: несжимаемой жидкости в пористом и трещиноватом пластах, газа в пористом пласте.
Данные: рст=1ата; rст=0,91кг/м3; b* = 0,008.10-5 м2/н.
hг=0,2сПз; hж=2сПз; k=k0=0,1д; h=6м; rк=200м; rс=5,1 см
размерности и Обозначения
— пористость — m — доли единиц либо проценты;
— просветность — n — доли единиц либо проценты;
— гранулометрический состав — проценты от массового либо счетного содержания;
— действенный диаметр — d — м (СИ), см (СГС, техническая);
— радиус пор — R — м (СИ), см (СГС, техническая);
— проницаемость –k – м2, мкм2 (СИ), д (дарси) (СГС, техническая)
— скорость фильтрации – u – м/с (СИ), см/с (техническая);
— динамическая вязкость — m — Па.с(кг/м.с) (СИ), спз (10-2пз=10-2г/см.с) (техническая);
— кинематическая вязкость — n=m/r — м2/с (СИ), сст (10-2ст=10-2см2/с) (техническая);
— давление – р – Па (СИ), ат (техническая);
— плотность — r — кг/м3 (СИ), кГ.с2/м4 (техническая);
— удельный вес — g — кг/м2.с2 (СИ), кГ/м3 (техническая).
— пористость — m — доли единиц либо проценты;
— объемный дебит – Q=uF -м3/с (СИ), см3/с (техн.);
— массовый дебит –G=rQ – кг/с (СИ), кГ/с (техн);
— площадь фильтрации F – м2
1д » 1мкм2=10-12м2;
1 Па » 10-5ат;
1 Па.с » 103спз;
1 м2/с = 106сст.
ОПРЕДЕЛЕНИЕ ФИЛЬТРАЦИОННО-ЁМКОСТНЫХ ПАРАМЕТРОВ КОЛЛЕКТОРОВ.
ТЕОРИЯ
Настоящие пористые среды в подземной гидромеханике представляются идеализированными моделями — фиктивным и совершенным грунтами. Фиктивный — среда, складывающаяся из шариков, например, одного размера, совершенный — параллельные трубочки одного либо различного диаметра.
Главные характеристики пористых сред: пористость, просветность, гранулометрический состав, действенный диаметр либо гидравлический диаметр пор, удельная поверхность, механические особенности (упругость, пластичность, сопротивление сжатию и разрыву). Помимо этого, введены параметры, которые связаны с жидкостью: проницаемость и насыщенность.
Определения и расчетные зависимости
Пористость — это отношение количества пор Vп к количеству пористой среды V
m=Vп /V1.1
Пористость не редкость полная, открытая, действенная. В последнем случае под количеством пор понимается количество открытых пор занятых подвижной жидкостью, т.е. того количества через что может протекать жидкость.
Просветность — это отношение площади просветов fп ко всей площади сечения f
n=fп /f1.2
Удельная поверхность — это суммарная площадь поверхности частиц, содержащихся в единице количества пористой среды.
Насыщенность — это отношение количества жидкости Vf, содержащейся в порах, к количеству пор Vп
ef= Vf /Vп1.3
Проницаемость — это параметр породы, характеризующий ее свойство пропускать жидкие и газообразные среды. Физический суть проницаемости k содержится в том, что она характеризует площадь сечения каналов пористой среды, по которым происходит фильтрация.
Проницаемость разделяют на безотносительную, фазовую и относительную. Безотносительная — характеризует физические особенности породы и определяется при наличии только какой-либо одной фазы, химически инертной по отношению к породе. Фазовая — проницаемость пород для данного газа либо жидкости при наличии в порах многофазных совокупностей. Относительная — отношение фазовой к безотносительной.
Пористая среда.
Для фиктивного грунта, исходя из геометрических построений, Слихтер вывел зависимость для полной пористости
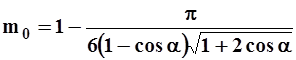 . 1.4
. 1.4
Из формулы (1.4) имеем mo=0,259 приa=60о и mo=0,476 при a=90о.
Просветность n фиктивного грунта вычисляется по формуле
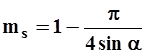 , 1.5
, 1.5
что даёт ms=0,0931 при a=60о и ms=0,476 при a=90о.
. Действенный диаметр определяют по гранулометрическому составу , н.п. по формуле веса средней частицы
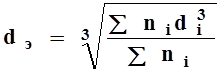 , 1.6
, 1.6
где di — средний диаметр i -ой фракции; ni — массовая либо счетная часть i — ой фракции.
Для совершенного грунта имеется сообщение радиуса пор с диаметром частиц фиктивного грунта
R=md / [12 (1-m)].1.7
.
Для фиктивного грунта
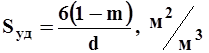 1.8
1.8
Удельная поверхность нефтесодержащих пород с достаточной точностью определяется формулой
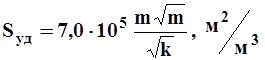 1.9
1.9
где k — проницаемость в дарси [мкм2].
Среднее значение Sуд для нефтесодержащих пород изменяется в пределах 40тыс. — 230тыс.м2/м3. Породы с удельной поверхностью большей 230тыс. м2/м3 непроницаемы либо слабопроницаемы (глины, глинистые пески и т.д.).
Величина проницаемости зависит от размера пор для модели совершенного грунта с трубками радиуса R
k=mR2/8,1.10
где R — мкм; k — д.
Для настоящих сред радиус пор связан с проницаемостью формулой Котяхова
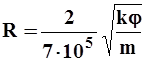 , 1.11
, 1.11
где k -д; R — м; j — структурный коэффициент (j=0.5035/m1,1 — для зернистых сред).
Т.к. радиус пор связан с удельной поверхностью, то с ней связана и проницаемость
Sуд=2m/k, 1.12
Проницаемость горных пород изменяется в широких пределах: крупнозернистый песчаник — 1-0.1д; плотные песчаники — 0.01-0.001д.
Параметры трещинной среды.
Трещиноватость — отношение количества трещин Vт ко всему количеству Vтрещинной среды.
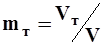 . 1.13
. 1.13
Для трещинно-пористой среды вводят суммарную (неспециализированную) пористость, прибавляя к трещиноватости пористость блоков.
Густота трещин Гт- это отношение полной длиныa li всех трещин, находящихся в данном сечении трещинной породы к удвоенной площади сечения f
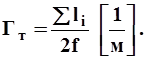 1.14
1.14
Из (1.16) направляться, что для идеализированной трещинной среды
mт=aтГdт, 1.15
где dт — раскрытость; aт — безразмерный коэффициент, равный 1,2, 3 для одномерного, плоского и пространственного случаев, соответственно.
Для настоящих пород значение коэффициента a зависит от геометрии совокупностей трещин в породе.
Для квадратной сетки трещин (плоский случай) Гт=1 / lт, гдеlт -размер блока породы. Средняя протяженность трещин l* равняется среднему размеру блока породы и равна
l*=1 / Гт .1.16
Трещинный пласт — деформируемая среда. В первом приближении можно считать
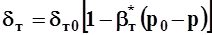 , 1.17
, 1.17
где dт0 — ширина трещины при начальном давлении р0 ; b*т=bп l/dт0 — сжимаемость трещины; bп — сжимаемость материалов блоков;l- среднее расстояние между трещинами.
Для трещинных сред l/dт100 .
Проницаемость трещиноватых сред равна
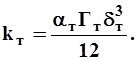 1.18
1.18
Для трещиновато-пористой среды неспециализированная проницаемость определяется как сумма межзерновой и трещинной проницаемостей.
ЗАДАЧИ
Задача 1
Выяснить пористость m, просветность n фиктивного грунта, в случае, если угол укладки частиц a равен 60о, 70о, 80о, 90о. Выстроить график зависимости данных размеров от угла укладки.
Задача 2.
Для величины пористости при a=75о (забрать из графика задачи 1) и диаметру частиц d=0,11 мм выяснить удельную поверхность Sуд фиктивного грунта, радиус пор совершенного грунта R , проницаемость k совершенного грунта, проницаемость и удельную поверхность настоящего грунта.
Задача 3.
Выяснить густоту трещин Г, среднюю длину l* одномерой. двухмерной и трехмерной моделей трещинной среды, в случае, если трещинная проницаемость kт=0,1д и ширина трещины dт=0,2 мм.
ЗАКОН ДАРСИ.
ТЕОРИЯ
Закон Дарси либо линейный закон фильтрации, устанавливает линейную связь между утратой напора Н1-Н2 и объёмным расходом жидкости Q= u.F, текущей в трубке с площадью поперечного сечения F ,заполненной пористой средой. Напор для несжимаемой жидкости имеет форму 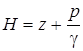 , где z- высота положения;р/g — пьезометрическая высота; g — объёмный вес.
, где z- высота положения;р/g — пьезометрическая высота; g — объёмный вес.
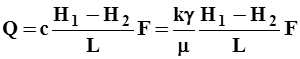 , 2.1
, 2.1
где с — коэффициент пропорциональности, именуемый коэффициентом фильтрации и имеющий размерность скорости.
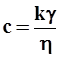 . 2.2
. 2.2
2.2. ЗАДАЧИ
Адача 1
Выяснить коэффициент фильтрации проницаемость, в случае, если как мы знаем, что площадь поперечного сечения горизонтально расположенного примера песчаника F=30см2, протяженность примера L=15 см, разность давлений на входе жидкости в пример и на выходе Dp=0,2aт, удельный вес жидкости g = 1000 кГ/м3, динамический коэффициент вязкости m=4 спз и расход Q равен 5 л/час.
Ответ: с=3,47 . 10-3 см/сек.
Задача 2
Выяснить скорость фильтрации u и среднюю скорость перемещения нефти w у стены гидродинамически идеальной скважины и на расстоянии r=75 м от скважины, в случае, если как мы знаем, что мощность идаста h = 10 м, пористость его т=12%, радиус скважины rc= 0,1 м, весовои дебит скважины G= 50 т/сут, и плотность нефти r= 850 кг/м3.
Ответ: wc = 1,087 ,10-4 м/сек; uc= 0,91 ,10-4 м/сек;
w = 1,45 ,10-7 м/сек; u= 1,206 ,10-6 м/сек.
Задача3
Выяснить скорость фильтрации газа у стены гидродинамически идеальной скважины, в случае, если как мы знаем, что приведенный к атмосферному давлению объемный расход газа Qат=1 млрд м3/сут, радиус скважины rc= 0,1 м, мощность пласта h=20 м, полное давление газа на забое pc= 50 am.
Ответ:
Из уравнения неразрывности для установившегося потока
G= Qr=Qатrат=сonst, 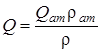
Из уравнения состояния совершенного газа при изотермическом ходе направляться, что
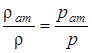 ,
,
исходя из этого объемный дебит на забое
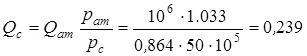 м3/с
м3/с
Скорость фильтрации
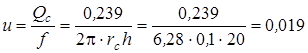 м/с.
м/с.
Задача4
Через два однородных примера пористой среды, содержащих глинистые частицы, с целью коэффициента коэффициента фильтрации и определения проницаемости пропускали:
а) питьевую воду при t=20°C при перепаде давления Dр= 500 мм рт. ст. с расходом Q=2 см3/мин,
в) соленую воду с удельным весом g=1103 кГ/м3 и вязкостью m=1,1 спз при той же разности давления, что и при а) и с расходом Q=0,12 см3/с Размеры образцов: протяженность L=5 см, площадь поперечного сечения f=5 см2. Отыскать отношение проницаемостей для случаев аи в.
Ответ:
При одномерной, прямолинейно-параллельной установившейся фильтрации несжимаемой жидкости по закону Дарси определим k из формулы:
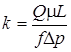 .
.
Определим значение
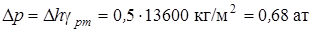
Учитывая, что при t=20°C для пресной воды g= 1000 кГ/м3, а m= 1 спз, возьмём
а) 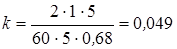 д
д