Кроме способа мельчайших квадратов, благодаря которому как правило определяются малоизвестные параметры модели регрессии, при линейной модели парной регрессии осуществим другой подход к ответу данной неприятности.
Линейная модель парной регрессии возможно записана в виде:
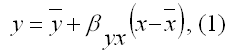
где у – значения зависимой переменной;
х – значения свободной переменной;
у – среднее значение зависимой переменной, которое определяется на основании выборочных данных вычисленное по формуле средней арифметической:
Коэффициенту В при растолковывающем факторе в парной линейной регрессии возможно дать естественную экономическую интерпретацию. Коэффициент показывает, на какую величину изменяется в среднем изучаемый эконометрический показатель при повышении растолковывающего фактора на одну единицу.
Итак. Параметр В x именуется выборочным коэффициентом регрессии переменной у по переменной х. Этот параметр показывает, на какое количество в среднем изменится зависимая переменная у при трансформации свободной переменной х на единицу собственного измерения.
Выборочный коэффициент регрессии переменной у по переменной х рассчитывается по формуле:
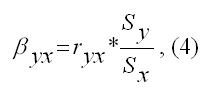
где ryx – это выборочный парный коэффициент корреляции между переменными у и х, что рассчитывается по формуле:
уx – среднее арифметическое значение произведения зависимой и свободной переменных:
Sy – показатель выборочного среднеквадратического отклонения зависимой переменной у. Данный показатель характеризует, на какое количество единиц в среднем отклоняются значения зависимой переменной у от её среднего значения. Он рассчитывается по формуле:
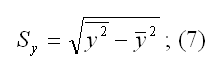
у2 — среднее значение из квадратов значений зависимой переменной у:
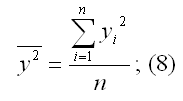
у2 — квадрат средних значений зависимой переменной у:
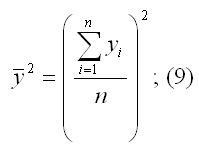
Sx – показатель выборочного среднеквадратического отклонения свободной переменной х. Данный показатель характеризует, на какое количество единиц в среднем отклоняются значения свободной переменной х от её среднего значения. Они рассчитывается по формуле:
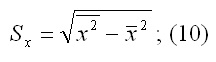
x2 — среднее значение из квадратов значений свободной переменной х:
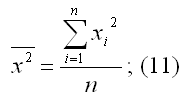
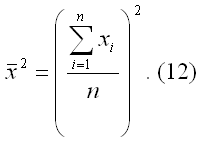
x2 — квадрат средних значений свободной переменной х:
При применении рассмотренного подхода оценивания малоизвестных параметров линейной модели парной регрессии, направляться учитывать что ryx=rxy, но ?yx??xy.
Оценка качества соответствия выборочного равнения регрессии замечаемым разрешённым может производиться и посредством средней неточности аппроксимации регрессии по формуле:
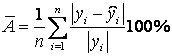
Как показывают кое-какие авторы, в практических изучениях значение данной неточности в пределах 5–7 % говорит о хорошем соответствии модели эмпирическим данным.
Коэффициент регрессии В, как уже отмечалось выше, показывает, на какое количество единиц в среднем изменяется значение показателя У, в то время, когда фактор Х возрастает на одну единицу, исходя из этого он кроме этого может служить мерой тесноты связи между Х и У. Но У зависит от единиц измерения переменных. Конкретно исходя из этого комфортно применять некую «стандартную» совокупность единиц измерения тесноты связи, в которой разные эти были бы сравнимы между собой. В качестве единиц измерения таковой совокупности употребляется среднее квадратическое отклонение переменных, а показателем тесноты связи помогает коэффициент корреляции. Величина:
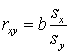
Либо

Проверка статистической значимости
в парной линейной регрессии
Проверка значимости (статистической) уравнения регрессии свидетельствует диагностику соответствия модели, высказывающей зависимость между переменными, экспериментальным данным, и диагностику достаточности включенных в уравнение растолковывающих переменных для описания зависимой переменной.
Как в любой момент, проверка статистических догадок осуществляется при некоем уровне значимости. В практических эконометрических изучениях чаще всего употребляются 5 и 1 %-ный уровни значимости. Выбор того либо иного уровня значимости определяется исследователем.
Отметим, что в случае, если нулевая догадка отклоняется при 1 %-ном уровне значимости, то она машинально отклоняется и при 5 %-ном уровне.
В случае, если нулевая догадка принимается при 5 %-ном уровне значимости, то она принимается и при 1 %-ном уровне.
В случае, если же при 5 %-ном уровне значимости нулевая догадка отклоняется, то нужно проверить ее при 1 %-ном уровне, и в случае, если наряду с этим уровне она принимается, то результаты проверки догадки приводятся для двух уровней значимости.
Правило проверки статистической значимости оценок и основывается на статистических особенностях оценок МНК и проверке статистических догадок и . Невозможность отклонения нулевой догадки свидетельствует статистическую незначимость соответствующего коэффициента и напротив, отклонение нулевой догадки если сравнивать с другой свидетельствует, что соответствующий коэффициент статистически значим.