Потому, что сопротивление Холла исчезает, исходя из этого мы имеем отношение между двумя различными сопротивлениями — сопротивлением в материальной среды и сопротивлением «пространства». В случае, если мы имеем подобный случай, мы уполномочены искать геометрию пространства, либо, иначе говоря мы не можем больше сказать о «безлюдном пространстве». От рассмотрения опыта Клицига я пришел к этим новым выводам.
Вот уравнение для узкой структурной константы:
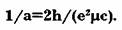
Второй вывод, что я имел возможность сделать, был связан с ответом на вопрос: по какой причине цифра 2 появляется в выражении узкой структурной константы? Да, оказалось, что цифра «два» показывает парность электронов…
…Как следствие я начал делать вывод, что у пространства должна быть структура, и что пространство должно быть квантизировано. Само собой разумеется, я думал о аналогичных идеях в более неспециализированной форме в течение долгого времени, но взор на работу фон Клицига данным образом разрешил мне объединить эти идеи новым образом и сделать кое-какие новые открытия».
Возвратимся сейчас к попыткам геометрического моделирования, проделанных Лоренцем Хехтом. С чего, фактически, начинается его размышление? С определенной констатации положения дел в данной области.
На данный момент, не смотря на то, что существует множество установленных правил для объяснения множества феноменов, зафиксированных на атомарном уровне, не существует удовлетворительной модели ядра атома. Известна достаточно созданная алгебраическая теория атома в форме квантово-механической модели, предназначенная для учета данных, собранных на базе других операций и спектрального анализа. Считается, что протоны, являясь позитивно заряженными частицами, отталкиваются друг от друга , пока между ними не появляется расстояние, начиная с которой они притягиваются до тех пор, пока не приблизятся друг к другу через чур близко, тогда они снова начинают отталкиваться.
Лоренц Хехт и Роберт Дж. Мун, пренебрегая идеей сил и принимая к сведенью принцип «мельчайшего действия», постарались расположить заряды на сфере. Наряду с этим число зарядов, существование орбитальных электронов и оболочек за границами ядра предполагает размещение в пространстве и состыковку данных сфер. Лоренц Хехт исходит из весьма несложного принципа, что Вселенная и на макро-, и на микроуровне организована одинаково. Везде должны соблюдаться однообразные гармонические пропорции, предложенные астрологом Иоганном Кеплером для упорядочения тел планет Нашей системы.
Глубокоуважаемые читатели, тут мы рекомендуем обратить особенное внимание на предложенный фрагмент текста. В нем излагается принцип, на базе которого Лоренц Хехт и Мун дальше стали выстраивать схематизации и принцип моделирования. Для осуществления моделирования они применяли пять верных платоновских тел — тетраэдр, куб, октаэдр, икосаэдр, додекаэдр (см. рис. 21 на следующей странице). Мун развил модель, основанную на соединении различных платоновских тел между собой, на их особенных сочетаниях. 92 протона конечно видящихся элементов определяются вершинами двух аналогичных пар сочлененных тел.
Напомним вам, глубокоуважаемые читатели, что такое платоновские тела. Платоновские тела являются геометрическими конструкциями, каковые превосходны тем, что организованы на базе граней, равных в каждой фигуре друг другу, выстроенных при помощи верных плоскостных фигур (равностороннего треугольника в тетраэдре, октаэдре, икосаэдре, квадрата, пятиугольника), и имеют равные углы.
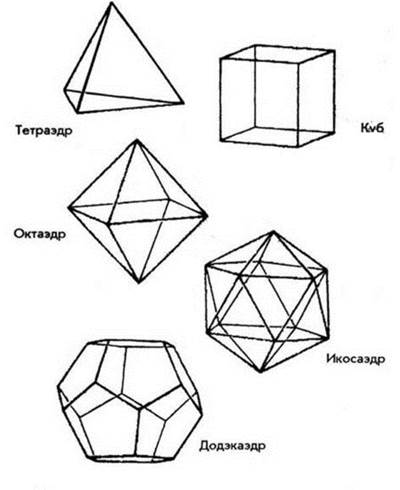
Рис. 21
Пять верных платоновских тел являются пределом конструктивности в трехмерном пространстве (см. рис 21). С позиций Хехта, это доказывается следующим образом. Все платоновские тела смогут быть выстроены на базе пересечения громадных кругов на сфере. Громадный круг есть методом мельчайшего действия на поверхности сферы, а сама сфера есть трехмерным количеством, созданным мельчайшим действием ротации. В этом, фактически, и состоит догадка группы Л. Ларуша, что платоновские тела — это не что иное, как определенного типа оестествления небольших квантов действий с веществом природы.
Из платоновских тел возможно взять так именуемые архимедовы тела (рис. 22), каковые будут не абсолютно верные, а полуправильные, — в них верные фигуры будут использованы лишь для двух либо трех граней геометрического объекта. И архимедовы, и платоновские тела смогут быть обрисованы сферой так, что все вершины тел будут касаться данной сферы.
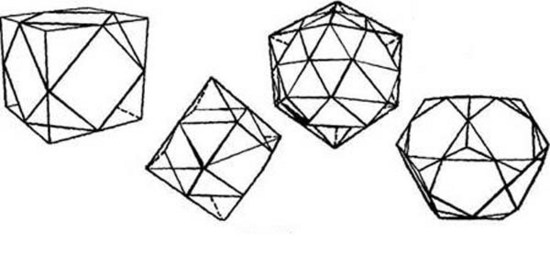
Рис. 22
Платоновские тела, в отличие от архимедовых, неповторимы, в силу того, что вовнутрь их возможно вписать лишь одну сферу, которая изнутри будет касаться каждой грани тела (см. рис. 23). Архимедовы же тела смогут иметь две либо кроме того три вписанных сферы.
И в платоновских, и в архимедовых телах существует еще так называемая срединосфера, которая строится при помощи радиуса, связывающего центр тела с серединой каждой из граней. Срединосфера проходит в платоновских телах и снаружи, и в.
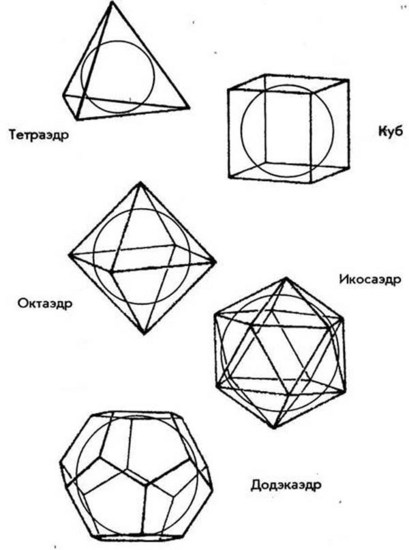
Рис. 23
В случае, если в кубе выстроить срединосферу, то мы возьмём двенадцать точек касания среди-носферы с гранями куба. Соединив эти двенадцать точек, мы возьмём архимедово тело, именуемое кубоктаэдр. Подобным образом из икосаэдра возможно получено архимедово тело — икосидодекаэдр.
Дальше Мун, создавая модель кеплеровского атома, осуществляет вкладывание разных фигур приятель в приятеля (см. рис. 24). С позиций процедуры вложения, мы приобретаем дуальные фигуры куб-октаэдр, икосаэдр-додекаэдр. Это вложение имеет следующую изюминку: вершины вкладываемой фигуры находятся посредине грани того тела, вовнутрь которого осуществляется вложение. Подобными особенностями владеет и тетраэдр по отношению к себе самому.
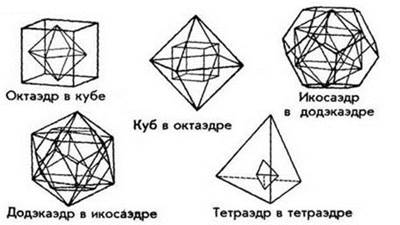
Рис. 24
Дальше появляется определенная неприятность вложения первой пары — куб-октаэдр в несколько икосаэдр-додекаэдр. Неясно, как соотнести 6 вершин октаэдра с 20 гранями икосаэдра, помимо этого, эти тела владеют различными типами симметрии, — четверная осевая симметрия октаэдра не соотносима, на первый взгляд, с пятерной осевой симметрией икосаэдра. Но, с позиций Муна и Хехта, подобное вложение выясняется вероятным.
Они его предлагают организовать так, дабы, располагая шесть вершин октаэдра неподалеку от шести вершин икосаэдра, расстояние от расположенной по близости вершины икосаэдра до противоположного ребра делилось в соответствии с Божественной пропорцией:
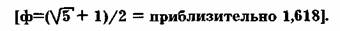
Глубокоуважаемые читатели! На этом этапе по окончании проделанных вложений возможно утверждать, что Хехт и Мун создали семиотический язык, чтобы обрисовывать отношение и взаимосвязь химических элементов. Как бы вы охарактеризовали проделанную на этом этапе работу?
Мы бы ее связали с конструированием языка. Хехтом и Муном, так, был сконструирован язык, а сейчас задача пребывает в том, дабы выстроить фактически модель.
Отличие языка от модели содержится в том, что модель обязана воображать — говорить и показывать — наиболее значимые характеристики обрисовываемого объекта. Значит, чтобы перейти от сконструированного языка к модели, нужно наложить характеристики объекта на язык.
Посмотрим, как это делают Хехт и Мун.
Лоренц Хехт предлагает отождествить вершины каждого тела с протонами, каковые по идее должны обнаруживаться в единичных точках аналогичного пространства. Сейчас, в случае, если начать выкладывать определенный комплект фигур по порядку их вложения приятель в приятеля, мы возьмём следующий последовательность:
- Кислород (8) = завершенный куб.
- Кремний (14) = завершенный октаэдр с положенным кубом (8+6).
- Железо (26) = завершенный икосаэдр с положенными кубом и октаэдром (12+6+8).
- Палладий (46) = завершенный додекаэдр с положенными прошлыми фигурами (20+12+6+8).
- Уран (92) = завершенные близнецовые тела.
Так, очень стабильный кислород, насчитывающий 62,55% всех атомов в земной коре, и кремний, составляющий 21,22%, представлены первыми двумя завершенными фигурами .
Как мы уже сообщили, закон, открытый Д.И. Менделеевым и Л. Майером, демонстрирует понятие периодичности последовательности особенностей элементов: количества (отношение массы к плотности), сжимаемости, коэффициента расширения, обоюдных точек плавления.
Лоренц Хехт обратил внимание на то, что минимальный количество имеют элементы с порядковыми номерами 4—8, 13-14, 26, 46.
С позиций Хехта, эти минимумы предполагают, что минимальное заполнение пространства и большая структурная стабильность происходят при заполнении каждого платоновского тела в пределах ядра. Модельные характеристики данного языка смогут быть показаны кроме этого при анализе феномена расщепления ядра.
В том случае, в то время, когда протонами заполняется самая внешняя фигура из вписанных приятель в приятеля платоновских тел — додекаэдр, мы приобретаем палладий. С позиций конфигурации электронов (см. рис. 25 на следующей странице), палладий есть единственным элементом, у которого внешняя электронная оболочка, предварительно занятая, абсолютно покинута электронами.
Палладий владеет следующими изюминками расщепления ядра: в таблице распределения продуктов расщепления он имеет минимальные значения. Само расщепление ядра у палладия происходит при высокой энергии (протоны с энергией нескольких миллиардов электрон/ Вольт), в то время, когда ядра расщепляются на две части однообразного размера.
В соответствии с отечественной моделью, переход к следующим элементам за палладием предполагает создание «близнецовой модели» на базе соединения гранями двух додекаэдров между собой (см. рис. 26 на следующей странице).
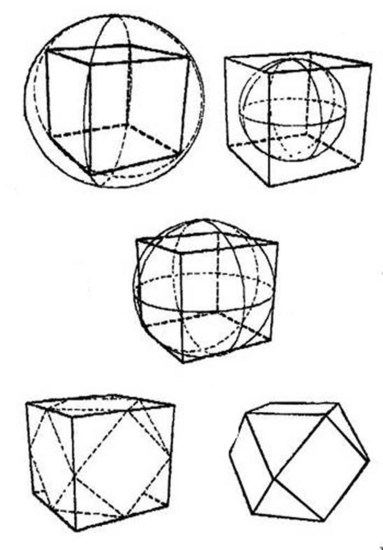
Рис. 25
В взятой модели вершины заполняются протонами начиная с самого внешнего тела, другими словами с додекаэдра При подобном соединении пять вершин оказываются недоступны, — это точки, в которых вершины грани одного додекаэдра соединяются с вершинами грани другого.
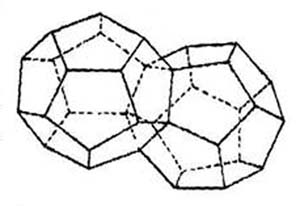
Рис. 26
Помимо этого, одна вершина вписанного вовнутрь одного из додекаэдров икосаэдра, наталкивается в середине грани додекаэдра на подобную вершину икосаэдра, вписанного в второй додекаэдр.
Так, для помещения протонов во второй «близнецовой» фигуре дешёвыми являются 15 из 20 вершин додекаэдра и 11 из 12 вершин икосаэдра. Последовательно заполняя сперва 11 вершин «близнецового» додекаэдра, мы приобретаем целый комплект элементов — от серебра с ядерным весом 47 до латания с порядковым номером 57. После этого пять вершин одной грани додекаэдра остаются незаполненными, делая вероятным заполнение внутренних фигур. Следующими заполняются октаэдр и куб, создавая 14 элементов — лантаноидов, либо серию из редкоземельных элементов (от цезия с порядковым номером 58 до лютеция с порядковым номером 71)
Помещение заряженных протонов на внутренние тела вызывает соответствующее их втягивание вовнутрь электронных орбит. С позиций Лоренца Хехта, это растолковывает процесс заполнения до этого свободных (см. табл. 1 на следующей странице) f-орбит и, тем самым, разрешает загаадку редкоземельных элементов
Таблица 1. Орбиты электронов элементов с ядерными порядковыми номерами от 1 до 54.
| Ядерный № | Элемент | К | L | M | N | О |
| s | sp | spd | spdf | spdf | ||
| Н | ||||||
| Не | ||||||
| Li | ||||||
| Be | ||||||
| В | ||||||
| С | ||||||
| N | ||||||
| О | ||||||
| F | ||||||
| Ne | ||||||
| Na | ||||||
| Mg | ||||||
| Al | ||||||
| Si | ||||||
| P | ||||||
| S | ||||||
| Cl | ||||||
| Ar | ||||||
| К | ||||||
| Ca | ||||||
| Sc | ||||||
| Ti | ||||||
| V | ||||||
| Cr | ||||||
| Mn | ||||||
| Fe | ||||||
| Co | ||||||
| Ni | ||||||
| Си | ||||||
| Zn | ||||||
| Ga | ||||||
| Ge | ||||||
| As | ||||||
| Se | ||||||
| Br | ||||||
| Kr | ||||||
| Rb | ||||||
| Si | ||||||
| V | ||||||
| Zr | ||||||
| Nb | ||||||
| Mo | ||||||
| To | ||||||
| Ru | ||||||
| Rh | ||||||
| Pd | ||||||
| Ag | ||||||
| Cd | ||||||
| In | ||||||
| Sn | ||||||
| Sb | L 23 | |||||
| Те | ||||||
| I | ||||||
| Xe |
Фигура выясняется абсолютно завершенной на радоне с ядерным числом 86 — последним инертным газом. Дабы дошагать до урана с порядковым числом 92 необходимо дать место для заполнения пространства еще шести протонам.
Для этого что-то нужно высвободить в близнеце додекаэдре в области вершины соприкасающейся грани с гранью близнеца. Для этого додекаэдры-близнецы должны применять собственные соответствующие ребра как необычную дверную петлю (см. рис. 27) и отвести друг от друга грани.
Рис. 27
В следствии у нас освобождаются как минимум че-тыре места для заполнения протонами, — три вершины на сторонах пятиугольной грани и одна вершина вписанного икосаэдра. Заполняя этих четыре вершины протонами, мы ^получаем франций, радий, актиний и торий с порядковыми номерами 87, 88, 89, 90.
Для того чтобы получить протактиний, нужно иметь еще одну вершину. Придется сломать петлю и «повесить» два додекаэдра друг на друга при помощи всего одной вершины (см рис. 28). Наконец, для получения урана и введения в воздействие еще одного протона, додекаэдры должны «соскочить» с вершины и чуть-чуть врезаться приятель в приятеля, не разрешая протонам занять одну и ту же позицию Подобная, очень нестабильная фигура может распадаться при мельчайшей провокации.
Рис. 28
Вопрос: по какой причине приходится подобным образом организовывать протоны, осуществляя сложные процедуры геометрического воображения?
В случае, если читатели уверены в том, что протоны возможно располагать произвольно, значит, у них имеется догадки определенной организации пространства и времени микромира. В частности, они уверены в том, что пространство микромира пусто, и они его смогут организовывать произвольно, как захотят. Но с этого, фактически, и появились мысли Дж. Мура о необычном трансформации сопротивляемости пространства, приведенные в начале данной главы, каковые показывают нелинейный темперамент трансформации сопротивления.
Представленное обсуждение разрешает разглядеть изменение протонных оболочек. К тому же, из выдающегося главного открытия в химии XIX века о периодичности элементов как мы знаем, что периодичность химических и физических качеств не сходится с периодичностью протонных оболочек. Последняя определяется промежутками 8, 14, 26, 46. Первая определяется последовательностью громадных периодов (18 либо 32) либо малых периодов (8). С помо-Щью спектроскопии (особого анализа спектральных линий) возможно замечать, как происходит заполнение электронных оболочек К, L, M, N, О, любая из которых содержит пол-оболочки s, р, d, f. Последовательное заполнение оболочек будет воображать собой числовые последовательности: 2, 8,8, 18, 18, 32.
Исследователь неприятностей квантовой физики Рюдберг представил эту последовательность математически:
2 х 12 = 2
2 х 22 = 8
2 х семь дней2 = 18
2 х 42 = 32
Физик Мария Гепперт-Майер, изучая свойства ядер, нашла неожиданные трансформации особенностей при определенных значениях ядерного числа (количества протонов в ядре), числа нейтронов либо массового числа (определяется как сумма нейтронов и числа протонов). Это числа 2, 8, 20, 28, 50, 82, 126. Эти числа, не имеет значение, обозначают ли они ядерное, нейтронное либо массовое число, в большинстве случаев, связаны с резким трансформацией ядерных особенностей одного какого-либо элемента если сравнивать с соседними. Это еще не правило, но определенная тенденция.
Как растолковать подобную числовую последовательность?
Лоренц Хехт сперва обращает внимание на то, что на базе определенных комбинаций данных чисел возможно приобретать число граней в платоновских телах:
8 — 2 = 6 — число ребер в тетраэдре;
20 — 8 = 12 — число ребер в кубе;
50 — 20 = 30 — число додекаэдра и рёбер икосаэдра.
Нейтроны должны иметь устойчивое определенное расположение в структуре ядра. В противном случае, как По другому возможно растолковать, по какой причине одних изотопов довольно много (у элементов с различающимся ядерным весом), а вторых совсем нет. Отметим, что изотопами именуют атомы, владеющие однообразным зарядом ядра, но различным числом нейтронов и, следовательно, различным массовым числом. Не владея зарядами, нейтроны не находятся так же симметрично, как протоны.
Думая над положением нейтронов в палладии и железе (их, соответственно, в этих элементах 30 и 60), Лоренц Хехт обратил внимание на то, что сумма общего числа граней у тетраэдра, куба и октаэдра равняется 30 (6+12+12). Хехт высказал предположение, что нейтроны смогут размешаться на ребрах фигур, а не на их вершинах, где находятся протоны. Наряду с этим появляется возможность вписывать одни фигуры в другие. Так, к примеру, тетраэдр возможно вписан в куб так, что середина ребер тетраэдра лежит в центре каждой из граней куба. Вовнутрь тетраэдра возможно вписан еще один тетраэдр. В случае, если соединить середины граней разных фигур между собой, то мы, соответственно, возьмём кубоктаэдр из куба либо октаэдра и икосидодэкаэдр из икосаэдра либо соответственно додекаэдра.
Главная мысль Лоренца Хехта пребывает в следующем: в то время, когда заполняется протоновая оболочка, мы имеем самое стабильное состояние ядра, что отражается в огромном количестве элементов данного типа, потому, что с завершением нейтронной оболочки мы имеем завершение периода периодической совокупности.
Структура гелия возможно представлена как тетраэдр, содержащий два протона и два нейтрона в четырех вершинах. С переходом к литию — третьему элементу периодической совокупности — протоны движутся во вне, начиная строить собственную первую оболочку в вершинах куба. Двум нейтронам никуда перемещаться не нужно, и они остаются на вершинах тетраэдра. С возникновением новых нейтронов они находятся в центре граней куба либо, что то же самое, на середине ребер большего тетраэдра, образованного всеми диагоналями граней куба. Меньший тетраэдр возможно назван альфа частицей.
Для того чтобы выяснить, как устроена эта модель, нужно представить себе, как один тетраэдр вписан в второй — меньший, дуальный тетраэдр, что воображает и символизирует альфа-частицу, имеет ребро величиной в одну треть от ребра «родительского» громадного тетраэдра, и, как тетраэдр вписан в куб (см рис. 29).
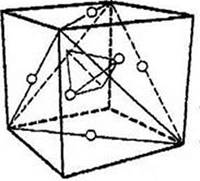
Рис. 29
Любой куб предполагает тетраэдр. Четыре диагонально противоположных вершины куба совпадают с четырьмя вершинами тетраэдра. Шесть ребер тетраэдра формируют диагонали граней куба, и середина ребер сходится с центром граней.
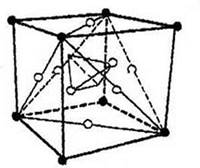
Рис. 30
В случае, если разглядеть углерод (шестой номер в периодической совокупности с массовым номером 12), то его два нейтрона находятся в альфа частице — в вершинах меньшего тетраэдра, а четыре вторых нейтрона — на гранях куба (см рис. 30).
В случае, если мы разглядим кислород, то, не считая двух нейтронов, расположенных в вершинах меньшего тетраэдра, другие шесть нейтронов заполняют все грани куба (см. рис 31). Шесть протонов находятся в вершинах куба. Так, у кислорода закончены как протонная, так и нейтронная оболочки
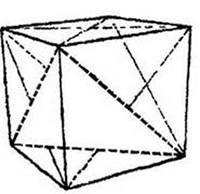
Рис. 31
В случае, если мы перейдем к концу этого последовательности в периодической совокупности — к элементу неону, — у нас имеется лишь одна возможность для размещения двух нейтронов оставшиеся две свободные вершины внутреннего малого тетраэдра. Та же обстановка повторяется для криптона и аргона».
Глубокоуважаемые читатели! На этом мы завергиим рассмотрение весьма увлекательной работы, Лоренца Хехта и попросим вас выполнить следующие задания. Как бы вы имели возможность схематизировать его работу, ответив на вопрос: а что он, фактически, делает? Мы согласимся вам, что структура схематизма появляется, в первую очередь, из попыток ответить на вопросы: что человек делает? Как он выстраивает собственную работу?
Второй важный вопрос пребывает в том, дабы Заметить, сколько всего различных языков применяет Лоренц Хехт в собственной работе и как использует любой из этих языков. Как он, фактически, собирает, объединяет либо разделяет эти языки? Анализ того, сколько языков он комбинирует и соединяет, как он их сочленяет, окажет помощь нам детальнее разобраться с тем, как Хехт выстраивает собственный представление об изучаемом объекте.
В первую очередь, мы сходу выделили бы следующие четыре языка:
- геометрическийязык, в котором исследователь старается соединять различные представления. Это необычный язык монтажа — в нем, в большинстве случаев, должны быть соединены и синтезированы другие языки;
- нумерологический,либо арифметический язык, что упорядочивает в структуре чисел чёрта химических элементов;
- химическийязык, что обрисовывает иногда изменяющиеся свойства и закономерности этих элементов;
- физическийязык, что обрисовывает физические особенности перечисленных элементов.
Отдельный вопрос, для нас очень важный, содержится в том, что геометрический язык употребляется Лоренцем Хехтом, как минимум, в двух совсем различных функциях. С одной стороны, — это монтажная оболочка, в которой должны быть собраны и переинтерпретированывсе другие языки. Но, иначе, у данного языка имеется и собственная функция — заметить конечную геометрическую конструкцию либо последовательный последовательность развертываемых конструкций, каковые разрешают растолковать все сущностные, наиболее значимые характеристики химических элементов.
Появляется вопрос: а на чем, где и как может осуществляться подобная работа? Как эту работу делать по определенным твёрдым правилам, как следует, а не только бы от нее отделаться?
Эта работа осуществляется на верстаке семиотического конструирования. Подобное суперсредство схематизации было предложено Г.П. Щедровицким, на котором он разбирал и демонстрировал создания новых и способ порождения знаково-семиотических конструкций.
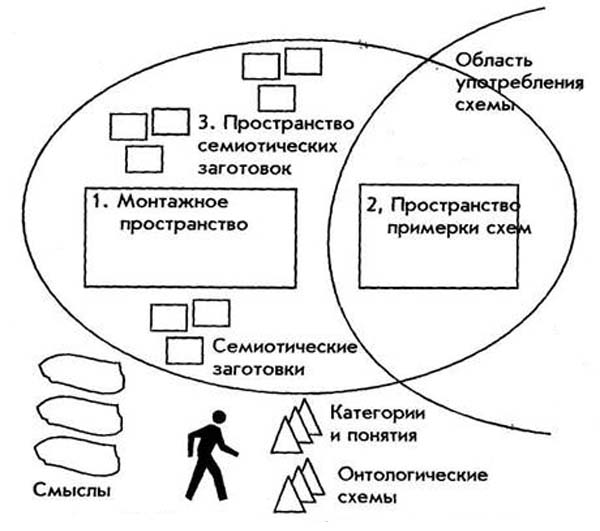
Рис. 32. Устройство семиоического верстака
(Вариант устройства предложен С.П. Усольцевым)
Каково же устройство верстака и как он трудится?
Во-первых, на самом верстаке весьма четко выделяется монтажное пространство — 1. Это то самое пространство, в котором осуществляется семиотическая работа по созданию и построению новой схемы либо семиотической конструкции. Конкретно в этом месте схематизатор либо семиотик осуществляет конструктивно-семиотическую работу, создавая новую схему.
Весьма четко выделяется вторая отдельная часть на верстаке семиотического конструирования — 2. В том направлении помещается уже практически завершенная заготовка. Тут созданная конструкция примеривается и прилаживается к грядущей работе: анализируется, как она отправится в дело, как будет жить собственной судьбой.
Будучи опробована в этом примерочном пространстве, она возвращается назад для шлифовки и окончательной доработки.
Справа от верстака расположен особенный участок, где находятся средства, используемые для построения схемы либо семиотической конструкции. Это, как бы, амбар либо арсенал. Что есть подобными средствами, каковые используются при построении конструкций и схем из знаков? В первую очередь, это понятия и категории, определяющие главные расчленения форм и объекта организации действия, каковые находят собственный отражение на схеме.
Во-вторых, это определенные онтологические схемы объекта, на которых демонстрируются сущностное устройство объекта и его модельные характеристики.
Время от времени на верстак из арсенала смогут доставляться еще незаконченные конструкции, каковые употреблялись для ответа вторых задач, но тут они приобретают новое назначение и употребляются по-новому. Они втягиваются в особенное пространство, окружающее верстак, — 3. Это инструменты, забранные из арсенала и включенные в рабочий процесс.
Под верстаком расположен материал, что используется для осуществления схематизации. В качестве этого материала, в первую очередь, выступают разные смыслы, результаты понимания некоторых черт объекта либо ситуации. То выстраивая конструкцию, то сбрасывая ее вниз, в существующее поле работ, мы любой раз примеряем, быть может ли она сейчас употребляться, начнет ли она жить без нас и кроме нас, собственной судьбой.