а)Способами отыскания экстремумов многоэкстремальных функций;
b) Способами отыскания лишь минимумов многоэкстремальных функций;
c) Способами отыскания экстремумов унимодальных функций;
d) Способами отыскания лишь максимумов многоэкстремальных функций;
e) Способами отыскания лишь минимумов унимодальных функций.
Верный ответ е
Оптимизационную задачу относят к линейному программированию, в случае, если
а) функции ограничений и целевая функция линейны;
b) целевая функция вогнута, а функции ограничений образуют выпуклое множество;
c) целевая функция линейна, а функции ограничений образуют выпуклое множество;
d) целевая функция вогнута, а функции ограничений линейны;
e) целевая функция вогнута и нет ограничений.
Верный ответ а
24.Имеется транспортная таблица
| А | ||||
При каком значении параметра А задача есть задачей закрытого типа?
А) А=30 Б) А=40 В) А=50 Г) А=60 Д) А=70
Верный ответ: г
25.Имеется симплекс таблица
| -3 | ||||
| Б | b | X1 | X2 | X3 |
В первой строке базовой переменной есть
А) X1 Б) X2 В) X3
Верный ответ: б
Раздел 4
Целевая функция – это
a)каждая функция, у которой имеется экстремумы
b)каждая функция, у которой нет экстремумов;
c) каждая функция, у которой имеется минимумы;
d) функция, экстремумы которой нужно отыскать;
e) каждая функция, у которой имеется максимумы.
Верный ответ a
2.Оптимизация совокупности состоит
a) в поиске таковой совокупности, в которой максимум параметров управления;
b) в поиске для того чтобы комплекта параметров управления, при котором целевая функция достигает экстремума;
c) в поиске для того чтобы комплекта параметров управления, при котором целевая функция самый оптимальна;
d) в поиске для того чтобы комплекта параметров управления, при котором целевая функция самая оптимальная;
e) в поиске минимального комплекта параметров управления, при которых целевая функция достигает экстремума.
Верный ответ b
3.В каких из перечисленных случаев задача отыскания экстремума функционала может не иметь решения
а) в то время, когда подынтегральная функция не зависит от y’.
б) в то время, когда подынтегральная функция линейно зависит от y’.
в) в то время, когда подынтегральная функция зависит лишь от y’.
г) в то время, когда подынтегральная функция зависит лишь от y и y’.
Верный ответ a
Раздел 5
4.Уравнение Эйлера, к которому сводится задача отыскания экстремалей интегрального функционала с подынтегральной функцией , в общем случае есть:
а) обычным дифференциальным уравнением второго порядка.
б) обычным дифференциальным уравнением первого порядка
в) трансцендентным алгебраическим уравнением.
Верный ответ a
5.Какие конкретно из перечисленных утверждений верны:
а) матрица Гессе симметрическая.
б) матрица Гессе диагональная.
в) определитель матрицы Гессе не может быть равен нулю.
Верный ответ а
6.Какое число неизвестных множителей Лагранжа возможно в задаче условной оптимизации, в случае, если число переменных в составе оптимизируемой функции равняется 8.
а) не более 7
б) не более 8
в) любое количество
Верный ответ в
7.Для решения задачи условной оптимизации способом неизвестных множителей Лагранжа непременно:
а) знание аналитического выражения оптимизируемой функции.
б) наличие ограничений лишь в виде равенств.
в) линейность ограничений.
Верный ответ а
8.В случае, если в критической точке функции одной переменной вторая производная отрицательна, то:
а) эта точка есть точкой максимума.
б) эта точка есть точкой минимума.
в) в данной точке функция имеет разрыв.
Верный ответ а
9.Какая точка в способе Хука–Дживса именуется временной вершиной?
а) точка, в которой достигается наилучшее значение функции отклика по окончании пробных шагов по всем факторным переменным из некоей базисной точки.
б) каждая точка, в которой в ходе поиска определяется значение функции отклика.
в) точка, в которой достигается громаднейшее изменение функции отклика если сравнивать с предшествующей.
Верный ответ а
10.В то время, когда употребляются неградиентные способы оптимизации функций многих переменных.
а) в то время, когда неизвестно аналитическое выражение функции отклика, либо ее производные не смогут быть отысканы.
б) в случае, если функция отклика строго выпукла либо строго вогнута.
в) в то время, когда функция отклика имеет овражную структуру.
Верный ответ а
11.Требуется ли вычисление градиента функции отклика для реализации оптимизационной процедуры способа Хука–Дживса?
а) нет.
б) требуется в базисных точках.
в) требуется во временных вершинах.
Верный ответ а
12.Какой способ самый действен для отыскания глобального экстремума произвольной неунимодальной функции отклика.
а) способ сканирования.
б) способ наискорейшего подъема.
в) симплекс-способ.
Верный ответ а
13.Какое число вершин имеет верный симплекс в пространстве, размерность которого равна 17?
а) 18;
б) 17;
в) 16.
14.При реализации способа барьерных функций последовательность чисел {rk} формируется как:
а) убывающая.
б) убывающая, члены которой образуют сходящийся числовой последовательность.
в) возрастающая.
Верный ответ б
15.Чему делается равна барьерная функция I(x) при попадании на границу множества допустимых значений?
а) I(x) = 0
б) I(x) = ?
в) I(x) 0
Верный ответ б
16.При построении штрафных функций F(x,rk) последовательность чисел {rk} формируется как:
а) возрастающая.
б) убывающая.
в) убывающая, члены которой образуют сходящийся числовой последовательность.
Верный ответ в
Раздел 6
17.В случае, если при реализации способа проекции градиента на k-ом шаге в точке xk направление градиента функции отклика сходится с направлением нормали к поверхности, ограничивающей область допустимых значений переменных, то:
а) точка xk есть точкой оптимума.
б) координаты точки xk выяснены неверно.
в) протяженность шага из точки xk должна быть удвоена.
Верный ответ а
18.Отыскать четырнадцатое число F14 в последовательности чисел Фибоначчи.
а) 610.
б) 377;
в) 233;
Верный ответ а
19.Промежутком неопределенности именуется:
а) промежуток, точно содержащий точку максимума (минимума) исследуемой функции.
б) произвольный промежуток, протяженность которого совершенно верно малоизвестна.
в) промежуток, в которого находятся все критические точки исследуемой функции.
Верный ответ а
20.Чему будет равна протяженность промежутка неопределенности при применении способа золотого сечения, в случае, если реализовано 9 замеров, а протяженность исходного промежутка равна 14?
а) ~0,298;
б) 0,184;
в) ~0,482.
Верный ответ а
21.В каких точках промежутка [0,12] направляться выполнить измерения для отыскания экстремума унимодальной функции в соответствии с минимаксной стратегией пассивного поиска по 5 точкам?
а) в точках 2; 4; 6; 8; 10.
б) в точках 0; 3; 6; 9; 12.
в) в произвольных пяти точках, выбранных на заданном промежутке случайным образом.
Верный ответ б
Способы Чисел Фибоначчи и Золотого сечения являются
а)Способами отыскания экстремумов многоэкстремальных функций;
b) Способами отыскания лишь минимумов многоэкстремальных функций;
c) Способами отыскания экстремумов унимодальных функций;
d) Способами отыскания лишь максимумов многоэкстремальных функций;
e) Способами отыскания лишь минимумов унимодальных функций.
Верный ответ е
Оптимизационную задачу относят к линейному программированию, в случае, если
а) функции ограничений и целевая функция линейны;
b) целевая функция вогнута, а функции ограничений образуют выпуклое множество;
c) целевая функция линейна, а функции ограничений образуют выпуклое множество;
d) целевая функция вогнута, а функции ограничений линейны;
e) целевая функция вогнута и нет ограничений.
Верный ответ а
24.Имеется транспортная таблица
| А | ||||
При каком значении параметра А задача есть задачей закрытого типа?
А) А=30 Б) А=40 В) А=50 Г) А=60 Д) А=70
Верный ответ: в
25.Имеется симплекс таблица
| -3 | ||||
| Б | b | X1 | X2 | X3 |
В первой строке базовой переменной есть
А) X1 Б) X2 В) X3
Верный ответ: а
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ (ЭКЗАМЕНУ) ПО ДИСЦИПЛИНЕ
1. Что такое инструментальные переменные и параметры математической модели? В чем состоит их отличие?
2. Что такое допустимое множество?
3. Что такое целевая функция и критерий оптимизации?
4. Что такое линии уровня целевой функции?
5. Дайте формулировку детерминированной статической задачи оптимизации.
6. Назовите обстоятельства неопределенности в параметрах математической модели и объясните ее влияние на решение.
7. Приведите примеры применения математических моделей для описания поведения экономических агентов.
8. Что такое рациональное поведение с позиций теории оптимизации?
9. Как способы оптимизации употребляются при принятии экономических ответов?
10. Поведайте об применении оптимизации в задачах идентификации параметров математических моделей.
11. Что такое глобальный оптимальное решение и максимум критерия?
12. Достаточное условие существования глобального максимума (теорема Вейерштрасса).
13. Назовите обстоятельства отсутствия оптимального ответа.
14. Что такое локальный максимум?
Тема II
15. Сформулируйте неспециализированную задачу нелинейного программирования.
16. Сформулируйте нужное условие локального максимума в общей задаче нелинейного программирования.
17. Что такое функция Лагранжа?
18. Дайте определение седловой точки функции Лагранжа.
19. Сформулируйте и докажите достаточное условие оптимальности посредством функции Лагранжа.
20. Сформулируйте условие дополняющей нежесткости и дайте его экономическую интерпретацию.
21. Дайте определение выпуклого множества.
22. Какие конкретно особенности имеют выпуклые множества?
23. Дайте определение опорной гиперплоскости.
24. Дайте определение разделяющей гиперплоскости.
25. Сформулируйте и проиллюстрируйте теорему об отделимости выпуклых множеств.
26. Сформулируйте понятие выпуклой и вогнутой функций.
27. Что такое строгая выпуклость функции?
28. Что такое надграфик функции? Какими особенностями владеет надграфик выпуклой функции?
29. Сформулируйте достаточное условие выпуклости функции.
30. Какие конкретно особенности имеют выпуклые функции?
31. Сформулируйте выпуклую задачу нелинейного программирования.
32. Сформулируйте теорему о глобальном максимуме в выпуклом случае.
33. Приведите содержательный пример выпуклой задачи нелинейного программирования.
34. Сформулируйте теорему Куна-Таккера.
35. Дайте экономическую интерпретацию множителей Лагранжа.
36. Как решения выпуклой задачи оптимизации зависят от параметров?
Тема III
37. Сформулируйте задачу линейного программирования.
38. Приведите содержательные примеры задачи линейного программирования.
39. Что такое обычная (стандартная) и каноническая формы задачи линейного программирования?
40. Какие конкретно свойства имеет допустимое множество задачи линейного программирования?
41. Какие конкретно свойства имеет оптимальное ответ в задаче линейного программирования?
42. Как выглядят функция Лагранжа и условия Куна-Таккера в задаче линейного программирования?
43. Сформулируйте двойственную задачу линейного программирования.
44. Сформулируйте теоремы двойственности в задаче линейного программирования.
45. Дайте интерпретацию двойственных переменных в задаче линейного программирования.
46. Поведайте об анализе чувствительности в задаче линейного программирования.
47. Примените графический способ для ответа конкретной задачи линейного программирования.
48. В чем состоят способы ответа задач линейного программирования, основанные на направленном переборе вершин (симплекс-способ и др.)?
49. Какие конкретно возможности предоставляет среда MS Excel для ответа задач линейного программирования?
50. В чем состоят градиентные способы ответа задачи абсолютной оптимизации?
51. Как штрафные функции употребляются при поиске ответа выпуклой задачи нелинейного программирования?
52. Поведайте о способах ответа задач линейного программирования, основанных на применении штрафных функций.
Тема IV
53. Сформулируйте задачу выбора ответов в условиях неопределенности.
54. Назовите и сформулируйте критерии выбора ответов в условиях неопределенности (принцип гарантированного результата, критерий Гурвица, критерий Байеса-Лапласа, критерий Сэвиджа).
55. Как определяется множество допустимых обеспечивающих программ?
56. Что такое наилучшая обеспечивающая программа?
57. Как употребляется вероятностная информация о параметрах в задачах принятия ответов при случайных параметрах.
58. В чем состоит принятие ответов на базе математического ожидания?
59. Как учитывается склонность к риску?
Тема V
60. Сформулируйте постановку задачи многокритериальной оптимизации.
61. Что такое множество достижимых критериальных векторов?
62. Дайте оптимальности и определение доминирования по Парето.
63. Что такое действенные ответы и паретова граница.
64. Назовите главные подходы к построению способов поиска ответов в задачах многокритериальной оптимизации.
Тема VI
65. Приведите примеры многошаговых совокупностей в экономике.
66. В чем состоят изюминке динамических задач оптимизации?
67. Приведите примеры динамической задачи оптимизации.
68. Что такое многошаговые динамические модели?
69. Что такое постоянные динамические модели?
70. Что такое переменная состояния и управление в динамических моделях?
71. Приведите примеры задания критерия в динамических задачах оптимизации.
72. В чем состоит способ динамического программирования в многошаговых задачах оптимизации?
73. Сформулируйте принцип оптимальности и запишите уравнение Беллмана.
74. Как задача оптимизации многошаговой совокупности сводится к задаче математического программирования?
Билеты к экзамену по курсу
« Способы оптимальных ответов »
Билет 1.
1. Определение функций многих переменных. Область определения.
2. Задача. Отыскать оптимальную цену билета на метро, в случае, если как мы знаем, что спрос на билет зависит от цены как ex.
Билет 2.
- Дифференциал функции одной и нескольких переменных.
- Задача. Решить вариационную задачу о громаднейшей площади плоской фигуры при постоянном периметре.
Билет 3.
- Частные дифференцируемость и производные функций многих переменных.
- Задача. Решить задачу линейного программирования.
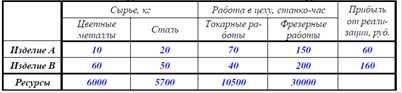
Научно-производственное объединение «Стрела» занимается изготовлением
комплектующих изделий для фирм ВПК. При изготовлении изделий типа A и типа B употребляются цветные металлы и сталь. Технологический процесс кроме этого включает обработку изделий на фрезерных станках и токарных. По технологическим нормам на производство одного изделия типа A и одного изделия типа B требуется определенное некоторый объём и количество сырья станко-часов для обработки на станках в цеху. Технологические эти производственного процесса приведены в таблице ниже. В течение месяца цеха НПО «Стрела» располагает ограниченными ресурсами по сырью и по времени работы в производственных цехах (см. таблицу). Прибыль от реализации одного изделия типа A образовывает 60 руб., а от единицы изделия типа B ? 160 руб. Отыскать оптимальный замысел производства для НПО «Стрела»
(количество изделий типа A и типа B), дающий громаднейшую прибыль.
Билет 4.
1. Производная по выделенному направлению. его свойства и Градиент.
2. Изучить на экстремум функцию двух вещественных переменных:
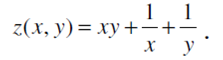
Билет 5.
- Изолинии и градиент.
- Изучить на условный экстремум функцию двух вещественных изменений-
ных
при наличии уравнения связи
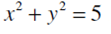
Билет 6.
1. Частные производные высших порядков.
2. Даны зависимости спроса D и предложения S от цены р. Отыщите равновес-
ную цену, выручку при равновесной цене. Отыщите цену, при которой вы-
ручка велика, и саму эту большую выручку.
Эти: D = 800 ? 20 р , S = 90 + 40 р .
Билет 7.
- их классификация и Экстремумы. Локальные и глобальные экстремумы.
- Изучить на экстремум функцию двух вещественных переменных:
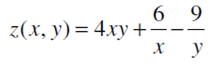
Билет 8.
1. Нужные условия существования локального экстремума функции многих пе-
ременных.
2. Изучить функцию одной переменной и выстроить ее график.
y = 3x/(x2 – 4)
Билет 9.
1. Матрица вторых частных производных и достаточные условия существования экстремума функции z = F(x,y).
2. Задача. Научно-производственное объединение «Стрела» занимается изготовлением
комплектующих изделий для фирм ВПК. При изготовлении изделий типа A и ти-
па B употребляются цветные металлы и сталь. Технологический процесс кроме этого включает
обработку изделий на фрезерных станках и токарных. По технологическим нормам на
производство одного изделия типа A и одного изделия типа B требуется определенное
некоторый объём и количество сырья станко-часов для обработки на станках в цеху.
Технологические эти производственного процесса приведены в таблице ниже.
В течение месяца цеха НПО «Стрела» располагает ограниченными ресурсами по сырью и
по времени работы в производственных цехах (см. таблицу). Прибыль от реализации од-
ного изделия типа A образовывает 70 руб., а от единицы изделия типа B ? 180 руб.
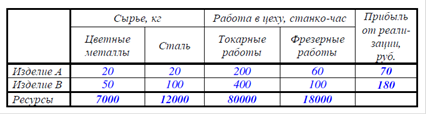
Отыскать оптимальный замысел производства для НПО «Стрела» (количество изделий типа A и
типа B), дающий громаднейшую прибыль.
Билет 10.
- Квадратичные формы. Критерий Сильвестра.
- Задача . Научно-производственное объединение «Стрела» занимается изготовлением комплектующих изделий для фирм ВПК. При изготовлении изделий типа A и типа B употребляются цветные металлы и сталь. Технологический процесс кроме этого включает обработку изделий на фрезерных станках и токарных. По технологическим нормам на производство одного изделия типа A и одного изделия типа B требуется определенное некоторый объём и количество сырья станко-часов для обработки на станках в цеху.
Технологические эти производственного процесса приведены в таблице ниже.
В течение месяца цеха НПО «Стрела» располагает ограниченными ресурсами по сырью и
по времени работы в производственных цехах (см. таблицу). Прибыль от реализации од-
ного изделия типа A образовывает 100 руб., а от единицы изделия типа B ? 250 руб.
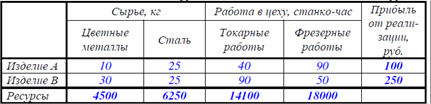
Отыскать оптимальный замысел производства для НПО «Стрела» (количество изделий типа A и
типа B), дающий громаднейшую прибыль.
Билет 11.
1. Условный экстремум. Число свободных переменных при наличии связей. Способ
Множителей Лагранжа.
2.Задача о брахистохроне.
http://vi.horizalru.com/12.html
http://www.phys.spbu.ru/content/old-pdf/File/Library/studentlectures/Budylin/var.pdf
Билет 12.
- Неспециализированная задача линейного программирования.
- Совершить полное изучение функции и выстроить ее график y = ex/x
Билет 13.
- Примеры задач линейного программирования.
- Совершить полное изучение функции и выстроить ее график y = x4-4×3+6×2-4x+1
Билет 14.
- Транспортная задача в общем виде. Постановка задачи.
- Совершить полное изучение функции и выстроить ее график
Y = (x2+1)/x
Билет 15.
- Транспортная задача. Опорный замысел. Способ северо-западного угла.
- Совершить полное изучение функции и выстроить ее график
Y = x3 + x4/4
Билет 16.
1. Графический способ ответа задачи линейного программирования.
2. Совершить полное изучение функции и выстроить ее график
Y = x- 2arctg (x)
Билет 17.
- Симплекс-способ ответа задач линейного программирования и его метод.
- Совершить полное изучение функции и выстроить ее график
Y = (8×2 – x4)1/2
Билет 18.
- Неспециализированная задача вариационного исчисления. Примеры задач вариационного исчисления.
- Отыскать экстремали в вариационной задаче, применяя частные случаи интегрируемости уравнения Эйлера:
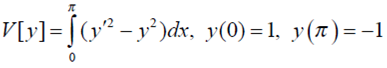
Билет 19.
- Уравнение Эйлера-Лагранжа.
- Даны зависимости спроса D и предложения S от цены р. Отыщите равняется-
весную цену, выручку при равновесной цене. Отыщите цену, при которой
выручка велика, и саму эту большую выручку. Эти:
D = 800 ? 40 р, S = 90 + 10 р .
Билет 20.
- Частные случаи уравнения Эйлера –Лагранжа в особом виде.
- Отыскать экстремали в вариационной задаче, применяя частные случаи интегрируемости уравнения Эйлера:
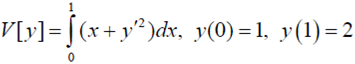
Билет 21.
1. Примеры ответа уравнения Эйлера-Лагранжа в экономических задачах.
2. Отыскать экстремаль функционала в вариационной задаче:
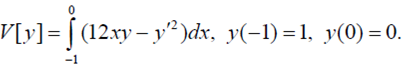
Билет 22.
1. Модель Леонтьева многоотраслевой экономики.
2. Отыскать экстремали функционала и растолковать геометрический суть задачи.
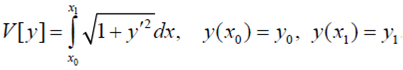
Билет 23.
1. Открытая и замкнутая модели Леонтьева.
2. Изучить на экстремум функцию двух вещественных переменных:
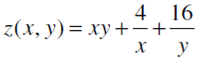
Билет 24.
- Одномерная оптимизация. Изучение функции одной переменной и нахождение ее экстремумов.
- Совершить полное изучение функции и выстроить ее график y = x2e-x
УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ
Главная литература
1. Юдин Д. Б.. Задачи и способы линейного программирования. Задачи транспортного типа. – М.: Либроком, 2010. – 184 с.
2. Соколов А. В., Токарев В. В. Способы оптимальных ответов. В 2 т. — 2-е изд., испр. — М.: ФИЗМАТЛИТ, 2011. — 564 с.
3. Афанасьев М. Ю., Багриновский К. А., Матюшок В. М.
Дополнительная литература
1.Иванилов Ю.П., Лотов А.В. Математические модели в экономике. М.: Наука, 1979.
2.Лотов А.В. Введение в экономико-математическое моделирование. М.: Издательство «Наука», 1984.
3.Хазанова Л.Э. Математические способы в экономике. Учебное пособие. М.: Изд. БЕК, 2002.
4.Васильев Ф.П. Способы оптимизации. М.: Издательство «Факториал», 2001.
5. Васильев Ф.П. Численные способы ответа экстремальных задач. М.: Наука, 1988.
6. направляться Р., Кириллова Ф.М. Способы оптимизации. Минск: Изд. БГУ, 1975.
Моисеев Н.Н., Иванилов Ю.П., Столярова Е.Н. Способы оптимизации. М.: Наука, 1978.
Токарев В.В., Соколов А.В. Способы оптимальных ответов (ридер).
Красс М.С., Чупрынов Б.П. Базы ее приложения и математики в экономическом образовании. М.: Изд. ДЕЛО, 2003.
Поляк Б.Т. Введение в оптимизацию. М.: Наука, 1983.
Fletcher R. (2000) Practical methods of Optimization. Wiley.
Rardin R.L. (1997) Optimization in Operations Research. Prentice Hall.
Walsey L.A. (1998) Integer Programming. Wiley.
14. Райфа Г. Анализ ответов. М.: Наука, 1977.
15. Clemen, R.T. (1996) Making Hard Decisions. Belmont: Duxbury Press.
Ларичев О.И. методы и Теория принятия ответов. М.: Логос, 2000.
Подиновский В.В., Ногин В.Д. Парето-оптимальные ответы многокритериальных задач. М.: Наука, 1982.
Штойер Р. Многокритериальная оптимизация: теория, приложения и вычисления. М.: Радио и сообщение, 1992.
Lotov A.V., Bushenkov V.A., and Kamenev G.K. (2004) Interactive Decision Maps. Approximation and Visualization of Pareto Frontier. Kluwer Academic Publishers.
Miettinen K. (1999) Nonlinear multi-objective optimization. Kluwer Academic Publishers.
Беллман Р., Калаба Р. современная теория и Динамическое программирование управления. М.: Наука, 1969.
Благодатских В.И. Введение в оптимальное управление. М.: Верховная школа, 2001.
Габасов Р., Кириллова Ф.М. Способы оптимизации. Минск: Изд. БГУ, 1975.
Пропой А.И. Элементы теории оптимальных дискретных процессов. М.: Наука, 1973.
Kamien, M.I., Schwarz, N.L. (1981) Dynamic optimization. The calculus of variations and optimal control in economics and management. New York: Elsevier.
Bryson A.E. (2002) Applied linear optimal control: examples and algorithms. Cambridge Univ. Press.
Denardo E.V. (2003) Dynamic Programming: Models and Applications. Dover Publ.