В хороших психофизических способах, не смотря на то, что и изучаются сенсорные свойства наблюдателя, не ставится вопрос о возможности обнаружения стимула, а учитывается только возможность ответов испытуемого “Да” (слышу либо вижу). Но легко себе представить такую обстановку, в то время, когда испытуемый, пребывав в ситуации тестирования (экспертизы), захочет продемонстрировать максимум собственных сенсорных свойств, и будет давать ответ “Да” практически в каждой пробе. Конечно, что при таких условиях количество положительных ответов не будет какое количество-нибудь совершенно верно отражать его предельные сенсорные свойства. Надежда психолога-специалиста на честность испытуемого, по-видимому, не наилучшее средство для обеспечения надежности проводимых измерений. Так, достаточно разумеется, что итог пороговых измерений может очень сильно зависеть от стратегии испытуемого давать ответы определенного рода, и, следовательно, появляется задача прямого учета поведения наблюдателя в ситуации принятия ответа об обнаружении либо различении сигнала.
Новая методика, именуемая психофизической теорией обнаружения сигнала (Green, Swets, 1966), содержит в себе представление о наблюдателе как не о пассивном приемнике стимульной информации, но как об активном субъекте принятия ответа в ситуации неопределенности.
Кратко данный подход возможно охарактеризовать следующим образом. В стимульном потоке выделяется та его часть, на которую указанием ее пространственной и/либо временной области либо ее характерного паттерна обращается внимание наблюдателя. Эта выделенная часть именуется стимулом либо предъявлением (стимула). Выделяется некий физический показатель (свойство, черта стимульного потока), что может находиться в одних пробах — значащий либо сигнальный стимул, и отсутствовать в других — безлюдный стимул. Наблюдатель, от которого требуется обнаруживать данный показатель, решает задачу двоичной классификации: относит каждое предъявление к одному из двух классов — “Нет показателя”, “Имеется показатель”. Эта задача решается методом установления схемы соответствия (которая именуется кроме этого правилом принятия ответа) между изюминками сенсорного образа предъявляемого стимула и выбираемым ответом. Эта схема соответствия может корректироваться под влиянием как предварительного информирования наблюдателя о частоте сигнальных либо безлюдных стимулов в последующих предъявлениях, так и обратной связи — оценки правильности принимаемых наблюдателем ответов.
В следующих трех разделах будут обрисованы три хороших способа обнаружения сигналов: способ “Да-Нет”, двухальтернативный метод оценки и вынужденный выбор уверенности.
§ 2. Способ “Да-Нет”
В этом способе употребляются два стимула: один значащий — , и второй пустой — . Предъявления следуют приятель за втором обыкновенно через более либо менее регулярные промежутки времени и по окончании каждого предъявления испытуемый отвечает “Да”, в случае, если был сигнал, либо “Нет”, если он не нашёл сигнала. Предъявление стимулов абсолютно рандомизировано, т.е. каждое очередное предъявление независимо от прошлых может возможно с некоей возможностью P(S) сигнальным (и, следовательно, с возможностью P(N) = 1 — P(S) — безлюдным); P(S) и P(N) сохранятся постоянными в течении всей серии предъявлений. Так, в случае, если неспециализированное число предъявлений N в опыте велико, то число сигнальных и безлюдных предъявлений примерно равняется, соответственно N•P(S) и N•P(N) (разумеется, N•P( S) + N•P(N) = N).
Разглядим сейчас вероятные комбинации , каковые смогут встретиться в опыте. Их четыре: , , , , причем первые два сочетания являются верными, два последние — ошибочными финалами. Каждое их этих сочетаний имеет собственный особое наименование, как это продемонстрировано в табл. 1.
Таблица 1
Финалы опыта по обнаружению сигнала
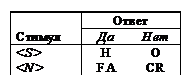 |
ложная тревога и Попадание будут в будущем обозначаться через H (от британского hit) и FA (от британского false alarm). Обозначения для правильных отрицаний и пропусков — O (omission) и CR (correct rejection). Пускай мы пересчитали количество сочетаний каждого типа: n (H), n (FA), n (O), n (CR). Разумеется, что:
n(H) + n(O) = N•P(S) , (1)
n(FA) + n(CR) = N•P(N) . (2)
Зная эти качества и нормировав каждое из них по N (т.е. поделив на общее число предъявленных проб), мы возьмём статистические оценки возможностей появления финалов каждого типа:
P(H) = n(H)/N, P(O) = n(направляться)/N, … и т.д. (3)
Но такие возможности еще не говорят нам прямо о способности наблюдателя обнаруживать сигнал. Вправду, величина p(H) зависит не только от того, как довольно часто наблюдатель идентифицирует как сигнал, но и от того, сколь довольно часто предъявлялось в опыте . Исходя из этого, дабы охарактеризовать деятельность испытуемого в данном опыте, отделив ее от деятельности экспериментатора (решающего, в частности, сколько раз предъявить , а какое количество — ), принято воображать результаты опыта в виде оценок условных возможностей — возможностей того, что испытуемый ответит верно (неправильно) при условии, что был предъявлен этот стимул. Такие возможности обозначаются так: P (Да/S), P (Да/N), P (Нет/S), P (Нет/N). В частности, первая из этих возможностей имеется возможность верного ответа при условии, что было предъявлено . Легко видеть, что:
P(Да/S) = P(H)/P(S) = n(H)/ N•P(S), (4)
P(Да/N) = P(FA)/P(N) = n(FA)/ N•P(N). (5)
В случае, если вычислены две эти условные возможности, вычисление двух остальных уже не нужно. Они не несут дополнительной информации, т.к.:
P(Нет/S) + P(Да/S) = 1, (6)
P(Нет/N) + P( Да/N) = 1. (7)
Итак, при данных (выбранных экспериментатором) размерах N и P(S) результаты опыта в большинстве случаев воображают лишь двумя условными возможностями: возможностью попадания — p(H)=P(“Да”/S) и возможностью фальшивой тревоги p(FA)=P(“Да”/N).
Увидим, что при всех вышеприведенных расчетах из общего количества N предъявлений в большинстве случаев исключают пара первых (порядка 40—50), предполагая, что в этих первых пробах испытуемый всегда меняет схему соответствия, “подстраивая” ее к информации, взятой от экспериментатора и на протяжении опыта. В то время, когда схема соответствия устанавливается стабильно, говорят, что ответ задачи вышло на асимптотический уровень. Асимптотический уровень характеризуется тем, что в случае, если все число предъявлений (по окончании исключения первых) произвольно разбито на пара групп и по каждой из них в отдельности вычислено P(H) и P(FA), то все эти пары не будут статистически значимо различаться друг от друга.
Полная черта опыта требует указания еще двух факторов: наличие/отсутствие предварительной информации и наличие/отсутствие обратной связи. Предварительная информация — это формальный показатель, означающий сообщение испытуемому величины P(S). К примеру: “В 80% всех проб будет предъявляться безлюдный стимул” (т.е. P(S) = 0,2) либо — “Сигнальное предъявление будет видеться в 3 раза чаще безлюдного” (P(S)/P(N) = 3, т.е. P(S) = 0,75). Сама инструкция, разъяснение испытуемому формы предъявления, характера сигнала и т.п. — все это не входит в термин “предварительная информация”. Увидим, что предварительная информация, если она вводится, возможно и фальшивой, т.е. испытуемому может сообщаться не та величина P(S), которая имеется в действительности. Эта особая модификация “Да-Нет”-опыта, которая тут рассматриваться не будет. Термин обратная сообщение включает данные об истинности/ложности ответов испытуемого, информируемую ему по окончании каждого предъявления, либо сообщение о частоте верных ответов, даваемое по окончании некоей группы (скажем, через каждые 50) предъявлений. В особых модификациях способа такая обратная сообщение кроме этого не всегда должна быть подлинной. Время от времени, к примеру, применяют таковой вариант, в то время, когда по окончании каждой пробы (предъявления) испытуемому с возможностью P(k) информируют серьёзную данные о правильности либо ложности его ответа, а с возможностью 1 — P(k) его “обманывают” (в этом варианте P(k) — формальная мера правдивости обратной связи).
Цель введения предварительной информации и обратной связи — попытка контроля схемы соответствия между особенностями ощущений и решениями, которую устанавливает испытуемый (правила принятия ответа). Разумеется, но, что в случае, если испытуемый не весьма заинтересован в том, дабы почаще отвечать верно, то таковой контроль может оказаться неэффективным. Помимо этого, испытуемый может, устанавливая правило принятия ответа, руководствоваться малоизвестными экспериментатору субъективными “весами” разных типов неточностей. К примеру, он может стараться минимизировать число пропусков и не весьма заботиться об уменьшении числа фальшивых тревог (т.е. “цена” пропуска выше “цены” фальшивой тревоги). Дабы сделать контроль правила принятия ответа более действенным и дифференцированным, обратная сообщение возможно дополнена совокупностью “штрафов” и “выплат”, соответственно за верные и фальшивые ответы, организованной в финансовой либо какой-либо второй (к примеру, легко игровой) форме. Это возможно записать в форме следующей платежной матрицы:
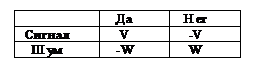 |
где V и W — положительные числа. Такая форма представления особенно эргономична, поскольку она разрешает ограничиться лишь двумя числами, V и W, для чёрта всей платежной матрицы. Матрица именуется симметричной, в случае, если V = W. Для определения оптимального правила принятия ответа, т.е. для того чтобы из имеющегося у наблюдателя комплекта возможностей, которое максимизирует выигрыши, важное значение имеет соотношение не самих V и W, а P(S)·V и P(N)·W (они совпадают, лишь в случае, если P(S) = 0,5). В случае, если P(S)·V = P(N)·W, правило принятия ответа должно быть установлено так, дабы снять возможности неточностей обоих родов. В случае, если же P(S)·V P(N)·W, то правило целесообразно поменять так, дабы сделать допустимо меньшей возможность пропуска, 1-p(H), кроме того в случае, если наряду с этим возрастает возможность фальшивой тревоги, p(FA).
Появляется вопрос: что ограничивает комплект вероятных схем соответствия? По какой причине, например, испытуемый не всегда может выработать “верную” схему соответствия, при которой p(H)=1 и p(FA)=0 ? Ответ на эти вопросы требует построения формальной модели следующих процессов: 1) какое соответствие существует между предъявлениями и и их сенсорными репрезентациями; 2) как по данной сенсорной репрезентации строится ответ (“Да” либо “Нет”). Мы изложим тут одну из несложных моделей, отвечающих на эти вопросы.
Сущность модели пребывает в следующем. Любой стимул ( либо ) связан с его сенсорными репрезентациями стохастически (т.е. вероятностно, случайно), а не детерминистически. Это указывает, что одинаковый стимул, повторяясь в разных пробах, приводит к различным сенсорным образам, так что в каждой отдельной пробе возможно сказать лишь о возможностях происхождения тех либо иных сенсорных образов. Обстоятельства таковой стохастичности бессчётны. С одной стороны, они смогут лежать в природе самого стимула (к примеру, количество квантов, излучаемых источником света в данном направлении в единицу времени — величина принципиально стохастическая) и в ограниченной точности приборных измерений. Иначе, стохастичность связана со случайными флуктуациями в сенсорной совокупности, к примеру, со спонтанной нервной активностью в проводящих дорогах. Последняя, например, снабжает наличие разных сенсорных образов и в том случае, если безлюдный стимул является отсутствием энергии в данной пространственно-временной области. Помимо этого, узнаваемый вклад в стохастичность сенсорных эффектов непременно вносят и без того именуемые внешние факторы: нестабильность стимуляционной аппаратуры, разного рода помехи и т.д.
Потом в излагаемой модели предполагается, что установленное правило соответствия имеет детерминистическую структуру, т.е. этот сенсорный образ, если он в точности повторился в двух пробах (причем за время между пробами схема соответствия не изменилась), позовёт в любой момент одинаковый ответ. Иначе говоря любое правило принятия ответа конкретно разбивает множество всех вероятных ощущений на два класса — один, который связан с ответом “Да”, второй — с ответом “Нет”. На рис. 1 точками заполнены те области, каковые связаны с ответом “Да”. На рис. 2 области с горизонтальной (вертикальной) штриховкой соответствуют ощущениям, каковые смогут быть позваны стимулами и .
Линии 1, 2 и 3 показывают границы разбиения, соответствующего трем схемам соответствия, причем область “Да” при всех схемах соответствия лежит слева от этих границ. Разглядим сперва схему соответствия 1. Мы видим, что при таковой схеме постоянно будет идентифицироваться верно, т.е. p(FA)=0. Но, время от времени (в то время, когда чувство, вызванное , попадает правее
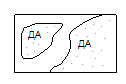 |
Рис.1. Два множества ощущений, вызывающих ответ Да
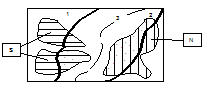 |
Рис.2. Множества непересекающихся ощущений, вызыванных значащим и безлюдным стимулами: S — значащий стимул; N — безлюдный стимул; 1,2 и 3 — линии, показывающие границы разбиения множества ощущений
границы — эта область помечена точками) приведёт к ответу “Нет”, т.е. испытуемый будет время от времени пропускать сигнал, p(H)0. Легко видеть, но, что при данном сорасположении ощущений, вызываемых и , испытуемый может в принципе выработать такую схему соответствия (граница 3, штриховая линия), при которой возможно избежать неточностей, т.е. p(FA)=0 и p(H)=1. Обстоятельство, снабжающая эту возможность, содержится в том, что указанные области не пересекаются, т.е. нет ни одного ощущения, которое имело возможность бы быть позвано (пускай с различной возможностью) как , так и . В случае, если это условие не выполняется (см. рис. 3), то, разумеется, при любой схеме соответствия испытуемый будет выполнять неточности того либо иного рода (O либо FA), или и те, и другие.
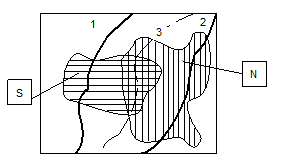 |
Рис. 3. Два пересекающихся множества ощущений, вызванных значащим и безлюдным стимулами
Такова сущность модели. Дабы представить модель в количественной форме, допускаются два дополнительных упрощения. Первое из них возможно разъяснено следующим образом. Схема соответствия с содержательной точки зрения является соответствием данного ответа некоему комплексу особенностей сенсорного образа: “В случае, если образ владеет особенностями таким-то и таким-то, то направляться выбрать ответ “Да”, в другом случае — “Нет”. Разумеется, что не все свойства образа наряду с этим употребляются. Разглядываемое упрощение пребывает в предположении, что ответ принимается в любой момент на базе интенсивности какого-либо одного качества сенсорных образов (“сладкость”, “наклонность”, “яркость” и т.п.), причем правило принятия ответа имеет форму: “В случае, если интенсивность (выраженность) качества больше некоей величины C, то направляться выбрать “Да”, в другом случае — “Нет”. Интенсивность качества, как это видно из прошлой фразы, предполагается представимой настоящим числом. Так все вероятные значения интенсивности данного качества занимают какую-то часть оси настоящих чисел (к примеру, всю хорошую полуось), причем каждое из этих значений при предъявлении данного стимула возможно позвано с тем либо иным правдоподобием. В случае, если значения интенсивности сенсорных образов образуют постоянный континуум, то это правдоподобие выражается не возможностью, а плотностью возможности. Плотность возможности происхождения ощущения со значением интенсивности ощущения X при подаче стимула A условимся обозначать через f (X/A).
Возвратимся сейчас к нашей ситуации, где стимул имеется или , или . Каждому из стимулов соответствует собственная функция плотности возможности: f (X/S) и f (X/N) (рис. 4).
В соответствии с принятому утверждению, правило принятия ответа определяется выбором граничной точки C (ее еще именуют критической точкой либо величиной критерия принятия ответа о наличии сигнала), таковой, что в случае, если интенсивность X в данной пробе превышает C, то направляться ответ “Да”, в случае, если же не превышает, то — “Нет”. Легко видеть по рисунку, что возможность фальшивой тревоги p(FA) равна возможности того, что интенсивность X (при условии, что предъявлен ) превзойдет C, т.е. равна заштрихованной области под кривой f (X/N). Возможность попадания p(H) равна возможности того, что X (при условии, что предъявлен ) превзойдет C, т.е. равна незаштрихованной области под кривой f (X/S).
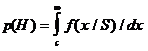 |
(8)
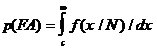 (9)
(9)
В случае, если критерий C находится на большом растоянии вправо (продемонстрировано на рис. 4 одной стрелкой), то, разумеется, p(FA)=p(H)=0. В случае, если сейчас начать двигать критерий справа налево, то при каждом очередном значении мы будем приобретать новую несколько p(FA) и p(H), причем оба значения будут возрастать (либо по крайней мере не убывать), до тех пор пока при достаточно далеком левом положении C оба не станут равны 1 (продемонстрировано двумя стрелками на рис. 4). Потому, что каждое значение C конкретно определяет несколько чисел p(FA) и p(H), то ему возможно поставить в соответствие точку в квадрата (рис. 5), на вертикальной стороне которого откладывается p(H), а на горизонтальной — p(FA), и так представить итог работы наблюдателя .
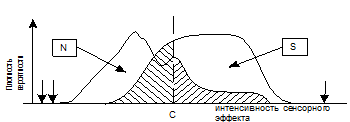 |
Рис. 4. Неспециализированная модель обнаружения сигнала: справа – распределение сенсорных эффектов при действии значащего стимула, слева – безлюдного стимула
Полученная по этим точкам кривая именуется рабочей чёртом наблюдателя либо легко — PX. Каждая пара распределений, f(X/S) и f(X/N) конкретно определяет PX, но обратное неверно: одинаковая PX может определяться разными парами f(X/S) и f(X/N). PX идет из точки (0,0) квадрата в точку (1,1) и наряду с этим находится выше его основной диагонали. Последнее направляться из того, что распределение f(X/S) перемещено вправо довольно f(X/N), т.е. p(H) превышает p(FA).
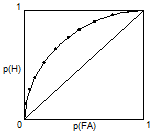 |
Рис.5. Рабочая черта совершенного наблюдателя
Возможности p(H) и p(направляться) изменяются содружественно, т.е. запрещено лишь методом трансформации схемы соответствия в один момент расширить одну из них и уменьшить другую (либо, что то же самое, запрещено в один момент уменьшить либо расширить возможности неточностей обоих родов, FA и O). Это крайне важное положение правильно для любых пар f(X/S) и f(X/N). Из него направляться, что лишь пара этих возможностей, а не каждая в отдельности, характеризует сенсорную свойство наблюдателя.
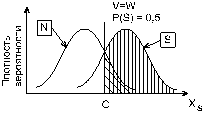
Допустим, в опыте с симметричной платежной матрицей (V=W) и P(S) = 0,5) испытуемый установил положение критерия, как это продемонстрировано на рис. 6а.
 |
||||
 |
||||
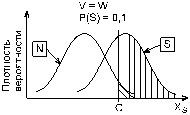 |
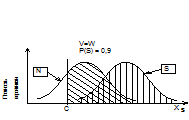
Рис.6. Модели обнаружения сигнала:
а — симметричный; б -либеральный; в -твёрдый критерий принятия ответа; вертикальная штриховка — p(H), косая — p(FA)
Результаты этого мысленного опыта с так называемым симметричным критерием представлены в таблице 3.
Это положение критерия оптимально в том смысле, что суммарный выигрыш испытуемого в этом случае будет велик.
Пускай сейчас в следующем опыте платежная матрица осталась симметричной, а P(S)=0.9.
Таблица 2
Возможности финалов опыта с симметричной платежной матрицей и P(S)=0.5
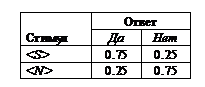 |
Таблица 3
Возможности финалов опыта с симметричной платежной матрицей и P(S)=0.9
Таблица 4
Возможности финалов опыта с симметричной платежной матрицей и P(S)=0.1
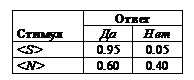 |
Сейчас (рис. 6б), дабы сохранить тот же выигрыш, наблюдателю нужно переместить критерий так, дабы p(H) быстро возросло, кроме того за счет возрастания p(FA) — сейчас серьёзнее не пропустить сигнал, чем не дать фальшивую тревогу! Следовательно, критерий C сдвинется влево. В этом случае говорят, что наблюдатель применяет либеральный критерий.
Пускай в третьем опыте при симметричной платежной матрице P(S) установили равной 0.1.
В данной ситуации (рис. 6в) критерий должен быть сдвинут вправо, и в этом случае говорят об применении строгого критерия. Подобные трансформации положения критерия принятия ответа возможно разглядеть и при трансформациях платежной матрицы при постоянной величине P(S).
Для каждой пары f(X/S) и f(X/N), в случае, если заданы V,W и P(S), возможно вычислено оптимальное положение C — то, при котором выигрыш велик. В cоответствии с данной логикой возможно изучить вопрос, как настоящее положение критерия, выбираемое испытуемым, близко к оптимальному. Но, очевидно, это возможно сделать только в том случае, если мы можем вернуть по экспериментальным результатам теоретическую схему, т.е. выстроить функции распределения f(X/S) и f(X/N) и отыскать критерий C.
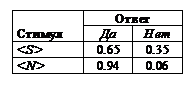 |
Итак, перед нами стоит задача восстановления теоретической схемы по экспериментальным данным. В первую очередь, разберемся в том, что являются экспериментальные эти. Пускай выбраны стимулы и и совершён опыт по способу “Да-Нет”. Результатом опыта есть пара возможностей p(H), p(FA). Потом какие-то параметры опыта изменяются (изменятеся P(S) и/либо платежная матрица, либо снимается обратная сообщение и заменяется на предварительную данные либо что-то еще), и опыт повторяется с теми же и . Приобретаем, по большому счету говоря, другую несколько p(H), p(FA). Повторяя опыт пара раз, мы будем иметь в следствии пара пар p(H), p(FA), т.е. пара точек PX. Очевидно, и это крайне важно, мы можем вычислять все эти пары p(H) и p(FA) точками одной PX только постольку, потому, что предполагается, что трансформации экспериментальных параметров смогут привести лишь к трансформации положения критерия C, но не к трансформации схемы соответствия, в более широком смысле слова включающем вероятное привлечение новых сенсорных качеств, замену одного качества на второе и в следствии, в случае, если это новое уровень качества одномерно, — получению новой пары распределений f(X/S) и f(X/N). Так, неприятность формулируется так: по нескольким точкам PX необходимо вернуть f(X/S), f(X/N) и C. Но, мы уже говорили, что в таком виде неприятность не решается, поскольку кроме того если бы была известна вся PX (т.е. все точки, а не пара, чего ни при каких обстоятельствах, конечно, не бывает), распределения f(X/S) и f(X/N) не восстановимы конкретно. Исходя из этого в модели, которую мы излагаем (в большинстве случаев именуемой, не смотря на то, что и не совсем совершенно верно, теорией обнаружения сигналов, ТОС) принимается еще одно упрощающее предположение (но, в отличие от первого, оно допускает прямую экспериментальную диагностику, о чем обращение отправится ниже): существует такая монотонная изменение оси интенсивности, из-за которой оба распределения становятся обычными. Для краткости трансформированную ось мы будем обозначать легко через z и сказать о z-значениях. Под монотонной изменением понимается совокупность всевозможных сжатий и растяжений разных областей оси X так, что в случае, если точка q лежит левее r, то по окончании трансформации это отношение сохраняется. Примером таковой трансформации есть логарифмирование, растягивающее хорошую полуось настоящих чисел на всю настоящую ось. Итак, мы имеем два обычных распределения, причем в любой момент можно считать, что на оси выбрана такая такой масштаб и позиция нуля, что f(Z/N) имеет центр в стандартное отклонение и нуль, равное 1. Для восстановления теоретической картины, так, нужно выяснить стандартное отклонение и положение центра распределения f(Z/S).
В случае, если допустить, что ss,n= 1, т.е. дисперсии обоих распределений равны, а центр распределения f(Z/S) сдвинут вправо от центра распределения f(Z/N) на величину a, тогда
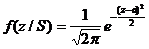 |
(10)
В этом случае вместо a обыкновенно пишут особый знак d’ и именуют эту величину мерой чувствительности наблюдателя к сигналу. Чувствительность к сигналу характеризуется степенью отличия Z-размеров, вызываемых , от Z-размеров, вызываемых . Чем меньше величина d’, тем больше перекрываются области Z-значений, соответствующих и (рис. 7).
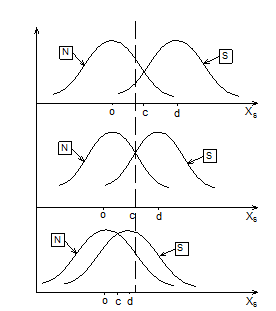 |
Рис. 7. Модель ТОС при разных уровнях обнаружимости сигнала
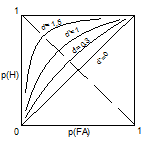
Легко видеть, что при одном и том же положении критерия C, а следовательно, при одной и той же величине p(FA), величина p(H) тем ближе к p(FA), чем меньше d’. В случае, если d’ = 0, то p(FA) = p(H) при всех C и, следовательно, PX в таком опыте сходится с основной диагональю квадрата (рис. 8). В случае, если d’ 0, PX лежит выше диагонали и имеет ровный и симметричный вид довольно побочной диагонали, идущей из (0,1) в (1,0). Чем больше d’, тем более выпукла PX влево-вверх и тем дальше она отстоит от основной диагонали. Как же фактически вычислить d’ и C по итогам опыта? какое количество точек PX направляться для этого иметь?
Оказывается, достаточно лишь одной точки, т.е. лишь одной пары p(FA), p(H). Вправду,
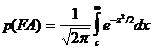 |
(11)
Это уравнение нужно решить довольно C. Введем новый термин: нахождение C по P в уравнении (12):
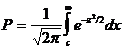 |
(12)
именуется Z-преобразованием P:
C = Z [P]. (13)
 |