где si и sj — дисперсии процессов различения i-го и j-го стимулов, соответственно, а ri,j— имеется корреляция между мгновенными значениями процессов различения стимулов i и j.
Разглядим сейчас следующую обстановку. Пускай наблюдателю предъявляются пары стимулов i и j и от него требуется осуществить суждение, какой из стимулов дальше отстоит от нуля на психотерапевтическом континууме (к примеру, более тяжелый либо более сложный, либо более прекрасный и т.д.). На рис. 1 продемонстрированы гипотетические процессы различения стимулов i и j.
Предполагается, что в случае, если различительный процесс для стимула j окажется на психотерапевтическом континууме выше, чем для стимула i, т.е. в случае, если различительная разность (dj — di) 0, то последует суждение, что стимул j больше, чем стимул i. И соответственно при (dj — di) 0 — случится обратное суждение.
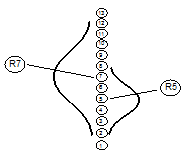 |
Рис.1. Гипотетическая модель процесса различения 2-х стимулов
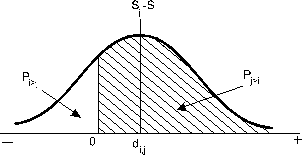 |
Рис. 2. Гипотетическое распределение процессов различения стимулов Sj и Si на психотерапевтическом континууме: заштрихованная область показывает частоту суждения: стимул j больше, а незаштрихованная — стимул j меньше; dij — различие шкальных значений стимулов i и j, измеренное в единицах стандартного отклонения данного распределения — s (dj-di)
Но, в случае, если распределения различительных процессов перекрываются, то суждение, что стимул j меньше, чем стимул i может случиться кроме того тогда, в то время, когда величина Sjна психотерапевтическом континууме больше, чем величина Si. На рис. 2 продемонстрировано распределение различительных разностей при солидном числе суждений.
Среднее распределения равняется различию шкальных размеров двух стимулов — (Sj — Si). Это различие возможно отыскать из таблицы областей под единичной обычной кривой, зная пропорцию суждений стимул j больше, чем стимул i от общего числа суждений по данной паре стимулов (т.е., сделав стандартное преобразование “p ® z” ).
В единицах дисперсии s(dj- di) это возможно записать так:
Sj — Si= zj,is(dj- di ), (2)
где zj,i— обозначает искомое различие.
Подставляя это выражение в уравнение (1), возьмём:
Sj — Si = zj,i(sj2+ si2-2ri,jsisj )1/2 . (3)
Уравнение (3) и высказывает в общем виде закон сравнительных оценок Терcтоуна.
§ 2. Процедура измерения
Эмпирическим материалом, на котором основан закон Терcтоуна, помогают суждения по типу: “стимул i более … тяжелый, увлекательный, прекрасный и т.д., чем стимул j”. Прямой способ для получения таких оценок именуется способом парных сравнений. В принципе это тот же самый способ константных стимулов, лишь в этом случае в качестве эталона выступает поочередно любой стимул. Испытуемый осуществляет попарное сравнение всех стимулов. Каждое сравнение производится неоднократно. На основании этих сравнений для каждой пары определяется частота предпочтения одного стимула второму. Квадратная матрица (n x n) этих частот (обозначим ее буквой F) воображает данные. Диагональные элементы данной матрицы будут безлюдными, потому, что аналогичные пары в большинстве случаев не предъявляются. Разумеется, что сумма элементов fi,jи fj,iв сумме будет равна неспециализированному числу сравнений.
Последующий анализ содержится в переходе от матрицы частот (F) к матрице возможностей (обозначим ее буквой P). Элемент данной матрицы pi,jесть пропорция числа предпочтений i-го стимула j-му в общем числе сравнений этих двух стимулов. Диагональ матрицы P кроме этого не заполнена, а сумма симметричных элементов довольно данной диагонали равна единице (т.е. pi,j+ pj,i= 1). Из матрицы возможностей уже легко выяснить матрицу различий Z, памятуя о том, что различие выражается в единицах обычного отклонения. Значение zi,jдля соответствующей возможности возможно выяснить по таблице областей под единичной обычной кривой. Для всех pi,j0,5 величина z будет хороша, а для всех pi,j
Разглядим сейчас, как соотносятся данные с теоретической формой их выражения. Число свободных элементов в матрице F равняется n(n-1)/2, где n — число стимулов. В то время как закон сравнительных оценок, выраженный в формуле (3), имеет для тех же n стимулов и n малоизвестных шкальных значений, n малоизвестных дисперсий различительных процессов и n(n-1)/2 малоизвестных корреляций. Очевидно, что при таком соотношении числа уравнений — n(n-1)/2 и числа малоизвестных — 2n+n(n-1)/2, решить данную совокупность нереально. Исходя из этого нужно ввести условия, упрощающие структуру выражения (3).
§ 3. Упрощенные варианты закона сравнительных суждений
Терcтоун разглядывал 5 вариантов применения этого закона. Первый вариант — это та исходная неспециализированная форма закона, о которой уже говорилось. Второй вариант разглядывает изменение экспериментальной методики, обращаясь от оценок, создаваемых одним испытуемым, к групповым оценкам. Любой испытуемый в этом случае создаёт лишь одно сравнение. И лишь третий, четвертый и пятый варианты вводят дополнительные допущения, каковые меняют неспециализированную форму выражения (3).
Торгерсон (1958) внес предложение развести эти варианты на два класса. К первому классу относятся трансформации в методике проведения опыта. Это первый и второй варианты Терcтоуна, и помимо этого, Торгерсон внес предложение отнести ко мне и смешанный опыт, в то время, когда пара испытуемых сравнивают по паре пар и все оценки сводятся в неспециализированную матрицу частот. Ко второму классу относятся трансформации в форме закона сравнительных оценок. Ко мне относятся 3, 4 и 5 варианты Терcтоуна либо, соответственно, условия А, В и С, каковые внес предложение Торгерсон.
III вариант Терcтоуна. Предполагается, что корреляция между различительными процессами ri,jв выражении (3) равна нулю. При таких условиях закон сравнительных оценок принимает форму:
Sj — Si= zj,i(s2j + si2 )1/2 . (4)
Торгерсон предлагает тут менее твёрдое ограничение, с условием (условие А), что ковариация в выражении (3) — равна постоянной величине (d). Тогда :
Sj — Si = zj,i(sj2+ si2 — d)1/2. (5)
Но фактически выражения (4) и (5) аналогичны, потому, что ковариация есть постоянной лишь тогда, в то время, когда корреляция пытается к нулю.
IV вариант Терстоуна основывается на допущении, что ri,j=0 и что дисперсии различения слабо отличается друг от друга, т.е. si= sj+ d, где d мало если сравнивать с sj. Тогда выражение (3) преобразуется в
Sj — Si = zj,i[sj2+ (sj+ d2)]1/2. (6)
Раскрывая скобки и делая последовательность упрощений и преобразований, приобретаем окончательную форму четвертого варианта закона:
Sj — Si = zj,iс(sj + si ), (7)
где с — постоянный множитель.
Более не сильный допущение Торгерсона (условие В) о константности корреляции ведет к выражению:
Sj — Si = zj,i[1/2(1 — r)1/2(sj + si )]. (8)
Выражения (7) и (8) отличаются лишь постоянными участниками, исходя из этого вариант Торгерсона имеет определенные преимущества.
V вариант закона сравнительных оценок Терстоуна отыскал громаднейшее использование благодаря простоты собственной формы. Данный вариант основывается на допущении нулевой корреляции между двумя процессами различения (r = 0) и равенства различительных дисперсий этих процессов (sj = si= s). Тогда выражение (4) преобразуется в:
Sj — Si = zj,is . (9)
Обозначив константный член уравнения буквой “c”, возьмём:
Sj — Si = сzj,i. (10)
Уравнение (10) сходится по собственной неспециализированной форме с разными модификациями данного варианта, каковые предлагали потом кое-какие авторы. самая интересная модификация предложена Мостеллером (1951) и пребывает в константной равенства корреляции и допущении дисперсий. В этом случае величина “с” в уравнении (10) будет равна [2(1 — r)]1/2, а уравнение получает следующий вид:
Sj — Si = zj,i[2(1 — r)]1/2. (11)
Сравнивая упрощенные варианты (4), (7), (10) с исходной формулой (3), легко видеть, что кроме того самый сложный из упрощенных вариантов (4) уже имеет, по крайней мере теоретически, ответ, в то время, когда число стимулов (n) равняется 5. Остальные варианты еще легче. Но практическая процедура в любой момент более трудоемка и менее красива, чем это обещает теоретическая модель. Обстоятельство этого по большей части лежит в эмпирической природе исходных оценок, в их зашумленности множеством случайных факторов, от которых нереально оградить испытуемого. Для устранения случайных неточностей предлагается следующая тактика. Число стимулов расширить так, дабы совокупность уравнений была существенно переопределена. К примеру, для варианта III брать не 5 стимулов, а 10 – 15. Для решения применять итеративную вычислительную процедуру, которая учитывает тот факт, что случайные неточности имеют тенденцию взаимоуравновешиваться.
Такие процедуры были созданы различными авторами, и в данной работе будет обрисован метод Мостеллера (1951) для V варианта закона в модификации Торгерсона (1958). Метод применяет ответ способом мельчайших квадратов. Он дает возможность приобрести более правильные оценки шкальных значений из матрицы в случае, если она не имеет безлюдных элементов.
§ 4. Процедура ответа V варианта закона сравнительных оценок для полной матрицы
В V варианте закона, записанном в общем виде (9), единицы измерения шкальных значений в любой момент возможно подобрать так, дабы константа “с” была равна 1. Тогда:
Sj — Si = zj,i. (12)
При отсутствия неточностей в оценках искомое различие будет равняется замечаемому (обозначим его z’j,i). Но в следствии неточностей между z’j,iи zj,iбудет некое расхождение a. Задача содержится в получении для того чтобы множества оценок шкальных значений стимулов, для которых сумма квадратов всех расхождений есть минимальной, т.е. нужно минимизировать величину
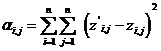 (13)
(13)
Подставив вместо zi,jшкальные значения, возьмём:
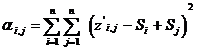 |
(14)
Все ai,jдля всех zi,jиз матрицы Z дадут матрицу неточностей a. Дабы минимизировать каждую ai,j, нужно забрать личную производную ai,jпо Siи Sj. Каждое частное значение Siв матрице неточностей a появляется лишь в i-той строке и i-том столбце, но потому, что матрица неточностей так же кососимметрична [zi,j= -zj,iи (Si-Sj)= -(Sj-Si)], как и матрица Z, то для каждой Siчастная производная будет касаться лишь i-го столбца. Дифференцируя элементы каждого столбца по Si, возьмём:
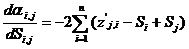 |
(15)
где i = 1,2 … , n.
Приравняем личную производную нулю и по окончании переноса возьмём:
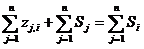 (16)
(16)
Поделим выражение (16) на n и заберём начальное значение шкалы, равное . В следствии возьмём:
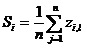 (17)
(17)
где i=1,2 … , n
Так, для минимизации неточности нужно среднее арифметическое по столбцу матрицы Z и мы возьмём оптимальное значение шкальной величины Si.
Разглядим практический пример ответа V варианта закона сравнительных оценок способом мельчайших квадратов (эти вымышлены). Испытуемому в случайном порядке предъявляются 6 цветных карт из малого комплекта теста Люшера и просят в каждой паре выбрать самый красивый. Любая пара предъявляется по 50 раз. В итоге для одного из испытуемых была взята следующая матрица частот F (табл.1):
Таблица 1
Матрица частот F
 |
Примечание. Элементом матрицы fi,jявляется частота, с которой в паре j,i стимул i оценивался более прекрасным, чем стимул j.
Полученная матрица частот F преобразуется в матрицу возможностей P делением частоты fi,jна число предъявлений (N=50).
Таблица 2
 Матрица возможностей P
Матрица возможностей P
Примечание. Элементом матрицы pi,jявляется возможность, с которой стимул i в паре j,i оценивался более прекрасным, чем стимул j.
Каждое значение возможности pi,jиз матрицы P переводится потом посредством таблицы в единицы стандартного отклонения обычной кривой — zi,j, по которым и вычисляются шкальные значения Siкаждого стимула.
Таблица 3
Матрица Z ? оценок
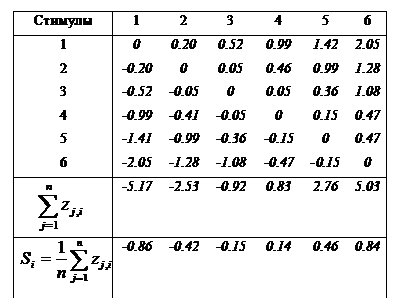 |
Примечание. Элементом матрицы zi,jявляется возможность pj,i, преобразованная в единицы стандартного отклонения.
Рассмотренная процедура позволяет для каждого стимула Siполучить его значение на шкале промежутков.
§ 5. Процедура ответа V варианта закона сравнительных суждений для неполной матрицы данных
Настоящие экспериментальные эти часто отличаются от той хорошей матрицы данных, которая анализировалась выше. Самый распространенный артефакт в процедуре парного сравнения, что связан с ограничением на вероятное число предъявлений, — стопроцентное предпочтение одного стимула второму, что ведет к появлению в матрице единиц и вероятностей нулей. единица и Ноль в терминах модели Терcтоуна не несут сравнительной информации о различии стимулов, исходя из этого не смогут быть использованы для расчетов шкальных значений стимулов.
Для матриц с единицами и нулями (они именуются неполными матрицами) существуют особенные методы анализа. Самый распространенный из них детально обрисован в работе Торгерсона (1958) и кратко пребывает в следующем.
Из выражения (12) для стимула j направляться, что стимул j+l будет описываться следующим выражением:
Sj+e — Si = zj,i+e . (18)
Вычтя из уравнения (18) уравнение (12), мы возьмём сравнительное различие для интересующего нас стимула косвенным методом. В терминах минимизированной неточности эта величина возможно вычислена из выражения:
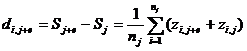 (19)
(19)
где nj— имеется индекс суммирования.
Для практического удобства матрицу Z направляться перестроить так, дабы столбцы были упорядочены по величине. Порядок столбцов в матрице Z определяется суммой по столбцу матрицы P. Для таковой упорядоченной матрицы Z различие Sj+e — Siможно прямо вычислить из выражения (19). В случае, если мы шкальное значение первого стимула (Si) приравняем к нулю, то шкальное значение любого стимула имеется сумма расстояния и шкального значения стимула между данным стимулом и предшествующим:
S1= 0,
S2= d1,2 ,
S3 = S2+ d2,3 ,
Sn= Sn-1+dn-1,n . (20)
Разглядим практический пример ответа для неполной матрицы частот, забранный из работы Торгерсона (1958). Пускай нам дана матрица возможностей предпочтения i-го стимула j-му с некоторыми вырожденными (безлюдными) элементами, равными 0 либо 1.
Таблица 4
Матрица возможностей P
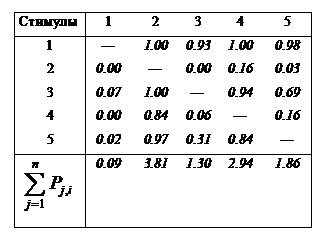 |
Примечание. Элементом матрицы pi,jявляется возможность, с которой стимул i в паре j,i оценивался более предпочтительным, чем стимул j.
Преобразуем возможности pi,jв единицы стандартного отклонения обычного распределения — zi,j.
Таблица 5
Матрица Z — оценок
 |
Примечание. Элементом матрицы Zi,jявляется возможность pj,i, преобразованная в единицы стандартного отклонения.
Таблица 6
Матрица Z’ — оценок
 |
Примечание. Элементом матрицы Z ’i,jявляется возможность p’j,i, преобразованная в единицы стандартного отклонения. . Столбцы упорядочены по возрастанию
Переставим столбцы в матрице Z в таком порядке, дабы первый столбец имел мельчайшую сумму элементов, а последний — громаднейшую.
Из матрицы Z’ возможно взять матрицу различий между соседними парами столбцов, вычитая их поэлементно один из другого. В каждой j-й строке элемент данной матрицы будет равен ( zj,i+1- zj,i).
Пользуясь выражением (20), вычисляем из взятых различий шкальные значения стимулов, приняв, что S1= 0:
S1= 0,
S3 = 0 + 1.5 = 1.5,
S5= 1.5 + 0.53 = 2.03,
S4= 2.03 + 0.98 = 3.01,
S2= 3.01 + 0.56 = 3.97.
Из рассмотренной процедуры видно, что недостающие элементы матрицы компенсируются наличием внутренней связи между элементами столбца, что разрешает разглядывать разность между столбцами матрицы как следствие алгебраической интерполяции отсутствующих элементов в столбце.
Таблица 7
Матрица разностей между столбцами
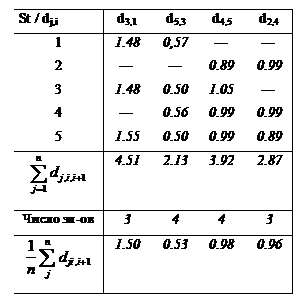 |
Литература
1. Терстуон Л.Л. методы психофизики // и Психофизический анализ Проблемы / Под ред. А.Г.Асмолова, М.Б.Михалевской. М.: Изд-во Моск. ун-та, 1974.
2. Guilford J. P. Psychometric Methods. N. Y., Toronto, London: Mc-Grow-Hill, 1954.
3. Torgerson N.S. Theory and Method of scaling. N. Y.: John Wiley and Sons, 1958.
Методические указания по исполнению учебного задания по теме “Способ парных сравнений”
Задание 1. Построение шкалы цветовых предпочтений способом парных сравнений
Цель задания: Освоить способ парных сравнений для построения шкалы промежутков. Сравнить выстроенную шкалу со шкалой порядка, взятую способом балльной оценки.
Методика
Аппаратура. Задание выполняется на IBM-совместимом персональном компьютере. Для предъявления сигнала “Внимание” употребляются головные телефоны, соединенные со звуковым синтезатором ПК. Для исполнения учебного задания употребляется компьютерная программа parcom.exe и mbe.exe1.
Стимуляция. На экране монитора предъявляются цветные прямоугольники из комплекта восьмицветного теста цветовых предпочтений Люшера: светло синий, зеленый, красный, желтый, фиолетовый, коричневый, тёмный и серый.
Процедура опыта. При отработке задания любой студент выступает сперва в роли испытуемого, а после этого обрабатывает личные эти. Испытуемый сидит на расстоянии 1 м от экрана дисплея. Опыт складывается из 2-х серий.
В первой серии испытуемому предлагается оценить по 10-балльной шкале приятность каждого цвета. Для этого на экране монитора ему предъявляется вертикальная графическая шкала с десятью оценочными градациями от “невообразимо приятный — 10 баллов” до “невообразимо неприятный — 0 баллов” . Внизу экрана в случайном порядке расположены 8 цветных прямоугольников. Применяя клавиши управления перемещением курсора и , испытуемый может перемещать белую рамку от одного прямоугольника к второму и, так, осуществлять собственный выбор. Выбрав тот стимул, что необходимо оценить, испытуемый нажимает на клавишу “Tab” и вводит необходимое число от 0 до 10. Cправа от графической шкалы на соответствующем месте появляется прямоугольник того же цвета, а в нижнем последовательности он исчезает. Действуя так, испытуемый поочередно оценивает все 8 стимулов.
Во второй серии цветные прямоугольники предъявляются парами, и задача испытуемого содержится в том, дабы оценить, какой из 2-х цветов ему нравится больше. Для ответа употребляются две клавиши управления перемещением курсора: (левый нравится больше) и (правый нравится больше). Когда испытуемый дает ответ, на экране появляется следующая пара стимулов. Всего предъявляются 144 пробы, т.е. все цвета видится между собой по 6 раз. Три раза любой из цветов предъявляется слева, три раза — справа. В верхнем правом углу экрана любой раз высвечивается порядковый номер пробы.
Обработка результатов. По окончании опыта студенту выдается компьютерная распечатка, в которой представлены: 1) по итогам первой серии — балльные оценки всех 8 цветов; 2) по итогам второй серии — усредненная по 6 предъявлениям матрица частот (F) — 8×8, элементом матрицы fi,jявляется частота, с которой в паре j,i стимул i оценивался более прекрасным, чем стимул j. При необходимости возможно переписать на дискету файл с данными: его имя соответствует фамилии испытуемого, написанной латинскими буквами, а расширение — mpc.
Обработка результатов содержится в построении по каждой серии личной и групповой шкал1. Согласно данным, взятым в первой серии, строится шкала порядка, согласно данным второй серии — шкала промежутков. Для получения групповых данных любой испытуемый обязан свести в таблицу и усреднить собственные эти с данными вторых четырех испытуемых. Причем в отвлечённой группе студентов (в большинстве случаев, 12 — 15 человек) не должно быть повторяющихся результатов.
Обсуждение результатов. При дискуссии взятых результатов любой испытуемый обязан сравнить размещение стимулов по шкале интервалов и шкале порядка и сделать заключение о недостатках и преимуществах каждого способа. Стоит поразмыслить о метрических преимуществах шкалы промежутков, и об отражении в шкальных значениях более узких изюминок сходства либо различия между стимулами. Помимо этого, нужно дать сравнительную оценку личной и групповой шкал.
направляться кроме этого сопоставить исходные положения модели с взятыми в опыте результатами и сделать выводы (относительно с другими способами) о недостатках и преимуществах способа парных сравнений.
Глава 3. СПОСОБЫ ПРЯМОЙ ОЦЕНКИ
В соответствии с самый распространенной мнению группу способов, каковые разрешают взять количественную оценку психотерапевтической величины на шкале промежутков либо взаимоотношений как яркий итог измерительной процедуры, именуют способами прямого шкалирования. Прямое шкалирование базируется на предположении о наличии у человека внутренней шкалы измеряемого психотерапевтического показателя, имеющей единицу измерения и начальную точку, и, следовательно, способности выносить количественные суждения довольно собственных ощущений. Другие, рассмотренные выше способы одномерного шкалирования (способы балльных парных и оценок сравнений), являются прямыми лишь для порядковой шкалы. Шкалы более большого порядка смогут быть выстроены при применении этих способов лишь при введения дополнительных теоретических допущений, к примеру, допущение о обычном характере распределения измеряемого показателя позволяет взять вместо порядкового измерение на шкале промежутков.
Второй суть заглавия прямого шкалирования пребывает в том, что им подчеркивается простота, самый короткий путь от измерительной процедуры, в которой исследователь приобретает “сырые” эти, до построения субъективной шкалы, потому, что шкальное значение измеряемого психотерапевтического показателя выражено в содержании ответа испытуемого. Конструирование шкал промежутков либо взаимоотношений посредством непрямых способов (косвенное шкалирование) требует кроме дополнительных теоретических допущений еще и последовательности статистических манипуляций, т.е. осуществляется более опосредованным и трудоемким методом.
Во всех способах прямого шкалирования употребляются два типа организации ответных реакций испытуемого на протяжении измерения: процедура оценки, в то время, когда от испытуемого требуется лишь информировать собственные суждения о предъявляемых ему объектах, и процедура воспроизведения, благодаря которой экспериментатор определит о субъективных оценках испытуемого по тому, как он воспроизводит заданные размеры, промежутки либо ощущения, регулируя величину измеряемого параметра объекта.
К числу прямых способов, приводящих к интервальной шкале, относится способ кажущихся равными промежутков (второе его наименование – способ категориальной оценки), способ последовательных промежутков и способ равных сенсорных расстояний (в противном случае он именуется способом воспроизведения категорий).
Шкала взаимоотношений возможно взята из результатов измерения при применении способа оценки взаимоотношений, способа постоянных сумм, способа установления заданного отношения (мультипликация и фракционирование), метода оценки воспроизведения и метода величины заданной величины.
Заслуга введения этих способов в широкую практику психотерапевтических измерений в собственности С.С. Стивенсу. Ниже будут детально рассмотрены два способа из вышеперечисленных – способ установления заданного отношения и способ оценки величины.
§ 1. Способ установления заданного отношения
1. Модификации способа установления заданного отношения.
Известны две модификации способа установления заданного отношения: способ фракционирования (деления) и способ мультипликации (умножения). В способе фракционирования (деления) испытуемому предъявляют поочередно пара стандартных стимулов (Sst) и просят подобрать к каждому из них среди предъявляемых ему на сравнение стимулов (Sc) такие, величины которых составляют заданную часть от соответствующих Sst. В большинстве случаев задаются простые дроби типа 1/n = 1/2, 1/3 и т.п. Значительно чаще употребляется 1/n = 1/2, т.е. “деление пополам”. При подборе стимула, находящегося в заданном отношении к Sst, употребляются процедуры оценки либо воспроизведения.
Способ мультипликации (умножения) отличается от фракционирования лишь тем, что испытуемый обязан подбирать к стандартному стимулу таковой, что превышает его в заданное число раз, т.е. n1.
2. Требования к шкалируемому показателю.
мультипликации и Методы фракционирования смогут использоваться для шкалирования лишь в том случае, в то время, когда шкалируемый показатель удовлетворяет двум условиям:
1. Испытуемый должен иметь возможность замечать изменение переменного стимула, благодаря которому он подбирает заданное отношение, как постоянное либо с малый шагом. В другом случае он не сможет совершенно верно установить заданное отношение.
2. Субъективному шкалируемому показателю обязана соответствовать физическая шкала стимулов, потому, что построение субъективной шкалы данным способом допустимо лишь через определение психофизической функции, связывающей величины ощущений со стимульными значениями. Дело в том, что способом установления заданного отношения возможно измерить (т.е. сопоставить со шкальными значениями одной и той же шкалы взаимоотношений) ощущения, вызванные не всеми, а лишь некоторыми стимулами (Sst). К примеру, в случае, если заданное отношение равняется 1/n, то конкретно смогут быть выяснены шкальные значения ощущений, вызванных лишь стимулами, равными na, где a = ± 1,2,3,…,n. В случае, если 1/n = 1/2, то в опыте возможно взять лишь следующие шкальные значения: 1/16, 1/8, 1/4, 1/2, 1, 2, 4, 8, 16 … Но для любого шкального значения, лежащего между соседними, позванными стимулами naи na+1, в общем случае запрещено конкретно указать соответствующий ему стимул. Им возможно любой стимул, лежащий между naи na+1, и выяснить его возможно лишь при наличии психофизической функции.