Чтобы выяснить, как Эверетт пришёл к собственному открытию, направляться иметь чуть большее представление об уравнении Шрёдингера. Я уже подчёркивал, что уравнение не разрешает волнам возможности неожиданно схлопываться. Но по какой причине? И что оно разрешает ? Давайте попытаемся осознать, как уравнение Шрёдингера руководит волной возможности по мере её распространения во времени.
Это совсем несложно, в силу того, что уравнение Шрёдингера относится к одному из самых несложных классов математических уравнений, характеризующихся свойством линейности — математическим олицетворением того, что целое имеется сумма собственных частей. Чтобы выяснить, это что может значить, представим, что график на рис. 8.7а — это некая волна возможности электрона ровно в 12 часов дня (для большей наглядности я буду применять волну возможности, зависящую от положения на прямой, изображённой горизонтальной линией, но это не умаляет общности обсуждаемых идей). Посредством уравнения Шрёдингера возможно смотреть за распространением данной волны вперёд во времени и определить, какова будет её форма, скажем, в час дня (рис. 8.7б . Сейчас отметим следующее. Как продемонстрировано на рис. 8.8а , исходную форму волны возможно разложить на два более несложных кусочка; в случае, если объединить две волны на рисунке, складывая их значения точка за точкой, возможно вернуть исходную форму волны. Линейность уравнения Шрёдингера свидетельствует, что его возможно использовать раздельно для каждого кусочка на рис. 8.8а , определяя вид каждого фрагмента волны в час дня, и после этого, объединяя результаты, в соответствии с рис. 8.8б , возможно будет взять полный ответ, продемонстрированный на рис. 8.7б . В разложении на два фрагмента нет ничего сакрального; исходную волну возможно разложить на любое число составляющих, разглядеть каждую раздельно, после этого объединить полученные результаты для получения окончательной формы волны.
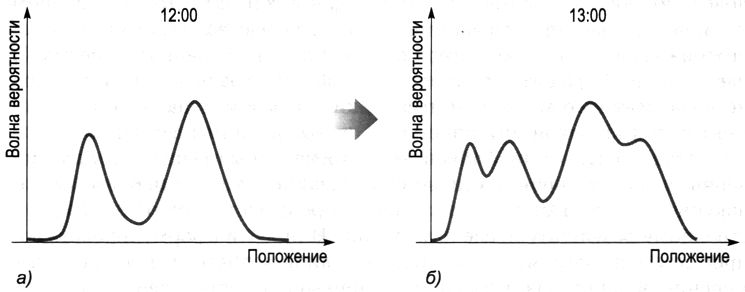
Рис. 8.7. а ) Изначальная форма волны возможности эволюционирует в соответствии с уравнению Шрёдингера, переходя в другую форму (б ) в последующий момент времени
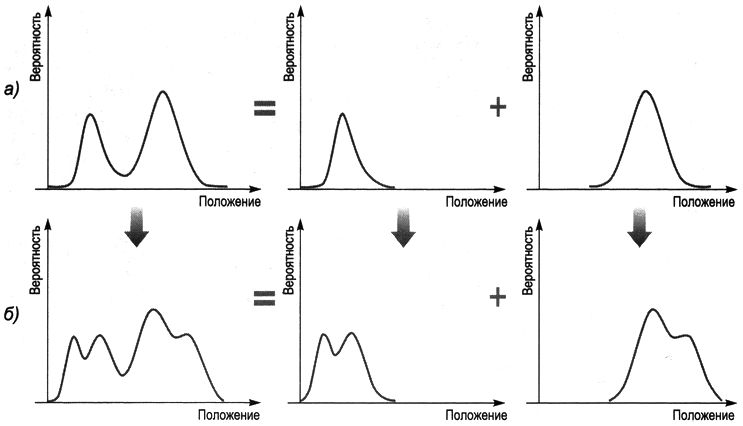
Рис. 8.8. а ) Исходную волну возможности возможно разложить в комплект из двух волн с более несложными формами; б ) Распространение исходной волны возможности возможно воспроизвести, в случае, если раздельно разглядеть эволюцию более несложных волн и после этого объединить полученные результаты
Это может смотреться как технический нюанс, но линейность есть поразительно замечательным математическим свойством. Она разрешает претворять в судьбу очень важную стратегию «разделяй и властвуй». В случае, если исходная форма волны сложна, её легко возможно поделить на более простые фрагменты и проанализировать любой по отдельности. В итоге все полученные результаты складываются совместно. В действительности, при анализе опыта с двойной щелью (рис. 8.4) мы уже виделись с одним ответственным применением линейности. Задача определения распространения волны возможности электрона была разбита на пара этапов: вначале мы увидели, как фрагмент волны проходит через левую щель, после этого через правую щель, по окончании чего мы сложили две оказавшиеся волны. Конкретно так мы нашли известную интерференционную картину. взглянуть на исписанную формулами доску в кабинете у эксперта по квантовой физике, вы определите этот подход.
Но линейность не только осуществляет контроль квантовые вычисления; она кроме этого порождает трудности теории при объяснении того, что происходит на протяжении измерения. оптимальнее это можно понять, используя линейность к самому акту измерения.
Представьте, что сейчас вы экспериментатор и с громадной ностальгией вспоминаете ваше детство в Нью-Йорке, исходя из этого, занимаясь измерением положений электронов, вы впрыскиваете их в миниатюрную настольную модель города. Вы начинаете опыт с одного электрона, волна возможности которого имеет особенно несложную форму — в виде красивого пика, как на рис. 8.9, что показывает на практически 100-процентную возможность, что сейчас электрон находится на углу тридцать четвёртой улицы и Бродвея. (Не волнуйтесь о том, как у электрона была конкретно такая форма волны возможности, принимайте её так, как имеется.[26]) В случае, если именно сейчас вы измеряете положение электрона посредством весьма хорошего детектора, то полученный итог будет весьма правильным, и на мониторе детектора должно показаться «Угол тридцать четвёртой улицы и Бродвея». Вправду, в случае, если совершить таковой опыт, то итог будет конкретно таким (рис. 8.9).

Рис. 8.9. Волна возможности электрона в определённый момент имеет пик на углу Тридцать четвёртой улицы и Бродвея. Измерение положения электрона в тот момент подтверждает тот факт, что электрон находится в том месте, где у волны имеется пик
Я думаю, будет весьма сложно разобраться в том, как уравнение Шрёдингера вмешивает волну возможности этого электрона в волну возможности около триллиона триллионов атомов, из которых состоит детектор, побуждая всю эту огромную совокупность каким-то образом организоваться и выдать на монитор «Угол тридцать четвёртой улицы и Бродвея», и кто бы не выстроил данный детектор, он задал нам тяжёлую задачку. Детектор устроен так, что при сотрудничестве с таким электроном на мониторе появляется сообщение о единственном определённом положении, в котором сейчас времени находится электрон. Если бы в таковой ситуации детектор выдал что-нибудь второе, то его следовало бы заменить на новый, трудящийся как положено. Само собой разумеется, на пересечении Тридцать четвёртой улицы и Бродвея нет ничего особого, ну не считая разве магазина «Macy’s»; в случае, если совершить такой же опыт с волной возможности электрона, имеющей пик в планетарии Хейден рядом с восемьдесят первой улицей и Сентрал Парк Вест авеню либо в офисе Билла Клинтона на 125-й улице рядом с Ленокс авеню, монитор детектора отобразит заглавия конкретно этих мест.
Сейчас давайте разглядим чуть более сложный профиль волны (рис. 8.10). Эта волна возможности показывает на то, что сейчас времени имеется два места вероятного нахождения электрона — Земляничные поля (мемориал Джона Леннона в Центральном парке) и мемориал Гранта в Риверсайд парке. (Сейчас у электрона мрачное настроение.) В случае, если мы измеряем положение электрона, но не следуем Бору и, придерживаясь самые точных опытов, предполагаем, что уравнение Шрёдингера есть применимым — к частицам и электрону, из которых состоит детектор, по большому счету ко всему, — то что тогда появится на мониторе детектора? Ключ к ответу в линейности. Нам как мы знаем, что происходит при измерении отдельных волн с одним пиком. Уравнение Шрёдингера заставляет монитор детектора сказать нам положение пика (рис. 8.9). Тогда из линейности направляться, что для нахождения ответа для волны с двумя пиками направляться объединить результаты измерений каждого пика в отдельности.

Рис. 8.10. Волна возможности электрона имеет пик в двух местах. Линейность уравнения Шрёдингера говорит, что измерение положения электрона приведёт к смешению двух положений
Конкретно тут появляются кое-какие странности. На первый взгляд, совокупный итог подразумевает, что монитор детектора обязан в один момент зарегистрировать положения двух пиков. Как на рис. 8.10, слова «Земляничные поля» и «мемориал Гранта» должны вспыхнуть в один момент, накладываясь приятель на втором, как на экране зависшего компьютера. Уравнение Шрёдингера кроме этого обрисовывает, как волны возможности фотонов, испущенных монитором детектора, спутываются с волнами частиц, из которых состоят колбочки и палочки в сетчатке вашего глаза, и после этого распространяются по нейронам, порождая зрительный образ того, что вы видите. В предположении неограниченной господстве уравнения Шрёдингера, линейность применима и тут, исходя из этого не только монитор детектора продемонстрирует сходу оба положения электрона, вместе с тем ваше сознание окажется в ступоре, полагая, что электрон в один момент находится в двух местах.
Для более сложных волновых профилей путаница делается ещё больше. От волны с четырьмя пиками голова ещё больше идёт кругом. С шестью ещё хуже. Увидим, что в случае, если добавлять волновые пики разной высоты в различных местах на модели Манхэттена, их совместная форма обрисует простой, тихо изменяющийся волновой профиль, как схематично нарисовано на рис. 8.11. Свойство линейности так же, как и прежде выполняется, и это указывает, что итоговая надпись на мониторе, и окончательное состояние вашего сознания и ментальный образ определяются объединением результатов, взятых от каждого пика в отдельности. Детектор обязан в один момент регистрировать положения всех пиков без исключения — каждой точки Манхэттена, — приводя ваше сознание в полнейшее замешательство, не имея никакой возможности выделить единственное определённое положение электрона.93

Рис. 8.11. Неспециализированная волна возможности есть объединением многих волн с одним пиком, любая из которых соответствует вероятному положению электрона
Непременно, такое положение дел никак не согласуется с нашим опытом. Никакой нормально трудящийся детектор при проведении измерения не выведет конфликтующих между собой результатов. Ни у одного обычного человека, делающего это измерение, не появляется в голове головокружительной смеси одновременных, но одвременно с этим различных, результатов.
Сейчас вы осознаёте привлекательность идеи Бора. Примите пилюлю от головокружения, дал совет бы он. В соответствии с Бору, мы не видим противоречивых показаний детектора, в силу того, что они не происходят. Согласно его точке зрения, мы пришли к неправильному заключению, в силу того, что переоценили применимость уравнения Шрёдингера для громадных объектов — для лабораторного оборудования, на котором производятся измерения, и учёных, фиксирующих результаты. Не смотря на то, что уравнение Шрёдингера и его свойство линейности говорят, что нужно объединять результаты разных вероятных финалов (и тогда ничего не схлопывается), Бор говорит, что это неверно, в силу того, что акт измерения задвигает уравнение Шрёдингера за штору. Вместо этого, заявляет Бор, акт измерения заставляет все пики на рис. 8.10 либо 8.11, не считая одного, сколлапсировать в ноль; возможность выживания какого-либо одного конкретного пика пропорциональна его высоте. Данный единственный оставшийся пик задаёт единственное показание детектора, и распознаётся вашим сознанием как единственный итог. С головокружением совладали.
Но для Эверетта, а позднее для ДеВитта, цена за такую идею Бора была через чур высока. Уравнение Шрёдингера было придумано для описания частиц. Всех частиц. Так отчего же оно каким-то образом не применимо к частным конфигурациям частиц — тем, из которых состоит экспериментальное оборудование, и тем, из которых состоят те, кто снимает с него показания? Это легко бессмысленно. Исходя из этого Эверетт внес предложение не отказываться от уравнения Шрёдингера так скоро. Напротив, он внес предложение проанализировать, куда нас приведёт уравнение Шрёдингера, отталкиваясь от принципиально второй точки зрения.
Множественность миров
Но мы сходу окажемся в затруднительной ситуации, в случае, если постараемся думать, словно бы измерительный прибор либо сознание человека способны в один момент принимать различные действительности. Такие мысли заводят в тупик. У нас смогут быть противоречивые мнения о том либо о сём, мы можем испытывать смешанные чувства о различных людях, но в то время, когда речь идет о фактах, образующих окружающую реальность, всё, что мы знаем, свидетельствует в пользу однозначного и объективного описания. Всё, что нам известно, показывает, что один одно измерение и прибор дадут один итог; а один итог и один ум приведут к одному умственному заключению.
Мысль Эверетта была в том, что уравнение Шрёдингера, математическая база квантовой механики, согласуется с таким опытом. А обстоятельство кажущейся неоднозначности в умственных заключениях и показаниях детектора коренится в методе отечественного анализа этих математических вычислений — другими словами в том, как мы объединяем результаты измерений, продемонстрированных на рис. 8.10 и рис. 8.11. Давайте остановимся на нём подробнее.
Если вы измеряете волну с единственным пиком, как на рис. 8.9, детектор регистрирует расположение пика. В случае, если пик находится в Земляничных полях, то детектор продемонстрирует это место; если вы взглянуть на полученный итог, ваше сознание зафиксирует это место и у вас отложится эта информация. В случае, если пик находится в мемориале Гранта, то детектор продемонстрирует это место; если вы взглянуть на полученный итог, ваше сознание зафиксирует это место и у вас отложится эта информация. При измерении волны с двойным пиком (рис. 8.10), уравнение Шрёдингера требует объединить два только что взятых результата. Но, говорит Эверетт, будьте наряду с этим внимательны и бдительны. Комбинированный итог не пребывает в том, что сознание и детектор любой в один момент зафиксирует два положения. Так думать неверно.
Напротив, рассуждая практически и последовательно, мы приобретаем комбинированный итог в таком виде: сознание и детектор фиксируют Земляничные поля и сознание и детектор фиксируют мемориал Гранта. Что бы это означало? Сперва я обрисую ответ только в общем, а подробности растолкую позднее. Дабы соответствовать идее Эверетта, детектор, вы и всё другое обязано расщепиться при измерении, образуя две копии детектора, две копии вас и две копии всего остального, а единственное различие между копиями будет в том, что одна копия детектора и одна копия вас зафиксируют Земляничные поля, а вторая другая копия и копия детектора вас зафиксируют мемориал Гранта. Как продемонстрировано на рис. 8.12, это указывает, что сейчас имеется две параллельные действительности, два параллельных мира. Для каждой копии вас, находящейся в каждом из миров, проводимое умственное заключение и измерение довольно взятого результата представляется правильным и единственным, что соответствует привычному течению судьбы. Конечно же, особенность в том, что вас сейчас двое.

Рис. 8.12. В картине Эверетта, в случае, если волна возможности частицы имеет два пика, то измерение ведет к двум итогам. В одном мире частица находится в первом положении; в другом мире частица находится во втором положении
Для наглядности я разглядел измерение положения единственной частицы, волна возможности которой особенно несложна. Но мысль Эверетта применима в более широком контексте. При измерении положения частицы, волна возможности которой имеет произвольное число пиков, к примеру, пять пиков, будет пять параллельных действительностей, отличающихся друг от друга лишь различными расположениями частиц, регистрируемыми детекторами в каждой действительности и сознанием каждого из вас в каждой действительности. В случае, если один из этих пятикратных вас займётся измерением положения второй частицы, волна которой имеет семь пиков, то вы и тот мир опять расщепятся ещё на семь миров, по одному на любой вероятный итог. В случае, если совершить измерения волны, как на рис. 8.11, которую возможно разбить на огромное количество близко расположенных пиков, то в следствии появится огромное количество параллельных действительностей, в каждой из которых каждое вероятное положение частицы будет зафиксировано детектором и прочтено вашей копией. В подходе Эверетта каждое квантово-механически возможное событие, другими словами такое, возможность которого хороша от нуля, находит собственную реализацию в собственном отдельном мире. Это и имеется множество миров в многомировом подходе к квантовой механике.
В случае, если возвратиться к терминологии прошлых глав, такое множество миров направляться обрисовать как мультивселенную, составленную из множества вселенных. Она будет шестой по счёту. Я буду именовать её квантовой мультивселенной .
История о двух историях
Обрисовывая, как квантовая механика может порождать множественные действительности, я применял глагол «расщепляться». Его применял Эверетт. Кроме этого поступал и ДеВитт. Но я признаю, что в данном контексте данный глагол может сбивать с толку, и я колебался, стоит ли его применять. Но всё-таки поддался искушению. В собственное оправдание сообщу, что время от времени более действенно забрать кувалду, дабы пробить дыру в барьере, стоящем между нами и необыкновенной догадкой об устройстве действительности, по окончании чего заделать рванные края, чем бережно вырезать безукоризненное окно, через которое раскрывается новая возможность. Я решил воспользоваться таковой кувалдой, и сейчас в этом и следующем разделах будет произведён нужный ремонт. Кое-какие идеи чуть более сложны, чем те, с которыми мы уже познакомились, и цепочка изложений чуть более долга, чем раньше, но я призываю вас набраться терпения. Мне приходилось сталкиваться с тем, что обычно у людей, каковые что-то слышали о многомировом подходе либо кроме того как-то с ним привычны, было чувство, что он основан на очень экстравагантных умозрительных построениях. Но ничего аналогичного. Как я растолкую позднее, многомировой подход есть, в некоем смысле, самый консервативным методом осмысления квантовой физики, и принципиально важно осознать, по какой причине это так.
Принципиально важно осознать, что физикам постоянно приходится говорить истории с двух сторон. Одна сторона история — математическая — о том, как вселенная начинается в соответствии с данной теории. Вторая история — физическая, которая переводит абстрактные математические термины на экспериментальный язык. Вторая история обрисовывает то, как математическая эволюция видится таким наблюдателям, как мы с вами, и, в более неспециализированном смысле, что математические знаки теории говорят нам о природе действительности.94 Во времена Ньютона эти две истории в общем и целом были аналогичны, как я отмечал в главе 7, в то время, когда сказал о осязаемости и непосредственности ньютоновской «архитектуры». Любой математический знак в уравнениях Ньютона имеет прямой и очевидный физический аналог. Знак x ? О, это положение мяча. Знак ? ? Скорость мяча. Но в то время, когда мы переходим к квантовой механике, перевод математических знаков в замечаемые явления окружающего нас мира оказывается не столь несложным. Более того, применяемый понятия и язык, нужные для двух историй, становятся столь хорошими, что вам требуется отлично разобраться с каждой. Но принципиально важно разделять, что имеется что: описания и какие идеи привлекаются как часть фундаментальной математической структуры теории, а какие конкретно употребляются для установления связи с людской опытом.
Давайте послушаем эти две истории при многомирового подхода к квантовой механике. Вот первая из них.
Математический аппарат многомирового подхода, в отличие от копенгагенского, ясен, прозрачен и неизменен. Уравнение Шрёдингера определяет распространение во времени волн возможности и ни при каких обстоятельствах не задвигается за штору; оно в любой момент при деле. Уравнение Шрёдингера направляет форму волн возможности, заставляя их с течением времени смещаться, видоизменяться и колебаться. Определяем ли мы волну возможности частицы либо совокупности частиц либо разглядываем разные ансамбли частиц, составляющие вас либо ваше измерительное оборудование, уравнение Шрёдингера берёт исходную форму волны возможности в качестве начальных данных и подобно графической программе, управляющей замысловатой экранной заставкой, выдаёт волновой профиль в любой последующий момент времени. В соответствии с этому подходу, конкретно так начинается вселенная. На этом всё. Финиш истории. Правильнее, финиш первой истории.
Напомним, что при изложении первой истории я не применял ни слово «расщепляться», ни понятия «множество миров», «параллельные вселенные» либо «квантовая мультивселенная». Многомировой подход не испытывает недостаток в этих догадках. Они не играются никакой роли в фундаментальной математической структуре теории. Но, как мы на данный момент заметим, эти идеи будут призваны во второй истории, в то время, когда, следуя Эверетту и его последователям, расширившим его пионерские результаты, мы изучаем, как математика растолковывает нам то, что мы замечаем и измеряем.
Давайте начнём с несложного — либо так несложного, как окажется. Допустим, мы измеряем положение электрона, волна возможности которого имеет один пик (рис. 8.9). (Опять-таки, не волнуйтесь о том, по какой причине у электрона конкретно такая форма волны возможности — принимайте это как данность.) Как я уже сказал, нам не под силу подробно изложить первую историю кроме того для того чтобы несложного измерительного процесса. Для этого потребовалось бы посредством уравнения Шрёдингера выяснить, как волна возможности, обрисовывающая положения огромного количества частиц, составляющих вас и ваш измерительный прибор, объединяется с волной возможности электрона и как это объединение эволюционирует во времени. Мои студенты, многие из которых очень талантливые, часто не смогут решить уравнение Шрёдингера кроме того для одной частицы. Вы и детектор состоите приблизительно из 1027 частиц. Решить математически уравнение Шрёдингера для для того чтобы громадного количества составляющих фактически невозможно. Но мы как следует воображаем результирующую картину. При измерении положения электрона массы частиц приходят в перемещение. Приблизительно 1027 частиц монитора детектора, подобно танцорам в отлично поставленном шоу, торопятся занять собственные места, дабы разом высветить «Угол тридцать четвёртой улицы и Бродвея», а приблизительно такое же количество частиц в моих голове и глазах делают всё нужное для чёткого восприятия информируемого результата. Уравнение Шрёдингера, каким бы неподъёмным ни был правильный анализ для столь огромного количества частиц, обрисовывает конкретно такое перемещение.
Представить наглядно это преобразование на уровне волны возможности кроме этого нереально. На рис. 8.9 и других ему аналогичных я применял сетку из двух координатных осей, ведущих с севера на юг и с востока на запад, дабы обозначить вероятные положения одной частицы на модели Манхэттена. Значения волны возможности в каждом положении соответствовали высоте волны. Это уже есть упрощением, в силу того, что я не применял третью ось, положение частицы по вертикали (где находится частица — на втором этаже «Macy’s» либо на пятом). Я не имел возможности применять вертикальную ось, в силу того, что в противном случае не осталось бы осей для отображения высоты волны. Таковы ограничения отечественного зрительной системы и головного мозга, каковые в следствии эволюции принимают лишь три пространственных измерения. Для верного изображения волны возможности примерно 1027 частиц нам потребуется ввести по три оси для каждой, дабы математически обрисовать каждое вероятное положение, которое может занять любая из частиц.[27]Добавление кроме того одной вертикальной оси на рис. 8.9 затруднит его восприятие; добавление ещё миллиарда миллиардов лишает картину по большому счету какого-либо смысла.
Но крайне важно иметь наглядный образ всех главных идей; исходя из этого давайте постараемся, осознавая, что итог будет далёк от совершенства. При описании волны возможности частиц, из которых состоите вы и ваш детектор, я буду придерживаться варианта с двумя осями на плоскости, но наряду с этим применять непривычную интерпретацию этих осей. Грубо говоря, я буду вычислять, что любая ось представляет собой громадный пучок осей, хорошо сгруппированных между собой, каковые символически изображают вероятные положения для того чтобы же огромного количества частиц. Так, волна, изображённая посредством таких осей-пучков, будет обрисовывать возможности расположений огромного комплекта частиц. Дабы выделить отличие между одночастичной и многочастичной обстановками, волна возможности многочастичного комплекта будет иметь светящийся контур (рис. 8.13).

Рис. 8.13. Схематичное изображение комбинированной волны возможности для всех частиц, составляющих вас и детектор
Одночастичная и многочастичная иллюстрации имеют кое-какие неспециализированные особенности. Подобно волне с одним пиком (рис. 8.6), которая задаёт быстро скошенную возможность (практически 100 процентов в области пика и практически 0 процентов во всех остальных местах), остроконечная волна (рис. 8.13) кроме этого обозначает очень сильно скошенную возможность. Но направляться осторожничать , в силу того, что познание, основанное на одночастичной модели, может сыграть с вами злую шутку. К примеру, глядя на рис. 8.6 конечно думать, что рис. 8.13 соответствует частицам, каковые все скопились в одном месте. Но это не верно. Остроконечный вид волны на рис. 8.13 символизирует, что начальное состояние каждой из частиц, составляющих вас, и каждой из частиц, из которых составлен ваш детектор, есть простым, привычным состоянием, в то время, когда положение определяется с практически 100-процентной возможностью. Но не все частицы находятся в одном месте. Частицы из которых состоят ваши рука, голова и плечо наверняка сгруппированы в том месте, где находятся ваши рука, плечо либо голова; частицы, составляющие ваш измерительный прибор, наверняка сгруппированы в том месте, где находится ваш прибор. Остроконечный волновой профиль на рис. 8.13 свидетельствует, что любая из этих частиц имеет малый шанс быть найденной где-либо в другом месте.
В случае, если сейчас выполнить измерение, продемонстрированное на рис. 8.14, то многочастичная волна возможности (для частиц, из которых состоите вы и ваш детектор) из-за сотрудничества с электроном начнёт распространяться (как схематически продемонстрировано на рис. 8.14а ). Все вовлечённые в данный процесс частицы всё ещё находятся вблизи определённых положений (в вас, в детектора), исходя из этого волна на рис. 8.14а сохраняет остроконечный профиль. Но происходит массовое перераспределение частиц, которое ведет к фразе «Земляничные поля» на мониторе детектора, а также в вашей голове (рис. 8.14б ). Рис. 8.14а иллюстрирует математическое преобразование, определяемое уравнением Шрёдингера, соответствующее истории первого типа. Рис. 8.14б иллюстрирует физическое описание данной математической эволюции, что соответствует истории второго типа. Подобно, в случае, если осуществить опыт, продемонстрированный на рис. 8.15, то случится подобное смещение (рис. 8.15а ). Данное смещение соответствует массовому перераспределению частиц, которое ведет к фразе «Мемориал Гранта» на мониторе детектора и порождает в вашей голове соответствующий образ (рис. 8.15б ).

Рис. 8.14а . Схематическая иллюстрация эволюции комбинированной волны возможности всех частиц, составляющих вас и ваш детектор, определяемой уравнением Шрёдингера, при измерении положения электрона. Волна возможности самого электрона имеет пик на Земляничных полях

Рис. 8.14б . Соответствующая физическая (экспериментальная) история

Рис. 8.15а . Тот же самый тип математической эволюции, как и на рис. 8.14а , но волна возможности электрона имеет пик на мемориале Гранта
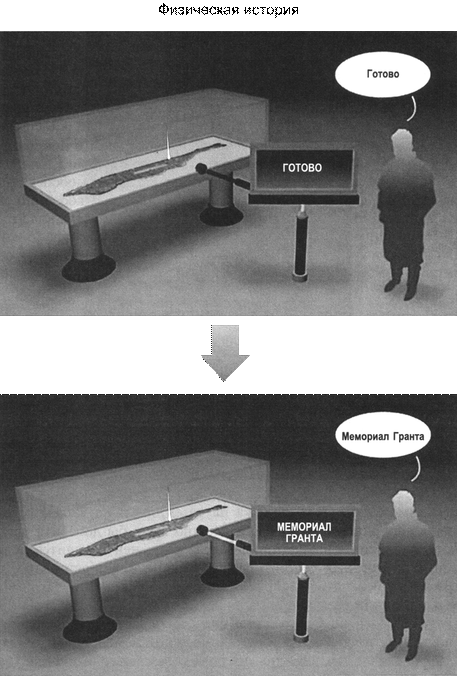
Рис. 8.15б . Соответствующая физическая (экспериментальная) история
Сейчас воспользуемся линейностью и соединим два результата воедино. При измерении положения электрона, волна возможности которого имеет два пика, волна возможности частиц, из которых состоите вы и детектор, смешивается с волной электрона, что ведет к эволюции, продемонстрированной на рис. 8.16а — объединённой эволюции, изображённой на рис. 8.14а и 8.15а . До тех пор пока что это не более чем иллюстрированная и прокомментированная версия квантовой истории первого типа. Мы стартуем от волны возможности с заданной формой, потом она эволюционирует во времени как предписывает уравнение Шрёдингера, и в следствии появляется волна возможности с новой формой. Давайте, опуская подробности, изложим эту математическую историю не количественным, а качественным языком истории второго типа.
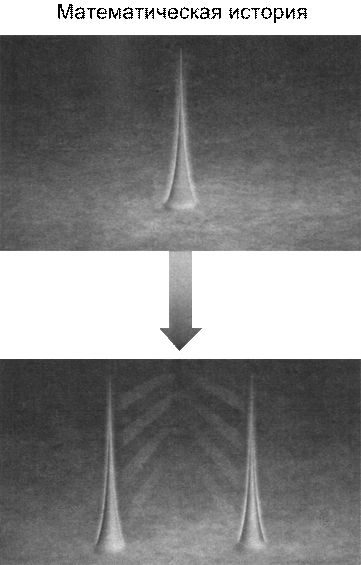
Рис. 8.16а . Схематическая иллюстрация эволюции комбинированной волны возможности всех частиц, составляющих вас и ваш детектор, определяемой уравнением Шрёдингера, при измерении положения электрона, волна возможности которого имеет два пика
С физической точки зрения, любой пик на рис 8.16а соответствует конфигурации огромного числа частиц, появляющейся в детекторе, на мониторе которого высвечивается определённая информация, принимаемая вашим сознанием. Левому пику соответствует «Земляничные поля», а правому «Мемориал Гранта». Также различия, нет ничего , что отличало бы один пик от другого. Я подчёркиваю это, в силу того, что необходимо понимать, что ни один из них не есть более настоящим, чем второй. Ничего, не считая информации на мониторе вашего прочтения и детектора данной информации, не отличает два пика многочастичной волны возможности.
Это указывает, что отечественная история второго типа, как продемонстрировано на рис. 8.16б , вовлекает две действительности.

Рис. 8.16б . Соответствующая физическая (экспериментальная) история
В действительности, фокусировка на детекторе и на вашем сознании есть ещё одним упрощением. Возможно было бы добавить частицы, из которых состоит лаборатория и всё, что в ней находится, и частицы, из которых состоит Почва, всё остальное и Солнце, и все рассуждения остались бы прошлыми, практически дословными. Единственное различие в том, что светящийся профиль волны возможности на рис. 8.16а сейчас будет кроме этого содержать данные о всех таких частицах. Но потому, что обсуждаемое нами измерение не оказывает в действительности на них влияния, их роль совсем вторична. Но будет полезно учесть эти частицы, в силу того, что отечественную историю второго типа возможно увеличить и включить не только вашу копию, колдующую над детектором, что проводит измерение, вместе с тем копии вашей лаборатории, всего остального на Земле, вращающейся по орбите около Солнца, и без того потом. Это указывает, что любой пик в истории второго типа соответствует тому, что мы традиционно назвали бы настоящей вселенной. В одной таковой вселенной на мониторе детектора вы видите «Земляничные поля», в второй — «Мемориал Гранта».
В случае, если исходная волна возможности электрона имеет, скажем, четыре пика, либо пять, либо сто, либо любое второе число, случится то же самое: волновая эволюция приведёт к четырём, либо пяти, либо сотне, либо к любому второму числу вселенных. В самом неспециализированном случае, как на рис. 8.11, размазанная волна имеет пик в каждой точке, и исходя из этого волновая эволюция ведет к огромному комплекту вселенных, по одной на каждое вероятное положение.95
Но, как было указано, единственное, что происходит в любом из этих сценариев, содержится в том, что волна возможности подставляется в уравнение Шрёдингера, потом в работу включается математика, и на выходе получается волна с поменянным профилем. Нет никакого «клонирующего механизма». Нет никакого «расщепляющего механизма». Конкретно исходя из этого я сообщил ранее, что такие слова смогут запутать читателя. Нет ничего не считая вероятностно-волнового «механизма», что управляется сухими математическими законами квантовой механики. В то время, когда результирующая волна принимает конкретный профиль, к примеру, продемонстрированный на рис. 8.16а , мы пересказываем математическую историю на языке второго типа, и делается вывод, что каждому пику соответствует учёное разумное существо, находящееся в простой вселенной, с уверенностью замечающее только один определённый итог в заданном опыте (рис. 8.16б ). Если бы существовал метод опросить всех этих учёных существ, то выяснилось бы, что любой из них — это правильная копия вторых. Единственная отличие будет в том, что все они будут замечать различные определённые результаты.
А потому, что Копенгагенская школа и Бор обосновывали, что лишь одна из этих вселенных существует (в силу того, что акт измерения, что, по их утверждению, не описывается уравнением Шрёдингера, приведёт к коллапсу всех остальных вселенных), и потому, что первый ход в попытке выйти за рамки концепции Бора и увеличить применимость уравнения Шрёдингера ко всем частицам, включая те, из которых состоит экспериментальное оборудование и мозг , привёл к немыслимой путанице (в силу того, что данное устройство либо мозг, должны, по-видимому, воспринять все вероятные результаты в один момент), Эверетт заключил , что более внимательная трактовка уравнения Шрёдингера может дать что-то второе: широкую действительность, складывающуюся из всевозрастающего числа вселенных.
Препринт статьи Эверетта 1957 года был разослан последовательности физиков в мире до публикации главной статьи. По требованию Уилера изложение было так урезано, что многие, кто просматривал его, не были уверены, вправду ли Эверетт думает, что все вселенные в его математическом подходе настоящи. Эверетт определил об данной неясности и решил разъяснить обстановку. В «примечаниях при корректуре», каковые он, по-видимому, написал прямо перед публикацией и, вероятнее, не уведомляя об этом Уилера, Эверетт чётко выразил собственную позицию относительно природы различных квантово-механических результатов: «С позиций теории, все… являются “настоящими”, ни одна из них не более “настояща”, чем все остальные».96