В данной статье мы поболтаем о том, что такое квадратичная функция, обучимся строить ее график и определять вид графика в зависимости от знака старшего и знака дискриминанта коэффициента.
Итак.
Функция вида , где именуется квадратичной функцией.
В уравнении квадратичной функции:
a — старший коэффициент
b — второй коэффициент
с — вольный участника.
Графиком квадратичной функции есть квадратичная парабола, которая для функции имеет форму:
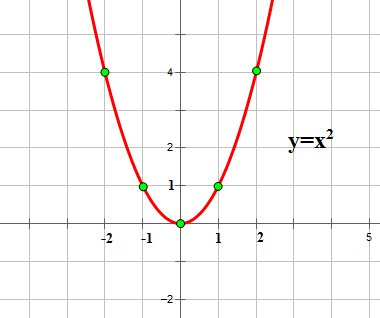
Обратите внимание на точки, обозначенные зелеными кружками — это, так именуемые базисные точки. Дабы отыскать координаты этих точек для функции , составим таблицу:
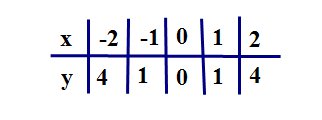
Внимание! В случае, если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции при любых значениях остальных коэффициентов.
График функции имеет форму:
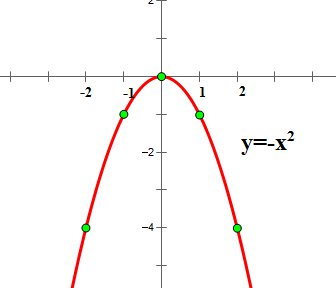
Для нахождения координат базисных точек составим таблицу:
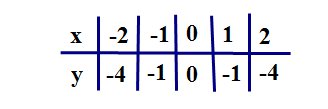
Обратите внимание, что график функции симметричен графику функции относительно оси ОХ.
Итак, мы увидели:
В случае, если старший коэффициент a0, то ветви параболы напрaвлены вверх.
В случае, если старший коэффициент a
Второй параметр для построения графика функции — значения х, в которых функция равна нулю, либо нули функции. На графике нули функции — это точки пересечения графика функции с осью ОХ.
Потому, что ордината (у) любой точки, лежащей на оси ОХ равна нулю, дабы отыскать координаты точек пересечения графика функции с осью ОХ, необходимо решить уравнение .
При квадратичной функции необходимо решить квадратное уравнение .
Сейчас внимание!
В ходе ответа квадратного уравнения мы находим дискриминант: , что определяет число корней квадратного уравнения.
И тут вероятны три случая:
1. В случае, если ,то уравнение не имеет ответов, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. В случае, если ,то график функции выглядит как-то так:
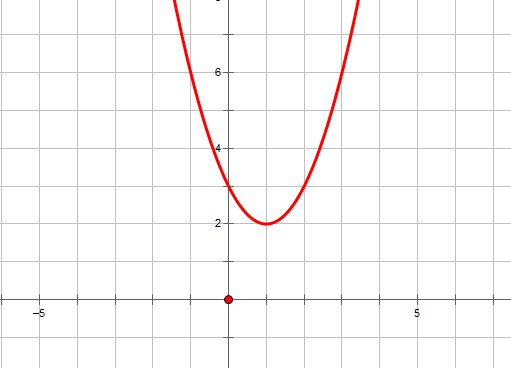
2. В случае, если ,то уравнение имеет одно ответ, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. В случае, если ,то график функции выглядит приблизительно так:
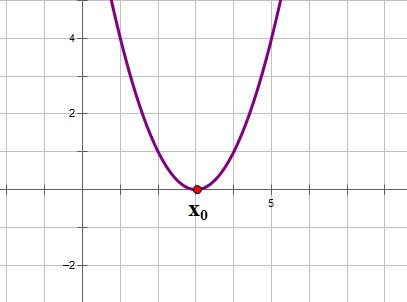
3. В случае, если ,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:
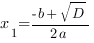 ,
, 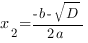
В случае, если ,то график функции выглядит приблизительно так:
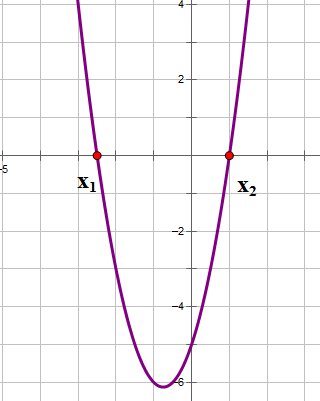
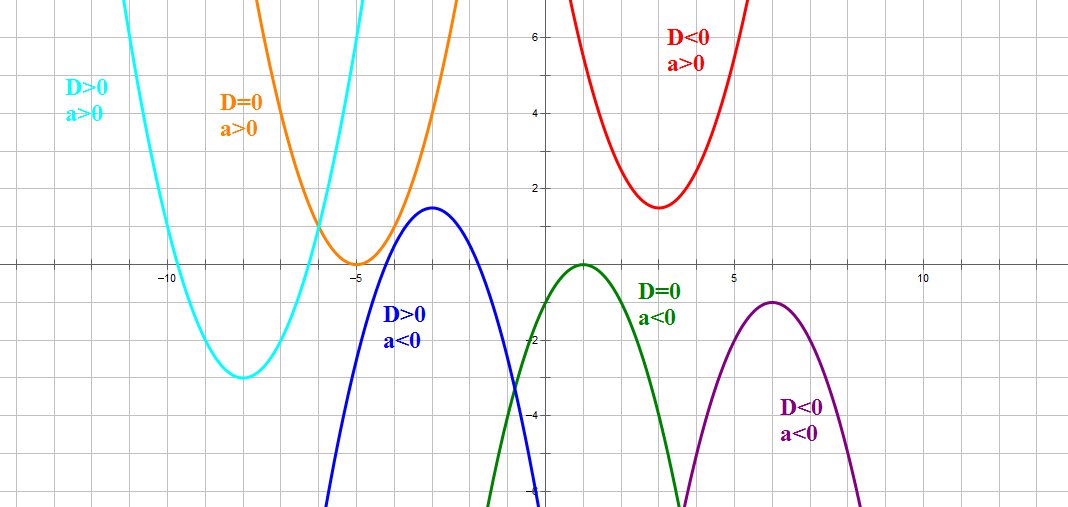
Следовательно, зная знак ветвей дискриминанта и направление параболы, мы уже можем в общем выяснить, как выглядит график отечественной функции.
Следующий серьёзный параметр графика квадратичной функции — координаты вершины параболы:
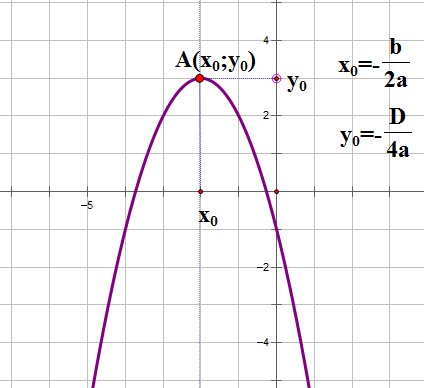
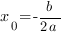
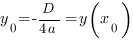
Прямая, проходящая через вершину параболы параллельно оси OY есть осью симметрии параболы.
И еще один параметр, нужный при построении графика функции — точка пересечения параболы с осью OY.
Потому, что абсцисса любой точки, лежащей на оси OY равна нулю, дабы отыскать точку пересечения параболы с осью OY, необходимо в уравнение параболы вместо х подставить ноль: .