Из анализа размеров скорости образования роста и скорости зародышей кристаллов направляться, что эти характеристики имеют два серьёзных особенности. Во-первых, они в любой момент конечны по величине. Во-вторых, при уменьшении температуры благодаря роста кинетических затруднений, значения скоростей роста зародышеобразования и их предстоящего роста уменьшаются до нуля. Следовательно, их произведение, характеризующее долю закристаллизованного количества, также имеет конечную величину и в области низких температур преобразовывается в ноль. Это значит, что для любого вещества возможно подобрать такую скорость охлаждения, при которой при охлаждения до безотносительного нуля в расплаве появится кристаллическая фаза, объемная часть которой будет заведомо меньше какой-либо наперед заданной величины. Как указывалось выше, в случае, если охлаждать жидкость, которая владеет стеклообразующей свойством, от температуры, равной температуре плавления, до температуры Т, которая лежит ниже температуры стеклования Тg с таковой скоростью q, что в единице количества появляется всего один центр кристаллизации (Nk =1), то полученное так вещество практически не будет содержать кристаллических включений и по существу будет стеклообразным. В этом случае скорость q, введенная физически строго, не может быть конкретно сопоставлена с результами экспериментов.
Фактически для экспериментальных исследований и анализа применяют величину критической скорости охлаждения как минимальной скорости охлаждения расплава от температуры плавления, при которой в жидкости объемная часть кристаллической фазы не превышает некоего наперед заданного значения. В первый раз данный подход применил Улманн для расчета критической скорости охлаждения.
Для расчета критической скорости охлаждения по Улманну возможно воспользоваться уравнением Колмогорова – Аврами для зависимости доли закристаллизованного количества от времени в упрощенном виде (18). Пускай часть закристаллизованного количества равна 10-6, что в стеклообразном материале экспериментально не определяется и считается, что материал кристаллических включений не содержит.
По уравнению (18) возможно вычислить для каждой температуры время, за который в переохлажденной жидкости образуется указанное выше количество кристаллической фазы. При подстановке численных значений в уравнение (18), получается следующее выражение:
t = 34 [? I (T) u3(T)]1/4.
Полученные размеры возможно отложить на зависимости температура – время (рис.8). Кривая на рис.8, напоминающая по форме шнобель, именуется Т – t — ? кривой. Точки, лежащие в кривой, соответствуют условиям выдержки, при которых в примере вырастает кристаллическая фаза, объемная часть которой более заданной величины 10-6. Линейному режиму охлаждения от температуры плавления отвечает прямая (см. рис.8).
Разумеется, что для касательной к Т — t — ? кривой, выходящей из точки Тпл, выполняется условие ? 10-6. Скорость охлаждения, соответствующая данной прямой, и есть критической скоростью охлаждения для данной доли кристаллической фазы.
Преимущество представленного способа пребывает в его наглядности и простоте. Но, далеко не в любых ситуациях полученные результаты удовлетворительно согласуются с опытом, даже в том случае, если наперед заданная величина объемной доли закристаллизованной фазы существенно увеличена (к примеру, до 5%).
Как пример возможно разглядеть эти по критическим скоростям охлаждения халькогенидов мышьяка (табл.1).
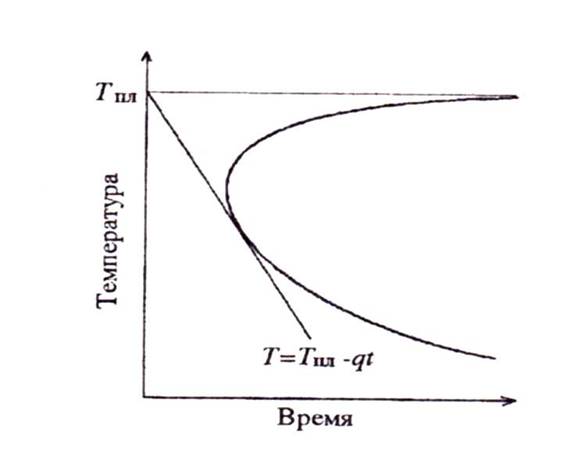
Рис.8. Неспециализированный вид Т — t — ? диаграммы.
Таблица 1. Критические скорости охлаждения халькогенидов мышьяка.
| Соединение | Тпл, К | Критическая скорость охлаждения, К/с | |||
| по (18) | ?=10-6 по (21) | ?=0.05 по (21) | Опыт | ||
| As2O3 | 1.4.10-4 | 2.7.10-5 | 1.8.10-6 | 2.10-5 | |
| As2S3 | 3.1.10-4 | 3.9.10-5 | 2.6.10-6 | 2.10-5 | |
| As2Se3 | 0.44 | 5.1.10-2 | 3.4.10-3 | (9±2).10-3 | |
| As2Te3 | 4.2 | 28±3 |
Главная причина для того чтобы несоответствия содержится в автоматическом переносе результатов расчета скорости кристаллизации при изотермическом отжиге на неизотермический режим настоящего охлаждения примера. Более точный способ оценки критической скорости охлаждения должен быть основан расчетах по обобщенному уравнению Колмогорова – Аврами, которое для неизотермических условий (т.е. в то время, когда I и u являются функциями времени) возможно записано в следующем виде:
?(t) = 1 — exp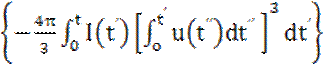 
. (20)
Для случая линейного охлаждения со скоростью q в уравнении (20) время возможно заменено на температуру и тогда
?(Т) = 1 — exp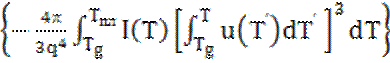 
. (21)
Применяя уравнение (21), возможно отыскать скорость охлаждения q, при которой часть кристаллической фазы в стекле будет равна некоей наперед заданной величине (к примеру, 5%). В табл.1 представлены величины вычисленных так критических скоростей охлаждения халькогенидов мышьяка.
Экспериментально критическую скорость охлаждения находят при охлаждении расплава с определенной скоростью; наряду с этим по ходу охлаждения конкретно исследуется процесс кристаллизации расплава, или наличие кристаллической фазы определяется в примере по окончании охлаждения. Для примера на рис. 9 приведены концентрационные зависимости критических скоростей охлаждения в трех халькогенидных совокупностях. Видно, что максимуму критических скоростей охлаждения соответствуют составы соединений, плавящихся конгруэнтно (с открытым максимумом). Кроме этого характерной изюминкой есть уменьшение критической скорости охлаждения при приближении состава к эвтектическому. На основании изложенного выше, величина критической скорости охлаждения сложным образом зависит от внутренних параметров вещества (температура и теплота плавления, энергия и вязкость активации вязкого течения, поверхностного натяжения на границе жидкость-кристалл). Наряду с этим, к примеру, для селенидов мышьяка, громаднейшее влияние на величину критической скорости охлаждения оказывает температура плавления. Конкретно исходя из этого в совокупностях с эвтектическим характером сотрудничества компонентов составы с минимальной критической скоростью охлаждения близки к составам эвтектик.
Критическая скорость охлаждения может рассматриваться в качестве количественной меры стеклообразующей свойстве. Вправду, чем меньше критическая скорость охлаждения, тем более мягкими являются условия получения вещества в стеклообразном состоянии, тем легче возможно получено стекло.
С позиций кинетической теории стеклообразования для любого вещества возможно подобрать критическую скорость охлаждения, при которой оно возможно переведено в стеклообразное состояние без кристаллизации. Исходя из этого, строго говоря, вопрос о том, какие конкретно вещества смогут при охлаждении образовывать стекла, смысла не имеет. По большей части, существующие на данный счет ограничения связаны с большими размерами примера, что возможно взят в стеклообразном состоянии. Проиллюстрировать это возможно следующим образом.
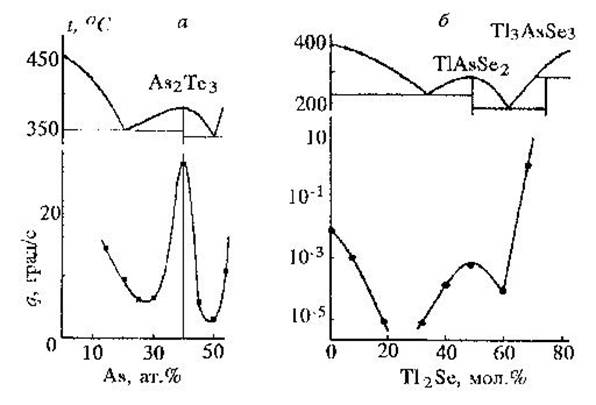
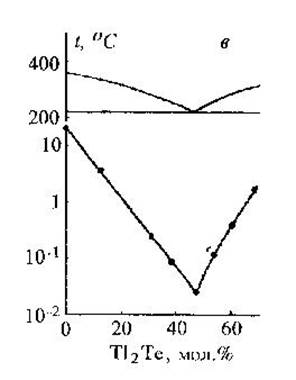
Рис.9. концентрационная диаграммы зависимость и фрагмент состояния критической скорости охлаждения в совокупностях As-Te (a), As2Se3-Tl2Se (б) As2Te3-Tl2Te (в).
Разглядим каплю жидкости радиуса r, которая находится при температуре плавления. Охлаждение центра капли с максимальной скоростью будет протекать в том случае, если каплю поместить в среду, безотносительная температура которой Т=0. Временная зависимость температуры в центре капли возможно отыскана из уравнения теплопроводности, представленного в следующем виде:
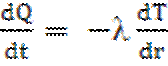либо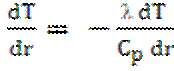
,
где ? – теплопроводность жидкости, Cp — теплоемкость жидкости, Q — количество теплоты. С учетом начальных условий (t=0, Т=Тпл), полагая, что , по окончании разделения переменных и интегрирования, возможно возьмёт приближенную зависимость температуры в центре капли от времени охлаждения
T = Тплexp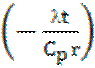 
.
Для получения стекла нужно переохладить жидкость до температуры стеклования Тg, которая в соответствии с эмпирической закономерности в большинстве случаев образовывает около 0.667 Тпл. Время охлаждения до данной температуры равняется
t = r Cpln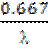 
.
Для идентификации примера нужно, дабы его толщина имела макроскопическую величину порядка 1 мкм. С учетом данной величины, и с учетом обычных значений теплоемкости (1 Дж . град-1 . см-3), теплопроводности неметаллических жидкостей (4 . 10-2 Дж . см-2 . с-1 . град-1) получается значение t ? 0.001 с. Для Тпл= 1000 К и Тg = 600 К это соответствует средней скорости охлаждения в 4 . 105 К/с. Данное значение скорости (с точностью до двух порядков) можно считать предельным значением скорости охлаждения, которая возможно достигнута чтобы получить вещество в стеклообразном состоянии. Следовательно, с макроскопической точки зрения граница между стеклообразующими и нестеклообразующими жидкостями находится вблизи критической скорости охлаждения порядка 107 К/с.
Так, при помощи понятия «критическая скорость охлаждения» современная теория кристаллизации жидкостей разрешает выяснить свойство любого вещества к стеклообразованию. Но для точных расчетов нужно знать такие свойства вещества, как температура и теплота плавления, а основное, параметры температурной зависимости вязкости переохлажденной жидкости. Конкретно последнее свойство фактически сводит на нет предсказательные возможности кинетической теории стеклообразования. Иначе, из этого направляться, что неприятность стеклообразования есть личной проблемой его свойств строения и взаимосвязи вещества.
Трудности применения кинетической теории к описанию процессов стеклообразования в конкретных совокупностях обусловливает существование бессчётных эмпирических параметров, связывающих возможность образования стекол в конкретных совокупностях с некоторыми особенностями этих совокупностей (такими, как электронная структура возможно стеклообразующих атомов, их координационное число, энергия и характер химического сотрудничества между ними, температура ликвидуса, тип и количество структурных элементов, вязкость и т.п.). Все эти трудности обусловливают частное использование аналогичных параметров, т.к. обычно преувеличивается значение каких-либо отдельных особенностей жидкости либо кристалла для процесса стеклообразования без какое количество-нибудь важного теоретического подтверждения со стороны кинетической теории стеклообразования. Однако, полуэмпирический подход для предсказания стеклообразования для совокупностей, информация о особенностях которых недостаточна для строгого применения кинетической теории, обычно не редкость нужным.
Структура кристаллических и стеклообразных тел.
На сегодня нет сомнений в том, что кристаллическое состояние вещества изучено намного лучше, несравненно больше и несравненно правильнее, чем стеклообразное. Исходя из этого при описании изюминок строения стекол целесообразно проводить аналогии с изюминками строения кристаллов. Во всех подряд случаях вещество в кристаллическом состоянии выстроено значительно несложнее, чем вещество в стеклообразном состоянии. И в любых ситуациях структурных изучений стекол прямо либо косвенно употребляются знания о строении кристаллов.
Главная изюминка строения кристаллов содержится в том, что некое число атомов (ионов либо молекул) образует элементарную ячейку. В совершенном случае, зная особенности строения данной ячейки и закон перемещения ее в пространстве (трансляции) возможно обрисовать строение всего кристалла в целом, каким бы громадным данный кристалл ни был. Такое пространственное повторение перемещения элементарной ячейки носит название дальний порядок. Следовательно, для описания совершенного кристалла нужно лишь выяснить, какие конкретно атомы и как распределены в элементарной ячейке. Но для этого требуется сверхсложный опыт и достаточно сложные расчеты. На данный момент допустимо узнать правильное положение атомов в элементарных ячейках, содержащих пара десятков, в противном случае и сотен атомов. Для решения данной задачи пользуются рентгеноструктурным анализом. На поворачивающийся кристалл падает узкий рентгеновский луч заданной длины волны, что рассеивается лишь в фиксированных направлениях со строго определенной интенсивностью. Да и то, и второе вытекает из известных условий Лауэ, связывающих между собой длину волны, направления рассеяния и параметры кристалла. Полученные так экспериментальные эти по направлению рассеяния лучей, их соотношения и интенсивности между этими интенсивностями, по окончании компьютерной обработки разрешают выстроить искомую структуру элементарной ячейки с точностью по положению атомов до десятитысячных долей ангстрема.
В случае, если исследуется несколько кристалл вещества, а поликристаллический пример, складывающийся из солидного числа весьма небольших кристалликов, непоследовательно ориентированных в пространстве, то первичный падающий луч будет рассеиваться, образуя конусы, вдетые приятель в приятеля. Определение их интенсивностей проводится по линии их центров, и итог изображается на картинках в виде вертикальных линий, высота которых пропорциональна интенсивности, а положение определяет угол рассеяния (рис.10).
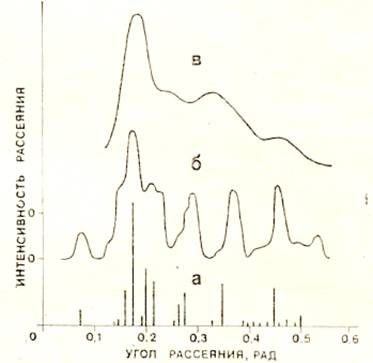
Рис.10. Рентгенограммы (дебаеграммы) метасиликата натрия в разных агрегатных состояниях: а – поликристалл, б – смесь небольших кристалликов, в – стекло.
Определение структуры элементарной ячейки по дебаеграмме допустимо лишь для несложных кристаллов (рис.10 а).
При изучения структуры настоящего кристалла, появляется дополнительный последовательность затруднений, которые связаны с наличием в его структуре разного рода недостатков (искажений решетки, вакуумов, включений, и т.п.), каковые приводят к дополнительному рассеянию лучей вне направлений, вытекающих из условий Лауэ. Наряду с этим появляется еще более непростая задача – выяснить эти недостатки время от времени по весьма не сильный и размытым рефлексам. К примеру, в поликристалле, складывающемся из весьма небольших кристалликов (менее 0.1 мкм), дебаевские линии на рентгенограмме будут расширяться (рис.10 б) и по их ширине возможно вычислить размеры этих кристалликов.
Использование рентгеноструктурного анализа для выяснения строения аморфных веществ и, например, стекол выясняется более сложным, если сравнивать с изучением строения кристаллов. Так как в какой-то степени стекло возможно представить как некое подобие кристалла (кристаллитом), в котором заметно искажена любая элементарная ячейка и где отсутствует дальний порядок. Неудивительно, что рентгенограммы стекол резко отличаются кроме того от рентгенограмм поликристаллов (рис.10 в): вместо четких линий появляются широкие размытые полосы, частично перекрывающие друг друга. Наряду с этим расчеты количества элементарных ячеек в аналогичной очень сильно искаженной кристаллоподобной структуре по ширине размытых полос приводят к отрицательному выводу: кристаллиты должны содержать 1 -2 элементарные очень сильно искаженные ячейки и тем самым теряется суть самого понятия «кристаллит».
Но к размытой рентгенограмме (рис.10 в) возможно доходить совсем в противном случае. Используя к кривой интенсивности (которая характеризует распределение интенсивности на протяжении любого радиального направления) строгую математическую обработку (анализ Фурье) возможно преобразовать кривую интенсивности в кривую радиального распределения в стекле ядерной плотности около любого, принятого за начальный, атома в стекле. Такая кривая для кварцевого стекла продемонстрирована на рис.11.
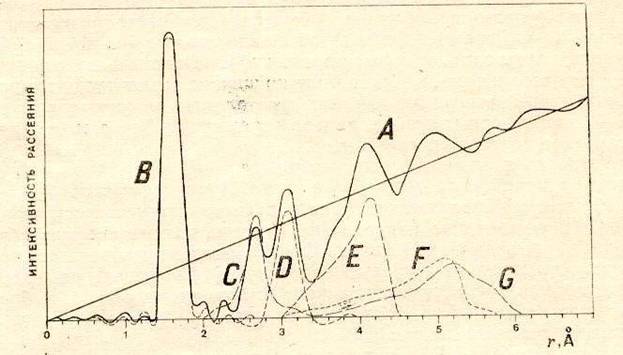
Рис.11. Кривая радиального распределения для кварцевого стекла.
А – измеренная кривая. Вычисленные из кривой А вклады от отдельных пар атомов: B (Si-O); C (O-O); D (Si-Si); E (Si-O-второй кислород); F (O-O-второй кислород); G (Si-Si-второй кремний); r – расстояние от центра атома, принятого за начальный.
Функция радиального распределения атомов, которая помогает для описания структуры аморфных и стеклообразных веществ, определяется следующим образом: произведение G(r)dr имеется число атомов, находящихся в шаровом слое от r до r+dr. Количество шарового слоя равен произведению площади поверхности 4?r2 на толщину слоя dr. Исходя из этого возможно записать следующее выражение
G(r)dr = 4??(r)r2dr,
где ?– плотность вещества в данной точке, выраженная как число частиц на единицу количества (? зависит от расстояния). Функция радиального распределения атомов обязана владеть следующими особенностями: шаровой симметрией, непрерывностью, независимостью от выбора центрального атома.
Функция радиального распределения атомов характеризует упорядоченность во обоюдном размещении атомов. К примеру, для совершенного газа характерно полное отсутствие какой-либо упорядоченности и его состояние характеризуется средней плотностью ?. Исходя из этого для совершенного газа функция G(r) является параболой . В случае, если функция G(r) характеризуется какими-либо изюминками в виде минимумов и максимумов, то это говорит о наличии некоторых преимущественных обоюдных ориентаций атомов относительно друг друга, т.е. о существовании некоей структуры.
Функция G(r) определяется из данных по рассеянию рентгеновских лучей под громадными углами. Для рассеяния электромагнитного излучения при прохождении его через вещество имеет значение степень однородности этого вещества. Рассеяние не происходит в том случае, в то время, когда характерный размер неоднородностей (центров рассеяния) d довольно много меньше длины волны падающего излучения d
Возвращаясь к рис.11, направляться подчернуть, что положение максимумов на данной кривой определяет (с точностью до 0.01A) самые вероятные расстояния между атомами, а по величине площади под максимумами возможно выяснить количество соседей около атома, выбранного за начальный, т.е. его координационное число. Так, анализ первого, самый отлично разрешенного максимума, говорит о том, что в кварцевом стекле любой атом кремния окружен четырьмя атомами кислорода в форме тетраэдра и данный тетраэдр, конечно, в самых разных пространственных положениях, воспроизводится по всему количеству стекла. Так, по первому максимуму кривой радиального распределения с высокой точностью возможно выяснить первую координационную сферу, ближайшее окружение атомов, т.е. ближний порядок.
Второй максимум на кривой радиального распределения относится к расстоянию между атомами кислорода в тетраэдра. Третий максимум, частично перекрывающийся со вторым, более размыт: он определяет расстояние между двумя атомами кремния в соседних тетраэдрах. Анализ первого и третьего максимумов разрешает установить факт несимметричного размещения двух атомов кремния около атома кислорода. Угол между связями кислорода с этими двумя атомами кремния выясняется не постоянным и изменяется в пределах от 130 до 160о при самоё вероятном значении, близком к 144о. Диаметр области ближнего порядка в стеклообразном оксиде кремния лежит в пределах 15 – 20 A, не смотря на то, что границы данной области размыты, и, следовательно, неизвестны. Однако, на основании кривой радиального распределения для этого стекла были вычислены не только расстояния в кремний-кислородного тетраэдра, но и еще пять самые вероятных межатомных расстояний в соседних тетраэдрах.
В современных изучениях, в связи с увеличением разрешающей свойстве применяемых устройств, выявляется пара большее число максимумов, чем это продемонстрировано на рис.2. Но и в этом случае выявляется не более 9 – 12 пиков на радиальном расстоянии 9 – 10 A. По мере удаления от центрального атома, эти пики размываются все больше и их разрешение (разделение) и идентификация (т.е. отнесение к расстояниям между конкретными атомами) делается затруднительным. В этом случае приходится прибегать к моделям, для которых определяется «модельная» кривая радиального распределения, которая и сравнивается с экспериментальной кривой; по окончании чего вводятся те либо иные поправки, улучшающие совпадение эксперимента и теории. направляться подчернуть, что подобный подход хоть и имеет под собой землю, но не имеет возможности претендовать на полную однозначность, т.к. в любой момент принципиально допустимо использование совсем хороших друг от друга моделей, приводящих к кривым радиального распределения, соответствующим экспериментальной.
Полученная экспериментально кривая радиального распределения есть объективной чёртом (собственного рода паспортом) ближнего порядка структуры стекла. Каждые структурные модели строения стекла, полученные с применением каких-либо структурно-чувствительных способов, не смогут принимать во внимание точными, в случае, если вычисленные по ним кривые радиального распределения не соответствуют экспериментальным.
Подобная трактовка рентгенограмм стекол абсолютно соответствует модельным представлениям Захариасена, в соответствии с которым атомы (либо ионы) стекла образуют постоянную неупорядоченную пространственную сетку. Проекция на плоскость аналогичной сетки стеклообразного оксида кремния представлена на рис.12 (б). Потому, что это двумерное изображение, любой атом кремния окружен только тремя атомами кислорода, четвертый атом кислорода на схеме отсутствует. Ясно, что в настоящем тетраэдре три (а в действительности четыре) атома кислорода и атом кремния не лежат в одной плоскости и представленная проекция дает искаженную картину. Однако, она верно отражает главные идеи трехмерной пространственной сетки стекла, и ввиду собственной наглядности взяла во всемирной стекольной литературе самое широкое распространение.
Рис.12. Схематическое изображение на плоскости строения кристаллического оксида кремния (а), стеклообразного оксида кремния (б) и натриевосиликатного стекла (в).
Как продемонстрировали бессчётные рентгеновские и нейтронографические изучения, модель неупорядоченной пространственной сетки абсолютно подтверждается в отношении структур однокомпонентных стекол (стеклообразных оксидов кремния, бора, германия и некоторых вторых). Структура этих стекол характеризуется лишь ближним порядком и, как при любых вторых тел, тепловыми флуктуациями плотности, т.е. позванными тепловыми колебаниями атомов локальными отклонениями плотности от средней по всему примеру.
направляться подчернуть, что тепловые флуктуации плотности рассеивают рентгеновские лучи под малыми углами с практически постоянной во всем промежутке углов интенсивностью. Данный уровень интенсивности соответствует уровню, что возможно оценить методом термодинамических расчетов. Ближний порядок (т.е. кривая радиального распределения), уровень тепловых колебаний плотности – это все сведения, каковые возможно взять о структуре однокомпонентных стекол. Эти характеристики изменяются с трансформацией температуры, давления, облучения стремительными нейтронами и т.п., но при помощи рентгеноструктурного анализа изменение этих структурных параметров возможно отслеживать с высокой точностью.
Структура стекол более сложного состава, к примеру, содержащих оксиды щелочных металлов, существенно усложняется. Изменяется ближний порядок, что накладывает отпечаток на кривые радиального распределения: появляются дополнительные пики, соответствующие расстояниям между новыми типами атомов. Наряду с этим многоэлектронные атомы дают более резкие пики. Все это вносит дополнительные трудности в описании ближнего порядка для того чтобы рода стеклообразных совокупностей.
Но уже давно были предложены разные методы выяснения природы некоторых пиков на кривых радиального распределения, взятых для сложных стекол. К ним относятся изоструктурное (т.е. без заметного нарушения структуры) замещение легких атомов на более тяжелые (или трансформацией состава стекла при синтезе, или при помощи ионного обмена), применение разной рассеивающей свойстве атомов для рентгеновских и нейтронных лучей, применение аномального рассеяния рентгеновских лучей определенной длины волны отдельными атомами примера.
Для уточнения положения атомов в многокомпонентных стеклах чаще вторых употребляется метод изоструктурных замещений. В качестве индикаторов в стекла вместо легких атомов щелочных металлов вводится более тяжелое многоэлектронное серебро. Наряду с этим, размытые перегибы на кривой преобразовываются в резкие максимумы и по их положению выясняется вероятным значительно правильнее определять расстояния не только в первой, но и в нескольких последующих координационных сферах.
направляться подчернуть, что в стеклах, содержащих два либо более компонентов, наровне с тепловыми флуктуациями плотности неизбежно появляются тепловые флуктуации состава либо тепловые флуктуации концентрации, в следствии чего стекло делается химически неоднородным. Для таких сложных стекол догадка неупорядоченной сетки Захариасена делается несостоятельной, т.к. в этом случае для описания их неспециализированной структуры слишком мало знать лишь ближний порядок; нужно выяснить их строение на расстояниях, существенно превышающих межатомные, т.е. за пределами кривой радиального распределения. Для этого исследуется субмикроскопическая структура стекла, т.е. не структурные образования в пределах 10A, а образования от десятков до нескольких сотен а также тысяч ангстрем. С целью этого используются новые способы структурного анализа – то есть способ рассеяния рентгеновских лучей под малыми углами (РМУ) и способ рассеяния под средними углами (РСУ).
В следствии применения всех вышеперечисленных способов структурного анализа, на данный момент сформулированы и приняты неспециализированные закономерности в размещении атомов, образующих стекло, т.е. практически выяснено понятие «структура стекла». В зависимости от размеров структурного элемента если сравнивать с размерами атома, возможно выяснить структуру ближнего порядка, макроструктуру среднего и структуру порядка.
Как указывалось выше, под структурой ближнего порядка в большинстве случаев знают координационное число около какого-либо центрального атома, длины связей, углы между связями в элементарном многограннике, т.е. ближний порядок в стекле обрисовывает степень химической упорядоченности в пределах первой координационной сферы любого атома в составе стекла.
Средний порядок обрисовывает структурные мотивы взаимного расположения и сочленения элементарных многогранников (цепи, ленты, трехмерные элементы, слои, кольца и т.д.), т.е. он несёт ответственность за наличие некоторых закономерностей в упаковке элементарных полиэдров.
И, наконец, повторяемость элементов, образующих средний порядок, в какой-то мере может определять макроструктуру стекла. направляться подчернуть, что подобная повторяемость возможно и неполной, к примеру, в неоднородных двухфазных стеклах.
Кривая радиального распределения для кварцевого стекла.
А – измеренная кривая. Вычисленные из кривой А вклады от отдельных пар атомов: B (Si-O); C (O-O); D (Si-Si); E (Si-O-второй кислород); F (O-O-второй кислород); G (Si-Si-второй кремний); r – расстояние от центра атома, принятого за начальный.