Самый легко кинематические характеристики перемещения определяются в ортонормированном базисе (единичные базовые векторы ортогональны). В большинстве случаев с этим базисом связывают декартову совокупность осей . Три числа , каковые определяют положение точки М довольно данной совокупности координат,- это проекции радиуса-вектора на координатные оси:
(25)
Координаты движущейся точки
(26)
в большинстве случаев полагают два раза дифференцируемыми по времени функциями. Сами уравнения (26) именуют уравнениями перемещения точки в декартовой координатной совокупности либо уравнениями траектории точки в параметрической форме. В случае, если удается исключить из этих уравнений время , то комбинации любых двух взятых соотношений задают траекторию перемещения точки очевидно.
Для траектории перемещения, расположенной в одной плоскости (ее в любой момент возможно совместить с плоскостью ), в (26) достаточно записать только первые два уравнения или взять .
Продифференцировав (25) по времени, вектор скорости возможно представить в форме:
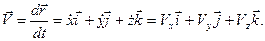(27)
где — проекции вектора скорости на соответствующие оси координат.
Модуль вектора скорости определяется по формуле
(28)
а направление этого вектора задается косинусами углов с соответствующими координатными осями («направляющие косинусы»):
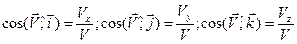. (29)
Сделав такую же последовательность операций, возможно взять выражения для вектора ускорения, его проекций, модуля и направляющих косинусов углов:
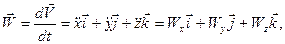
(30)
.
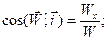
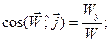
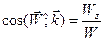ПРИМЕР 13. Морское орудие, дульный срез которого расположен на высоте над уровнем моря, создаёт выстрел под углом к горизонту; скорость вылета боеприпаса (см. рис.43).
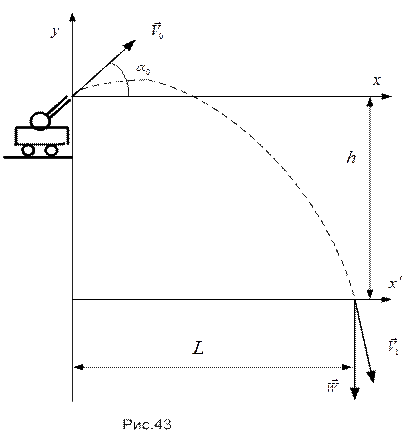
Полагая известными уравнения перемещения боеприпаса в декартовой координатной совокупности (начало координат на дульном срезе, — ускорение свободного падения, — время перемещения, сопротивление воздуха не учитывается):
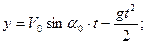
нужно вычислить дальность полета боеприпаса, его ускорение и скорость в момент удара о воду.
ОТВЕТ. Формулы для ускорения проекций и вычисления скорости на оси декартовой совокупности получаются дифференцированием по времени уравнений перемещения боеприпаса:
В общем случае значения размеров проекций смогут быть взяты лишь по окончании расчета времени полета боеприпаса . Увидим, что в разглядываемом случае на всем протяжении полета ускорение боеприпаса выяснилось постоянным и равным ускорению свободного падения.
Время полета боеприпаса определим из условия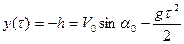 
.
Решив квадратное уравнение довольно , возьмём:
.
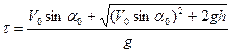Второй, отрицательный, корень уравнения отброшен, как не имеющий физического смысла.
Подставим определённое значение в формулы для проекций скорости:
Тогда величина скорости боеприпаса при ударе о воду будет
,
а дальность полета боеприпаса равна
.
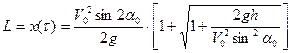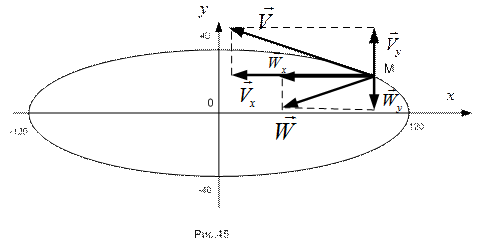
ПРИМЕР 14. Кривошип ОА кривошипно-шатунного механизма вращается с постоянной угловой скоростью . В начальный момент времени кривошип занимал горизонтальное положение. Протяженность шатуна АВ = ОА = 80 см. Точка М шатуна лежит на его середине. Составить уравнения для вычисления координат точек А, В и М механизма в декартовой координатной совокупности, изображенной на рисунке 44. Отыскать положение точки М в момент времени , конечно ускорения и проекции скорости, их модули и направляющие косинусы с координатными осями.
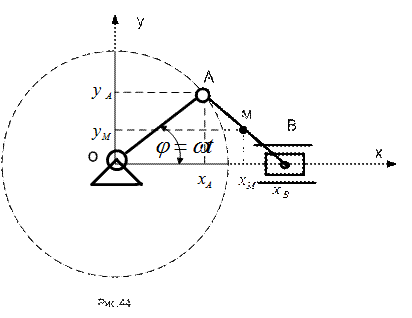
ОТВЕТ. Запишем выражения для проекций точек механизма на оси декартовой координатной совокупности:
.
Для нахождения положения точки М в заданный момент времени подставим значение в выражения для проекций, тогда
.
Для вычисления проекций скорости продифференцируем полученные выражения по времени и подставим величину . Тогда
.
Сейчас возможно вычислить модуль вектора скорости и его направляющие косинусы:
; 
.
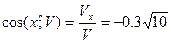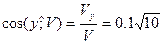Для вычисления проекций ускорения второй раз продифференцируем полученные выражения по времени и подставим величину . Тогда
.
Сейчас возможно вычислить модуль вектора ускорения и его направляющие косинусы:
; 
.
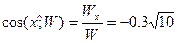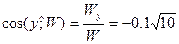Результаты выполненных расчетов нанесены на рисунок 45.
Кинематика несвободной точки (перемещение по заданной траектории)
Задание положения точки. Естественный трехгранник его оси и кривой
В технических приложениях выделяется круг задач о перемещении точки по заблаговременно известной траектории (в общем – криволинейной). В таких случаях для описания перемещения точки достаточно задаться только одной криволинейной координатой – длиной дуги , измеряемой на протяжении траектории от избранного на траектории начала (рис.46).
Перемещение точки определится законом трансформации дуги как функции времени
. (31)
Дуговая координата точки, в общем случае, отличается от пройденного пути, что есть неубывающей функцией времени (они совпадают при условии перемещения точки по траектории лишь в одну сторону).
Для ускорения и определения скорости несвободной точки напомним данные из дифференциальной геометрии пространственных кривых.
Плоскость , перпендикулярная касательной к траектории в точке , именуется обычной плоскостью (рис.47). Каждая прямая, лежащая в данной плоскости и проходящая через точку , направлена по нормали к кривой.
Касательную к траектории в точке , близко расположенной к точке , обозначим , а дугу (см. рис.46).
В случае, если перенести прямую параллельно самой себе в точку , то возможно совершить плоскость, содержащую прямые и ; угол между этими прямыми именуется углом смежности. С уменьшением до нуля эта плоскость, поворачиваясь около прямой , приближается к некоему предельному положению – соприкасающейся плоскости (см. рис.46). Прямая, по которой пересекаются обычная и соприкасающаяся плоскости, именуется основной нормалью к кривой в точке . Нормаль, перпендикулярная основной нормали, именуется бинормалью кривой. Плоскость , проходящая через бинормаль и касательную в точке М, именуется спрямляющей плоскостью.
Обычная, соприкасающаяся и спрямляющая плоскости образуют естественный трехгранник кривой в точке , а оси являются его осями. Единичные орты этих осей образуют ортонормированный базис локальной естественной координатной совокупности.
ускорение и Скорость точки
Отыщем проекции ускорения точки и векторов скорости в естественном базисе.
Радиус-вектор точки представляет собой сложную функцию времени , исходя из этого
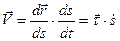. (32)
При выводе формулы учтено, что
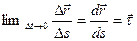— есть единичным ортом касательной к траектории перемещения точки .
По определению ускорения имеем
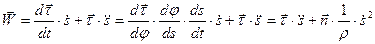. (33)
При выводе формулы учтено, что, во-первых,
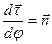— имеется орт основной нормали, а, во-вторых, кривизна траектории 
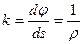, где — радиус кривизны траектории в точке .
Для доказательства первого события продифференцируем по углу смежности скалярное произведение
. Возьмём, что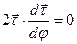 
, т.е. скалярное произведение двух векторов, расположенных в соприкасающейся плоскости, равняется нулю. Это допустимо лишь при их ортогональности.
Величина проекции ускорения на касательную
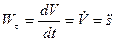именуется касательным ускорением, оно характеризует изменение вектора скорости по величине. Величина проекции ускорения на основную нормаль
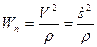именуется обычным ускорением, оно характеризует изменение вектора скорости по направлению. Обычное ускорение в любой момент направлено к центру кривизны траектории.
Полное ускорение точки равняется
.
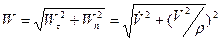Увидим, что в выбранной координатной совокупности отсутствуют проекции скорости на бинормаль и главную нормаль, конечно проекция на бинормаль ускорения точки.
Разглядим пара частных случаев перемещения точки.
1.Равномерное перемещение точки по прямой. Скорость перемещения не изменяется, исходя из этого равняется нулю касательное ускорение.
Обычное ускорение так же равняется нулю (вечно громадный радиус кривизны). Тогда
.
2.Равнопеременное перемещение по прямой ( ). Обычное ускорение равняется нулю. Тогда
; .
3. Равномерное перемещение по окружности радиуса . Вектор скорости направлен по касательной к окружности (к радиусу — под прямым углом). Скорость перемещения не изменяется по величине, исходя из этого равняется нулю касательное ускорение. Полное ускорение равняется обычному, т.е.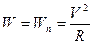 
. Ускорение направлено к центру окружности.
4. Равнопеременное перемещение по окружности радиуса . В этом случае скорость изменяется и по величине и по направлению, исходя из этого
; ; 
; 
.
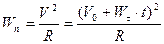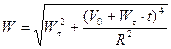ПРИМЕР 15. Центр тяжести катера, разгоняющегося из состояния спокойствия, обрисовывает дугу окружности радиуса R=75м. Его касательное ускорение изменяется по закону . Выяснить ускорение и скорость центра тяжести катера в момент, в то время, когда он пройдет путь 50 м.
ОТВЕТ. Интегрируя условие два раза по времени с учетом нулевых начальных условий, возьмём:
; .
Значение достигается в момент времени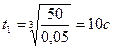 
. Наряду с этим скорость центра тяжести катера будет , а касательное ускорение — . Тогда полное ускорение равняется
.
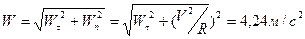5.4. Сообщение кинематических черт при разных методах задания положения точки
Как пример разберем переход от задания положения точки в декартовой координатной совокупности к ее заданию в естественной координатной совокупности, конечно выведем формулы связи между соответствующими кинематическими чертями.
Пускай заданы уравнения перемещения точки в декартовой координатной совокупности . Как уже говорилось выше, будем полагать эти функции два раза дифференцируемыми по времени.
Записанные уравнения смогут быть трактованы как уравнения траектории точки в параметрической форме. В случае, если удается исключить из этих уравнений время , то комбинации любых двух взятых соотношений задают траекторию перемещения точки очевидно как линию пересечения соответствующих поверхностей.
Для траектории перемещения, расположенной в одной плоскости (ее в любой момент возможно совместить с плоскостью ), достаточно записать первые два уравнения или взять .
Координаты точки начала перемещения получаются подстановкой начального времени (в большинстве случаев ) в уравнения перемещения, а анализ трансформации координат с ростом параметра определяет положительность либо отрицательность направления перемещения на протяжении траектории.
Сейчас возьмём зависимость криволинейной координаты от времени. Для этого воспользуемся формулами для вычисления скорости точки в декартовой и естественной координатных совокупностях:
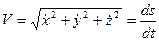(34)
Поделим переменные и заберём интегралы от правой и левой частей равенства. Возьмём
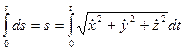(35)
ПРИМЕР 16. По заданным уравнениям перемещения точки на плоскости
;
отыскать ее траекторию, указать начало перемещения, его хорошее направление, конечно взять закон трансформации во времени криволинейной координаты точки.
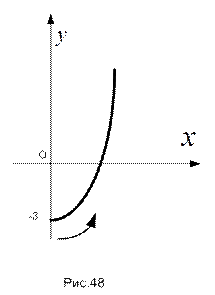
ОТВЕТ. Исключим время из уравнений перемещения точки, выразив время из первого уравнения и подставив его во второе уравнение. Возьмём уравнение параболы . Так как время не может быть отрицательным ( ), траектория точки – правая ветвь параболы (см. рис.48).
Подставив в уравнения перемещения, возьмём координаты точки начала перемещения:
; .
Анализ трансформации координат при возрастании времени говорит о том, что и ордината и абсцисса точки возрастают; что соответствует перемещению точки от начального положения вправо вверх (на рисунке хорошее направление перемещения указано стрелкой).
Для получения закона трансформации криволинейной координаты от времени сперва отыщем выражения для соответствующих проекций скорости ; , а после этого воспользуемся соотношением (2.4). Тогда
.
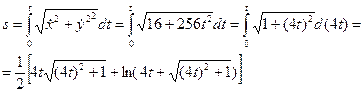ПРИМЕР 17. По заданным уравнениям перемещения точки на плоскости
;
отыскать ее траекторию, указать начало перемещения и его хорошее направление, конечно записать закон трансформации во времени криволинейной координаты точки.
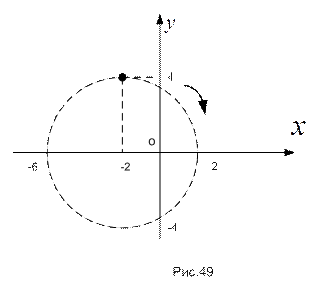
ОТВЕТ. Для исключения времени из уравнений перемещения воспользуемся известным тригонометрическим соотношением . В этом случае уравнение траектории будет иметь вид (окружность радиуса 4 см, перемещённая на 2 см на протяжении оси абсцисс влево, изображена на рис.49).
Подставив в уравнения перемещения, возьмём координаты точки начала перемещения:
; .
Анализ трансформации координат при возрастании времени говорит о том, что абсцисса точки возрастает, а ордината убывает; что соответствует перемещению точки от начального положения вправо вниз (на рисунке хорошее направление перемещения указано стрелкой).
Для получения закона трансформации криволинейной координаты от времени сперва отыщем выражения для соответствующих проекций скорости ; , а после этого воспользуемся соотношением (6.4). Тогда
.
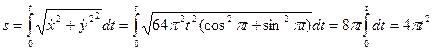Формула (2.4) показывает связь между вычислением скорости точки в декартовой и естественной координатных совокупностях
.
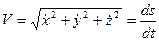Для получения связи между вычислением ускорения точки в указанных координатных совокупностях запишем формулы для его касательной и обычной составляющих ускорения через ускорения и проекции скорости на оси декартовой координатной совокупности:
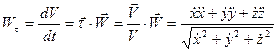(36)
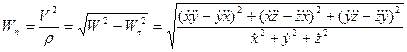
(37)
Радиус кривизны траектории в разглядываемой точке возможно вычислен как
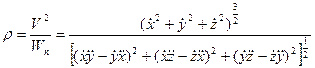(38)
ПРИМЕР 18. Продолжить ответ прошлого примера, выяснив положение точки М и вычислив в декартовой и естественной координатных совокупностях ее ускорение и скорость в момент времени .
ОТВЕТ. Для определения положения точки М подставим в уравнения перемещения точки:
; .
Сейчас вычислим ускорения точки и проекции скорости М в декартовой координатной совокупности, забрав соответствующие производные по времени от уравнений перемещения точки и подставив в них время . Тогда возьмём:
.
Все вычисленные характеристики нанесены на рис.50.
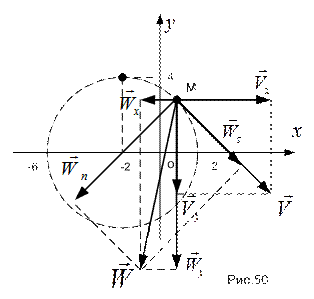
Для определения положения точки М на окружности подставим в закон трансформации криволинейной координаты:
.
Потому, что протяженность окружности радиуса будет , то точка М за указанное время прошла в хорошем направлении одну восьмую часть окружности.
Сейчас вычислим проекции и скорость ускорения точки на оси естественной координатной совокупности, забрав соответствующие производные от взятого выше закона трансформации криволинейной координаты :
.
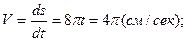
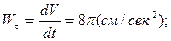
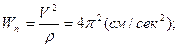
При жажде возможно убедиться, что вычисления по формулам (36, 37 и 38) совпадают с взятыми результатами.
Все вычисленные кинематические характеристики так же нанесены на рис.50.
ПРИМЕР 19. Продолжить ответ примера 16, выяснив положение точки М и вычислив в декартовой и естественной координатных совокупностях ее ускорение и скорость в момент времени .
ОТВЕТ. Для определения положения точки М в декартовой координатной совокупности подставим в уравнения перемещения точки:
; .
Сейчас вычислим ускорения точки и проекции скорости М, забрав соответствующие производные по времени от уравнений перемещения точки и подставив в них время . Тогда возьмём:
.
Для вычисления касательной и нормальной радиуса кривизны и проекций ускорения траектории в точке М воспользуемся формулами (36, 37 и 38). При перемещения точки по плоскости формулы примут более несложный вид:
;
;
.
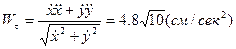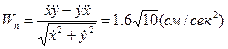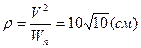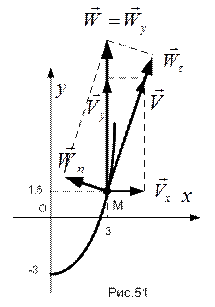
Все вычисленные характеристики нанесены на рис.51.
задачи и Вопросы для самоконтроля
1. Запишите формулы для ускорения и скорости точки при векторном методе задания ее положения. недостатки и Каковы достоинства этого метода?
2. В каком случае величины скорости и средней скорости точки сейчас времени совпадают?
3. Запишите формулы для ускорения точки и проекций скорости при задании ее положения в декартовой совокупности координат.
4. Вычислите величину скорости точки через 1 секунду по окончании начала перемещения, в случае, если ее положение на плоскости задано радиусом – вектором , где — орты координатных осей. Размерность проекций радиуса – вектора — метр, времени – секунда.
5. Что должно быть известно при естественном методе задания положения точки?
6. Что характеризует обычная составляющая ускорения? Запишите формулу для ее вычисления. Как направлена эта составляющая по отношению к траектории?
7. Что характеризует касательная составляющая ускорения? Запишите формулу для ее вычисления.
8. Как движется точка по траектории, в случае, если касательная и скорость составляющая ускорения сонаправлены? Если они направлены в различные стороны?
9. Чему равна проекция ускорения точки на бинормаль?
10. По какой траектории движется точка, в случае, если векторы ее ускорения и скорости сонаправлены?
Лекция 6: