Все числа мы привыкли записывать посредством десяти знаков-цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. К примеру, число, складывающееся из четырех сотен, четырех десятков и четырех единиц, мы записываем так: 444. Наряду с этим одинаковый символ «4» обозначает соответствующее число единиц, если он стоит на последнем месте, число десятков — в случае, если на предпоследнем, и число десятков десятков, т. е. сотен,— если он стоит на третьем месте от финиша. Таковой принцип записи чисел именуется позиционным либо п о-местным, в силу того, что любая цифра приобретает числовое значение не только в зависимости от собственного начертания, но и от того, на каком месте она стоит при записи числа. Позиционный принцип разрешает посредством десяти знаков-цифр записать любое сколь угодно много. Вправду, пускай нам дано целое число N. Чтобы записать его в отечественной совокупности, находим сперва остаток от деления N на 10, после этого остаток от деления частного на 10 и т. д. , пока в качестве частного не возьмём числа, меньшего десяти. К примеру:
N =523 = 10•52+3
52= 10•5 + 2
5 = 10•0 + 5
Полученные остатки и являются последовательными цифрами отечественного числа, записанного в позиционной десятичной совокупности-
N = 523,
либо, более детально,
N = 5•102 + 2•10 + 3.
Для тех, кто знаком с алгеброй, скажем, что каждое число М возможно представить в таком же виде.
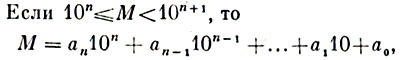
где любой из коэффициентов а0, а1, …, аn меньше 10 (это легко остатки от последовательного деления числа М на 10). Следовательно, любой из коэффициентов мы запишем посредством одной из отечественных десяти цифр. Следуя десятичному позиционному принципу, мы записываем число М так:
аnаn-1 … -а1а0,
где а0 свидетельствует число простых единиц, либо единиц первого разряда, содержащихся в М, а1 — число единиц второго разряда, т.е. десятков, а2 — число единиц третьего разряда, т. е. сотен, и т. д.
Число 10 именуется основанием отечественной совокупности.
Итак, для записи чисел мы пользуемся десятичной позиционной совокупностью счисления.