непрерывность и Пределы
Отметим кое-какие теоремы о пределах, каковые довольно часто используются для ответа задач.
В случае, если существуют конечные пределы 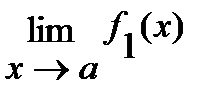 и
и 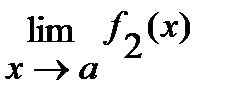 , то
, то
1) 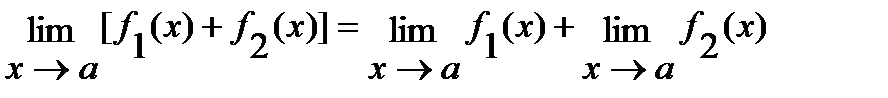 ;
;
2) 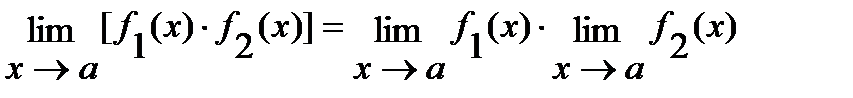 ;
;
3) 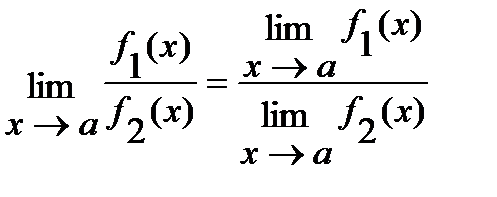 ( в случае, если
( в случае, если 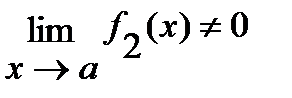 ).
).
Отметим еще два превосходных следствия и предела из них:
1) 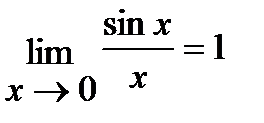 ;
;
2) 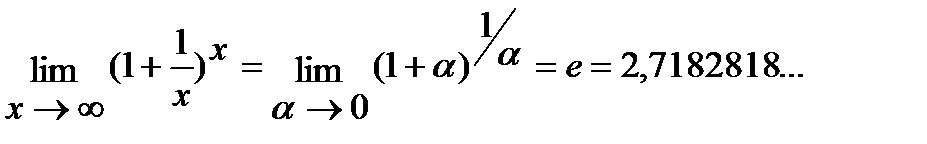 ;
;
3) 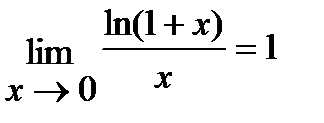 ; 4)
; 4) 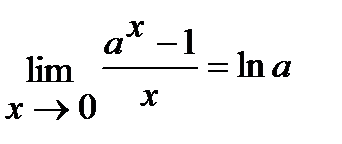 ; 5)
; 5) 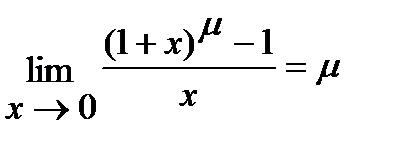 .
.
Задача. Отыскать указанные пределы, не пользуясь правилом Лопиталя:
а) 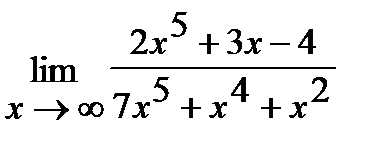 ;
;
б) 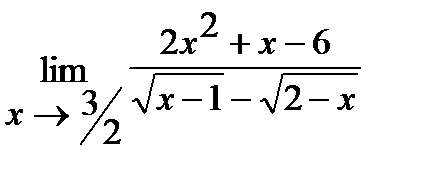 ;
;
в) 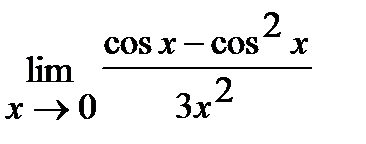 ;
;
г) 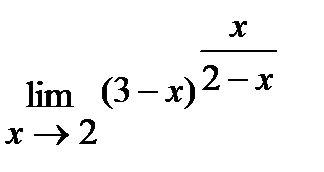 ;
;
д) 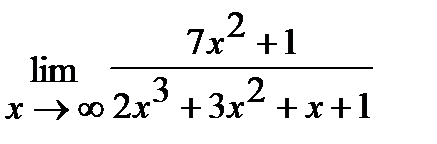 ;
;
е) 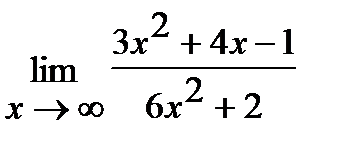 . ж)
. ж) 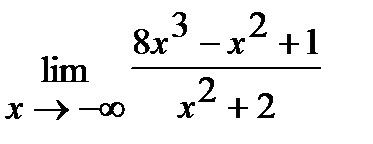 .
.
Ответ. а) В случае, если 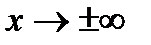 , то для нахождения предела частного двух многочленов достаточно поделить и числитель, и знаменатель дроби, стоящей под знаком предела, на
, то для нахождения предела частного двух многочленов достаточно поделить и числитель, и знаменатель дроби, стоящей под знаком предела, на 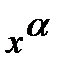 , где
, где 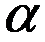 — степень многочлена, стоящего в знаменателе:
— степень многочлена, стоящего в знаменателе: 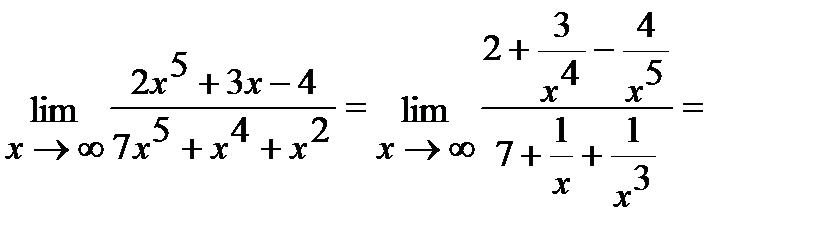
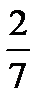 .
.
б) Умножим знаменатель и числитель дроби на 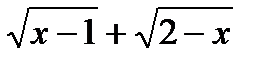 , избавившись тем самым от иррациональности в знаменателе. Итак,
, избавившись тем самым от иррациональности в знаменателе. Итак,
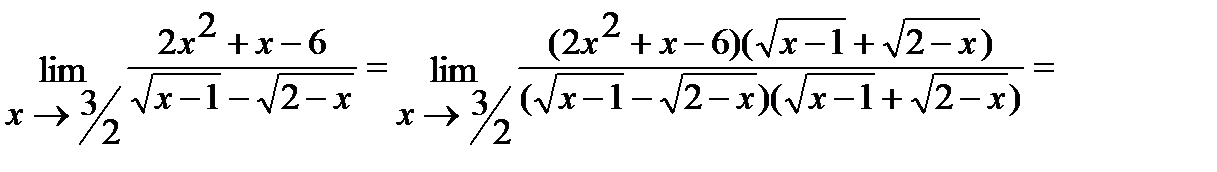
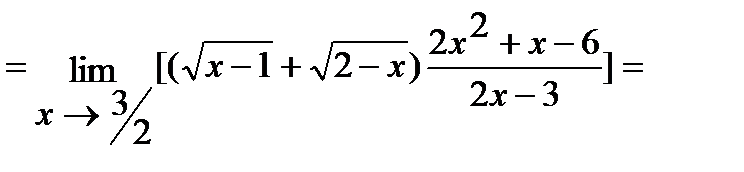
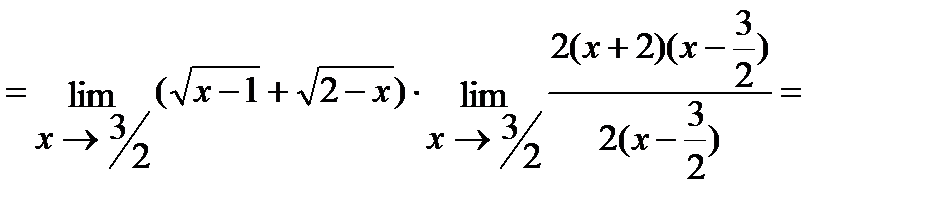
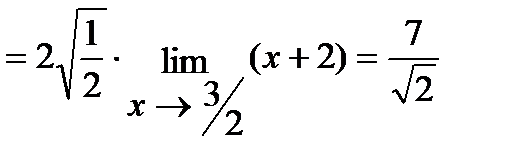 .
.
в) Для решения данной задачи воспользуемся первым превосходным пределом:
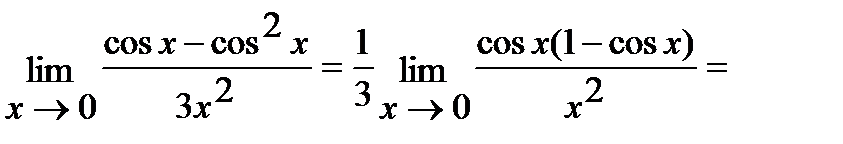
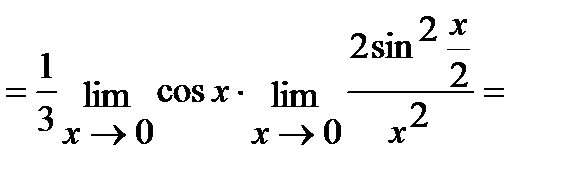
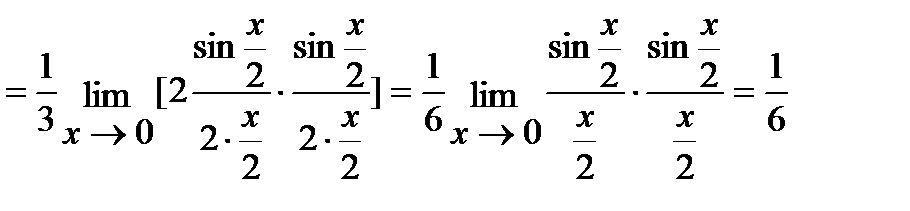
(Так как 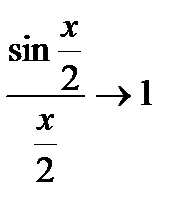 при
при 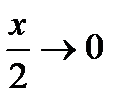 ).
).
г) Для решения данной задачи воспользуемся вторым превосходным пределом:
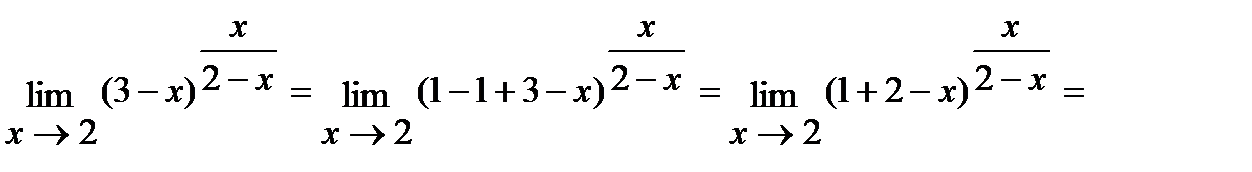
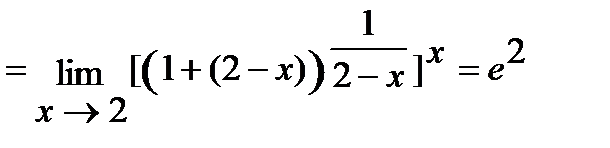 .
.
Последнее равенство вытекает из того, что в квадратной скобке стоит 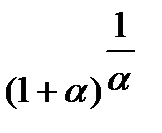 , где
, где 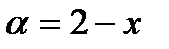 .
.
Решения задач е, ж подобны ответу задачи а.
К примеру, задача ж имеет следующее ответ:
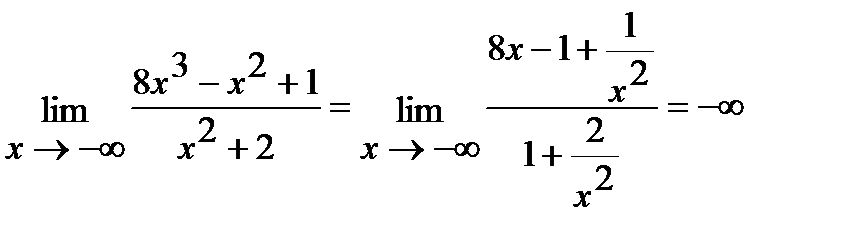 .
.
Производная функции
Производная функция 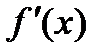 от функции
от функции 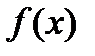 в данной точке
в данной точке 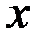 определяется равенством
определяется равенством
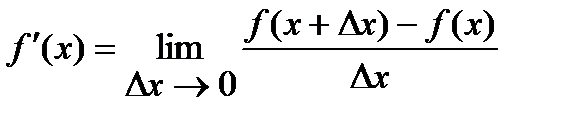 .
.
Таблица производных выглядит следующим образом:
1. 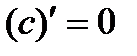 . 2.
. 2. 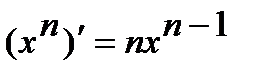 .
.
3. 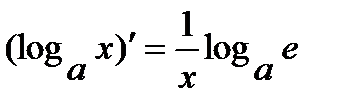 , в частности
, в частности 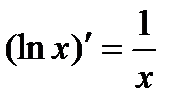 .
.
4. 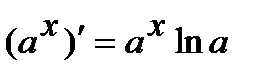 , в частности
, в частности 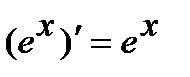 .
.
5. 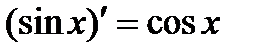 . 9.
. 9. 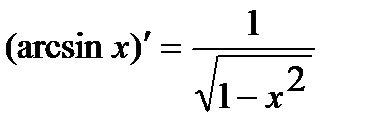 .
.
6. 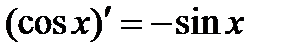 . 10.
. 10. 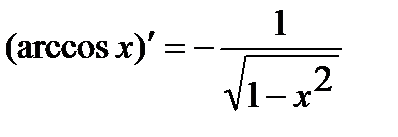 .
.
7. 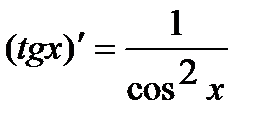 . 11.
. 11. 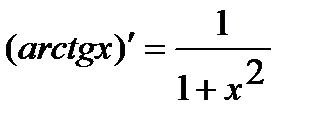 .
.
8. 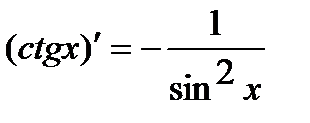 . 12.
. 12. 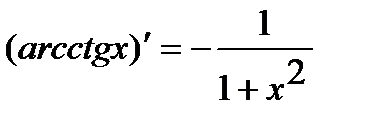 .
.
Главные правила дифференцирования
Задача. Отыскать производные следующих функций:
а) 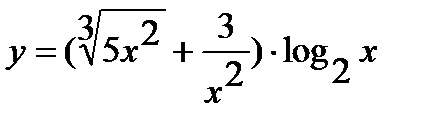 ; б)
; б) 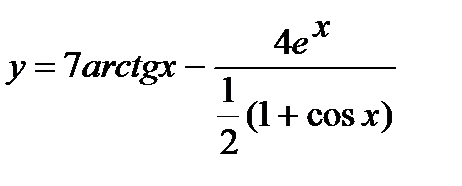 .
.
Ответ. а) Преобразуем выражение в скобках, переходя к дробным и отрицательным показателям. Возьмём
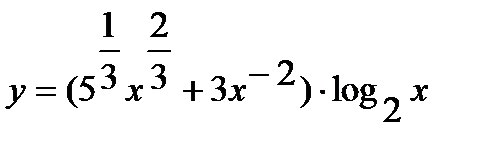 .
.
Применяя суммы дифференцирования и правило произведения находим 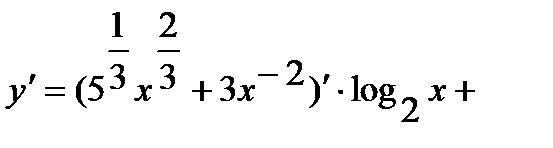
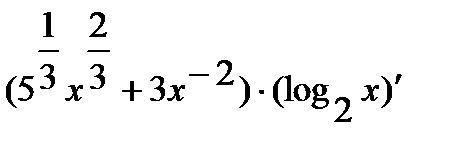 =
=
= 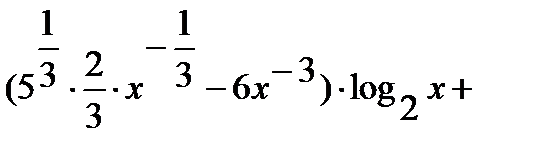
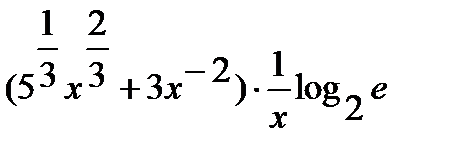 .
.
б) Совершим предварительное преобразование функции:
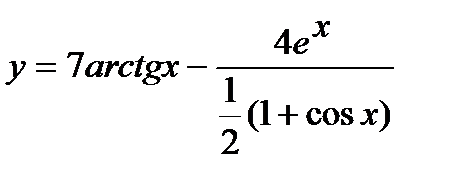 =
= 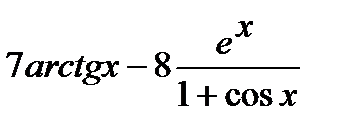 .
.
Применяя правила дифференцирования произведения, частного и суммы, возьмём
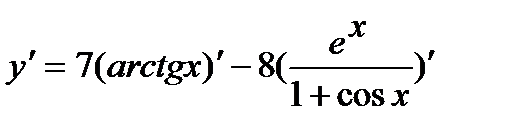 =
=
= 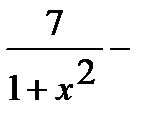
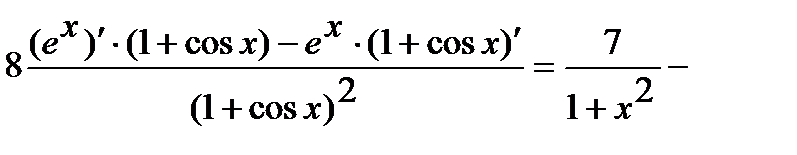
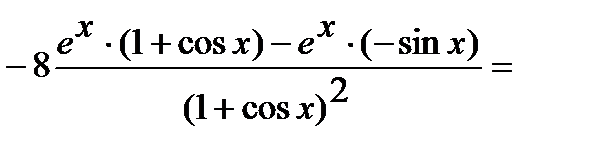
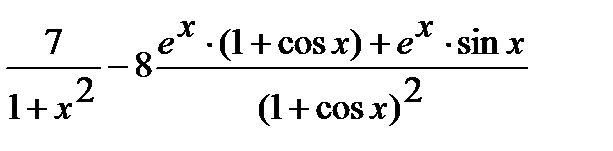 .
.
Дифференцирование сложной функции
В случае, если функция 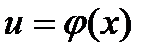 дифференцируема в точке
дифференцируема в точке 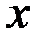 , а функция
, а функция 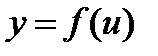 дифференцируема в точке
дифференцируема в точке 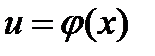 , то сложная функция
, то сложная функция 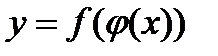 дифференцируема в точке
дифференцируема в точке 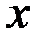 и
и
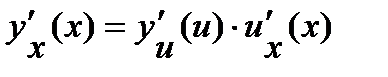 ,
,
где индекс внизу показывает, по какой переменной берется производная.
Задача. Отыскать производные следующих функций:
а) 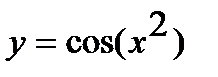 ; г)
; г) 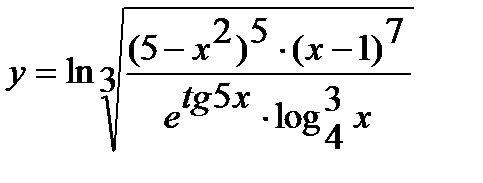 ;
;
б) 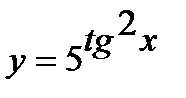 ;
;
в) 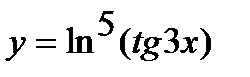 ;
;
Ответ. а) Функцию 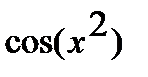 представим как композицию функций
представим как композицию функций 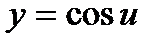 и
и 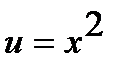 . Применяя таблицу производных, находим:
. Применяя таблицу производных, находим: 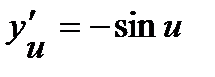 ,
, 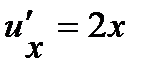 .
.
Тогда
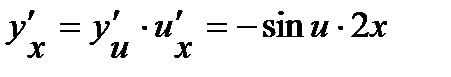
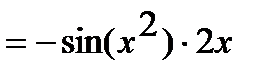 .
.
б) Функцию 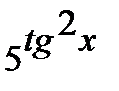 представим как композицию функций
представим как композицию функций 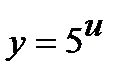 ,
,
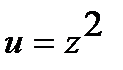 и
и 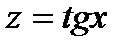 .Отыщем производные по промежуточным доводам:
.Отыщем производные по промежуточным доводам: 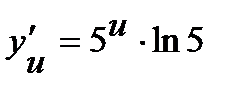 ,
, 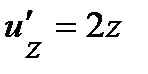 и
и 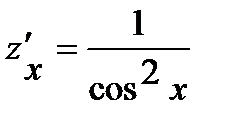 .
.
Производную сложной функции находим по формуле 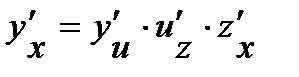 . Совсем возьмём
. Совсем возьмём 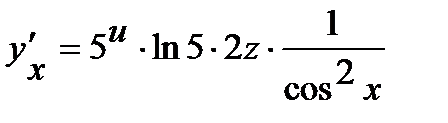 =
= 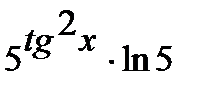
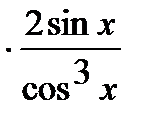 .
.
Подобно решается задача в:
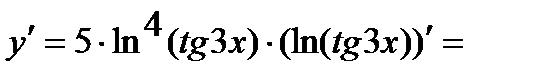
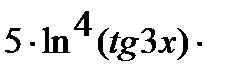
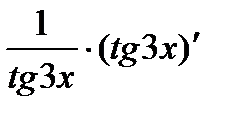 =
=
= 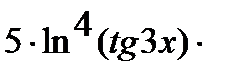
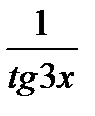
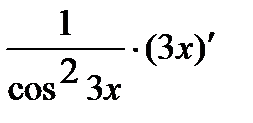 =
= 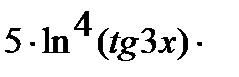
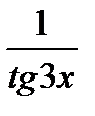
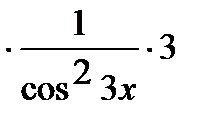 .
.
г) Предварительно упростив выражение, определяющее функцию, до вида
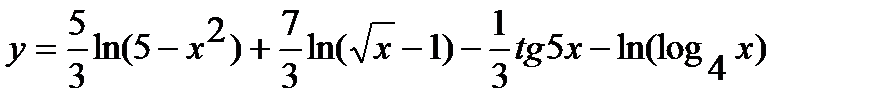 ,
,
находим производную:
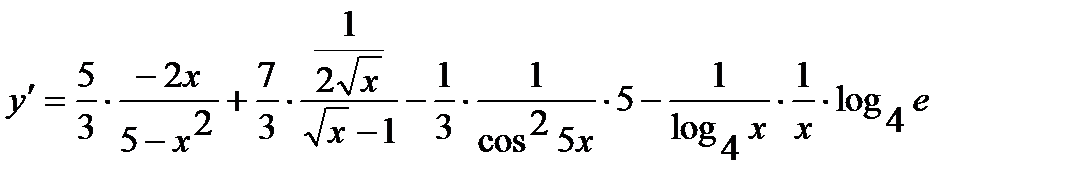 .
.
Методические указания к исполнению
Контрольной работы № 2
Приложение производной функции одной переменной
Теорема Лопиталя. Пускай функции 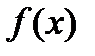 и
и 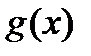 дифференцируемы в некоей окрестности точки
дифференцируемы в некоей окрестности точки 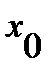 за исключением, возможно, самой точки
за исключением, возможно, самой точки 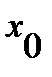 и постоянны в данной окрестности (включая саму точку
и постоянны в данной окрестности (включая саму точку 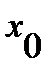 ), причем
), причем 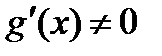 и
и 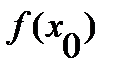 =
= 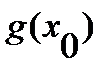 =0. Тогда, в случае, если существует
=0. Тогда, в случае, если существует 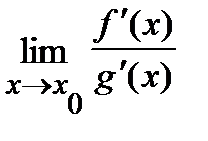 , то существует
, то существует 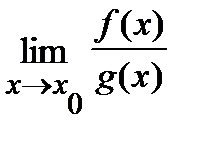 и эти пределы равны, другими словами
и эти пределы равны, другими словами
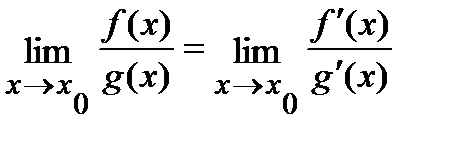 .
.
Так, для нахождения предела 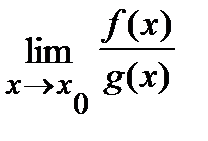 (для раскрытия неопределенности типа (
(для раскрытия неопределенности типа ( 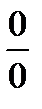 )) достаточно отыскать производные знаменателя и числителя дроби и вычислить предел
)) достаточно отыскать производные знаменателя и числителя дроби и вычислить предел 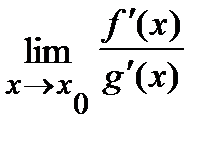 .
.
Такое же правило используется при 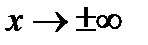 , и для раскрытия неопределенностей типа (
, и для раскрытия неопределенностей типа ( 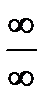 ).
).
Замечание. В случае, если производные знаменателя и числителя со своей стороны стремятся к нулю либо 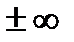 , то обрисованное правило используется повторно и без того потом.
, то обрисованное правило используется повторно и без того потом.
Пример.Вычислить 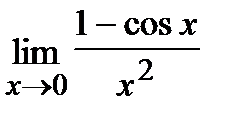 .
.
Ответ.
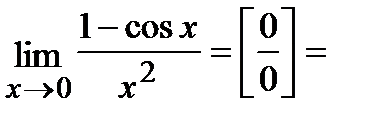
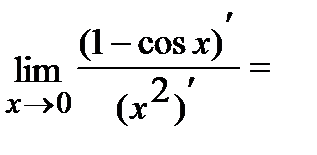
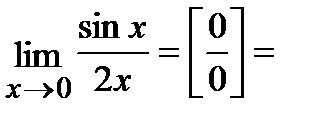
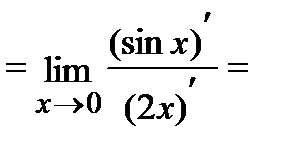
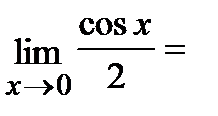
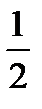 .
.
Пример.Вычислить 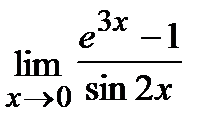 .
.
Ответ.
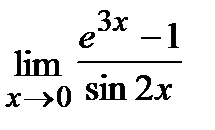 =
= 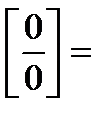
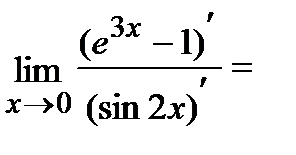
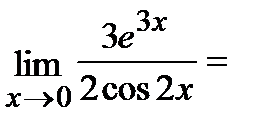
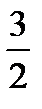 .
.
В случае, если функция 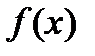 постоянна на замкнутом промежутке
постоянна на замкнутом промежутке 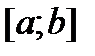 , то громаднейшее и мельчайшее значения она принимает либо на финишах этого отрезка, либо в точках ее экстремума. Следовательно, для ответа поставленной задачи нужно определить значения функции на финишах отрезка
, то громаднейшее и мельчайшее значения она принимает либо на финишах этого отрезка, либо в точках ее экстремума. Следовательно, для ответа поставленной задачи нужно определить значения функции на финишах отрезка 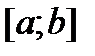 и в стационарных точках, которыми владел этому отрезку. После этого из них выбрать мельчайшее и громаднейшее значения.
и в стационарных точках, которыми владел этому отрезку. После этого из них выбрать мельчайшее и громаднейшее значения.
Пример.
Отыскать громаднейшее и мельчайшее значения функции 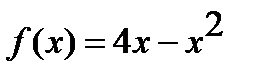 на отрезке
на отрезке 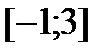 .
.
Ответ. Определяем критические, либо стационарные, точки функции 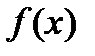 :
:
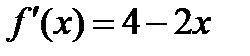 ;
; 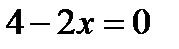 ;
; 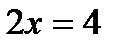 ;
; 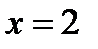 .
.
Разглядываем лишь те стационарные точки, каковые принадлежат отрезку 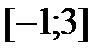 . Таковой точкой есть точка
. Таковой точкой есть точка 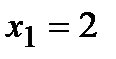 .
.
Вычисляем значения функции на финишах промежутка и в точке 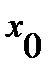 :
:
1) 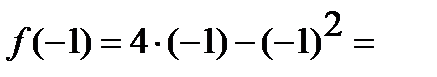
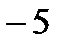 ;
;
2) 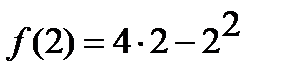 =
=  ;
;
3) 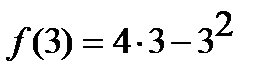 =
= 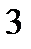 .
.
Ясно, что громаднейшее значение функции будет равняется  , которое она принимает в точке
, которое она принимает в точке 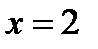 ; мельчайшее значение принимается функцией в точке
; мельчайшее значение принимается функцией в точке 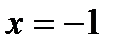 и равняется
и равняется 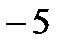 .
.
построение и Общее исследование функций их графиков комфортно делать по следующей схеме:
1) Отыскать область определения функции.
2) Отыскать точки пересечения с осями координат.
3) Узнать, не есть ли функция четной либо нечетной, периодической либо непериодической.
4) Отыскать точки экстремума функции, вычислить значения функции в этих точках. Установить промежутки монотонности функции.
5) Отыскать точки перегиба графика функции, вычислить значения функции в этих точках. Установить вогнутости графика и интервалы выпуклости функции.
6) Отыскать асимптоты графика функции.
7) Применяя данные исследований, выстроить график функции.
Пример. Изучить функцию 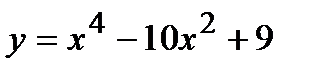 и выстроить ее график.
и выстроить ее график.
Ответ.
1) Функция выяснена и постоянна на всей оси. Итак, 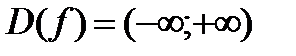 .
.
2) Отыщем точки пересечения с осями координат.
а) с осью ОХ: 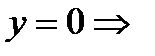
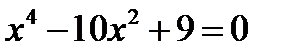
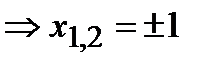 ,
, 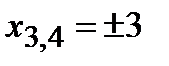 .
.
Следовательно, точки пересечения с осью ОХ — 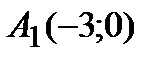 ,
, 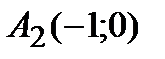 ,
, 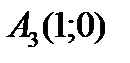 ,
, 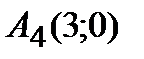 ;
;
б) с осью ОY: 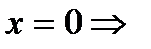
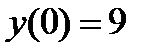 .
.
Следовательно, точка пересечения с осью ОY — 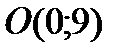 .
.
3) Функция четная, поскольку 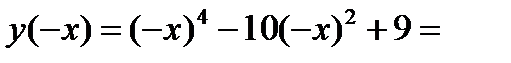
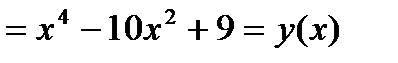 (исходя из этого ее график будет симметричен относительно оси OY).
(исходя из этого ее график будет симметричен относительно оси OY).
Функция непериодическая.
4) Посредством первой производной отыщем убывания функции и промежутки возрастания.
Имеем 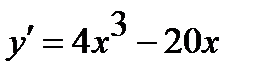 =0. Следовательно, точки
=0. Следовательно, точки 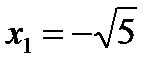 ,
, 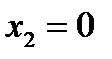 ,
, 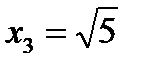 будут странными на экстремум. Разбиваем всю область определения на промежутки
будут странными на экстремум. Разбиваем всю область определения на промежутки 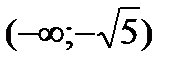 ,
, 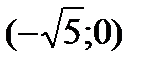 ,
, 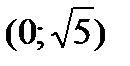 ,
, 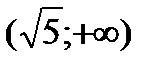 и исследуем функцию для
и исследуем функцию для 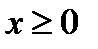 . Информация о поведении функции на промежутке
. Информация о поведении функции на промежутке 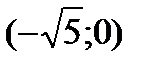 нужна для анализа функции в точке
нужна для анализа функции в точке 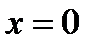 . По символу производной определяем монотонность функции на каждом промежутке. Данные исследований заносим в таблицу:
. По символу производной определяем монотонность функции на каждом промежутке. Данные исследований заносим в таблицу:
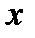
|
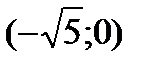
|
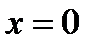
|
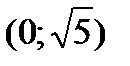
|
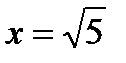
|
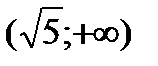
|
|
|
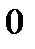
|
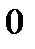
|
|
|
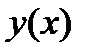
|
Возрастает | 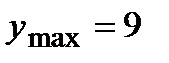
|
Убывает | 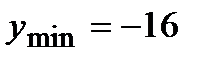
|
Возрастает |
5) Дабы изучить функцию на выпуклость, отыщем вторую производную: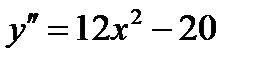 .Находим точки, в которых
.Находим точки, в которых 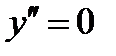 либо
либо 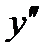 не существует.
не существует.
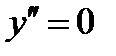 при
при 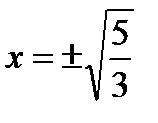 .
.
Исследуем символ второй производной на промежутках 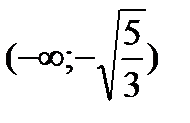 ,
, 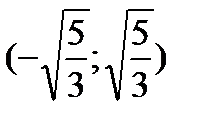 ,
, 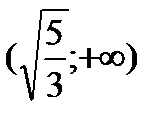 и данные исследований представим в таблице:
и данные исследований представим в таблице:
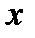
|
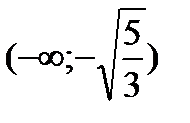
|
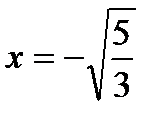
|
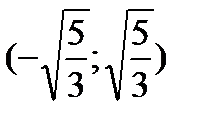
|
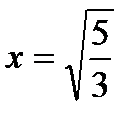
|
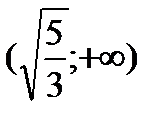
|
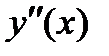
|
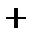
|
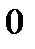
|
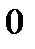
|
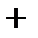
|
|
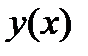
|
Выпукла | Перегиб | Вогнута | Перегиб | Выпукла |
6) Вертикальных асимптот нет, потому, что область определения функции – вся числовая ось.
Отыщем наклонную асимптоту 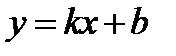 :
:
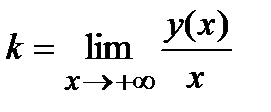 =
= 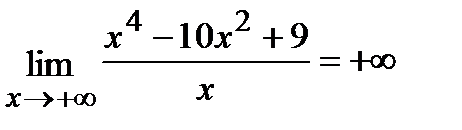 .
.
Следовательно, наклонных асимптот нет.
7) На базе исследования функции строим ее график (рис.1).
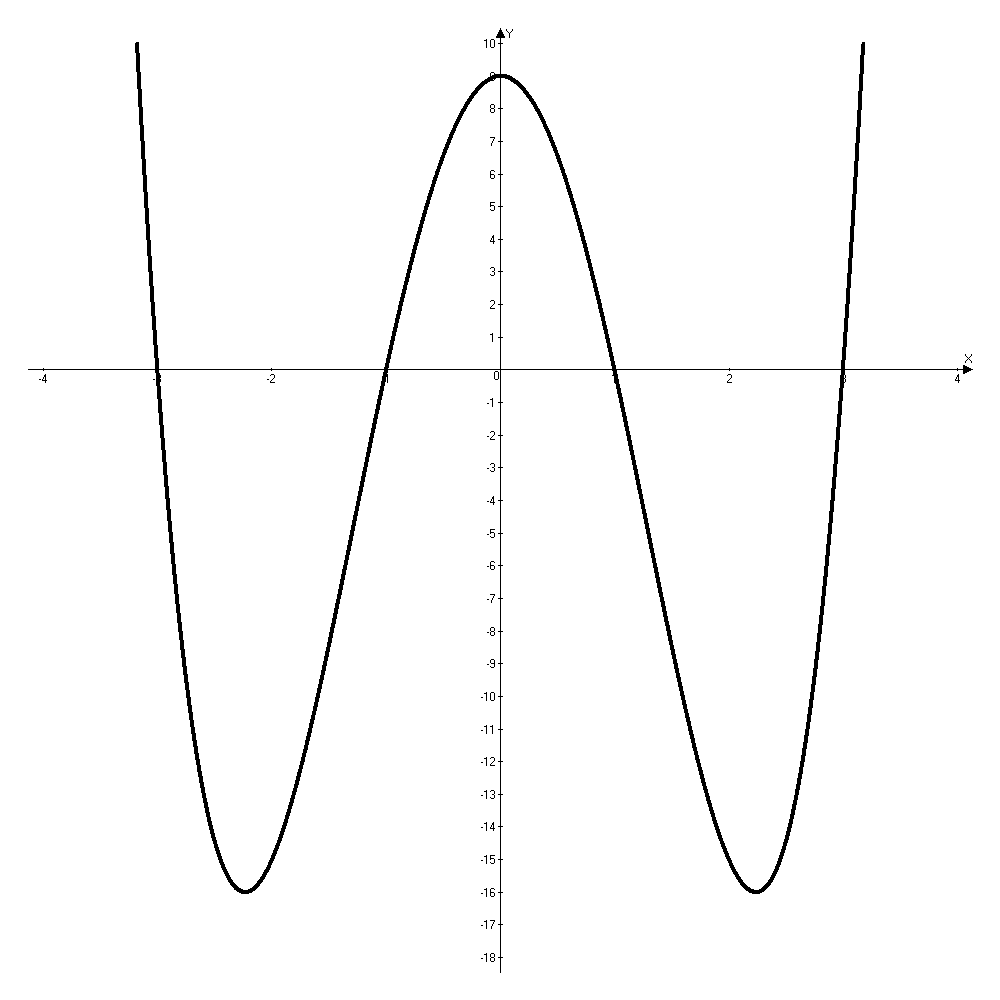
Рис. 1
Пример. Изучить функцию 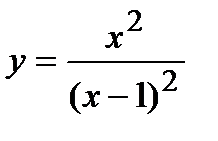 и выстроить ее график.
и выстроить ее график.
Ответ.
1) Функция выяснена и постоянна на всей оси, не считая точки 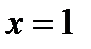 . Итак,
. Итак, 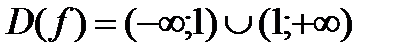 .
.
2) Отыщем точки пересечения с осями координат.
а) с осью ОХ: 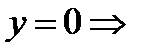
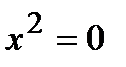
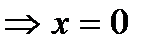 .
.
Следовательно, точка пересечения с осью ОХ — 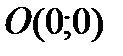 .
.
б) с осью ОY: 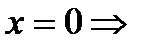
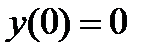 .
.
Следовательно, точка пересечения с осью ОY — 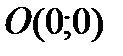 .
.
3) Функция неспециализированного вида, поскольку 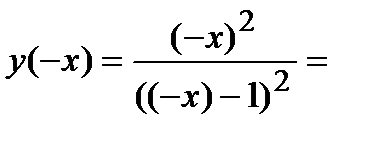
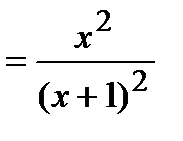 .
.
Функция непериодическая.
4) Посредством первой производной отыщем убывания функции и промежутки возрастания.
Имеем 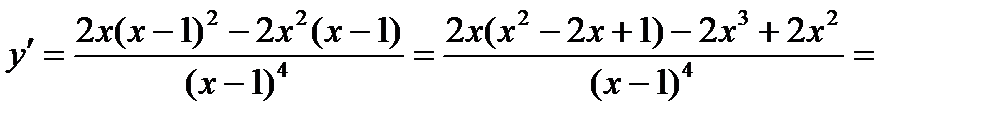
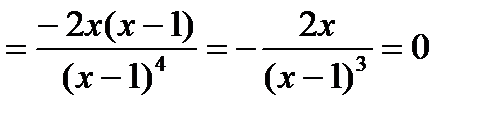 .
.
Следовательно, точка 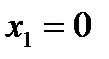 будет странной на экстремум. Точка
будет странной на экстремум. Точка 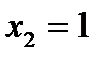 , в которой производная не существует, но в данной точке не существует и функция. Разбиваем всю область определения на промежутки
, в которой производная не существует, но в данной точке не существует и функция. Разбиваем всю область определения на промежутки 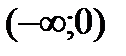 ,
, 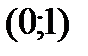 ,
, 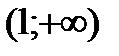 и исследуем функцию на указанных промежутках. По символу производной определяем монотонность функции на каждом промежутке. Данные исследований заносим в таблицу:
и исследуем функцию на указанных промежутках. По символу производной определяем монотонность функции на каждом промежутке. Данные исследований заносим в таблицу:
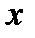
|
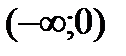
|
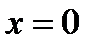
|
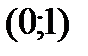
|
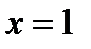
|
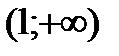
|
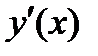
|
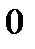
|
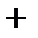
|
нет | ||
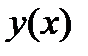
|
Убывает | 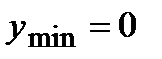
|
Возрастает | нет | Убывает |
5) Дабы изучить функцию на выпуклость, отыщем вторую производную:
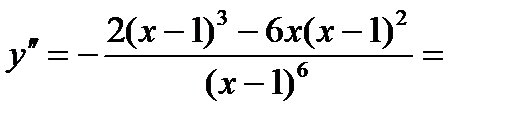
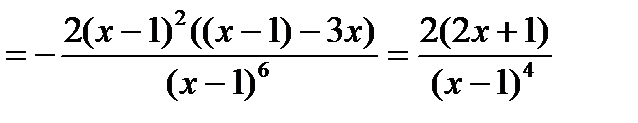 .
.
Находим точки, в которых 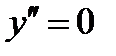 либо
либо 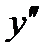 не существует:
не существует: 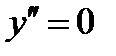 при
при 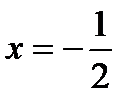 , не существует при
, не существует при 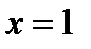 .Исследуем символ второй производной на промежутках
.Исследуем символ второй производной на промежутках 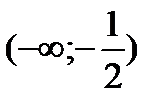 ,
, 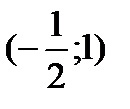 ,
, 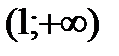 и данные исследований представим в таблице:
и данные исследований представим в таблице:
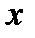
|
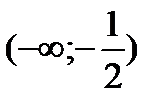
|
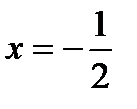
|
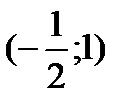
|
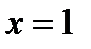
|
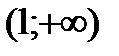
|
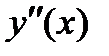
|
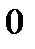
|
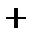
|
нет | 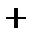
|
|
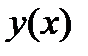
|
Вогнута | Перегиб | Выпукла | нет | Выпукла |
6) Отыщем вертикальные асимптоты:
Исследуем поведение функции в окрестности точки 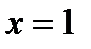 :
:
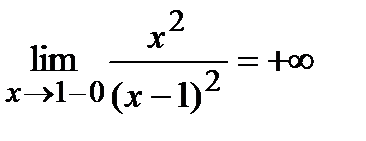 ;
; 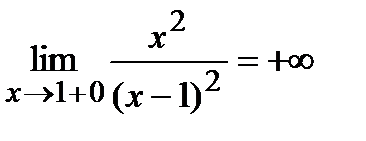 .
.
Пределы не конечны, следовательно, вертикальная асимптота имеет форму: 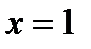 .
.
Отыщем наклонную асимптоту 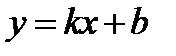 :
:
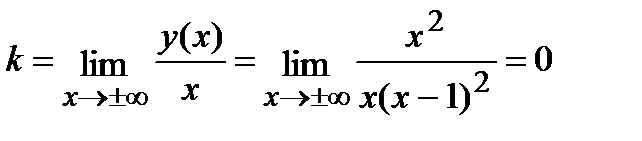 ;
;
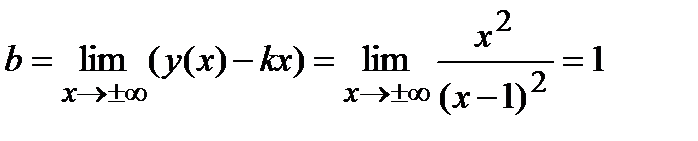 .
.
Следовательно, наклонная асимптота: 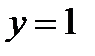 .
.
7) На базе исследования функции строим ее график (рис.2).
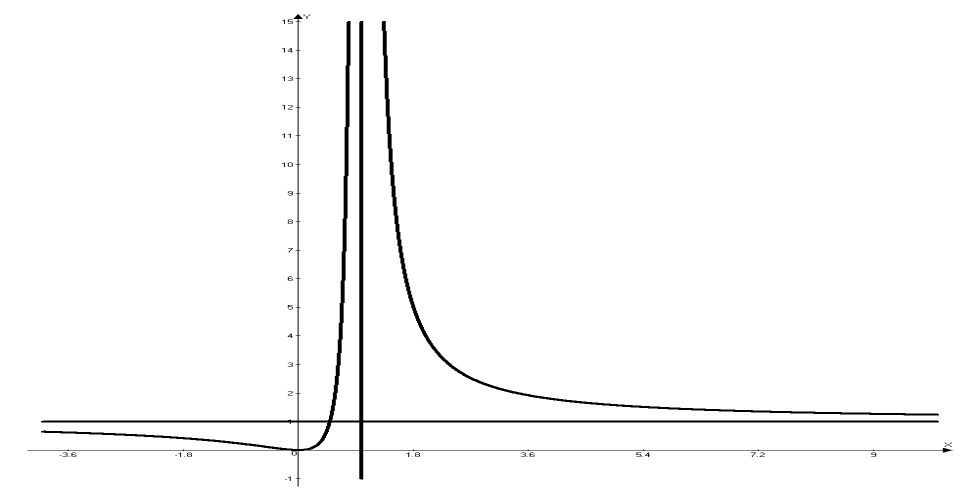
Рис. 2
Неизвестный интеграл
Функция 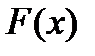 именуется первообразной функции
именуется первообразной функции 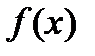 на некоем промежутке
на некоем промежутке 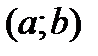 , в случае, если
, в случае, если 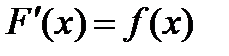 для всех значений
для всех значений 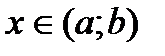 . В случае, если
. В случае, если 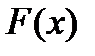 — первообразная
— первообразная 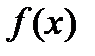 , то разумеется, что нескончаемое множество всех первообразных
, то разумеется, что нескончаемое множество всех первообразных 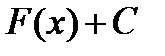 , отличающихся лишь константой, кроме этого будет первообразной
, отличающихся лишь константой, кроме этого будет первообразной 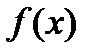 . Множество всех первообразных функций
. Множество всех первообразных функций 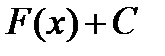
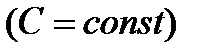 именуется неизвестным интегралом от функции
именуется неизвестным интегралом от функции 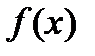 и обозначается
и обозначается 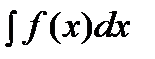 . Наряду с этим
. Наряду с этим 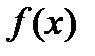 именуется подынтегральной функцией,
именуется подынтегральной функцией, 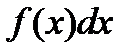 — подынтегральным выражением,
— подынтегральным выражением, 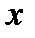 — переменной интегрирования.
— переменной интегрирования.
В соответствии с приведенному выше:
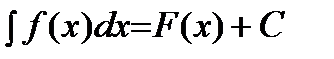 ,
,
где 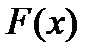 — некая первообразная функции
— некая первообразная функции 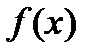 ;
; 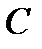 — произвольная постоянная.
— произвольная постоянная.
Неизвестный интеграл владеет следующими особенностями:
1) 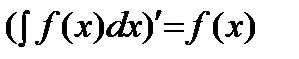 .
.
2) 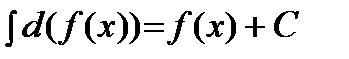 .
.
3) 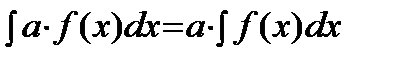 , где
, где 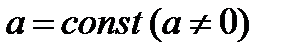 .
.
4) 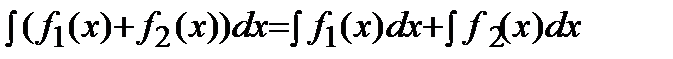 .
.
5) 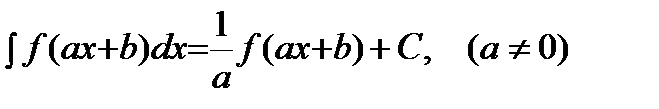 .
.
Таблица главных неизвестных интегралов:
1) 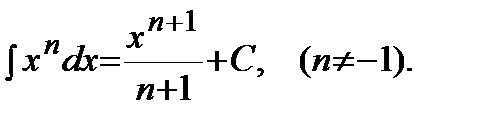
|
2) 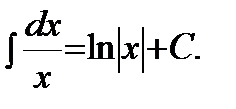
|
3) 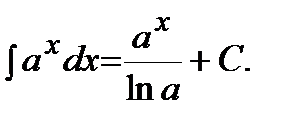
|
4) 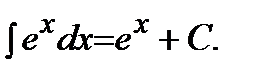
|
5) 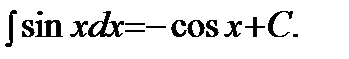
|
6) 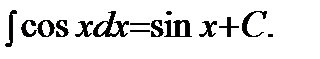
|
7) 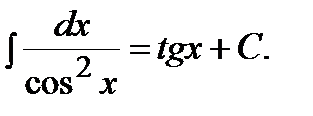
|
 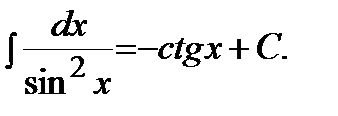
|
9) 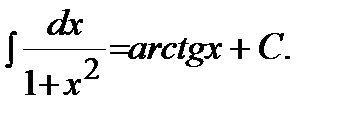
|
10) 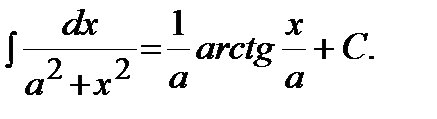
|
11) 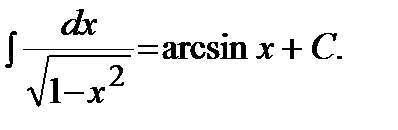
|
12) 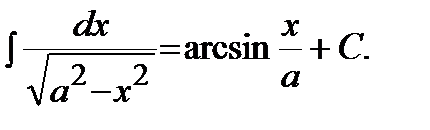
|
13) 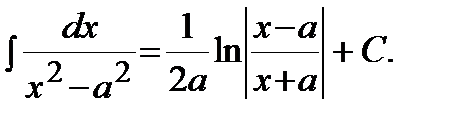
|
14) 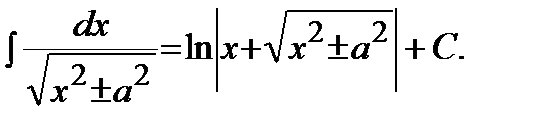
|
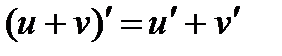 2.
2. 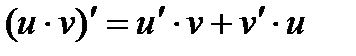 ,в частности,
,в частности,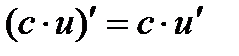 3.
3. 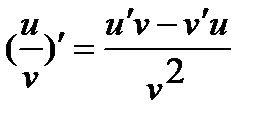 ,где
,где