УНИВЕРСИТЕТ ЭКОНОМИКИ, УПРАВЛЕНИЯ И ПРАВА (г.Казань)
Электронный учебник по инженерной графике
для независимой работы студентов
Составитель:
К.т.н., доцент Мутрискова М.А.
Казань – 2010
СПОСОБ ПРОЕКЦИЙ. ПРОЕКЦИИ ТОЧКИ
ЦЕНТРАЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ
Способ, которым в начертательной геометрии приобретают изображения, именуется способом проекций.
Проецирование содержится в проведении через каждую точку А, В, С, … изображаемого объекта и выбранный в некотором роде центр проекций S прямой линии (луча), именуемой проецирующей (линия. 1). Пересечение данной прямой с некоей плоскостью проекций я дает точку, являющуюся проекцией данной точки. На плоскости проекций наряду с этим каждой точке А, В, С. … предмета будет соответствовать лишь одна точка – проекция А’, В’, С’…*. Совокупность всех точек –проекций даст изображение (проекцию) данного предмета на плоскости я, т. е. на плоскости чертежа. Это изображение именуют центральной проекцией предмета.
Проецирование возможно создавать параллельными прямыми. Зададим плоскость проекций л и какое-либо направление s (линия. 2). Совершим через эти точки А, В, С,… проецирующие прямые линии, параллельные направлению s, и отыщем точки пересечения прямых с плоскостью л – проекции А’, В’, С’, … данных точек. Их именуют параллельными проекциями точек Л, В, С, … Можно считать, что параллельные проекции взяты проецированием из вечно удаленной точки 5 пространства, находящейся в направлении s, исходя из этого параллельное проецирование разглядывают как частный случай центрального.
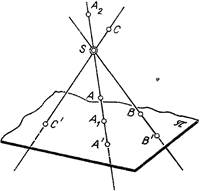
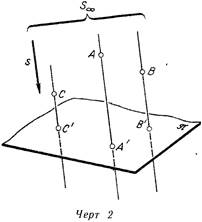
Линия. 1
* Центр проекций S не должен лежать в плоскости я В другом случае положение проекции точек плоскости я станет неизвестным, а проекции всех остальных точек пространства совпадет с точкой 5
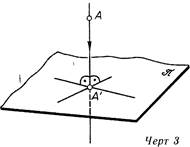
В случае, если направление проецирования перпендикулярно к плоскости л, то приобретаемые наряду с этим проекции именуют ортогональными либо прямоугольными (линия.3).
Центральное проецирование при определенных условиях дает наглядные изображения, подобные тем, каковые получаются на сетчатке людской глаза в ходе зрительного восприятия предметов. Но на них тяжело создавать измерения, сравнивать их. Используются такие проекции для изображения форм довольно громадных размеров в строительстве и архитектуре, где от чертежа особенно принципиально важно взять чувство, подобное зрительному.
Кое-какие виды параллельных проекций и первым делом ортогональные владеют достаточной наглядностью при изображении предметов довольно маленьких размеров (автомобилей и их подробностей) и позволяют легко создавать на них измерения. Это делает их незаменимыми при построении технических чертежей. Изучению свойств и законов построения конкретно этих Проекций посвящены последующие разделы книги.
ОБРАТИМОСТЬ ЧЕРТЕЖА. ОБРАЗОВАНИЕ ЭПЮРА
Чертеж, в особенности технический, должен быть обратимым, т. е. обязан давать возможность выяснить положение любой точки предмета или относительно плоскости проекций, или довольно второй данной точки. Это значит, что любая точка, заданная на изображении, обязана определять единственную точку изображенного объекта.
В случае, если обратиться к линия. 1 либо 2, то легко видеть, что проекция А’ может рассматриваться не только как проекции точки А, но и как проекция точек А\, Ai и т. д., лежащих на проецирующей прямой А-А’. Исходя из этого полученное изображение на данный момент не может нас удовлетворить.
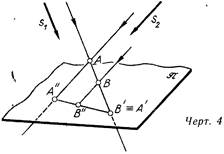
Зададим плоскость проекции л и два направления проецирования s\ и S2 (линия 4). Точка А будет иметь две проекции: А’ по направлению si и А по направлению S2. Вторая точка В, расположенная на проецирующем луче А-А’, по направлению si спроецируется точкой В’, совпадающей с точкой А’, но по направлению sz она спроецируется точкой В, хорошей от точки А. Сейчас по чертежу мы имеем
возможность заявить, что на нем нарисовано две точки — А и В; помимо этого, наличие двух проекций каждой из них разрешает выяснить положение их относительно плоскости проекций и относительно друг друга. Вправду, в случае, если через точку А’ совершить прямую, параллельную направлению si, а через точку А – прямую, параллельную направлению ss, то точка пересечения этих линий и будет данной точкой А (не пересечься эти прямые не смогут, поскольку в другом случае точки А’ и А не могли бы быть проекциями одной точки). Подобным образом возможно отыскать положение точки В и, следовательно, узнать их обоюдное размещение.
Итак, наличие двух проекций объекта может сделать чертеж обратимым.
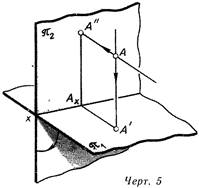
Взять два изображения на одной плоскости при ортогональном проецировании запрещено, поскольку нельзя задать два хороших друг от друга направления проецирования. Исходя из этого проецирование производится на две плоскости проекций – Я1 и яз. Находятся они взаимно перпендикулярно (линия. 5), причем плоскость Л1 – горизонтально и именуется исходя из этого горизонтальной плоскостью проекций, а плоскость-па – перед наблюдателем. Ее именуют фронтальной плоскостью проекций. По окончании проецирования на них объекта плоскости ni и Я2 вращением около линии их пересечения совмещают между собой, образуя одну плоскость чертежа.
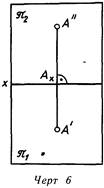
Развернутое изображение в большинстве случаев именуют эпюром* (линия. 6) Линия пересечения плоскостей проекций именуется осью проекций и обозначается на эпюре буквой х. Использование для построения чертежа способа ортогонального проецирования было предложено французским ученым Гаспаром Монжем (1746-1818), что послужило основанием назвать данный способ способом Монжа, а обрисованный выше эпюр эпюром Монжа
На эпюре проекции , каждой изображаемой точки находятся на прямой линии, именуемой линией проекционной связи докажем, что она перпендикулярна к оси проекций
Проецирующие прямые А-А’ и А-А (см линия. 5) образуют плоскость, перпендикулярную к плоскостям Я1 и па и, следовательно, к оси х. Но в случае, если ось х перпендикулярна к плоскости AA’A, то она перпендикулярна к любой прямой данной плоскости, т. е. и к прямым Ax-А’ и А^-А В одной же точке Ах на эпюре возможно восставить единственный перпендикуляр к оси х – линию А’-Ац-А либо А’-А.
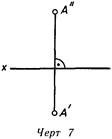
Если не ограничивать плоскости проекций, то эпюр будет иметь вид линия. 7.
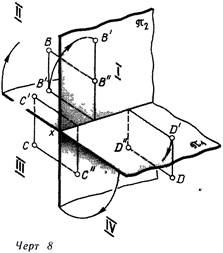
Две плоскости проекций дробят пространство на четыре четверти (линия 8), наряду с этим плоскости, конечно, считаются бесконечными Плоскости дробят друг друга на «полуплоскости», либо «полы» (верхняя пола, нижняя, задняя Четверти и) передняя либо, как их еще именуют, квадранты нумеруют в соответствии с линия. 8.
В большинстве случаев изображаемый объект помещают в первой четверти (точка А, линия 5-7), но видятся случаи, в то время, когда кое-какие его элементы выясняются расположенными и в других четвертях Исходя из этого ознакомимся с эпюрами точек, лежащих во II, III и IV четвертях.
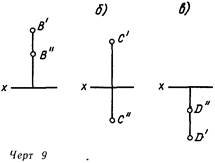
Точка В (линия. 8 и 9, а) находится во 2 четверти. Ее фронтальная проекция будет на верхней поле плоскости V и на эпюре выше оси х. Горизонтальная ее проекция лежит на задней поле плоскости H и по окончании совмещения последней с плоскостью ля окажется также выше оси х Точка С (линия. 8 и 9, б), расположенная в III четверти, спроецируется на нижнюю полу фронтальной плоскости и на заднюю полу горизонтальной, исходя из этого ее проекция С будет на эпюре ниже оси х, а проекция С’ – выше Обе проекции точки D, находящейся в IV четверти, на эпюре лежат ниже оси х (линия. 9, в).
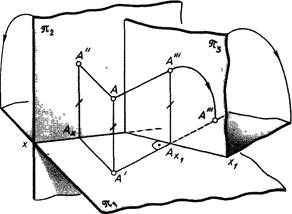
Возвратимся снова к линия. 5 и, сравнивая его с линия. 6, увидим, что фигура AA’AxA – прямоугольник, и на эпюре отрезки [А’-А,}=[А-А} и [А-А,]= =[А-Л’] высказывают собой расстояния оригинала А соответственно от фронтальной и горизонтальной плоскостей проекций. Следовательно, положение точки А по отношению к плоскостям H и Y в полной мере выяснено заданием двух ее проекций. Не обращая внимания на это в практике во многих случаях целесообразно строить дополнительные проекции объектов.
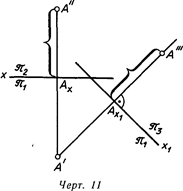
Новую плоскость проекций располагают перпендикулярно к одной из данных плоскостей проекций. На линия. 10 введена дополнительная плоскость проекций яз, перпендикулярная к плоскости Я|. Выстроена третья проекция А’ данной точки А, по окончании чего плоскость яз совмещена с горизонтальной плоскостью Я1 вращением около линии их пересечения. Разумеется, наряду с этим образуется дополнительный эпюр Монжа с осью х\. На этом эпюре проекции точки А
связаны линией проекционной связи Л’— А’, перпендикулярной к оси х\, а отрезки [A’—Ajq] и, [А’—Ах\\ высказывают расстояния точки А соответственно от плоскостейW и H.
На линия. 11 точка А задана проекциями А’ и А в совокупности плоскостей проекций Я1/Я2. Введением дополнительной плоскости W образована совокупность плоскостей проекций H/W с осью х\ и выстроена третья проекция точки А. При построении через А’ совершена линия проекционной связи, перпендикулярная к оси х\, и на ней от точки Ax^ отложено расстояние точки А от плоскости H, которое задано в совокупности плоскостей H/Y отрезком [А—АЛ:
[А-А^] = [А’-АЛ.
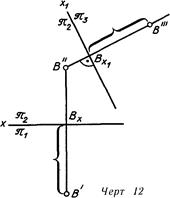
На линия. 12 выстроена третья проекция точки В на плоскости W, перпендикулярной к плоскости V. Для этого через точку В
совершена линия проекционной связи, перпендикулярная к новой заданной оси проекций х\ и от точки B на ней отложено расстояние точки В от плоскости V. В заданной совокупности плоскостей проекций V/H оно равняется отрезку [В’—Вх].
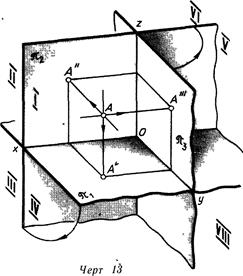
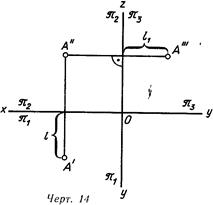
Чаще всего применяют третью плоскость проекций, перпендикулярную к двум данным: W перпендикулярна H, W перпендикулярна V (линия. 13). Такую плоскость именуют профильной плоскостью проекций. Она пересекается с плоскостью H по линии у, а с плоскостьюV— по линии z. Принято совмещать эту плоскость с плоскостью чертежа вращением ее около вертикальной линии z. Наряду с этим получается эпюр, продемонстрированный на линия. 14. Третью проекцию точки строят так же, как это было сделано на линия. 12:
выполняют линию проекционной связи А— А’, перпендикулярную к оси z, и на ней от данной оси откладывают отрезок, равный расстоянию точки А от плоскости эт2, величина которого определяется положением горизонтальной проекции точки А (/!=/).
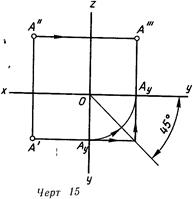
Точку А’ возможно кроме этого взять в пересечении двух линий проекционной связи — линии А —А’ совокупности V/W и линии А’—А’ совокупности H/W (линия. 15). Вторая линия складывается из двух отрезков, что есть следствием принятого правила развертывания в плоскость трехгранного угла, образованного плоскостями H, V и W. Отрезок [А’—Ау] перпендикулярен к изображению оси у на плоскости H (горизонтален), а отрезок [Ay—А’] перпендикулярен к изображению оси у на плоскости W (вертикален). Тождество точек Ау может-быть продемонстрировано дугой окружности, соединяющей их.
При необходимости продемонстрировать на чертеже порядок построения отдельных точек возможно пользоваться еще свойством отрезков линии связи A»—А» пересекаться на некоей прямой, проходящей через точку О и составляющей с горизонтальной линией угол 45° (ее именуют постоянной прямой чертежа). Для данной же цели на линиях проекционной связи наносят стрелки.
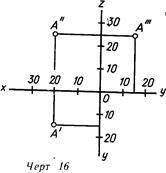
Линии пересечения взаимно перпендикулярных плоскостей проекций смогут быть приняты за оси координат. Поэтому их обозначают буквами х, у и z. В отличие от совокупности ( координат, используемой в математике, в данной совокупности хорошие размеры на оси х откладывают влево от начала координат — точки О. Выбрав ту либо иную величину масштабной единицы, возможно выстроить проекции точек по заданным численным значениям их координат. На линия. 16 выстроены проекции точки. А, имеющей абсциссу х, равную 20 единицам измерения, ординату у, равную 15 единицам, и аппликату z, равную 25 единицам. Меньше это записывается так: Л (20, 15, 25).
Три плоскости проекций дробят пространство на восемь частей, именуемых октантами. Нумерация их продемонстрирована на линия. 13. Как отмечалось выше, мы будем помещать изображаемый объект в первой четверти либо в первом октанте. Так принято делать в СССР и в государствах Европы. При составлении чертежей в государствах Американского континента объект помещают в VII октанте. В европейской проекции объект помещен между каждой плоскостью и наблюдателем проекций, в американской—плоскости проекций отделяют объект от наблюдателя.
ПРОЕКЦИИ ПРЯМЫХ ЛИНИЙ
ПЛОСКОСТЬ
ЗАДАНИЕ и ИЗОБРАЖЕНИЕ ПОВЕРХНОСТЕЙ ИХ НА ЧЕРТЕЖЕ
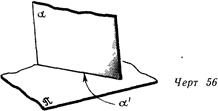
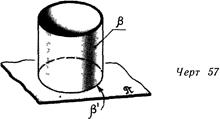
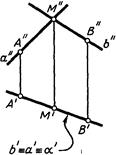
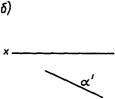
На чертежах (эпюрах) изображают линии и точки (прямые либо кривые) Поверхность возможно изобразить лишь в том случае, если она проецируется линией. На линия. 56 плоскость а, расположенная перпендикулярно к плоскости п, проецируется на нее прямой линией а’. На линия. 57 цилиндрическая поверхность Р проецируется на плоскость я в виде кривой линии у.
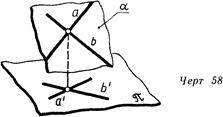
В случае, если плоскость не перпендикулярна к плоскости проекций (линия. 58), изобразить ее нереально. Но ее возможно задать на чертеже, изобразив какие-либо элементы, определяющие ее, к примеру, две пересекающиеся прямые а и Ь (три точки плоскости, прямую и точку, две параллельные прямые).
Подобно задают на другие поверхности и чертежах (см § 26)
ЗАДАНИЕ ПЛОСКОСТИ НА ЧЕРТЕЖЕ
На линия. 59-61 плоскость задана двумя пересекающимися прямыми. На первом – прямыми а и b неспециализированного положения, на втором – горизонтальной hр и фронтальной /р, на третьем – горизонталью и фронталью, выходящими из точки М^, лежащей на оси х. В этом случае горизонтальh лежит в горизонтальной плоскости проекций (нулевая горизонталь), а фронталь f – во фронтальной плоскости проекций (нулевая фронталь) и являются исходя из этого линиями пересечения заданной плоскости с плоскостями проекций (линия. 62). Линии пересечения плоскости с плоскостями проекций именуются следами плоскости, причем ао—горизонтальным следом, а fo —фронтальным.
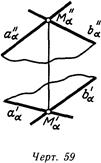
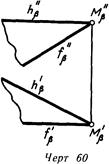
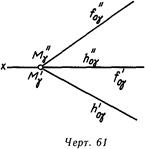
Горизонтальная проекция горизонтального следа сходится с самим следом. (см. линия. 62), а фронтальная— с осью ox Фронтальная проекция фронтального следа сходится с фронтальным следом: foa^foa, а горизонтальная—кроме этого осью х.
Условимся не обозначать на чертежах проекции следов, совпадающие с осью x{ho и /’о), но ‘будем не забывать, что индекс, «нулевая» свойствен горизонтали и фронтали, лежащим лишь в плоскостях проекций.
Линия 62 и 64 дают наглядное представление о плоскостях а и р, заданных следами Не считая следов hо и fo, мы видим тут и профильный след ро линии
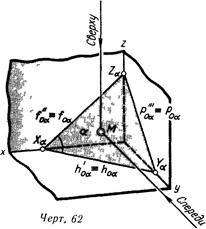
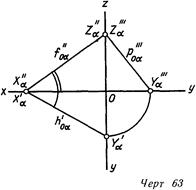
Роа и Ров являются линиями пересечения плоскостей а и (3 с профильной плоскостью проекций Оси проекций пересекаются с плоскостью в точках Хд, Уд и 7д(^в, Ур и Zp), именуемых точками схода следов.
В случае, если, задавая плоскость, возможно произвольно совершить два следа через выбранную точку схода следов, к примеру hy^ и /оа через Хд, то третий след определяется получающимися на осях у и г точками схода следов Уд и Z„ (линия 63 и 65).
Сравнивая линия 62 и 63 с линия 64 и 65, возможно подметить отличие в размещении плоскостей а и (3 по отношению к плоскостям проекций у плоскости а видна спереди и сверху одинаковая ее сторона, у плоскости р — различные стороны Точка (М), расположенная перед плоскостью, в первом случае будет видна и сверху и спереди (будет над плоскостью), во втором случае такая точка сверху видна не будет (находится под плоскостью).
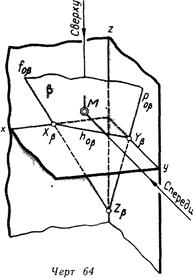
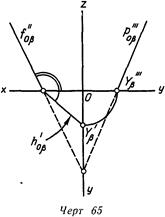
Возможность различать эти плоскости на эпюре разрешит нам в будущем несложнее определять видимость точек довольно заданной плоскости. Исходя из этого назовем условно первую плоскость «остроугольной», а вторую — «тупоугольной» (в соответствии с углами, каковые в первом квадранте образуют между собой следы у плоскости а — острый, у плоскости |3
(тупой)*. На эпюре это выражается тем, что смежные углы между осью х и следами для «остроугольной» плоскости либо оба острые либо оба тупые, а для «тупоугольной» — один острый, а второй тупой.
Ортогональное проецирование
При запасном ортогональном проецировании вводится одна либо большее число дополнительных плоскостей проекций. Любая из них должна быть перпендикулярна к одной из данных либо к снова введенной и размешаться так, дабы интересующая нас фигура (прямая, плоскость и др.) занимала по отношению к ней частное положение.
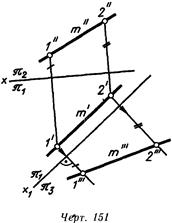
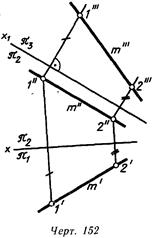
1. Прямая линия неспециализированного положения относительно плоскостей окажется в новой совокупности плоскостей проекций линией уровня, в случае, если новая плоскость проекций лз будет размешаться параллельно ей (линия. 151 и 152).
На линия. 151 введена дополнительная плоскость лз параллельная прямой т и перпендикулярная к плоскости и посредством точек / и 2 выстроена третья проекция прямой т — линия т’. Легко видеть, что в появившейся совокупности плоскостей проекций ж/яз прямая т есть линией уровня.
На линия. 152 дополнительная плоскость яз параллельна прямой — т и перпендикулярна к плоскости . Сейчас прямая т есть линией уровня в совокупности V/W.
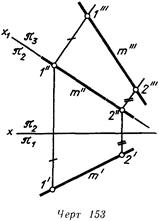
Дополнительная плоскость проекций возможно расположена не только параллельно данной прямой, но и проходить через нее (линия. 153).
, если ось проекции х в совокупность , плоскостей проекций H/V. не зафиксирована (линия 154, а) для построения третьей проекции данной фигуры ее направляться задать Ось возможно совершить произвольно (само собой разумеется, перпендикулярно к линии проекционной связи), но нужно, дабы она была между данными проекциями объекта (см линия 151—153) .
Чтобы прямая линия была проецирующей прямой (т е проецировалась бы на какую или плоскость точкой), должна быть плоскость проекций, перпендикулярная к ней
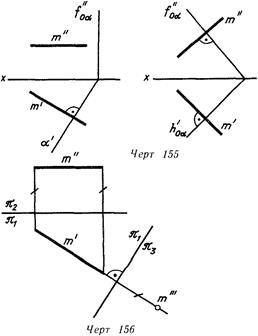
Плоскость проекций, перпендикулярная к одной из данных , возможно перпендикулярна лишь к пря мой частного положения (плоскость, перпендикулярная к прямой неспециализированного положения, есть плоскостью неспециализированного положения, линия 155).
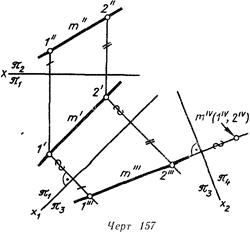
Для прямой же неспециализированного положения требуется введение двух дополнительных плоскостей проекций На линия 157 прямая т спроецирована посредством точек / и 2 нa параллельную ей плоскость. В совокупности плоскостей она есть уже линией уровня. После этого введена четвертая плоскость проекций . В совокупности плоскостей проекций прямая есть проецирующей и четвертое ее изображение является точкой .
Итак, дабы прямая неспециализированного положения была на чертеже в новой совокупности плоскостей проекций проецирующей, нужно ввести две дополнительные плоскости проекций: 3, параллельную прямой, и 4, перпендикулярную ей.
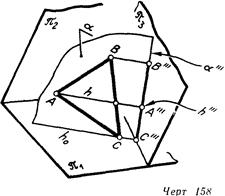
3. Плоскость неспециализированного положения относительно плоскостей H и V окажется в новой совокупности плоскостей проекций, проецирующей, в случае, если новая плоскость проекций будет размешаться ‘ перпендикулярно к ней (линия. 158). Плоскость 3 будет перпендикулярна к плоскости а в том случае, в то время, когда она перпендикулярна к какой-нибудь линии данной плоскости. Прямая неспециализированного положения, лежащая в плоскости а, не может быть таковой линией, поскольку тогда и плоскость 3 будет плоскостью неспециализированного положения (см. линия 155). Но плоскость 3 должна быть перпендикулярна или плоскости H, или плоскости V. Исходя из этого плоскость 3 должна быть перпендикулярна или к горизонтали, или к фронтали плоскости а.
На линия. 158 и 159 введена дополнительная плоскость яз, перпендикулярная к горизонтали h плоскости а (ЛВС) и к плоскости H|, и посредством точек А и В выстроена проекция плоскости а — прямая а». Разумеется, в появившейся совокупности плоскостей проекций H/W плоскость а есть проецирующей.
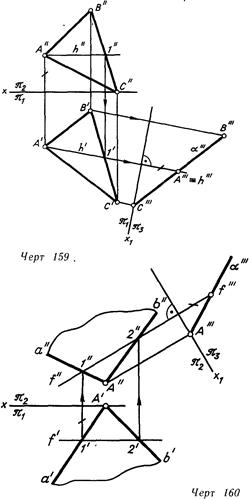
На линия. 160 введена плоскость проекций , перпендикулярная к фронтали данной плоскости а(а(|), которая делается исходя из этого проецирующей в совокупности . В этом примере линия а’ отыскана посредством точек A и l.
Увидим, что в первом случае горизонталь h, а во втором фронталь / проецируются на плоскости 3 в виде точек.
В случаях, в то время, когда эти плоскости выяснены следами, плоскость 3 проводится перпендикулярно к одному из следов.
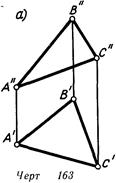
На линия. 161 проекция а.’ плоскости а выяснена точкой схода следов Xia и точкой /, взятой на ее горизонтальном следе.
4. Чтобы эта плоскость была плоскостью уровня, нужно ввести параллельную ей плоскость проекций
(плоскостью уровня именуют плоскость, параллельную плоскости проекций). Разумеется, этого нельзя сделать сходу при данной плоскости неспециализированного положения, но допустимо для проецирующей плоскости.
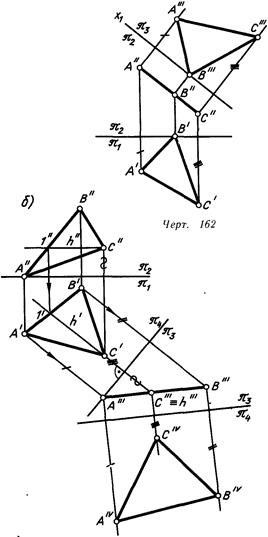
На линия. 162 задана фронтально проецирующая плоскость а (ЛВС) и введена дополнительная, параллельная ей, плоскость проекций лз. В появившейся совокупности плоскостей проекций V/W плоскость а есть плоскостью уровня.
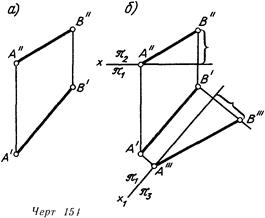
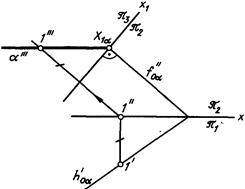
Дабы плоскость неспециализированного положения была плоскостью уровня, требуется сперва ввести такую плоскость проекций Л3, дабы появилась совокупность, в которой плоскость а будет проецирующей. После этого вводится дополнительная плоскость Л4, перпендикулярная к плоскости лз и параллельная плоскости а. На линия. 163, а продемонстрирована заданная плоскость а, а на чертеже 163, б выполнены указанные преобразования.
ОБОЮДНОЕ ПОЛОЖЕНИЕ прямой ЛИНИИ, КРИВЫХ и ПЛОСКОСТИ ПОВЕРХНОСТЕЙ
ОБОЮДНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТИ и КРИВОЙ ПОВЕРХНОСТИ
Плоскость может пересекать кривую поверхность (в частном случае — касается ее) Наряду с этим она имеет с поверхностью неспециализированную линию — линию пересечения поверхностей, воображающую собой в общем случае кривую линию
В случае, если плоскость не имеет неспециализированных точек с кривой поверхностью, то говорят, что она не пересекает данной кривой поверхности
(В этом случае вычисляют линию пересечения поверхностей мнимой )
Из чертежа кривой поверхности и взаимное положение плоскости разумеется лишь в некоторых частных случаях, к примеру, в то время, когда одна из этих поверхностей есть проецирующей
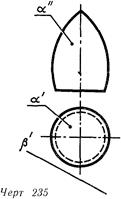
На линия 235 ясно, что поверхность тора а не пересекается с плоскостью р
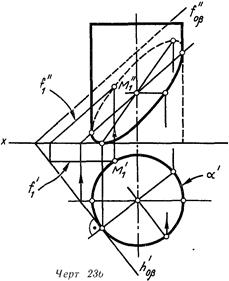
На линия 236 цилиндрическая поверхность а пересекается с плоскостью |3 Наряду с этим линия пересечения поверхностей проецируется на горизонтальную плоскость окружностью, совпадающей с той, в которую проецируется поверхность цилиндра (а’) Фронтальные проекции точек кривой определяются посредством линий плоскости р, проходящих через эти точки. К примеру, точка М выстроена посредством фронтали f .Фронтальные проекции точек соединены посредством лекал
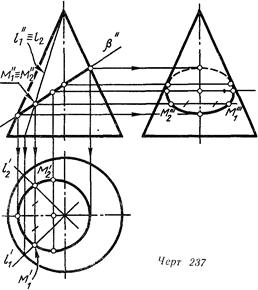
На линия.237 коническая поверхность а пересечена фронтально проецирующей плоскостью ft Фронтальная проекция линии пересечения сходится с проекцией плоскости т==у Горизонтальная проекция строится по точкам, любая из которых
определяется посредством образующей, на которой она находится .
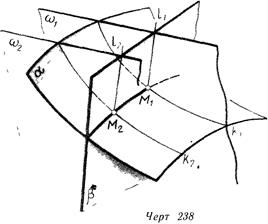
В общем случае для определения линии ‘пересечения кривой поверхности с плоскостью используют способ запасных секущих плоскостей. Проводится последовательность (семейство) секущих плоскостей. Любая из них пересекает кривую поверхность а по линии k, a плоскость р — по прямой линии / (линия 238).
Определяются точки пересечения соответствующих пар линий (в случае, если никакие пары линий не пересекаются, то и поверхности а и р не имеют неспециализированных точек, т. е. не пересекаются). Линия пересечения поверхностей проходит через полученные точки..
Две плоскости пересекаются по прямой линии. Поверхность 2-го порядка пересекается плоскостью по кривой 2-го порядка Поверхность 4-го порядка (поверхность тора) пересекается плоскостью по линии 4-го порядка и т. д.
Увидим еще, что параллельные плоскости пересекают поверхности 2-го порядка по подобным кривым.
Конические сечения
Коническими сечениями именуют линии, получающиеся в следствии пересечения конической поверхности 2-го порядка (в частном случае конической поверхности вращения) плоскостью.
Заданная на линия. 239, а фронтально проецирующая плоскость р пересекает коническую поверхность вращения а по эллипсу (см. кроме этого линия 237).
Вправду, кривая 2-го порядка, получающаяся наряду с этим, не имеет несобственных точек, поскольку все образующие поверхности а пересекаются с плоскостью Р (что разумеется из чертежа). В следствии пересечения поверхности а с плоскостью у, перпендикулярной к оси вращения поверхности, получается окружность—личный вид эллипса.
На линия. 239, б фронтально проецирующая плоскость р параллельна левой очерковой образующей конуса Со всеми остальными образующими поверхности а эта плоскость пересекается (с некоторыми за пределами чертежа). В сечении получается кривая 2-го порядка, имеющая одну несобственную точку е. парабола, т.
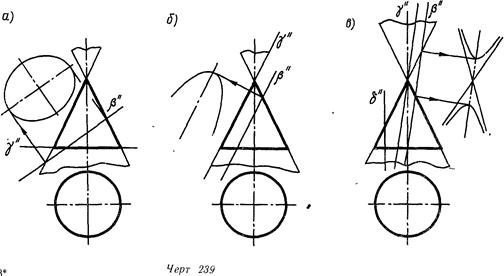
Плоскость -у касается поверхности конуса Касание происходит по образующей, которую возможно разглядывать как несколько параллельных совпадающих прямых. Пара параллельных прямых есть частным видом параболы.
На линия. 239, в плоскость р параллельна двум образующим конуса, расположенным в плоскости у. Остальные образующие его пересекаются с плоскостью (3, причем, кое-какие в точках, расположенных выше вершины конуса, т. е. на верхней его поле. Кривая 2-го порядка, получающаяся в этом случае, имеет две несобственные точки и есть исходя из этого преувеличением. Легко видеть, что эта кривая имеет две части (ветви), одна из которых расположена на нижней части конической поверхности, вторая — на верхней. Плоскость у, проходящая через вершину конуса, пересекает поверхность по паре образующих, являющихся частным видом преувеличения
Плоскость 6,параллельная оси конуса, а следовательно, и двум образующим поверхности, пересекает коническую поверхность также по преувеличению.
Определения и ОБЩИЕ Понятия
При построении эпюра предмета* последний в большинстве случаев располагают так, дабы направления трех основных измерений его были параллельны плоскостям проекций (линия. 349): направление длины — параллельно оси х, ширины — оси у и высоты — оси z. Тогда высота и длина проецируются в натуральную величину на фронтальную плоскость проекций, ширина и длина не искажаются на горизонтальной проекции, а высота и ширина — на профильной. Таковой чертеж нетрудно строить, по , нему измерения, делать выводы о размерах изображенного, предмета. Но он недос1аточно нагляден. На каждой из проекций отсутствует одно из трех измерений. Дабы воспроизвести форму предмета, нужно в мыслях воссоздать ее по двум, трем, а время от времени и большему числу проекций.
Более наглядный чертеж возможно взять, проецируя предмет на одну плоскость проекций и располагая его так, дабы ни одно из направлений основных измерений не проецировалось точкой.
На линия. 350 изображен такой же параллелепипед, как и на линия. 349, но протяженность, высота и ширина его воспринимаются по одной проекции, поскольку взор «охватывает» сходу три стороны предмета По такому чертежу легко представить себе его форму.
Но второй чертеж владеет двумя значительными недочётами: во-первых, он необратим, поскольку представлена лишь одна проекция предмета; во-вторых, по чертежу нельзя произвести измерения предмета.
Дабы ликвидировать первый недочёт, чертеж дополняют второй проекцией, именуемой вторичной.
Дабы чертеж стал измеримым, на нем строят изображение совокупности координат Oxyz, оси которой параллельны соответственно
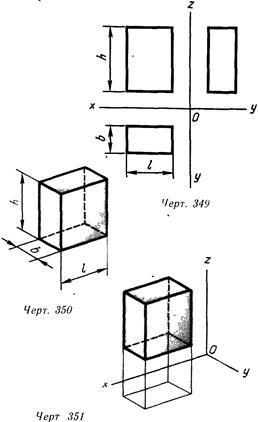
направлениям длины, высоты и ширины изображаемого предмета (линия. 351). В случае, если известно, как искажаются размеры по осям х, у и z, то по чертежу возможно делать выводы о размерах предмета. Выстроенный так чертеж именуют аксонометрическим либо аксонометрией.
показатели искажения и Аксонометрические оси. Для построения аксонометрических чертежей нужно знать, как проецируются оси совокупности координат хугО (т. е. три взаимно перпендикулярные линии, проходящие через одну точку) и единичные отрезки, взятые на них.
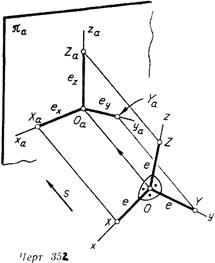
Разглядим линия. 352. Координатные оси совокупности Oxyz и отрезки на них [Х—0], [У—О] и [Z—0], равные натуральной единице е, спроецированы по направлению s на плоскость проекций Ла. В следствии взяты аксонометрические оси Xa. ya, Za, On и аксонометрические единицы вг, ёу, вг (в будущем индекс «а» у аксонометрических проекций опускается).
Отношения
именуют показателями искажения соответственно по осям Xa, Уа и Z„ аксонометрии. Показатели искажения связаны соотношением
Вторичные проекции. Для получения второй проекции на плоскости Ла изображаемый объект предварительно проецируют на одну из координатных плоскостей. После этого взятую проекцию (вместе с осями координат) проецируют на плоскость Ли. Сообщённое поясняет линия. 353. Точка А (объект) спроецирована сперва на плоскость хОу. Взятую проекцию А’ проецируют после этого на плоскость Л.. В конечном результате на аксонометрическом чертеже получаются два изображения точки А: Аа и А’а (вторичная), каковые в полной мере определяют ее положение относительно системы координат Oxyz.
Виды аксонометрических проекций. Аксонометрическая проекция именуется косоугольной, в случае, если направление проецирования s не перпендикулярно к плоскости проекций (о=т’=90°).
Аксонометрическая проекция именуется прямоугольной, в случае, если направление проецирования s перпендикулярно к плоскости Ла(о=90°).
Помимо этого, различают:
1. Триметрические проекции. Все показатели искажения тут разны
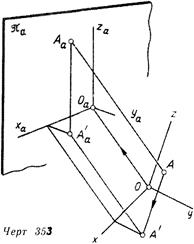
2. Диметрические проекции Два показателя искажения равны, третий — не равен им. Наряду с этим вероятны три случая: a) u=v^=w, б) и=/=и=гр и в) u=^-v^=w=u..
1. Изометрические проекции. Все показатели равны:
УНИВЕРСИТЕТ ЭКОНОМИКИ, УПРАВЛЕНИЯ И ПРАВА (г.Казань)