Обнаружение лучшего варианта эконометрической модели в большинстве случаев осуществляется методом сравнения соответствующих им качественных черт, каковые возможно вычислить на базе исходной статистических данных, содержащейся в векторе у, матрице Х, и новой расчетной информации, появляющейся по окончании построении каждого из вариантов модели. Логика в ответе этого вопроса достаточно несложная: лучшему варианту модели в общем случае должны соответствовать и лучшие значения черт его качества.
Тут направляться подчернуть, что главным высококачественным условием “” модели есть обоснованность “математической формы функционала f(a, xt ), как по составу включенных в него свободных переменных, так и по виду их связей с зависимой переменной уt, в совокупности определяющих обстоятельства ее изменчивости. В данной связи, новая информация, показавшаяся по окончании построения функционала f(a, xt), разрешает установить, как удалось реализовать это условие на практике.
Отметим главные подходы к оценке “качества” эконометрических моделей.
Ведущая роль при определении черт качества эконометрической модели в собственности последовательности ее “выборочной” неточности еt, t =1, 2,…, Т, что формируется с применением отысканных оценок ее параметров как
где – расчетное значение переменной у в момент t, определенное в общем случае как = f (a, xt ) по окончании подстановки в функцию f (a, xt ) значений оценок параметров a0, a1,…, an и известных значений свободных переменных хit, i=1, 2,…, n, t=1, 2,…, Т. К примеру, для линейной модели (1.2) значения определяются на основании следующего выражения:
В данной связи напомним, что для каждого комплекта оценок параметров a0, a1, a2,… того либо иного варианта модели, обрисовывающей разглядываемый процесс, рассчитывается “собственный” последовательность неточности et, t=1, 2,…, Т, что возможно трактовать как последовательность оценок ее подлинных, но малоизвестных значений et (см. (1.1)).
На первый взгляд, соответствие модели особенностям процесса и точность его аппроксимации малоразличимые между собой понятия. К тому же, в их основе лежат разные представления о мерах процесса и адекватности модели. С применением способов построения многочленов, к примеру, проходящих через заданные точки (задача интерполяции), возможно подобрать такое уравнение f(a, xt ), что его значения в точках t=1, 2,…, Т в точности совпадут с замечаемыми значениями зависимой переменной уt. Все значения неточностей в этом случае будут равны нулю еt=0, t=1, 2,…, Т. Но это уравнение фактически ни при каких обстоятельствах не будет высказывать неспециализированную тенденцию переменной уt, сформировавшуюся под влиянием свободных факторов хi, i=1, 2,…, n; ни в промежутках между их зафиксированными в моменты t=1, 2,…, Т значениями, ни тем более в прошедшие и будущие периоды времени (см. рис. 1.3). Уравнение f (a, xt ) в этом случае будет высказывать тенденцию интерполирующего многочлена, а не настоящего процесса уt.
Высказывая уравнением f (a, xt) неспециализированные закономерности процесса уt, фактически нереально добиться совпадения его значений и замечаемых уровней зависимой переменной уt в п-мерной точке xt, потому, что, как было отмечено ранее, данный функционал не учитывает второстепенные обстоятельства изменчивости переменной у, исходная информация не совершенно верно отражает разглядываемые явления и т. п. Но, в случае, если вид функционала f(a, xt) в целом соответствует неспециализированным закономерностям изменчивости переменной уt, на промежутке t=(1, Т), то возможно сохранять надежду, что это соответствие имело место и в прошлом (т. е. при t?0), и на промежутках (t, t+1) и, что более принципиально важно, сохранится и в будущем (при t³Т+1). Это есть “определенной гарантией” того, что применение функционала f(a, xt) в ответе прогнозирования процесса и задач управления уt не приведет к важным неточностям.
уt
кривая, соответствующая функционалу, опи-
сывающему неспециализированную тенденцию переменной уt
измеренные значения переменной уt
кривая, соответствующая интерполирующему
функционалу f ( a , xt ),
xt
Рис. 1.3. Различие между интерполирующим и обрисовывающим
неспециализированную тенденцию переменной уt вариантами функционалаf (a , xt )
Вместе с тем разумеется, что среди нескольких разных вариантов функционала f(a, xt), приблизительно одинаково отражающих неспециализированные тенденции процесса уt, более предпочтительным есть тот из них, что снабжает и лучшую аппроксимацию (в математическом понимании этого термина).
В общем случае “уровень качества” эконометрической модели оценивается по двум группам черт, не смотря на то, что, как это будет продемонстрировано потом, предполагаемая группировка не в полной мере однозначна, потому, что, во-первых, характеристики каждой из групп довольно часто имеют двойное назначение, а, во-вторых, многие из них взаимосвязаны между собой. В первую из групп включим показатели, критерии, высказывающие “степень” соответствия выстроенной модели главным закономерностям обрисовываемого ею процесса. Во вторую – критерии и показатели, в основном оценивающие точность ее аппроксимации замечаемых значений процесса уt .
В данной связи направляться подчернуть, что к параметрам первой группы смогут быть отнесен и критерий Стьюдента, применяемый для оценки значимости влияния каждого из факторов хi, i=1, 2,…, n, на зависимую переменную уt (см. раздел 1.3).
Соответствие эконометрической модели обрисовываемому ею процессу уt в значительной мере возможно установлено на базе анализа особенностей вычисленного последовательности неточности et, t=1, 2,…, Т*. В случае, если вариант модели “правильно” отражает главные тенденции процесса уt , то возможно ожидать, что значения неточности в определенной степени случайны, их свойства близки к особенностям процесса “белого шума”. В случае, если же тенденция, закономерности процесса уt учитываются моделью не полностью (в модель не включены какие-либо значительные с содержательной точки зрения факторы, выбрана форма функционала f(a, xt), не адекватная характеру связей между разглядываемыми переменными и т. п.), то в последовательности неточности в большинстве случаев появляется некая закономерность, свидетельствующая об потере свойства ее “случайности”. Увидим, что “неслучайный” темперамент фактической неточности модели et возможно предопределен и неверно выбранным способом оценки параметров модели.
Забегая вперед, напомним, что среди способов оценки параметров линейных эконометрических моделей громаднейшее распространение взяли способ большого правдоподобия, способ мельчайших квадратов и способ моментов. Любой из них употребляется при в полной мере определенных исходных предпосылках относительно свойств неточности модели et. К примеру, хорошие варианты этих способов употребляются в предположении, что неточности совпадают со особенностями процесса “белого шума” (нулевое среднее, конечная дисперсия, отсутствие автокорреляционных связей). Наряду с этим “способ большого правдоподобия” предполагает известным закон распределения неточности. Значительно чаще употребляется предположение о “нормальности” ее распределения. В данной связи выстроенная с применением способа большого правдоподобия модель будет принимать во внимание адекватной разглядываемому процессу, в случае, если свойства фактической неточности et, определенной в соответствии с выражению (1.27), будут не через чур очень сильно различаться от предполагаемых особенностей неточности et (“белого шума” с обычным распределением).
Способ мельчайших квадратов не выдвигает столь твёрдых требований к закону распределения неточности. В соответствии с ему оценки параметров моделей определяются исходя из критерия минимума суммы квадратов неточности. В таковой ситуации модель, выстроенная с применением данного способа, будет принимать во внимание адекватной разглядываемым процессам, в случае, если ее неточность по своим особенностям аналогична “белому шуму”.
В случае, если в отношении неточности эконометрической модели et выдвигаются предположения, что ее свойства хороши от особенностей “белого шума”, то для оценки параметров модели в большинстве случаев употребляются так именуемые обобщенные модификации данных способов.
Отличие неточности модели от “белого шума” может выражаться, к примеру, непостоянством ее дисперсии на разных участках промежутка t=1, 2,…, Т; наличием связи между ее соседними значениями, высказываемыми, к примеру, уравнением следующего вида et =b?et–1+xt, где xt – новая неточность, по своим особенностям близкая к процессу “белого шума” и т. п.
Но на практике для моделей многих типов такие свойства неточности модели априорно предвидеть в большинстве случаев не представляется вероятным. Их возможно установить, лишь разбирая свойства фактической неточности et, взятой для моделей, оценки коэффициентов которых выяснены с применением “хороших” способов оценивания.
Так, наличие либо отсутствие свойства “случайности” в последовательности выборочной неточности модели et, t =1, 2,…, Т; в определенной мереуказывает на “соответствие” либо “несоответствие” модели обрисовываемому ею процессу у. В том случае, в то время, когда неточность модели “неслучайна”, возможно рекомендовано уточнить разглядываемый вариант модели, выбрать более подходящий для данной обстановки способ оценки ее параметров.
Как было отмечено выше, “неслучайность” неточности может иметь разный темперамент. Чаще всего она выражается наличием автокорреляционной связи между соседними ее значениями, тенденциями, характеризующими трансформации их квадратов, т. е. тенденциями в последовательности et2, t=1, 2,…, Т и других ее производных. Для обнаружения “неслучайности” в последовательности неточности модели в большинстве случаев применяют своеобразные тесты, многие из которых будут рассмотрены в последующих главах книжки применительно к моделям соответствующих типов. Тут же как пример обрисуем изюминке применения для этих целей достаточно универсального теста (критерия) Дарбина-Уотсона. Он самый активно используется в эконометрических изучениях благодаря собственной простоты, не смотря на то, что и не владеет значительной эффективностью (достоверностью). Тест Дарбина-Уотсона в большинстве случаев употребляется для установления факта наличия автокорреляционной зависимости первого порядка в последовательности неточности et, т. е. между соседними ее значениями, et и et+1, t=1, 2,…, Т. В большинстве случаев соседние значения неточности связаны более сильной зависимостью, чем значения et и et+2, et и et+3 и т. д. Благодаря этого отсутствие автокорреляционной связи между последовательностями значений выборочной неточности et и et–1, t=1, 2,…, Т–1; разрешает с громадной степенью уверенности утверждать, что в последовательности подлинной неточности модели et отсутствуют по большому счету какие-либо автокорреляционные связи.
Значение критерия Дарбина-Уотсона рассчитывается по следующей формуле
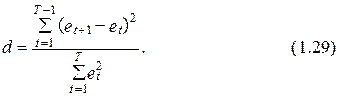
Раскрывая квадрат в числители выражения (1.29), возьмём:
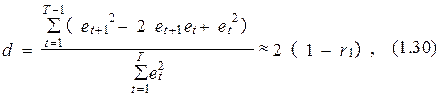
где r1– коэффициент автокорреляции первого порядка неточности et, т. е. корреляции между последовательностями et и et+1.
Из выражения (1.30) конкретно вытекает, что
0 ? d ? 4. (1.31)
Значение d=0 соответствует случаю, в то время, когда между последовательностями et и et+1существует строгая хорошая линейная зависимость, т. е. r1=+1, и значение d=4 соответствует строгой отрицательной связи, r1=–1. В случае, если последовательности et и et +1свободны, то r1=0 и d=2.
Точки d=0; 2; 4 и определяют границы критерия Дарбина-Уотсона, в пределах которых догадка о наличии автокорреляции первого порядка в последовательности неточностей или принимается (в регионах родных к 0 либо 4), или отвергается (в области d=2), или ответ по этому критерию неопределен (в промежутках между отмеченными областями). Иными словами, на отрезке [0,4] выделяются четыре промежуточные точки, так, что 0?d1?d2?2?d3?d4?4. В случае, если расчетное значение критерия Дарбина-Уотсона находится на отрезках [0, d1] , [d4,4], то догадка о наличии автокорреляции первого порядка в последовательности неточностей модели принимается, в случае, если расчетное значение d находится в промежутке [d2, d3], – то отвергается. Значения d, приходящиеся на полуинтервалы [d1, d2] и [d3, d4], не разрешают сделать однозначного суждения по данной догадке. В последнем случае нужно проводить более глубочайший анализ зависимостей между значениями неточности et, t=1,2,…, Т.
Другую группу параметров, в основном направленных на обнаружение степени точности аппроксимации функционалом f(a, xt ) замечаемых значений зависимой переменной уt, образуют обширно применяемые в эконометрике и статистике коэффициент множественной корреляции R, коэффициент детерминации D, критерий Фишера F.
Тут направляться подчернуть, что общепринятой в статистике мерой точности “аппроксимации” есть дисперсия (в нашем случае дисперсия модели). Ее значение на практике в большинстве случаев определяется на основании следующей формулы:
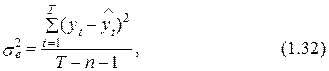
где =f (a, xt) – рассчитанные на основании уравнения модели f(a, xt) значения зависимой переменной, Т– количество измерений, п+1 – число параметров модели.
Но значение дисперсии не отражает многих значительных качеств качества модели и, помимо этого, оно не весьма пригодно для целей содержательного анализа.
Несложно подметить, что величина неточности тесно связана с уровнем зависимой переменной у, и в данной связи она имеет “безотносительное” содержание. Одновременно с этим “точность” в основном относительна. Исходя из этого меньшее значение дисперсии еще не говорит о более высоком “качестве” модели, ее аппроксимирующих возможностях. Громадная дисперсия может высказывать только более большие уровни свободной переменной, а не ухудшение точности ее аппроксимации выстроенной моделью.
Тут направляться подчернуть, что и “относительность” неточности может рассматриваться в двух качествах. Во-первых, по отношению к уровню переменной у, а, во-вторых, – к некоему уже установленному “эталону” точности. Именно эти нюансы в основном и учитывают коэффициенты и указанные критерии.
Коэффициент множественной корреляции показывает степень приближения расчетных (по выстроенной модели) значений зависимой переменной (a, xt) к настоящим ее значениям уt . Величина коэффициента множественной корреляции изменяется в пределах от нуля до единицы (0? R?1). Значения R,родные к нулю, говорят о том, что расчетные значения не хорошо аппроксимируют значения уt. В случае, если R близок к единице, то это указывает, что модель отлично аппроксимирует исходный последовательность значений уt, t=1, 2,…, T.
Значения коэффициента детерминации кроме этого находятся на отрезке [0,1], 0?D?1. Его конкретная величина показывает долю изменчивости переменной у, растолковываемую включенными в модель факторами хi, i=1, 2,…, n. К примеру, в случае, если D=0,81, то это указывает, что включенные в модель переменные растолковывают 81% изменчивости переменной уt, а другая ее изменчивость разъясняется неучтенными в модели обстоятельствами.
Значения коэффициентов множественной корреляции и детерминации рассчитываются на основании следующего выражения*:
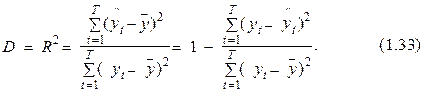
Обоснование целесообразности применения коэффициента детерминации при определении качества выстроенной эконометрической модели содержится в следующем. “Успешная“ модель обязана “растолковывать” главные закономерности изменчивости зависимой переменной уt. Количественной мерой данной изменчивости в статистике принято вычислять показатель, рассчитываемый на основании следующей формулы:
Увидим, что отличие является отклонением значения уt от среднего уровня данной переменной, а неспециализированная изменчивость, так, выражается в виде суммы квадратов всех таких отклонений. По окончании определения и построения модели на ее основании “расчетных” значений , каждое из таких отклонений возможно представить в виде суммы двух составляющих
Первое из слагаемых правой части выражения (1.35) представляет собой расчетное значение неточности модели в момент t, т. е. . Второе слагаемое высказывает отклонение этого расчетного значения от среднего уровня переменной уt. С учетом (1.35) выражение (1.34) возможно записать в следующем виде:
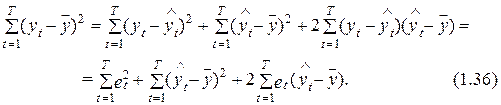
Как будет продемонстрировано во II главе, неточность et владеет рядом особенностей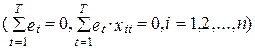 
, применяя каковые возможно доказать, что последняя сумма в правой части выражения (1.36) равна нулю. Отсюда вытекает, что неспециализированная изменчивость переменной уt кроме этого возможно представлена в виде двух составляющих
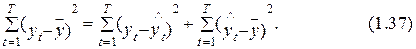
Наряду с этим первая из них
высказывает сумму квадратов неточности модели, т. е. часть изменчивости переменной уt, необъясненную выстроенной моделью, а второе слагаемое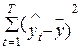 
– часть изменчивости переменной уt , которую выстроенная модель растолковала.
Поделив левую и правую части выражения (1.36) на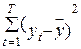 
, возьмём
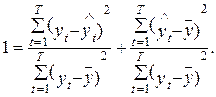
Из последнего выражения следует (1.33), т. е.
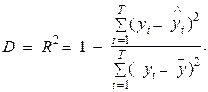
Так, в случае, если модель полностью совершенно верно соответствует исходному последовательности зависимой переменной уt, т. е. расчетные значения f(a, xt) равны уt для всех t =1, 2,…, T, то D=R=1.
В тех случаях, в то время, когда модель не имеет возможности ни в какой мере растолковать изменчивость переменной уt, имеем R=D=0. При линейной форме зависимости f(a, xt) это происходит, к примеру, в тех случаях, в то время, когда значения уt равномерно распределяются около линии параллельной оси Х (см. рис. 1.4 (а, б)), что влечет за собой равенство , t=1, 2,…, T.
Из изложенного выше направляться, что высокие значения переменных D и R ассоциируются с хорошей степенью аппроксимации выстроенной эконометрической моделью f(a, xt) исходного (заданного) последовательности значений зависимой переменной уt, t=1, 2,…, T, а низкие значения – с нехорошей аппроксимацией. Вместе с тем направляться иметь в виду, что обстоятельства нехорошей аппроксимации смогут быть различные. В одних случаях это происходит из-за неверного выбора растолковывающих (свободных) переменных, в других – из-за неправильно подобранной формы уравнения модели.
| фактические значения у |
у у
 |
|||
 |
|||
| расчетные значения у |
х х
а) б)
Рис. 1.4(а,б). Примеры распределения переменной уt , при которых линейная эконометрическая модель) = a0+ a1х1t имеет корреляции и нулевые коэффициенты детерминации.
Так, к примеру, в случае, если для переменной уt, фактические значения которой обозначены прерывистой линией на рис. 1.4(а) в качестве эконометрической модели применять уравнение эллипса а для переменной уt на рис. 1.4(б) – уравнение синусоиды то точность описания разглядываемых процессов была бы существенно выше и характеристики D и R были бы родными к единице.
Критерий Фишера (F-критерий) кроме этого употребляется для определения надежности всей модели методом сопоставления ее меры неточности с величиной меры рассеяния переменной уt относительно Величина этого критерия определяется по формуле
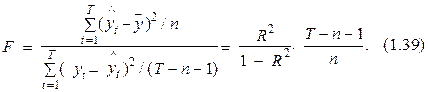
Целесообразность применения критерия Фишера возможно обосновать, заменив в выражении (1.39) показатель R2 на его модификацию – скорректированный квадрат коэффициента множественной детерминации , рассчитываемый с учетом замены изменчивости квадратов и суммы ошибки переменной уt на соответствующие дисперсии. Значение рассчитывается в соответствии с следующей формулы:
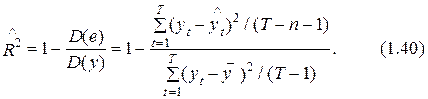
Наряду с этим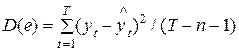 
является дисперсией неточности et (см. (1.32)), где Т–п–1 – число степеней свободы, учитываемое при ее определении (Т– число измерений, п+1 – количество связанных параметров-коэффициентов модели); 
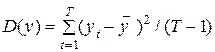– дисперсия переменной уt, Т–1 – число степеней свободы при одном связанном параметре .
На основании (1.33) и (1.40) связь между квадратами коэффициентов множественной корреляции R2 и возможно представить в виде следующего соотношения:
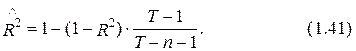
Скорректированный коэффициент как мера качества выстроенной модели имеет определенные преимущества если сравнивать с его предшественником – коэффициентом R2. В частности, из выражения (1.40) вытекает, что включение в модель свободных факторов, неважных с позиций объяснения изменчивости переменной уt, может вести к уменьшению значения (см. числитель дробной части (1.40)). Одновременно с этим показатель R2 не чувствителен к трансформации количества таких переменных.
Тут нужно подчернуть, что критерий Фишера может рассматриваться и в качестве “меры” обоснованности включения в эконометрическую модель всей совокупности свободных переменных. В этом случае его возможно отнести и к параметрам первой группы, характеризующим степень соответствия выстроенной модели исследуемому процессу уt.
Критерий Фишера в таковой ситуации рассматривается как собственного рода тест при проверке догадки, что ни один из свободных факторов не играется никакой роли в объяснении изменчивости переменной уt либо, что то же самое, все коэффициенты при свободных факторах модели равны нулю (a1=0, a2=0,… , aп =0) (см. раздел (2.2)). В соответствии с этим отношение R2/п в выражении (1.39) представляет собой среднюю долю растолкованной изменчивости переменной уt, приходящуюся на один свободный фактор, а (1–R2)/(Т–п–1) – среднюю долю необъясненной изменчивости переменной уt, в расчете на одну степень свободы.
При слабом влиянии свободных факторов на переменную уt (т. е. при ai ®0, i=1,2,…, n) значение R2, как и величина критерия F пытается к нулю, и, напротив, с повышением R2 численное значение F кроме этого возрастает. Увидим, что показатель F есть случайной величиной, являющейся отношение двух дисперсий. Эта величина распределена по закону Фишера с п и Т–п–1 степенями свободы (F(п, Т–п–1)). Благодаря этого на практике проверка значимости коэффициентов модели с применением критерия Фишера пребывает в сопоставлении его расчетного значения, определенного для выстроенного варианта модели по формуле (1.34), с табличным значением F*(п, Т–п–1), соответствующим заданному уровню доверительной возможности р* (возможности неточности первого рода 1–р*) и известным степеням свободы п и Т–п–1.
В случае, если выясняется , что
F
то догадку о незначимости совокупного влияния свободных факторов на переменную уt целесообразно принять (возможность ее осуществления равна р*). В другом случае роль факторов в объяснении изменчивости переменной уt направляться признать значительной. С ростом F эта роль согласится все более значимой.
Критерий Фишера возможно применять и при сравнении качества (точности описания исходного процесса уt) двух разных других вариантов модели. В этом случае его величина рассчитывается по формуле
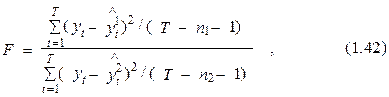
где =f1(a1, xt1), =f 2(a2, xt2) – расчетные значения переменной у, полученные на базе первого и второго вариантов моделей соответственно, различающиеся, возможно, формой зависимости f и числом факторов х; n1 и n2 – количества факторов в первом и втором вариантах соответственно.
Критерий (1.42) есть двухсторонним. Особенности его применения пребывают в следующем. В случае, если выполняется соотношение
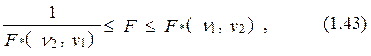
то разглядываемые другие варианты модели будут считаться равнозначными с позиций точности описания процесса уt.
В случае, если
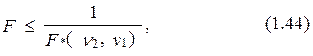
то выбор необходимо осуществить в пользу первого варианта модели, а вдруг
то – в пользу второго.
F*(n1, n2) – табличное значение критерия Фишера, выбранное для заданного уровня доверительной возможности р* и числе степеней свободы n1=Т–n1–1 и n2=Т–n2–1.
Подводя итог данного раздела еще раз обратим внимание на определенные содержательные и количественные связи между показателями качества и критериями эконометрической модели разных групп. К примеру, напомним, что появление автокорреляционных связей у значений неточности, по большому счету говоря, делает вышеприведенные выражения параметров Фишера, коэффициента детерминации, множественных коэффициентов корреляции и т. п. некорректными. Это обусловлено тем, что применяемая при расчете их значений сумма квадратов неточности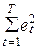 
не имеет возможности рассматриваться как “мера точности аппроксимации” заданного последовательности значений уt, потому, что не учитывает, к примеру, автокорреляционные связи между разновременными неточностями et и et+i, i=1, 2,…* Критерии Стьюдента и Фишера, коэффициенты множественной корреляции и детерминации, отнесенные к различным группам, довольно часто употребляются совместно при обосновании выбора варианта эконометрической модели. Это связано с тем, что любой из включенных в модель факторов, в большинстве случаев, растолковывает некую долю изменчивости зависимой переменной уt, пускай кроме того и маленькую. Благодаря этого, в то время, когда свободных факторов не через чур много и между ними не отмечается сильных связей, то исключение из их состава кроме того малозначимого с позиций критерия Стьюдента фактора объективно сокращает количество информации, растолковывающей изменчивость уt. Это, со своей стороны, влечет за собой уменьшение значений черт D, R и F. Может появиться такая обстановка, в то время, когда, удалив на следующем шаге незначимый фактор, исследователь приобретает менее успешный по этим показателям вариант модели. В случае, если нет вторых других ее вариантов, то появляется неприятность выбора между “ненадежным” вариантом модели со значимыми факторами и более надежным вариантом, у которого кое-какие из свободных переменных незначимы. На практике в большинстве случаев выбор делается в пользу более “успешной” модели, потому, что более правильное описание процесса уt в эконометрике есть и более предпочтительным если сравнивать с ответом задачи установления списка значимых по степени влияния на переменную уt факторов.
Так, этапы формирования модели (обоснование формы функционала, состава свободных переменных) и оценки ее качества в значительной мере взаимосвязаны между собой. Для них, в большинстве случаев, нельзя установить твёрдую очередность. Довольно часто информация, полученная на “более поздних этапах” заставляет производить перерасмотрение итоги прошлых. Увидим кроме этого, что ключевую роль на всех этих этапах играется содержательная сторона неприятности. Не подкрепленные результатами содержательного анализа и основанные лишь на “хороших” количественных параметрах варианты эконометрических моделей довольно часто являются с практической точки зрения ненужными, малосодержательными “аппроксимациями”.
Вместе с тем уровень качества модели в значительной мере зависит от того, как “успешны” оценки коэффициентов модели ai , i=0,1,… п. Они играются, пожалуй, главную роль при обосновании ее “качества”, потому, что на базе их значений конкретно определяется одна из наиболее значимых составляющих модели, характеризующих ее уровень качества, – выборочная неточность.
Главные подходы к обоснованию “качества” оценок параметров эконометрической модели рассмотрены в следующем параграфе книжки.