В этом классе задач приходится оперировать таким типом данных, как строки, проводить преобразования строковых данных в числовые и напротив.
Задача 3.1
Для заданной строчка знаков проверить, есть ли она симметричной либо нет. (Симметричной считается строчок, которая одинаково читается слева направо и справа налево).
Задача 3.2
Для заданной строчка знаков проверить, есть ли она палиндромом (симметричной с точностью до пробелов) либо нет.
К примеру, палиндромами являются цепочки:
АРГЕНТИНА МАНИТ НЕГРА
А РОЗА УПАЛА НА ЛАПУ АЗОРА
(Предполагается, что все буквы строчка — прописные).
Задача 3.3
Для заданной строчка знаков выяснить сумму всех входящих в неё цифр.
Задача 3.4
Для заданной строчка знаков вычислить произведение входящих в эту строчок целых чисел (не учитывая их знаков). К примеру, для строчка kjjjkkj2.5jkjn,,,hfd45jgfvjlkfdii10,2hfhg произведение 2*5*45*10*2=9000.
Задача 3.5
Для заданной строчка знаков вычислить сумму входящих в неё цифр, причем символ очередного слагаемого должен быть противоположным символу прошлого слагаемого.
К примеру:
Для строки asdd1vnb24vnf63vbn,-5h-2kk
Сумма S=1-2+4-6+3-5+2= -3.
Задача 3.6
Для заданной строчка знаков отыскать громаднейшее записанное в данной строке целое число (не учитывая символа числа). К примеру, для строчка sdfvgsd1.9fdmjgvb-15.2dnj05 солиднейшее целое число 15.
Задача 3.7
Для заданной строчка выяснить все входящие в неё знаки. К примеру: строчок abccbbbabba складывается из знаков a,b и с.
Задача 3.8
Задана строчок знаков. Среди литер этого текста особенную роль играется символ #, появление которого свидетельствует отмену прошлой литеры текста; k знаков # отменяют k прошлых литер (в случае, если такие имеется) Напечатать строчок с учетом роли символа #. К примеру, строчок VR#Y##HELO#LO должна быть напечатана в виде: HELLO.
Задача 3.9
Задана строчок знаков. Выяснить, какой знак видится в данной строке подряд наибольшее число раз. В ответе указать знак, образующий самую долгую последовательность, номер символа и длину последовательности, с которого она начинается.
К примеру, в строчке asadddbbbbababaaaaaahhgg знак a образует последовательность длиной в 6 знаков, начиная с знака с номером 15.
Задача 3.10
Для заданной строчка знаков, складывающейся из пробелов и строчных букв, выяснить слово громаднейшей длины, которое начинается и заканчивается на одну и ту же букву. К примеру: строчок — револьвер совокупности наган, слово — револьвер.
Задача 3.11
В символьной строке имеются круглые скобки. Проверить, верно ли они расставлены.
Задача 3.12
Заданы две строки. Выяснить, являются ли они анаграммами, другими словами одна строчок взята из второй перестановкой букв.
К примеру:
строки КУБ и БУК либо СОЛЬ и ЛОСЬ являются анаграммами.
Задача 3.13
Отыщем в памяти игру: Придумай слово, в которой из букв слова-донора составляют другие слова. К примеру, из слова МОНИТОР возможно взять МОТОР, РОТ, ТИР и др. Вхождение каждой буквы в новое слово допускается не более того числа раз, с каким она входит в слово-донор.
Пускай дана последовательность слов, поделённых пробелами в виде строчка знаков. Как мы знаем, что первое слово в данной строке есть донором. Выбрать из оставшихся слов последовательности те, каковые возможно взять из заданного слова-донора.
Задача 3.14
Задана строчок знаков, содержащая два либо более слов, поделённых пробелами. Разработать программу, меняющую местами все четные и нечетные слова в строчке, предполагая, что за один раз возможно поменять местами не более двух знаков.
Решения задач
Задача 3.1
Несложнее всего в данной задаче выяснить длину строчка n, организовать цикл по номеру знака в строчке и сравнивать попарно первый знак с последним, второй — с предпоследним и т.д. В случае, если хотя бы одна пара разна, то строчок не симметричная. Так как просматривается сходу пара знаков, то в цикле будет m = n div 2 повторений. Для запоминания результата просмотра введем переменную k (k будет равна 0, в случае, если строчок симметрична и 1 в противном случае).
Программа, решающая эту задачу, будет иметь вид:
var s:string;i,k,n,m:integer;begin readln(s); n:=length(s); k:=0; m:=n div 2; for i:=1 to m do if s[i]s[n-i+1] then k:=1; if k=0 then writeln(‘Строчок симметрична’) else writeln(‘Строчок несимметрична’);end.
Задача 3.2
В случае, если удалить из заданной строчка все пробелы, то задача сведется к прошлой.
Задача 3.3
Так как все цифры от 0 до 9 находятся в таблице кодировки компьютера подряд, то несложнее всего проверить, есть ли знак s[i] цифрой, возможно посредством неравенства ‘0’=’0′)and(s[i]
Задача 3.4
Пускай s — строчок. Обозначим длину строчка — l. Организуем цикл, в котором будем контролировать, есть ли очередной знак цифрой, в случае, если да, то организуем новый цикл, в котором будем вырабатывать строчок sn, складывающуюся из цифр (очередное целое число). Позже преобразуем sn в число и вычислим произведение. Программа на Паскале, реализующая этот метод, будет иметь следующий вид (переменная p в данной программе употребляется для накапливания значения произведения, переменная kod — для хранения кода результата преобразования строчка в число):
var sn,s:string; l,k,kod:integer; v,p:real;begin writeln(‘Введите строчок’); readln(s); l:=length(s); p:=1; k:=1; repeat sn:=»; while (s[k]=’0′)and(s[k]l; writeln(‘ p=’,p);end.
Задача 3.8
Обозначим s — исходную строчок, l — длину данной строки. Для решения создадим ещё одну строчок s1(сначала пустую). Потом организуем цикл по номеру знака в строчке s. В случае, если очередной знак не #, то добавим его к строчку s1, в случае, если это строка # и знак s1 не безлюдная, то удалим из неё последний знак.
Программа, реализующая этот метод, будет иметь следующий вид:
var s,s1:string; dl,i,k:integer;begin writeln(‘Введите строчок’); readln(s); dl:=length(s); s1:=»; k:=0; for i:=1 to dl do if (s[i]=’#’)and(k0) then begin delete(s1,k,1); k:=k-1; end else begin k:=k+1; s1:=s1+s[i]; end; writeln(s1);end.
Задача 3.10
Пускай s — заданная строчок. Для решения данной задачи определим длину строчка l и организуем цикл по номеру знака i. Знак строчка есть первым знаком некоего слова в том случае, в то время, когда он сам не есть пробелом, и или он — первый знак строчка, или слева от него стоит пробел. В случае, если мы нашли первый знак некоего слова, то запомним его номер и организуем цикл, в котором отыщем номер последнего знака этого слова (знак будет последним в слове или тогда, в то время, когда по окончании него стоит пробел, или в то время, когда он последний знак строчка). В случае, если последний знак слова сходится с первым знаком этого слова, и протяженность слова громаднейшая из всех отысканных, запомним номер и эту длину первого знака этого слова.
В приведенной программе введены следующие обозначения:
max — переменная, в которой запоминается текущая большая протяженность отысканного слова; k — переменная, в которой поочередно запоминается номер первого знака каждого слова; koord — переменная, в которой хранится номер первого знака слова с большой длиной.
var s:string; koord,k,i,n,max:integer; fst:char;begin writeln(‘Введите строчок’); readln(s); n:=length(s); max:=0; i:=1; while imax) then begin koord:=k; max:=i-k+1; i:=i+1; end; end else i:=i+1; if max0 then begin writeln(‘ max=’,max); for i:=0 to max-1 do write(s[koord+i]); end else writeln(‘Для того чтобы слова нет’) end.
Задача 3.11
Обозначим K — число левых скобок, M — число правых скобок, тогда, на каждом шаге подсчета скобок, должно выполняться условие: K=M. По окончании подсчета всех скобок должно выполниться условие K=M.
Задача 3.14
Имеется пара дорог ответа данной задачи. Для упрощения предположим, что строчок не начинается и не заканчивается пробелом и что между словами в строчке стоит ровно по одному пробелу. Пускай известна пара слов, которую нужно переставить, и — номера первой и последней букв в первом слове, и — номера первой и последней букв во втором слове. Разглядим метод, в котором для перестановки слов будем применять следующий метод:
Запишем буквы первого слова в обратном порядке (поменяв первую с последней, вторую с предпоследней и т.д.).
К примеру, из строчка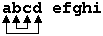 
возьмём dcba efghi.
Позже подобным образом переставим буквы второго слова:
из строчка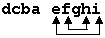 
возьмём dcba ihgfe.
Для получения окончательного результата нужно записать буквы взятого словосочетания в обратном порядке:
Из строки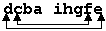 
возьмём efghi abcd (что и требовалось взять).
Так, для перестановки двух слов достаточно написать подпрограмму, которая меняет в заданной строчке порядок букв на противоположный (инвертирует строчок), и привести к этой подпрограмме для первого слова, второго слова и всего словосочетания.
Обозначим invert(k,l) — процедуру, которая записывает в заданной строчке s знаки с k-того по l-й в обратном порядке, тогда программа, решающая задачу, будет иметь вид:
var s:string; i,n,m1,m2,l1,l2:byte;procedure invert(k,l:byte);var i:byte; ch:char;begin for i:=k to ((l+k) div 2) do begin ch:=s[i]; s[i]:=s[l+k-i]; s[l+k-i]:=ch; end;end;beginwriteln(‘Введите строчок’); readln(s);i:=0; n:=0;m1:=1;m2:=1;l1:=1;l2:=1;while iЗадачи повышенной сложности
Задача 4.1
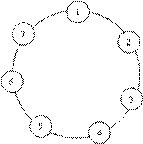В круге стоят N человек (рис.). Они пронумерованы от 1 до N. Поочередно из круга начинает выходить каждый третий человек. Это длится , пока в круге не останется последний человек. Выяснить его номер.
К примеру, в случае, если в круге стояло 7 человек, то его поочерёдно покинут 3, 6, 2, 7, 5, 1. Оставшимся будет человек, находившийся на 4 месте.
Задача 4.2
Вывести на экран цифры числа 31000. В случае, если постараться взять число конкретно умножением, компьютер выдаст сообщение об неточности.
Задача 4.3
Разработать программу для умножения двух чисел, количество цифр в каждом из которых может быть около 100. К примеру, для умножения вида:
9278969345897569872365*5705782370079678659.
Задача 4.4
Сообщество роботов живет по следующим законам: один раз в год они объединяются в абсолютно укомплектованные группы по 3 либо 5 роботов (причем число групп из 3 роботов — максимальное). За год группа из 3 роботов собирает 5, а группа из 5 — 9 новых собратьев. Любой робот живет 3 года по окончании сборки. Известно начальное количество роботов (К7), все они только что собраны. Выяснить какое количество роботов будет через N лет.
Задача 4.5
На квадратном клетчатом листе бумаги 8×8 клеток заштрихована часть клеток (пример на рисунке). Выяснить вписанный в решётку прямоугольник большой площади, не содержащий заштрихованных клеток. В качестве ответа вывести координаты и площадь прямоугольника его двух противоположных вершин. (Предполагается, что прямоугольник с большой площадью один.)
Для приведенного примера координаты вершин (3,4) и (7,6), площадь 15 клеток.
Задача 4.6
На квадратном клетчатом листе бумаги n на m клеток нарисовано пара фигур, любая из которых состоит лишь из целых клеток. Разные фигуры не накладываются и не соприкасаются (пример на рисунке). Выяснить фигуру большой площади. (В качестве ответа вывести координаты и площадь фигуры одной из её точек. Предполагается, что фигура с большой площадью одна.)
К примеру, на странице 8 на 8 клеток:
Площадь фигуры равна 6. Координаты одной из её клеток (2,3).
Задача 4.7
Подсчитайте количество одно-, двух-, трёх- и четырехпалубных судов, расположенных на поле для игры Морской бой. Суда не смогут быть изогнутыми и между собой не соприкасаются. Поле для игры задается в виде таблицы 10×10, любой элемент которой равен или 0, в случае, если клетка свободна, или 1, в случае, если занята.
Задача 4.8
Лабиринт задан в виде матрицы размером n на m. Стенкам лабиринта соответствуют единицы, проходам — нули. Выяснить, возможно ли из точки с координатами (i1, j1) попасть в точку с координатами (i2, j2). Для усложнения задачи возможно предложить указать самый маленький путь из заданной точки, причем из всех дорог однообразной длины выбирать путь с мельчайшим числом поворотов.
Задача 4.9
На рисунке изображен треугольник из чисел. Вычислите солиднейшую сумму чисел, расположенных на пути, начинающемся в верхней точке треугольника и заканчивающемся на его основании. Любой ход на пути может идти вниз по диагонали влево либо вниз по диагонали вправо. Число строчков в треугольнике больше1 и не больше100. Треугольник составлен из целых чисел от 0 до 99.
Задача 4.10
Имеется n населенных пунктов, пронумерованных от 1 до n. Кое-какие пары пунктов соединены дорогами (а также дорогами с односторонним перемещением). Выяснить, возможно ли попасть по этим дорогам из одного заданного пункта в второй. (Для усложнения задачи возможно предложить указать все вероятные дороги без петель и тупиков из одного пункта в второй).
Задача 4.11
Заданы две фразы. Выяснить громаднейшую последовательность хороших от пробелов знаков, входящую в обе фразы в одном и том же порядке. К примеру, в предложениях:
ПРИШЛА ВЕСНА и РАСТАЯЛ СНЕГ такая последовательность — Р,А,С,Н.
Задача 4.12
В морском порту города Владивостока сохраняются N контейнеров (N — чётное число). Для погрузки контейнеров на судно, дабы обеспечить равномерную загрузку, их нужно поделить на две половины так, дабы их веса были максимально близки. Решить эту задачу, предполагая, что информация о весах контейнеров (в тоннах) хранится в массиве M(N). В качестве ответа указать номера контейнеров одной половины и приобретаемые веса для каждой из половин.
К примеру:
В случае, если M(6)=(10, 15, 18, 20, 16, 14), то одну половину составят 1, 4, 5 контейнеры (другую 2, 3, 6). Масса первой группы m1=10+20+16=46 т., масса второй группы m2=15+18+14=47 т.
Задача 4.13
На шахматной доске нужно расставить 8 ферзей так, дабы они не угрожали друг другу.
Задача 4.14
На шахматной доске размером 4×4 клетки расставить 4 ладьи так, дабы они не угрожали друг другу. Выяснить все такие расстановки (всего их будет 24).
Решения задач
Задача 4.2
Для записи солидных чисел комфортно применять массивы, записывая цифры числа как элементы массива. Оценим количество цифр, нужных для записи 31000:
32 = 9; 31000 = (32)500 = 9500 10500.
Так, в записи этого числа будет менее 500 цифр.
Запишем сначала в массив лишь число 3 и потом будем умножать его поэлементно на 3 необходимое число раз, учитывая перенос из разряда в разряд, появляющийся при умножении.
Программа, решающая эту задачу, возможно записана, к примеру, так:
какое количество stp=1000;var i,j,k,prn,x:integer; a:array [1..500] of integer;begin a[500]:=3; prn:=0; for i:=2 to stp do for j:=500 downto 1 do begin x:=a[j]*3; a[j]:=(x+prn) mod 10; prn:=(x+prn) div 10; end; k:=1; while (a[k]=0) do k:=k+1; for i:=k to 500 do write(a[i]:1); writeln
end.
Тут stp — степень, в которую возводится число 3, a[500] — массив, в котором сохраняются цифры взятого числа, prn — перенос из разряда в разряд. Количество вычислений в данной программе возможно существенно сократить, в случае, если любой раз умножать на 3 отнюдь не весь массив a, а лишь его занятую часть.
Задача 4.3
Принцип ответа данной задачи такой же, как и у предыдущей. Итог умножения двух стозначных чисел будет не быть больше по размеру 200 знаков (т.е. для хранения результата пригодится массив из 200 элементов). Для ввода исходных чисел комфортно применять строковый тип данных.
Задача 4.4
Разглядим следующий вариант ответа. Создадим массив R(3), где R1, R2, R3 — количество роботов соответствующего возраста. Тогда общее число роботов S= R1+ R2+ R3. Обозначим x — количество троек, y — количество пятерок, которое возможно организовать из общего количества роботов (мысль разбиения на пятёрки и тройки рассмотрена в задаче 1.5). Ежегодно роботы стареют, общее число роботов возрастает на 5x+9y и значительно уменьшается на R3 (число роботов, проживших 3 года). Программа ответа возможно записана так:
var k,i,n,p:integer; s,x,y:longint; r:array [1..3] of longint;begin write(‘Начальное количество роботов k=’); readln(k); write(‘Число лет n=’); readln(n); r[1]:=k; r[2]:=0; r[3]:=0; s:=k; for i:=1 to n do begin x:=s div 3; p:=s mod 3; if p=0 then y:=0 else if p=1 then begin x:=x-3; y:=2 end else begin x:=x-1; y:=1 end; r[3]:=r[2]; r[2]:=r[1]; r[1]:=5*x+9*y; s:=r[1]+r[2]+r[3]; end; writeln(‘s=’,s)end.
В данной программе употреблялся тип longint, предназначенный для хранения солидных целых чисел (до 2147483647). Это связано с тем, что неспециализированное число роботов возрастает весьма скоро. Так, к примеру, в случае, если начальное число роботов — 10, то через десятилетие их будет 143702.
Задача 4.5
Представим лист бумаги в виде числовой матрицы А(8×8). Обозначим заштрихованные клетки единицами, а чистые — нулями.
Данную программу комфортно реализовать, применяя подпрограммы. Напишем подпрограмму, которая контролирует, имеется ли в прямоугольнике с координатами левой верхней вершины (i1,j1) и координатами правой нижней вершины (i2,j2) заштрихованные клетки (т.е. элементы, равные 1).
function prov(a:matr;i1,j1,i2,j2:integer):boolean;var i,j:integer;begin prov:=true; for i:=i1 to i2 do for j:=j1 to j2 do if a[i,j]=1 then prov:=false;end;
Эта функция будет возвращать значение истина (true), в случае, если заштрихованных клеток в разглядываемом прямоугольнике нет, и ложно (false) — в другом случае.
В главной программе организуем два попарно положенных цикла: в первом цикле будут изменяться координаты верхнего левого угла разглядываемого прямоугольника, во втором — координаты нижнего правого угла. В случае, если в прямоугольнике нет заштрихованных точек, то вычислим его площадь, и если она есть большой, запомним её и координаты противоположных вершин этого прямоугольника. Часть главной программы, реализующая этот метод, будет иметь следующий вид:
maxs:=0; for i1:=1 to n do for j1:=1 to n do for i2:=i1 to n do for j2:=j1 to n do begin s:=(i2-i1+1)*(j2-j1+1); if prov(a,i1,j1,i2,j2)and(maxsЗдесь maxs — площадь взятого прямоугольника, (maxi1, maxj1) — координаты его левой верхней вершины, (maxi2, maxj2) — координаты его правой нижней вершины.
Задача 4.6
Подобные задачи достаточно с применением рекурсии. Ответ выстроим следующим образом: представим лист в виде числовой матрицы А(nxm). Обозначим заштрихованные клетки единицами, а чистые — нулями. Напишем рекурсивную процедуру, которая определяет площадь заштрихованной фигуры и заменяет клетки уже просмотренной фигуры двойками (дабы не просматривать эту фигуру ещё раз). В главной программе организуем цикл перебора всех элементов матрицы. В случае, если очередной элемент равен 1 (ещё не просмотренная фигура), то будем приводить к процедуре определения площади данной фигуры).
Процедура рекурсивного определения площади фигуры будет иметь вид:
procedure zaliv(i,j:byte; var s:integer);begin a[i,j]:=2; s:=s+1; if (i+10)and(a[i-1,j]=1) then zaliv(i-1,j,s);end;
Тут n и m — число строк и столбцов в разглядываемой матрице, i, j — координаты отысканной клетки фигуры, s — переменная, в которой накапливается площадь фигуры. Процедура учитывает отысканную клетку в площади, позже контролирует, заштрихована ли клетка, которая расположена ниже просматриваемой (в случае, если это не последняя строчок), и в случае, если да, то рекурсивно вызывается с данной клетки, позже тот же процесс повторяется для клеток расположенных справа, слева и сверху от разглядываемой. Рабочая часть главной программы будет иметь вид:
max:=0; im:=0; jm:=0;for i:=1 to n dofor j:=1 to m do if a[i,j]=1 then begin s:=0; zaliv(i,j,s); if smax then begin max:=s; im:=i; jm:=j; end; end;writeln(‘Smax=’,max,’ im=’,im,’ jm=’,jm);
Тут max — переменная, в которой хранится большая площадь фигуры, im, jm — координаты первой отысканной точки данной фигуры.
Задача 4.8
самый простым методом ответа задач по поиску пути есть рекурсивный поиск. Его метод во многом подобен рассмотренному в задаче 4.6.
Пускай A(nxm) — матрица, задающая лабиринт (1 — стенки, 0 — проход). Напишем процедуру рекурсивного перемещения по лабиринту. Путь прохода будем отмечать цифрами, начиная с 2 (2, 3, 4 и т.д.). Пускай на k-том шаге мы попали на клетку с координатами (i, j). В случае, если это та клетка, путь до которой нужно было найти (с координатами (i2, j2)), то задача решена. Нужно распечатать матрицу с отмеченным методом и завершить исполнение программы. В случае, если нет, то нужно проверить, возможно ли перейти на соседнюю клетку (справа, слева, сверху либо снизу), и в случае, если быть может, то привести к процедуре перемещения уже с данной клетки. В случае, если перехода на соседнюю клетку нет, то нужно очистить исходную клетку, дабы её возможно было применять в других вариантах при поиске пути. Обозначим move(i,j,k) — процедуру рекурсивного перемещения (i, j — номер клетки, k — номер шага), writematr — процедуру, распечатывающую матрицу A, тогда программа, реализующая предложенный метод, возможно записана следующим образом:
const n=4; m=5;type matr=array [1..n,1..m] of integer;{Матрица, задающая варианты прохода. 1-стенки; 0-проход.}const labir:matr=((1,0,0,0,1), (0,0,1,0,1), (1,0,0,0,0), (0,0,1,0,0));var a:matr; i1,j1,i2,j2,f:byte; k:integer;procedure writematr;var i,j:byte;beginfor i:=1 to n do begin for j:=1 to m do write(a[i,j]:3,’ ‘); writeln; endend;procedure move(i,j:byte; k:integer);begin a[i,j]:=k; k:=k+1; if (i=i2)and(j=j2) then begin writematr; f:=1; halt end else begin if (i+10)and(a[i-1,j]=0) then move(i-1,j,k); end; a[i,j]:=0; k:=k-1;end;begin a:=labir; writeln(‘Координаты i1, j1’); readln(i1,j1); writeln(‘Координаты i2, j2’); readln(i2,j2); f:=0; k:=2; if(a[i1,j1]=1)or(a[i2,j2]=1) then writeln (‘Неверные координаты’) else move(i1,j1,k); if f=0 then writeln(‘Прохода нет’);end.
Тут — labir — матрица-константа 4×5, задающая пример лабиринта, f — переменная, через которую отслеживается, имеется ли проход из начальной точки в конечную либо нет, процедура halt — стандартная процедура, которая прекращает исполнение программы.
В случае, если забрать в качестве начальной точки точку с координатами (4, 1), в качестве конечной — точку с координатами (1, 4), то рассмотренная программа выдаст следующий вариант прохода:
1 0 0 8 1
0 0 1 7 1
1 4 5 6 0
2 3 1 0 0
Задача 4.11
Для решения данной задачи разглядим стандартную задачу перебора всех вероятных сочетаний элементов некоего массива. Пускай X(n) — массив с элементами 1, 2, … n (массив номеров). Разработаем программу, которая на базе этого массива генерирует все подмножества номеров, складывающиеся из m элементов.
К примеру, при n=5, m=3. X(5)=(1,2,3,4,5)
Подмножества из 3-х номеров: (1,2,3), (1,2,4), (1,2,5), (1,3,4), (1,3,5), (1,4,5), (2,3,4), (2,3,5), (2,4,5), (3,4,5). Порядок перебора, рассмотренный в примере, именуется лексикографическим. Таковой порядок подобен размещению слов в словаре: сперва сравниваются первые буквы, позже вторые и т.д. Всего сочетаний из n элементов по m будет (см. задачу 2.3), другими словами .
Для упрощения структуры программы напишем процедуру, которая печатает первые m элементов массива X(n) (предположим, что массив обрисован глобально):
procedure printm(m:integer);var i:integer;begin for i:=1 to m do write(x[i],’ ‘); writeln;end;
Потом разглядим функцию, которая на базе очередного сочетания приобретает следующее по порядку сочетание:
function posl(m:integer):boolean;var j,f:integer;label 10,20;begin f:=0; posl:=true; for j:=m downto 1 do if x[j]=n+j-m then f:=j else begin inc(x[j]); goto 10 end;10: if f0 then if f=1 then begin posl:=false; goto 20 end else for j:=f to m do x[j]:=x[f-1]+j-f+1;20:end;
Эта функция возвращает значение истина (true), в случае, если переданное сочетание не последнее (для рассмотренного примера: (1,3,4) либо (2,4,5)), и значение неправда (false), в случае, если переданное в функцию сочетание последнее (для рассмотренного примера — (3,4,5)). Функция применяет лишь первые m элементов массива X(n). В первом цикле проверяется, возможно ли расширить какой-либо из элементов массива (начиная с последнего). В случае, если возможно расширить последний (m-й) элемент, то он возрастает, служебной переменной f присваивается значение 0, и происходит выход из функции (к примеру, из последовательности (1,2,4) получается последовательность (1,2,5)). В случае, если последний элемент уже нельзя увеличить (к примеру, последовательность (1,4,5)), то находится элемент, что еще возможно расширить (в этом случае 1), данный элемент возрастает, а во втором цикле за ним выстраиваются остальные (так, из (1,4,5) возьмём (2,3,4)). В этом случае в f сохраняется номер элемента, следующего за увеличенным.
Программа, печатающая все сочетания из n элементов по m (при n=5, m=3), будет иметь вид:
const n=5;var x:array[1..n] of integer; m,j:integer;…{Описание процедур printm и posl}…beginm:=3;for j:=1 to m do x[j]:=j;repeat printm(m);until not posl(m);end.
Удобство написанной функции в том, что, для получения всех вероятных сочетаний из n номеров достаточно добавить в главную часть программы цикл по m:
begin for m:=n downto 1 do begin for j:=1 to m do x[j]:=j; repeat printm(m); until not posl(m); end;end.
Для решения главной задачи нужно удалить из обеих строчков пробелы, потом выбирать в порядке убывания длины сочетания из букв одной строки и контролировать, входят ли они в другую (в случае, если да, то ответ отыскано). Программа, решающая задачу, будет иметь вид:
const k=255;var x: array [1..k] of integer; m,n,j: integer; s1,s2,s: string;label 1;…{Описание процедуры posl}…procedure prints(m:integer);var i:integer;begin write(m,’: ‘); for i:=1 to m do write(s1[x[i]]); writeln; readln;end;function spc(s:string):string;var str:string; i:integer;begin str:=»; for i:=1 to length(s) do if s[i]’ ‘ then str:=str+s[i]; spc:=str;end;function equal(m:integer):boolean;var i,j:integer;begin j:=1; for i:=1 to length(s2) do if (s1[x[j]]=s2[i])and(jm then equal:=true else equal:=false;end;begin writeln(‘Введите первую строчок’); readln(s1); writeln(‘Введите вторую строчок’); readln(s2); s1:=spc(s1); s2:=spc(s2); if (length(s2)В данной программе процедура prints печатает отысканную последовательность знаков и её длину, функция equal контролирует, входит ли очередная последовательность, составленная из знаков одной строки в другую, функция spc удаляет из переданной в неё строчка пробелы.
Работу взятой программы возможно существенно ускорить, в случае, если добавить в неё часть, в которой перед перебором из обеих строчков удалялись бы те знаки, каковые видятся лишь в одной из них. (К примеру, заданные в условии строчка по окончании для того чтобы преобразования приняли бы вид: РЛАЕСНА и РАСАЛСНЕ).
Задача 4.13
Эта задача решена во многих книгах по программированию (к примеру, в [4,5]). Так как ферзей 8, то разумеется, что на горизонтали и каждой вертикали будет находиться по одному ферзю, исходя из этого можно считать, что ферзь с номером k стоит на k-той вертикали и нужно отыскать его координату по горизонтали.
Задача 4.14
Как и в прошлой задаче, будем вычислять, что на каждой вертикали стоит по ладье, и для каждой из них нужно отыскать координату по горизонтали (причем не совпадающую с соответствующими координатами остальных ладей). Так, исходная задача сводится к нахождению всех вероятных перестановок из 4 элементов. Как мы знаем, что число перестановок из n элементов равняется n!=1*2*3*…*n. К примеру, из 3 элементов возможно взять 3!= 1*2*3=6 перестановок:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
Так как методы перестановок довольно часто употребляются в олимпиадных задачах, разглядим их подробнее. самый коротким и несложным для запоминания есть рекурсивный метод получения перестановок. Пускай X[n] — массив, элементы которого числа от 1 до n. Для упрощения программы будем применять процедуру printm, печатающую массив X, и процедуру swap(a,b), меняющую местами значения переменных a и b. Тогда программа рекурсивного получения перестановок (при n=4) будет иметь вид:
const n=4;var x:array [1..n] of integer; i:integer; procedure printm;var i:integer;begin for i:=1 to n do write(x[i],’ ‘); writeln;end;procedure swap(var a,b:integer);var v:integer;begin v:=a; a:=b; b:=vend;procedure perest(k:integer);var i:integer;begin if k=n-1 then printm else for i:=k+1 to n do begin swap(x[k+1],x[i]); perest(k+1); swap(x[k+1],x[i]); end;end;begin for i:=1 to n do x[i]:=i; perest(0);end.
Эта программа трудится по следующему принципу: первоначально процедура perest будет рекурсивно вызываться до тех пор, пока не будет распечатан исходный массив X (без перестановки элементов):
1 2 3 4
Позже случится отход на ход назад, перестановка двух последних элементов, и при очередном вызове печать оказавшегося массива:
1 2 4 3
по окончании чего массив вернётся в круги своя.
Позже случится еще один отход назад и перестановка последнего и третьего с конца элементов, по окончании чего процедура будет опять рекурсивно вызываться, пока не будет распечатан массив X:
1 4 3 2
Потом снова будут переставлены два последних элемента:
1 4 2 3
и т.д. Особенность данного метода в том, что по окончании окончания он оставляет исходный массив X без трансформаций. Из программ, каковые не применяют рекурсию, разглядим следующую:
const n=4;label 10,20,30;var x,c:array[1..n] of integer; i,j:integer;…{описание процедур swap и printm}…begin for i:=1 to n do x[i]:=i; printm; for i:=2 to n do c[i]:=1; 20: for i:=2 to n do begin if c[i]i then goto 10; for j:=2 to i do c[j]:=1; end; goto 30; 10: for j:=1 to trunc(i/2) do swap(x[j],x[i+1-j]); printm; c[i]:=c[i]+1; goto 20; 30:end.
Массив X(n) в данной программе — массив номеров, массив C(n) — служебный массив, что употребляется для отслеживания числа сделанных перестановок.