КОМБИНАТОРНЫЕ ЗАДАЧИ
Цели:1. Дать первые понятия перестановкам, размещениям, сочетаниям с повторением и без повторения.
2. Научить правилам полного перебора.
3. Научить решать задачи на разную комбинацию чисел.
Задачи для подготовки
В деревне Простоквашино на скамье перед домом сидят дядя Федор, кот Матроскин, пес Шарик, почтальон Печкин. В случае, если Шарик, сидящий крайним слева, сядет между Матроскиным и дядей Федором, то Федор окажется крайним слева. Кто где сидит?
Задачи на перестановку
1. Крокодил Гена решил позвонить Чебурашке по телефону, но внезапно понял, что забыл номер телефона. Гена отлично не забывает, что первые цифры 5 и 2. А остальные он не забывает, но забыл порядок. Это цифры: 1, 3, 4, 6. Какое самое много раз придется Гене собрать номер?
ОТВЕТ:
4-6
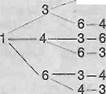6 раз, в случае, если начать с цифры 1, аесли с вторых цифр, то 4 х 6 = 24 раза.
2. какое количество разных костюмов возможно составить из штанов и двух рубах, в случае, если костюм обязан складываться из штанов и одной рубахи?
3. От Бабы-Яги до Кащея ведет одна дорога, а от Кащея до Кикиморы — две дороги (см. рис.). какое количество методами возможно дойти от Бабы-Яги до Кикиморы, в случае, если нужно зайти к Кащею? Похожи ли задачи 2 и 3?
Кащей
| Баба-Яга |
Кикимора
4. От Марининого дома до Сашиного возможно проехать на велосипеде по двум дорогам (двумя методами), а от Сашиного дома до Лизиного — тремя методами (см. рис.). какое количество методами возможно доехать на велосипеде от Марины до Лизы, в случае, если по дороге нужно заехать к Саше?
5. Карлсон съел яблоко, персик и грушу. В каком порядке он м0г их съесть, в случае, если любой фрукт Карлсон ел раздельно? Перечисли все методы.
6. какое количество всего двузначных чисел возможно составить из цифр 1. 2. 3 при условии, что цифры в записи каждого числа не повторяются? Перечисли все эти числа и отыщи их сумму.
7. какое количество трехзначных чисел возможно составить из трех разных не равных нулю цифр? Зависит ли итог о того, какие конкретно конкретно цифры мы берем? Укажи какой-нибудь метод перебора трехзначных чисел, при котором ни одно число не может быть пропущено. Изменится ли число вариантов, в случае, если одна цифра — ноль?
8′. какое количество методами возможно переставить 3 разные буквы, 3 разные цифры, трех человек в последовательности, 3 книжки на полке? А какое количество методами возможно переставить 4 разных предмета? (А, В, С, Д).
9. какое количество дорог.
Из деревни Аленкино в деревню Борискино ведут 3 дороги. Из Борискина в Ваняткино — 4. А из Ваняткина в Галинкино — 5 дорог. какое количество методами возможно попасть в деревню Галинкино, шагая через Борискино и Ваняткино?
3-1=3 3-4=12 12 • 5 = 60 (способов)
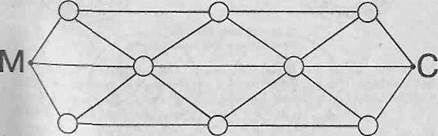
10. Мамонтёнок в отыскивании мамы отправился в Африку. какое количество различными методами он может выбрать себе маршрут, плывя от островка к островку?
12. Белоснежка, Дюймовочка, Мальвина, Красная Золушка и Шапочка перед Новым годом решили поздравить по телефону ДРУГ друга с праздником. Причем, любая сказочная героиня переговорила по телефону с каждой из собственных подруг. какое количество всего было телефонных звонков?
Замечание: в случае, если Мальвина позвонила и поздравила Золушку, то будет ли Золушка звонить Мальвине?
13. В шахматном турнире приняли участие 7 человек. Любой с каждым сыграл по одной партии. какое количество партий они сыграли?
ОТВЕТ: 1 метод. Любой шахматист сыграл 6 партий. Всего сыграна 21 партия (произведение 7×6 необходимо поделить на два, в другом случае любая партия будет сосчитана два раза).
2 метод, (посредством графов). Пускай любой шахматист обозначен точкой, а любая сыгранная партия стрелкой от одного шахматиста к второму. (На рисунке обозначены партии лишь для первых двух игроков). В случае, если каждую партию вычислять один раз, то будем иметь 21 партию (6 + 5 + 4 + 3 + 2 + 1 = 21).
14. Семь человек обменялись фотографиями. какое количество наряду с этим было роздано фотографий?
Ответ. Т.к. любой из семи человек дал 6 фотографий (всем, не считая себя), то всего было роздано 42 фотографии
ПРИНЦИП ДИРИХЛЕ» (выбор предметов в темноте)
Цель: 1. Научить делать выбор по лучшему и .нехорошему случаю.
2. Научить использовать этот метод при ответе задач на подтверждение.
Задачи на подтверждение
1 В одном доме живут 13 учеников одной школы. В школе 12 классов. Доказать, что хотя бы 2 ученика, живущие в этом доме, получают образование одном классе.
2, В классе 40 учеников. Найдется ли таковой месяц в году,
в котором отмечают собственный сутки рождения не меньше, чем 4 уче
ника класса?
Ответ: Да. 40 : 13 = 3 (4 ост.). .
3. В спортивной секции 35 мальчиков. Возможно ли утверждать,
что среди них найдется хотя бы два спортсмена, фамилии
которых начинаются с одной буквы?
Ответ: Да.
ЗАДАЧИ «ТУДА-ОБРАТНО»
В двух аквариумах плавают рыбки. В случае, если из первого аквариума пересадить одну рыбку во второй аквариум, то рыбок в аквариумах будет поровну. А вдруг из второго аквариума пересадить одну рыбку в первоначальный, то в первом будет рыбок в 2 раза больше, чем во втором. какое количество рыбок в каждом аквариуме?
ОТВЕТ: 1 + 1 =2(рыб.), 2 + 2 = 4 (рыб.). 2 части — 1 часть = 1 часть 4 рыб. —1 часть 2 части —8 рыб 8-1=7 (рыб), 4 + 1=5 (рыб). Ответ: 5 и 7.
2. В случае, если Петя даст Саше 100 рублей, то у друзей денег будет поровну, а вдруг Саша даст Пете 100 рублей, то у Пети будет Денег в 9 раза больше, чем у Саши. какое количество денег у каждого? ОТВЕТ: 100 руб.+ 100 руб. =200 руб. 200 руб.+ 200 руб. = 400 руб. 9 ч.-1 ч. = 8 ч., 400 руб. : 8 = 50 руб. 50 руб.+ 100 руб. = 150 руб. 150 руб.+ 200 = 350 руб.
Ответ: 150 и 350.
3. Как возможно поделить 45 на 4 части так, что в случае, если к первой
части прибавить 2, от второй забрать 2, третью умножить на
2 и четвертую поделить на 2, то окажутся однообразные числа?
ОТВЕТ: Примем третье число за одну часть, тогда четвертое число равняется 4 частям, а второе и первое, каждое в отдельности,—двум частям, в случае, если к одному из них прибавить 2, а от второй забрать 2.
Всего частей: 2 + 2 + 1+4 = 9. Третье число равняется 45 : 9 = 5, четвертое —20, второе: 5 • 2 — 2 = 8 и первое 5 • 2 + 2 = 12.
Ответ. 8, 12, 5, 20.
4. Ваня говорит Пете: «Будь у меня на 4 яблока больше, чем
у меня имеется сейчас, то у меня было бы в два раза больше, чем у тебя. какое количество яблок у каждого, в случае, если у обоих совместно 26 яблок?
Схема оказывает помощь строить рассуждения и отражает содержание задачи.
В случае, если добавить Ване 4 яблока, то у них будет 3 части = 30 яблокам, 1 часть —10 яблок (у Пети). Следовательно, у Вани —16 яблок.
Рассуждая так же, реши задачи.
5. У двоих мальчиков было совместно 10 груш. В то время, когда один мальчик съел одну грушу, а второй —3 груши, у них осталось груш поровну. какое количество груш было у каждого?
6. На двух тарелках лежало 9 яиц. В то время, когда с одной тарелки забрали яйцо, то на данной тарелке осталось яиц в 3 раза больше, чем на другой. какое количество яиц было на каждой тарелке?
7. У моего брата было в 3 раза больше орехов, чем у меня. В случае, если же он съест 6 орехов.то у нас будет орехов поровну. какое количество орехов у каждого из нас?
Продолжи ответ, обозначив на схеме 6 орехов.
8. У одного мальчика было тетрадей в два раза больше, чем у другого. В то время, когда он приобрел еще 6 тетрадей, то у него осталось тетрадей в 5 раза больше. какое количество тетрадей было у каждого?
9. Три рыболова дали согласие всю выловленную рыбу дробить поровну один поймал 12 штук, второй —7 штук, а третий —8штук. Кто из них какое количество обязан дать?
10. У юннатов было 20 гусей и штук уток. В то время, когда 4 уток и 6 гуся
отдали в колхоз, у них гусей и уток осталось поровну. какое количество
гусей и уток было у юннатов в отдельности?
11. Полсотни яблок разложили в одну громадную и две ма
ленькие корзины. В громадную корзину положили на 8 яблок
больше, чем в каждую мелкую корзину. какое количество яблок
в каждой корзине?
МЕТОД «ЛИШНИЙ ЯЩИК»
1. По тропинке на протяжении кустов шло 11 хвостов. Насчитать я так же смог, что шагало 30 ног. Это совместно шли куда-то жеребята и индюки, а сейчас вопрос таков: какое количество было индюков? Спросим так же у ребят: какое количество было жеребят?
ОТВЕТ:
1 МЕТОД
1) Допустим 11 животных —все индюки.
а) 11 • 2 = 22 (ноги) у 11 индюков.
Должно быть 30 ног. На какое количество ног выяснилось меньше?
б) 30-22 = 8
у каждого жеребенка на 2 ноги больше, чем у индюка.
в) 8: 2 = 4 (жеребят)
г) 11-4 = 7 (индюков)
Ответ: 7 жеребёнка и 4 индюков.
2) Возможно высказать предположение, что все животные —жеребята.
а) 11 • 4 = 44 ноги
На какое количество оказались больше?
6)44-30 = 14
Любой жеребенок —это 2 лишних ноги.
в) 14 : 2 = 7 (индюков) —
Значит 7 индюков.
г) 11—7 = 4 (жеребят)
Ответ: 7 жеребят и 4 индюков.
II. МЕТОД, предположения с перебором (либо подбором)
Предположим, что индюк 1, тогда у него ног—2, а ног—10 и жеребят у них —40, 40 + 2 = 42 (ноги), а должно быть 30. Рассуждая так же, составляем таблицу:
| всего ног | ||||||
| инд. (2 н.) | (1) 2 | (2) 4 | (3) 6 | (4) 8 | (7)14 | |
| жер. (4 н.) | — (10) 40 | (9) 36 | (8)32 | (7)28 | (4) 16 | |
Возможно выбирать до верного ответа, а возможно, увидев закономерность, пропустить пара переборов. 2. пауки и Жуки.
У меня в одной коробке имеется жуки, И еще в второй коробке —пауки. Мало их, в одну 60 секунд возможно съесть: Пауков с жуками совместно—лишь шесть. Начал считать я: в двух коробках какое количество ног? Весьма долго сосчитать я их не имел возможности. Право, кроме того зашумело в голове: Выяснилось, ног много —сорок две! Ну, сообщи сейчас мне, сколько тут жуков? И еще сочти раздельно пауков.
ЗАДАЧИ НА ВЗВЕШИВАНИЕ
Взвешивание монет. задачу возможно продолжить: 1) Как отмерить 1 л воды?
Во всех этих задачах предлагается некое число однообразных с виду монет. Одна либо пара из них отличаются по весу от остальных. Очевидно, разность в весе слишкоммала, дабы ее допустимо было найти, легко забрав монету руку. Исходя из этого мы предлагаем воспользоваться чашечными весами, каковые разрешают сравнивать вес разных монет. Но гирь у нас нет. Как же поступить, дабы выяснить самую тяжелую либо самую легкую монету?
Задача! Имеется 8 однообразных с виду монет. На каждую чашу весов кладут по четыре монеты. Одна чаша весов перевешивает, потому что одна из монет отличается по весу от остальных семи. Посредством какого именно числа дополнительных взвешиваний возможно найти монету, хорошую по весу от остальных?
Задача 2. Имеется 9 однообразных с виду монет, одна из которых легче по весу от остальных восьми. Как выяснить эту монету, пользуясь чашечными весами без гирь?
А вдруг нам не известно, легче либо тяжелее эта монета остальных, сколько потребуется взвешиваний?
|
3. весы и Бриллианты В коробке лежат 242 алмаза, из которых один природного происхождения, остальные его копии, изготовленные в лаборатории (неестественные). Массы неестественных бриллиантов однообразны, масса природного меньше. Придумайте совокупность действий для выделения природного алмаза при помощи 5 взвешиваний на чашечных весах без гирь.
ЗАДАЧИ НА ПЕРЕЛИВАНИЕ
1. Имеются две безлюдные банки в 5 л и 3 л и ведро с водой. Как посредством этих банок возможно отмерить 6 л воды? Эту задачу решают обучающиеся следующим образом:
1 переливание
2 переливание
3 переливание
После этого
| 5л | Ол | Зл | Зл | 5л |
| Зл | Зл | Ол | Зл | 1л |
2). Как отмерить 7 л воды?
| 2л |
| 5 л 2 л |
| Зл |
2 л 2 л
| О л 3 л |
(в ведро)
3) Как отмерить 4 л воды?
5л
Зл
Продолжи ответ
2) .Как отмерить 3 л воды, в случае, если имеется кружки 7 л и 2 л?
3. Чип и Дейл решили поделить, пополам молоко, которое
налито в 8-литровый кувшин. Еще нашлись безлюдные кувшины
в 5 литров и 3 литра.
4. Как посредством семилитрового ведра и трехлитровой
банки налить в кастрюлю 5 л воды?
5. Разлейте молоко
В вашем распоряжении имеются четыре емкости: 200 г, 400 г, 600 г, 800 г, —все цилиндрической формы.
Емкость, вмещающая 400 г, наполнена молоком, остальные—безлюдные. Пользуясь лишь этими емкостями, разлейте молоко так, дабы в каждой емкости цилиндра выяснилось ровно по 100 г.
6. Три сосуда заполнены (не доверху) водой. В одном сосуде
11 л, во втором —7 л, в третьем —6 л В любой сосуд возможно
налить из другого столько воды, сколько в нем было налито.
Как поделить воду во всех трех сосудах поровну?
ОТВЕТ.
Потому, что в трех сосудах 24 л, то в каждом сосуде должно быть 8 л. Задача сводится к получению трех чисел 8 посредством вычитания и сложения данных чисел и чисел, получающихся в следствии вычитания и сложения данных:
8 = (7+7)-6, 8 = (11-7)+4, 8 = (6 + 6)-4.
Процесс переливания возможно изобразить в виде таблицы:
7 В первоначальный сосуд входит 8 л, во второй —5 л, в третий —3 л.
пвый сосуд наполнен водой, а остальные два безлюдны. Как
«мощью этих сосудов отмерить 1 л воды? Как отмерить 4 л воды?
ОТВЕТ. 1 метод 2 метод
123. 123
800 800
503 350
530 323
| 5л |
233 620
251 602
701 152
701143
413
8. В один сосуд входит 3 л, в второй 5 л. Как посредством этих сосудов налить в кувшин 4 л воды из водопроводного крана? ОТВЕТ
Наполняем сосуд в 5 л и отливаем в трехлитровый сосуд. Оставшиеся 2 литра переливаем в кувшин. Повторяя эту операцию, нальем в кувшин 4 л воды.
ЗАДАЧИ, РЕШАЕМЫЕ С КОНЦА
24 конфеты поделили на три неравные кучки. В случае, если из первой кучки переложить во вторую столько конфет, сколько было в данной второй кучке, после этого из второй кучки переложить в третью столько, сколько было в данной третьей, и наконец, из третьей переложить в первую столько конфет, сколько в данной первой кучке осталось, то по окончании всех перекладываний число конфет во всех кучках будет одинаково. какое количество конфет было в каждой кучке первоначально?
ОТВЕТ:
По окончании всех перекладываний в каждой кучке стало по 8 конфет. Перед этим в 1 кучку было добавлено столько, сколько конфет в том месте имелось, другими словами их число удвоилось. А стало их 8. Следовательно, перед этим лежало 4, а 4 конфеты переложены из 3 кучки, исходя из этого до последнего перекладывания:
в 1 —4 конфеты,
во 2-8 конфет,
в 3-12 конфет.
Второй раз из второй кучки в третью переложили столько конфет, сколько в третьей имелось, значит 12-это удвоенное число конфет в 3 кучке до второго перекладывания. Следовательно, по окончании первого перекладывания:
в 3 — 6 конфет,
во 2-(8+ 6) конфет,
в 1—4 конфеты. Так как первый раз во вторую кучку переложили из первой 2 = 7 конфет, то первоначально в 1 кучке —11, во 2 кучке —7, в 3 — 6 конфет.
ЗАДАЧИ НА УСТАНОВЛЕНИЕ ЛОГИЧЕСКИХ СВЯЗЕЙ МЕЖДУ МНОЖЕСТВАМИ
Цель:1. Продемонстрировать три метода ответа:
— методом логических рассуждений
— табличный («логический квадрат»)
— посредством графов
2. В каждом методе продемонстрировать процесс установления связей при подлинном утверждении и при высказываний, отрицающих какие-либо факты.
3. Продемонстрировать использование способов при ответе других типов задач.
I МЕТОД-ПУТЕМ ЛОГИЧЕСКИХ РАССУЖДЕНИЙ
1. Саша и Федя носят фамилии Гвоздев и Шилов. Какую
фамилию носит любой, в случае, если Саша с Шиловым живут в сосед
них зданиях.
ОТВЕТ: В случае, если Саша с Шиловым живут в соседних зданиях, то Саша не Шилов, следовательно он Гвоздев, а Федя Шилов.
2. Три курицы за 3 дня снесли 3 яйца. какое количество яиц снесут
2 курицы за 6 дней?
ОТВЕТ: 3 курицы — 3 дня — 3 яйца
1 курица — 3 дня (!) — 1 яйцо
2 курицы — 3 дня — 2 яйца 2 курицы — 6 дней — 4 яйца
3. Три насоса за 3 часа выкачивают 3 тонны воды. какое количество тысячь киллограм воды выкачивают 12 насосов за 12 часов?
4. Два землекопа за 2 часа выкапывают 2 метра канавы. какое количество землекопов за 5 часов выкопают 5 метров канавы?
5. Аня и Маня имеют фамилии Строганова и Добрина. Какую фамилию имеет любая, в случае, если как мы знаем, что Маня и Добрина — одноклассницы.
II МЕТОД-ТАБЛИЧНЫЙ
|
6. Три подруги — Валя, Катя и Галя — пришли на сутки рождения в платьях различного цвета: розовом, голубом и желтом. Катя была не в желтом платье, Валя — не в желтом и не голубом. Кто из девочек пришел в каком платье.Нужно познакомить с правилами заполнения таблицы:
1. Подлинное утверждение отмечается знаком « + », фальшивое утверждение « — » (в логическом квадрате «х»).
2. В случае, если в строчке (столбике) имеется один « + », то остальные
« — ».
3. Заполняем таблицу по ходу чтения текста (отмечаем дан
ные связи), методом рассуждений дополняем и приобретаем ответ.
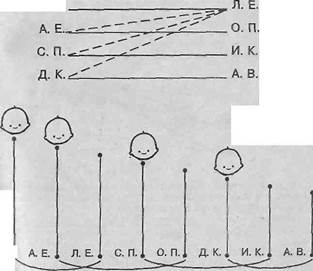
7. Четыре подруги пришли на каток, любая со своим братом. Они разбились на пары и начали кататься. Оказалось, что в каждой паре «кавалер» выше «женщины» и никто не катается со своей сестрой. Самый большой из компании — Юра Воробьев, следующий по росту — Андрей Егоров, позже Люся Егорова, Сережа Петров, Оля Петрова, Дима Крымов, Аня Воробьева и Инна Крымова. Кто с кем катался?
Люся Егорова может танцевать лишь с Юрой Воробьевым, т.к. Андрей Егоров ее брат, а Сережа и Дима ниже ее ростом. Рассуждая подобно, продолжи ответ.
8. Три клоуна Бим, Бом и Бам вышли на арену в красной, зеленой и синей рубахах. Их ботинки были тех же трех цветов. У Бима цвета туфель и рубашки совпадали. У Бома ни ботинки, ни рубаха не были красными. Бам был в зеленых туфлях, а в рубахе другого цвета. Как были одеты клоуны?
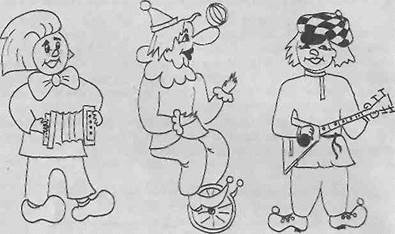
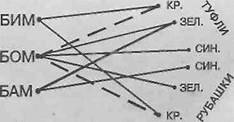
Бом возможно лишь в светло синий туфлях, тогда Бим в красных туфлях и в красной рубахе. Сейчас Бам возможно лишь в синей рубахе, тогда Бом в зеленой.
Итак:
| Имя Цвет | Туфель | Рубахи |
| Бим Бом Бам | Красный светло синий Зеленый | Красный Зеленый светло синий |
9. Встретились Белов, Рыжов и Чернов. Один из них был блондин, второй — брюнет, третий — рыжий. Брюнет сообщил Белову: «Ни у одного из нас цвет волос не соответствует фамилии». Какой цвет волос у каждого из них, в случае, если брюнеты в любой момент говорят правду? ОТВЕТ:
| Б. Ч.. Р. |
б бр р
| X | X | + |
| + | X | X |
| X | + | X |
10. Эдик, Миша и Вася заняли- первые. 4-места в соревнованиях, причем никакие два мальчика не дробили между собой место. На вопрос, какие конкретно они заняли места, мальчики честно
ответили: 1. Эдик — ни первое и ни третье; 2. Вася — второе; о. Андрей не был последним. Какие конкретно места заняли мальчики? Эдик имел возможность занять лишь 4 место, Андрей 1 либо 3, тогда Миша — 3 и 1.
Эдик . 1
Вася . 2
Андрей . 3
Миша . 4
Попытайся обозначить ответ сам.
11. Вилли, Билли и Дилли решили подарить Поночке на сутки рождения цветные шарики: желтого, синего цветов и красного, по цене 2 руб., 3 руб. и 5 рублей.
Вилли приобрел не красный и не светло синий, но самый дорогой шарик.
Билли — не красный и не недорогой.
Кто из братьев подарил какой шарик?
ЗАДАЧИ, РЕШАЕМЫЕ МЕТОДОМ СОСТАВЛЕНИЯ «ГРАФА» И ЛОГИЧЕСКИМ КВАДРАТОМ
1. В бутылке, стакане, кувшине,банке находятся молоко, лимонад, квас, вода. молоко и Вода не в бутылке, сосуд с лимонадом стоит между сосудом и кувшином с квасом, в банке не лимонад и не вода. Стакан стоит около сосуда с молоком. Куда налита любая жидкость?
2. Люба, Женя, юра и Саша взяли за контрольную работу отметки: 5, 5, 4, 3. Саша взял отметку больше, чем Люба, а Женя такую же, как Юра. Кто какую отметку взял?
3. Миша, Женя и Леня имеют фамилии Орлов, Ястребков и Соколов. Какую фамилию имеет любой из них, в случае, если. Женя Соколов и Миша — члены математического кружка, а Миша и Ястребков занимаются музыкой?
4. В шашечном турнире любой из ребят Миша, Серёжа и Яша — защищал честь собственного класса. Один из них получал образование
3 А, ВТОРОЙ в 3 Б, а третий — в 3 В. Первую партию игрались ученик и Миша 3 А класса. Вторую партию игрался Сережа с учеником 3 В класса, а Миша отдыхал. В каком классе обучается любой из ребят?
5. Петя, Саша и Ваня получают образование одной начальной школе, но в различных классах. Петя перешел в тот класс, в котором обучался Саша. Ване необходимо обучается еще один год, дабы перейти в тот класс, в котором обучается Петя. В каком классе обучается любой мальчик?
6. Три ученицы — Тополева, Березкина и Кленова — на пришкольном участке посадили три дерева: березку, тополь, клен.
— Весьма интересно оказалось, — что ни одна из вас не посадила дерево той породы, от которой случилась фамилия; определите, парни, какой породы деревце посадила Кленова, в случае, если это была не березка? А какие конкретно деревца посадили Тополева и Березкина?
7. Три подружки — Вера, Таня и Оля — пошли в лес по
ягоды. Для сбора ягод у них были корзинка, ведёрко и лукошко.
Как мы знаем, что Оля была не с корзинкой и не с лукошком, Вера не
с лукошком. Что забрала с собой любая девочка для сбора ягод?
Реши задачи способом исключения с применением таблиц (обозначим + и — все связи)
1. А, Б, В, Г — приятели. Один из них доктор, второй — журналист, третий — тренер спортивной школы, четвертый — инженер. Журналист написал статью об А и Г. журналист и Тренер вместе с Б ходили в поход. А и Б были на приеме у доктора. У кого какая профессия?
2. В — одном дворе живут 4 приятеля. шофер и Вадим старше Сергея. слесарь и Николай занимаются плаваньем, электрик — младший из друзей. По вечерам токарь и Антон играются в домино против электрика и Сергея. Выяснить профессию каждого.
3. На улице, поднявшись в кружок разговаривают, четыре девочки: Аня, Валя, Надя и Галя. Девочка в зеленом платье (не Валя и не Аня) стоит между девочкой в голубом платье и Надей. Девочка в белом платье стоит между девочкой в розовом платье и какое платье и Валей носит любая девочка?
4. В одном классе уроки по математике, истории и русскому языку вели три учителя: Архипов, Светлов и Морозов. Выясните кто из них какой предмет ведет, в случае, если как мы знаем, что:
а) все трое — Морозов, преподаватель Светлов и математики — идут из школы совместно к себе;
б) преподаватель истории старше учителя математики, а Морозов — самый младший среди них.
5. Кондратьев, Федоров и Давыдов живут на одной улице. Один из них трудится плотником, второй — маляром, третий — водопроводчиком. в один раз маляр пришел к плотнику, дабы попросить его починить дверь в собственной квартире, но ему заявили, что плотник оказывает помощь Федорову ремонтировать пол. Выясните профессию каждого, в случае, если как мы знаем, что водопроводчик ни при каких обстоятельствах не видел Давыдова.
6. Воронов, Павлов, Сахаров и Левицкий — четыре гениальных молодых человека. Один из них — танцор, второй — живописец, третий — певец, а четвертый — автор. Вот что о них известно:
а) художник и Воронов сидели в театре в тот вечер, в то время, когда
певец выступал в том месте с концертом;
б) писатель и Павлов совместно позировали живописцу;
в) автор написал биографическую повесть о собственном приятеле
Сахарове и планирует написать о втором приятеле, Воронове.
Назовите фамилии танцора, живописца, писателя и певца.
7. Поезд идет из Москвы в Минск. В поезде едут пассажиры
Иванов, Петров и Сидоров. В поездной бригаде такие же фами
лии у машиниста, кочегара и кондуктора. Как мы знаем, что:
а) пассажир Иванов живет в Москве, а пассажир Петров
живет в Минске. Однофамилец машиниста живет между Моск
вой и Минском.
б) Однофамилец кочегара приобретает ровно в три раза больше
кондуктора. Пассажир Петров приобретает в месяц 200 тыс. руб.
Выясните фамилии всех участников поездной бригады.
* 8. В купе одного из вагонов поезда едут 6 пассажиров, живущих в различных городах: Москве, С-Петербурге, Минске, Киеве, Одессе и Харькове. Их фамилии: Андреев, Борисов, Васильев, Григорьев, Елисеев и Дмитриев. При посадке Васильев помог жителю Одессы грузить багаж. В дороге стало известно, что москвич и Андреев — доктора, ленинградец и Дмитриев — преподавателя, минчанин и Васильев — инженеры, Елисеев и Борисов — участники Отечественной войны, а минчанин в армии не служил. харьковчанин и Андреев сошли в Киеве, а Васильев отправился дальше. Елисеев вел спор с ленинградцем о пользе нового лекарства. Выясните местожительство каждого из пассажиров и укажите их профессии.
* 9. Десять мальчиков: Александр, Борис, Василий, Георгий Дмитрий, Евгений, Захар, Иван, Леонид и Кирилл обучаются всё в различных классах десятилетней школы.
1) Старший брат Дмитрия оканчивает 7 класс, а младший
брат Евгения получает образование 5 классе. Александр старше Кирилла на один класс, а Леонид старше Евгения на два класса.
2) Василий не оканчивает школу в текущем году. Иван при окончании 4 класса взял грамоту. Борис — вожатый
в 5 классе, а Василий — в 4.
3) Александр, шестиклассник и Кирилл занимаются в гимнастической секции, а в один момент с ними тренируются баскетболисты, среди которых в любой момент Борис, Евгений и восьмиклассник.
4) семиклассник и Александр живут на улице Свободы, Георгий и пятиклассник на улице Пограничной, Дмитрий, восьмиклассник и первоклассник на Садовой, а десятиклассник и Кирилл — на Октябрьской.
5) Борис оказывает помощь в учебе Евгению, Дмитрий — Ивану, Георгий — Александру.
Кто из них в каком классе обучается?
* 10. На заводе трудились три приятеля: слесарь, токарь, сварщик. Их фамилии: Борисов, Иванов, Семенов. У слесаря нет ни братьев, ни сестер, он самый младший из друзей. Семенов женат на сестре Борисова, он старше токаря. Назови фамилии рабочих.
КОМБИНАТОРНЫЕ ЗАДАЧИ
Цели:1. Дать первые понятия перестановкам, размещениям, сочетаниям с повторением и без повторения.
2. Научить правилам полного перебора.
3. Научить решать задачи на разную комбинацию чисел.
Задачи для подготовки
В деревне Простоквашино на скамье перед домом сидят дядя Федор, кот Матроскин, пес Шарик, почтальон Печкин. В случае, если Шарик, сидящий крайним слева, сядет между Матроскиным и дядей Федором, то Федор окажется крайним слева. Кто где сидит?
Задачи на перестановку
1. Крокодил Гена решил позвонить Чебурашке по телефону, но внезапно понял, что забыл номер телефона. Гена отлично не забывает, что первые цифры 5 и 2. А остальные он не забывает, но забыл порядок. Это цифры: 1, 3, 4, 6. Какое самое много раз придется Гене собрать номер?
ОТВЕТ:
4-6
6 раз, в случае, если начать с цифры 1, аесли с вторых цифр, то 4 х 6 = 24 раза.
2. какое количество разных костюмов возможно составить из штанов и двух рубах, в случае, если костюм обязан складываться из штанов и одной рубахи?
3. От Бабы-Яги до Кащея ведет одна дорога, а от Кащея до Кикиморы — две дороги (см. рис.). какое количество методами возможно дойти от Бабы-Яги до Кикиморы, в случае, если нужно зайти к Кащею? Похожи ли задачи 2 и 3?
Кащей
| Баба-Яга |
Кикимора
4. От Марининого дома до Сашиного возможно проехать на велосипеде по двум дорогам (двумя методами), а от Сашиного дома до Лизиного — тремя методами (см. рис.). какое количество методами возможно доехать на велосипеде от Марины до Лизы, в случае, если по дороге нужно заехать к Саше?
5. Карлсон съел яблоко, персик и грушу. В каком порядке он м0г их съесть, в случае, если любой фрукт Карлсон ел раздельно? Перечисли все методы.
6. какое количество всего двузначных чисел возможно составить из цифр 1. 2. 3 при условии, что цифры в записи каждого числа не повторяются? Перечисли все эти числа и отыщи их сумму.
7. какое количество трехзначных чисел возможно составить из трех разных не равных нулю цифр? Зависит ли итог о того, какие конкретно конкретно цифры мы берем? Укажи какой-нибудь метод перебора трехзначных чисел, при котором ни одно число не может быть пропущено. Изменится ли число вариантов, в случае, если одна цифра — ноль?
8′. какое количество методами возможно переставить 3 разные буквы, 3 разные цифры, трех человек в последовательности, 3 книжки на полке? А какое количество методами возможно переставить 4 разных предмета? (А, В, С, Д).
9. какое количество дорог.
Из деревни Аленкино в деревню Борискино ведут 3 дороги. Из Борискина в Ваняткино — 4. А из Ваняткина в Галинкино — 5 дорог. какое количество методами возможно попасть в деревню Галинкино, шагая через Борискино и Ваняткино?
3-1=3 3-4=12 12 • 5 = 60 (способов)
10. Мамонтёнок в отыскивании мамы отправился в Африку. какое количество различными методами он может выбрать себе маршрут, плывя от островка к островку?
12. Белоснежка, Дюймовочка, Мальвина, Красная Золушка и Шапочка перед Новым годом решили поздравить по телефону ДРУГ друга с праздником. Причем, любая сказочная героиня переговорила по телефону с каждой из собственных подруг. какое количество всего было телефонных звонков?
Замечание: в случае, если Мальвина позвонила и поздравила Золушку, то будет ли Золушка звонить Мальвине?
13. В шахматном турнире приняли участие 7 человек. Любой с каждым сыграл по одной партии. какое количество партий они сыграли?
ОТВЕТ: 1 метод. Любой шахматист сыграл 6 партий. Всего сыграна 21 партия (произведение 7×6 необходимо поделить на два, в другом случае любая партия будет сосчитана два раза).
2 метод, (посредством графов). Пускай любой шахматист обозначен точкой, а любая сыгранная партия стрелкой от одного шахматиста к второму. (На рисунке обозначены партии лишь для первых двух игроков). В случае, если каждую партию вычислять один раз, то будем иметь 21 партию (6 + 5 + 4 + 3 + 2 + 1 = 21).
14. Семь человек обменялись фотографиями. какое количество наряду с этим было роздано фотографий?
Ответ. Т.к. любой из семи человек дал 6 фотографий (всем, не считая себя), то всего было роздано 42 фотографии