Разглядим процесс отражения плоской упругой волны на плоскостной границе двух (жидких либо газообразных) сред. Требуется взять аналитическое выражение для прохождения и коэффициентов отражения по колебательной скорости и давлению.
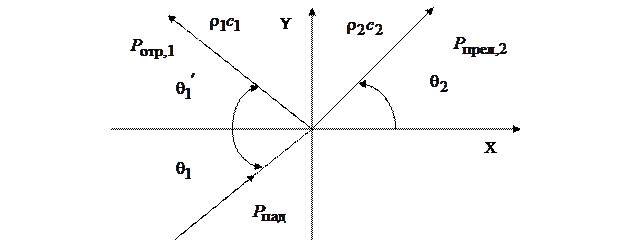
Рис. 3.5
Разглядим падение плоской волны в плоскости ХУ, в совокупности координат, представленной на рис. 3.5. Запишем аналитические выражения для всех волн, образующихся при наклонном падении:
,
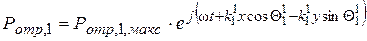 ,
, 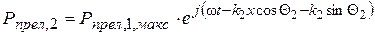 , (3.13)
, (3.13)
На плоской границе раздела должны быть выполнены граничные условия, характеризующие равновесие действующих сил и исполнение условий «сплошности» среды. Поле давления, действующего впервой среде: . Поле давления во второй среде: .
Граничное условие первого типа:
1. Равенство давлений по обе стороны границы
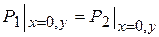 . (3.14)
. (3.14)
Граничное условие второго типа:
2. Равенство обычных компонент упругих колебательных скоростей и смещения, с учетом :
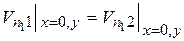 . (3.15)
. (3.15)
Для удобства вычислений безразмерных выражений введем дополнительные обозначения:
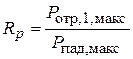 , (3.16)
, (3.16)
коэффициент отражения по давлению;
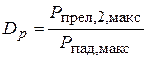 , (3.17)
, (3.17)
коэффициент прохождения по давлению.
Подставив полученные выражения для совокупности волн в граничные условия, возьмём совокупность двух уравнений с двумя малоизвестными R и D.
Ответ данной совокупности: при — «обычное» падение:
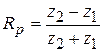 , (3.18)
, (3.18)
Наряду с этим было учтено, что по закону Снеллиуса:
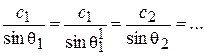 (3.20)
(3.20)
В случае, если в выражениях (3.18, 3.19) перейти к колебательным скоростям, то возможно взять выражения для прохождения и коэффициентов отражения по колебательной скорости:
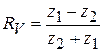 , (3.21)
, (3.21)
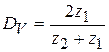 . (3.22)
. (3.22)
Видно, что эти выражения имеют различный темперамент, что подчеркивается различным физическим смыслом колебательной скорости и величин давления в звуковом поле. Выражения для прохождения и коэффициентов отражения по потенциалу подобны выражениям для коэффициентов по давлению. Выражения для коэффициентов отражения по упругим смещениям подобны выражениям прохождения и коэффициентов отражения по колебательной скорости.
Разглядим частные случаи соотношения импедансов прилегающих сред, от которых зависят значения, принимаемые выведенными коэффициентами:
1. полностью «мягкая» граница (вода – воздушное пространство):
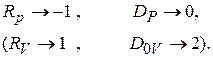 (3.23)
(3.23)
2. полностью «твёрдая» граница :
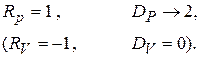 (3.24)
(3.24)
Выводы:
1.Отражающие особенности границы (проницаемость) зависят от различия импедансов «прилегающих» сред. При равенстве импедансов отражение отсутствует, и падающая волна абсолютно попадает во вторую среду.
2.Равенство импедансов предполагает конкретно равенство произведений плотностей сред на значения скоростей, а не равенство этих значений по отдельности.
3. прохождения и Коэффициенты отражения для различных физических размеров смогут для однообразных сочетаний сред принимать различные значения.
4. прохождения и Коэффициенты отражения для различных физических размеров не зависят от частоты.
Рассмотренные частные случаи практически определяют различия между двумя предельными состояниями «граничных» условий, обширно применяемых в «краевых» задачах математической физики:
Первое условие Дирихле, в противном случае именуемое условием на полностью «мягкой» либо «свободной» границе:
(3.25)
Второе условие Неймана, в противном случае именуемое условием на полностью «твёрдой» границе:
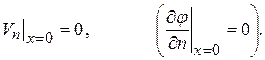 (3.26)
(3.26)
Практические следствия, формулируемые на основании найденных закономерностей, означают, в первую очередь, необходимость ответа задачи согласования импедансов, делаемую при построении солидного числа объектов живой и неживой природы. Помимо этого, при ответе так называемых обратных задач, в то время, когда пробуют восстанавливать профиль (соотношение импедансов) исследуемых сред по итогам ультразвуковых измерений, необходимо согласовывать число свободных измерений с числом восстанавливаемых параметров. Ясно, что по итогам измерений отраженного и прошедшего сигналов возможно вернуть два значения импедансов. Наряду с этим для конкретизации значения скорости либо плотности, непременно необходимы дополнительные измерения. Получение последних встречает затруднения, поскольку прохождения и коэффициенты отражения по отношению к плоской границе не зависят от частоты.
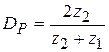 . (3
. (3