При рассмотрении схемы замещения цепи с распределенными параметрами были взяты дифференциальные уравнения в частных производных
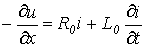 ; ; |
(5) |
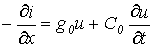
|
(6) |
Их интегрирование с учетом утрат представляет собой достаточно непростую задачу. В данной связи будем вычислять цепь линией без утрат, т.е. положим и . Такое допущение допустимо для линий с малыми утратами, и при анализе начальных стадий переходных процессов, довольно часто важнейших в отношении сверхтоков и перенапряжений.
С учетом указанного от соотношений (5) и (6) переходим к уравнениям
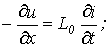
|
(7) |
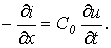
|
(8) |
Для получения уравнения (7) довольно одной переменной продифференцируем (7) по х, а (8) – по t:
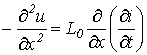 ; ; |
(9) |
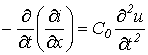 . . |
(10) |
Учитывая, что для линии без утрат 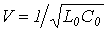 , по окончании подстановки соотношения (10) в (9) возьмём
, по окончании подстановки соотношения (10) в (9) возьмём
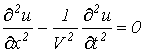 . . |
(11) |
Подобно получается уравнение для тока
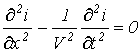 . . |
(12) |
Волновым уравнениям (11) и (12) удовлетворяют решения
;
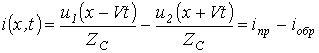 .
.
Как и ранее, прямые и тока и обратные волны напряжения связаны между собой законом Ома для волн
и ,
где 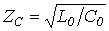 .
.
При расчете переходных процессов направляться не забывать:
- В любую секунду времени ток и напряжение в любой точке линии рассматриваются как следствие обратной волн и наложения прямой этих переменных на соответствующие размеры предшествующего режима.
- Всякое изменение режима работы цепи с распределенными параметрами обусловливает появление новых волн, накладываемых на существующий режим.
- Для каждой волны в отдельности выполняется закон Ома для волн.
Как указывалось, переходный процесс в цепях с распределенными параметрами характеризуется наложением многократно отраженных волн. Разглядим многократные отражения для двух самые характерных случаев: подключение источника постоянного напряжения к разомкнутой и короткозамкнутой линии.
Переходные процессы при включении на постоянное напряжение
разомкнутой и замкнутой на финише линии
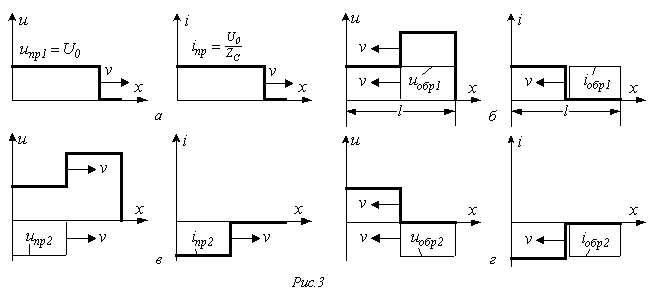
При замыкании рубильника (см. рис. 2) напряжение в начале линии сразу же достигает величины , и 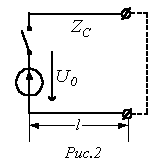 появляются прямые волны прямоугольной тока и формы напряжения , перемещающиеся на протяжении линии со скоростью V (см. рис. 3,а).Во всех точках линии, до которых волна еще не дошла, ток и напряжение равны нулю.Точка, ограничивающая участок линии, до которого дошла волна, именуется фронтом волны. В разглядываемом случае во всех точках линии, пройденных фронтом волны, напряжение равняется , а ток — .
появляются прямые волны прямоугольной тока и формы напряжения , перемещающиеся на протяжении линии со скоростью V (см. рис. 3,а).Во всех точках линии, до которых волна еще не дошла, ток и напряжение равны нулю.Точка, ограничивающая участок линии, до которого дошла волна, именуется фронтом волны. В разглядываемом случае во всех точках линии, пройденных фронтом волны, напряжение равняется , а ток — .
Напомним, что в настоящих условиях форма волны, зависящая от внутреннего сопротивления источника, параметров линии и т.п., в любой момент в большей либо меньшей степени отличается от прямоугольной.
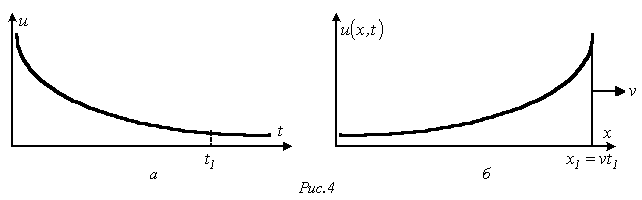
Помимо этого, при подключении к линии источника с другим законом трансформации напряжения форма волны будет другой. К примеру, при экспоненциальном характере трансформации напряжения источника (рис. 4,а) волна будет иметь форму на рис. 4,б.
В разглядываемом примере с прямоугольной волной напряжения при первом пробеге тока и волны напряжения (см. рис. 3,а) независимо от нагрузки имеют значения соответственно и , что связано с тем, что волны еще не дошли до конца линии, и, следовательно, условия в конце линии не смогут оказывать влияние на процесс.
В момент времени волны напряжения и тока доходят до конца линии длиной l, и нарушение однородности обусловливает появление обратных (отраженных) волн. Потому, что в конце линия разомкнута, то
,
откуда и .
В следствии (см. рис. 3,б) напряжение в линии, куда дошел фронт волны, удваивается, а ток спадает до нуля.
В момент времени , обратная волна напряжения, обусловливающая в линии напряжение , приходит к источнику, поддерживающему напряжение . В следствии появляется волна напряжения и соответствующая волне тока (см. рис. 3,в).
В момент времени волны напряжения и тока подойдут к концу линии. В связи с ХХ и (см. рис. 3,г). В то время, когда эти волны достигнут начала линии, ток и напряжение в ней окажутся равными нулю. Следовательно, с этого момента переходный процесс будет повторяться с периодичностью .
При короткозамкнутой на финише линии в промежутке времени картина процесса соответствует рассмотренной выше. При , потому, что в конце линии и , что приведет к возрастанию тока в линии за фронтом волны до величины . При от источника к концу линии будет двигаться волна напряжения и соответствующая ей волна тока , обусловливающая ток в линии, равный , и т. д. Так, при каждом пробеге волны ток в линии возрастает на .
Напомним, что в настоящем случае, т.е. при наличии утрат мощности, напряжение в линии в режиме ХХ понемногу выйдет на уровень, определяемый напряжением источника, а ток в режиме КЗ ограничится проводимостью линии и активным сопротивлением, и внутренним сопротивлением источника.
Литература
- Бессонов Л.А. Теоретические базы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных профессий институтов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретическиеосновы электротехники. Учеб. для институтов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.:Энергия- 1972. –200с.
- Базы теории цепей: Учеб. для институтов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
задачи и Контрольные вопросы
- Какой темперамент имеет зависимость входного сопротивления линии от ее длины и по какой причине?
- Посредством чего возможно изменять темперамент и величину входного сопротивления цепи с распределенными параметрами?
- Какое допущение лежит в базе анализа переходных процессов в долгих линиях?
- Каким законом связаны тока и волны напряжения в переходных режимах?
- Линия без утрат имеет длину , фазовая скорость волны . При каких частотах в ней будут иметь место максимумы и минимумы входного сопротивления?
Ответ: .
- При каких длинах линии без утрат в ней будут наблюдаться резонансные явления, в случае, если фазовая скорость равна скорости света, а частота ?
Ответ: .
- Выстройте тока распределения и эпюры напряжения на протяжении линии, питаемой от источника постоянного напряжения, при отключении и включении в ее финише резистивной нагрузки.
С учетом граничных условий расчет переходных процессов в цепях с распределенными параметрами возможно проводить как при нулевых, так и ненулевых начальных условиях. Но в первом случае анализ осуществляется в целом несложнее, что определяет целесообразность сведения расчета к нулевым начальным условиям. Пример для того чтобы сведения на базе принципа наложения для задачи на подключение в конце линии нагрузки схематично иллюстрирует рис. 1, где в последней схеме сопротивление имитирует входное сопротивление активного двухполюсника. 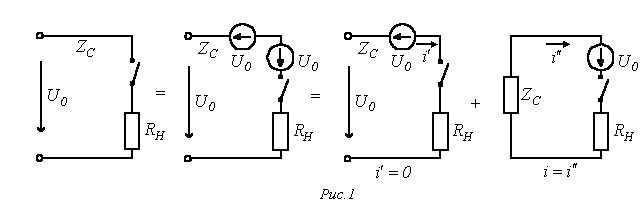 Так, в случае, если к линии, в общем случае заряженной, подключается некий в общем случае деятельный двухполюсник, то для нахождения появляющихся волн нужно выяснить напряжение на разомкнутых контактах ключа (рубильника), по окончании чего вычислить напряжения и токи в схеме с сосредоточенными параметрами, включаемой на это напряжение при нулевых начальных условиях. Полученные токи и напряжения накладываются на соответствующие размеры прошлого режима. При отключении нагрузки либо участков линии для расчета появляющихся тока и волн напряжения кроме этого возможно пользоваться способом сведения задачи к нулевым начальным условиям. В этом случае, зная ток в ветви с размыкаемым ключом (рубильником), нужно вычислить напряжения и токи в линии при подключении источника тока противоположного направления конкретно к финишам отключаемой ветви. После этого полученные напряжения и токи кроме этого накладываются на прошлый режим. Как пример для того чтобы расчета разглядим долгую линию без утрат на рис. 2, находящуюся под напряжением , к которой подключается дополнительный приемник с сопротивлением . 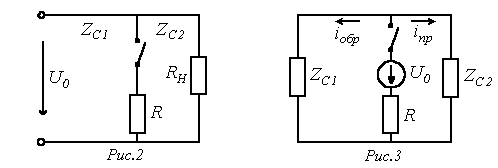 В соответствии со сформулированным выше правилом схема для расчета появляющихся при коммутации волн будет иметь вид на рис. 3. Тут 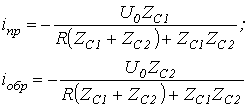 ; и в соответствии с законом Ома для волн ; и в соответствии с законом Ома для волн 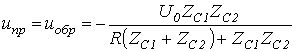 . Соответствующие взятым выражениям тока распределения и эпюры напряжения на протяжении линии представлены на рис. 4. . Соответствующие взятым выражениям тока распределения и эпюры напряжения на протяжении линии представлены на рис. 4. 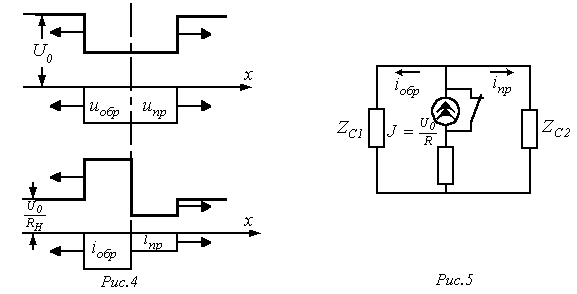 Напомним, что, потому, что 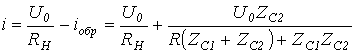 , к источнику от места подключения нагрузки отправилась волна, увеличивающая ток на этом месте. В случае, если напротив приемник с сопротивлением не подключается, а отключается, то расчет появляющихся наряду с этим напряжения и волн тока направляться осуществлять по схеме рис.5. Правило удвоения волны Пускай волна произвольной формы движется по линии с волновым сопротивлением и падает на некую нагрузку (см. рис. 6,а). , к источнику от места подключения нагрузки отправилась волна, увеличивающая ток на этом месте. В случае, если напротив приемник с сопротивлением не подключается, а отключается, то расчет появляющихся наряду с этим напряжения и волн тока направляться осуществлять по схеме рис.5. Правило удвоения волны Пускай волна произвольной формы движется по линии с волновым сопротивлением и падает на некую нагрузку (см. рис. 6,а). 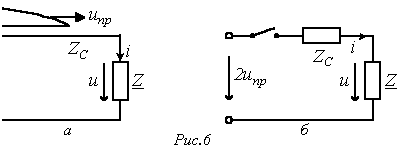 Для момента прихода волны к нагрузке возможно записать |
| ; | (1) |
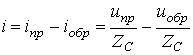
либо
| . | (2) |
Складывая (1) и (2), приобретаем
| . | (3) |
Соотношению (3) соответствует расчетная схема замещения с сосредоточенными параметрами, представленная на рис. 6,б. Момент замыкания ключа в данной схеме соответствует моменту падения волны на нагрузку в настоящей линии. Наряду с этим, потому, что цепь на рис. 6,б складывается из элементов с сосредоточенными параметрами, то расчет переходного процесса в ней возможно проводить любым из рассмотренных ранее способов (хорошим, операторным, с применением интеграла Дюамеля).
направляться подчернуть, что, в случае, если в долгой линии имеет место узел соединения вторых линий либо разветвление, то в соответствии с указанным подходом эту неоднородность направляться имитировать резистивным элементом с соответствующим сопротивлением, на что падает удвоенная волна.
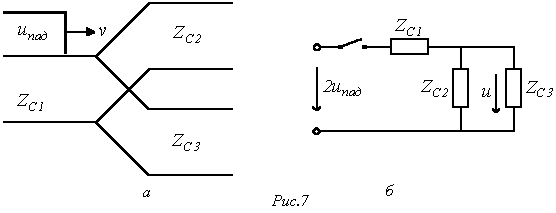
Пускай, к примеру, линия с волновым сопротивлением разветвляется на две параллельные линии с волновыми сопротивлениями и (см. рис. 7,а). Узел разветвления в расчетном замысле эквивалентен резистивному элементу с сопротивлением
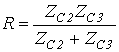 ,
,
наряду с этим расчетная схема замещения для момента прихода волны к стыку линий имеет форму на рис. 7,б.
Так, в случае, если падающая волна напряжения имеет величину и прямоугольную форму , то в соответствии со схемой замещения на рис. 7,б напряжение на стыке линий в момент прихода волны
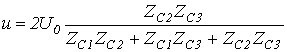 .
.
Данной величине будут равны волны напряжения, каковые отправятся потом в линии с волновыми сопротивлениями и . Отраженная же волна, которая отправится по линии с волновым сопротивлением , будет характеризоваться напряжением
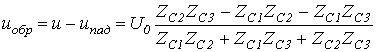 .
.
Так, по правилу удвоения волны определяются отраженные (показавшиеся в следствии отражения от неоднородности) и преломленные (прошедшие через неоднородность) волны, расчет которых осуществляется по схемам замещения с сосредоточенными параметрами. Следовательно, методика расчета переходных процессов в цепях с распределенными параметрами пребывает в последовательном составлении схем замещения с сосредоточенными параметрами для каждого момента прихода очередной падающей волны на очередную неоднородность и расчете по ним отраженных и преломленных волн.
Как пример разглядим падение прямоугольной волны напряжения величиной на включенный в конце линии конденсатор (см. рис. 8,а).
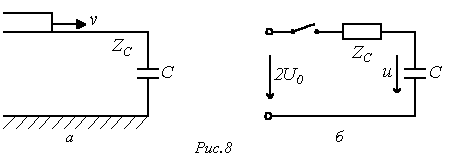
Для расчета напряжения на конденсаторе и тока через него в момент прихода волны к концу линии составим схему замещения с сосредоточенными параметрами (см. рис. 8,б). Для данной схемы возможно записать
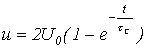 ,
,
где .
Это напряжение определяется суммой прямой (падающей) и обратной (отраженной) волн, т.е.
,
откуда для отраженной волны имеет место соотношение
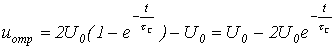
либо для той же волны в произвольной точке линии с координатой , отсчитываемой от финиша линии, с учетом запаздывания на время —
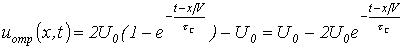 .
.
Соответственно для отраженной волны тока возможно записать
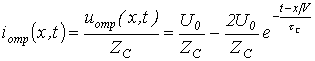 .
.
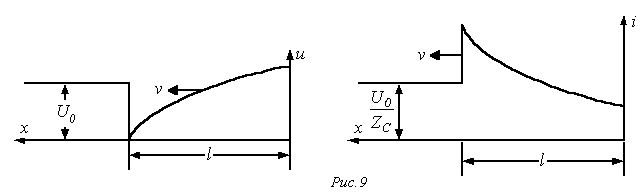
тока распределения и Эпюры напряжения на протяжении линии для момента времени , в то время, когда отраженная волна прошла некое расстояние , представлены на рис. 9. Сейчас напряжение на конденсаторе
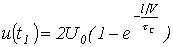
и ток через него
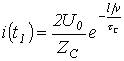 .
.
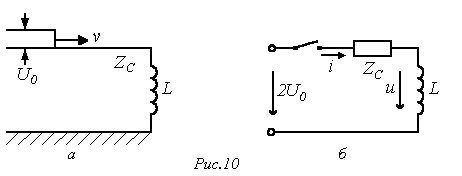
В качестве другого примера разглядим падение прямоугольной волны напряжения величиной на включенный в конце линии индуктивный элемент (см. рис. 10,а). В соответствии с расчетной схемой на рис. 10,б для тока через напряжения и катушку индуктивности на ней соответственно возможно записать
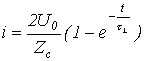 ;
;
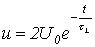 ,
,
где
С учетом этого выражения для тока и отражённых волн напряжения в произвольной точке линии имеют вид
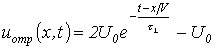 ;
;
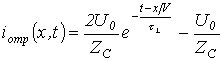 .
.
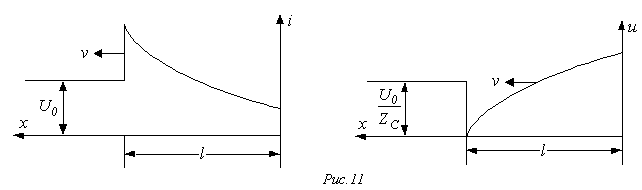
тока распределения и Эпюры напряжения на протяжении линии для момента времени приведены на рис. 11.
Литература
- Бессонов Л.А. Теоретические базы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных профессий институтов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретическиеосновы электротехники. Учеб. для институтов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.:Энергия- 1972. –200с.
- Базы теории цепей: Учеб. для институтов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
задачи и Контрольные вопросы
- Как расчет переходных процессов в долгих линиях сводится к нулевым начальным условиям?
- В чем суть правила удвоения волн, для чего оно употребляется?
- Сформулируйте методику расчета переходных процессов в цепях с распределенными параметрами.
- Что именуется отраженными и преломленными волнами?
- В линии на рис. 2 , , . Выяснить напряжения и волны тока, появляющиеся при коммутации, в случае, если .
Ответ: ; ; .
- Разглядеть падение волны напряжения, появившейся при коммутации в схеме прошлой задачи, на резистор и выяснить напряжения и обратные волны тока, образующиеся наряду с этим падении.
Ответ: ; .
- К линии, находящейся под напряжением , подключается
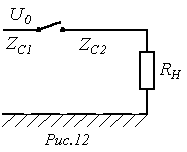 незаряженная линия (см. рис. 12). Выяснить напряжения и волны тока, появляющиеся при данной коммутации, в случае, если , .
незаряженная линия (см. рис. 12). Выяснить напряжения и волны тока, появляющиеся при данной коммутации, в случае, если , .
Ответ: ; ; .
- Разглядеть падение волны напряжения при коммутации в схеме прошлой задачи на резистор и выяснить появляющиеся наряду с этим тока и обратные волны напряжения.
Ответ: ; .
- Однородная долгая линия с нагружена на емкостный элемент с . Посередине линии параллельно ему включен еще один конденсатор с . От генератора на протяжении линии распространяется волна напряжения, которую до падения на конденсатор можно считать прямоугольной с . Записать выражение для напряжения на конденсаторе .
Ответ: 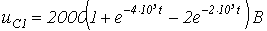 .
.