Определение скорости распространения
Звуковой волны в воздухе
Цель работы: познакомиться с способом определения звука посредством стоячей волны.
Литература
1. [ 1 ], §§ 7.8, 8.4.
2. [ 2 ], §§ 24, 25.
Вопросы входного контроля
1. Какие конкретно вопросы изучаются в разделе физики – «Акустика»?
2. Дать определение механической волны. Каковы ее главные характеристики?
3. Вывести уравнение бегущей волны.
4. Как распространяются механические волны в неоднородных средах?
5. Дать определение стоячей волны. Вывести уравнение стоячей волны и дать его анализ.
6. Как выяснить скорость звука способом стоячей волны?
1. Краткая теория
В совокупностях, в следствии сложения 2-х бегущих, распространяющихся навстречу друг другу, волн однообразной сдвига и частоты по фазе, появляется как следует новая волна – стоячая. В частности, в среде с ограниченным количеством это итог интерференции (сложения) волн падающей и отраженной.
1.1. Уравнение стоячей волны
Пускай в однородной полубесконечной среде в точке х=0 находится источник волны (И). Расстояние от источника до границы — . На границе раздела 2-х сред волна частично переходит в другую среду – преломляется, частично возвращается от границы (F) в первую — отражается (см. рис. 1).
 |
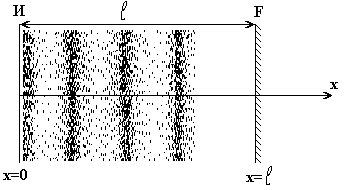Рис.1.
В каждой точке х волнового поля между точками х = 0 и х = будут складываться колебания, находящиеся в собствености 2-м идущим в различных направлениях волнам – бегущей и отраженной.
Смещение точки от положения равновесия в момент времени t в бегущей волне определяется уравнением:
, (1)
где с – скорость распространения волны в 1-ой среде,
А- амплитуда колебаний,
х – координаты точки.
Чтобы получить смещение от положения равновесия в момент t в отраженной волне (уравнение отраженной волны), нужно выяснить время запаздывания t возмущения от генератора до разглядываемой точки.
Потому, что отраженная волна прошла до границы расстояние l и от границы до точки с координатой х расстояние ( –х) для t имеем:
.
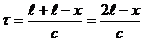Тогда S2 – смещение от положения равновесия в отраженной волне описывается законом:
(2)
В уравнение (2) учитывается быстрое изменение фазы волны на p при отражении. Результирующее смещение приобретаем, складывая уравнение (1) и (2):
.
Воспользовавшись тригонометрическим сложением косинусов
и формулами приведения имеем:
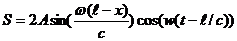. (3)
Уравнение (3) есть уравнением стоячей волны.
Анализ уравнения (3):
При сравнении (3) с уравнением гармонических колебаний:
, (4)
где А – амплитуда, постоянная величина,
— фаза колебаний,
— начальная фаза,
видно:
1. Выражение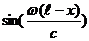 
есть амплитудой колебаний в точке с координатой х. По окончании его анализа возможно сделать вывод, что амплитуды точек в стоячей волне зависят от координат (в бегущей волне все амплитуды однообразны). Помимо этого, в таковой волне имеется точки, амплитуда которых велика (приобретаем из условия 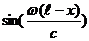=1). Эти точки именуются пучностями стоячей волны. Точки, в которых амплитуда минимальна (из условия 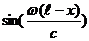= 0) именуются узлами стоячей волны.
2. Фаза колебаний определяется выражением:
.
Как видно, фаза колебаний не зависит от координаты х (в бегущей волне — координаты и функция, и времени).
Но потому, что выражение 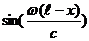меняет собственный символ при переходе через нуль (узел стоячей волны), все точки между 2-мя соседними узлами имеют смещение одного символа, а между следующими — другого.
3. Выражение играет роль начальной фазы.
В отличие от бегущей волны в стоячей волне нет переноса энергии (с этим связано наименование волны), т.к. обе волны несут навстречу друг другу в среднем однообразные энергии.
На рис.2 нарисовано пара последовательных положений результирующего смещения в стоячей волне в зависимости от координаты, соответствующих различным моментам времени t1,t2,t3.
 |
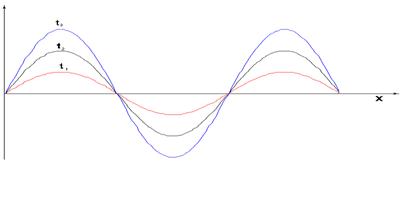S
Рис. 2.