Пускай m? N, — множество целых чисел. При делении каждого целого числа z? на m вероятны остатки 0, 1, 2, …, m-1, т.к. по теореме о делении с остатком z=mq+r, 0?r разбивается на классы. В любой класс входит лишь те целые числа, каковые при делении на m дают равные остатки. Обозначим классы следующим образом: , ,…, . При таком разбиении множества число m именуют модулем (обозначают mod m), а представитель каждого класса именуют вычетом.
Пример. m=4. При делении на 4 вероятны остатки 0, 1, 2, 3.
={-3, -4, 0, 4, 8, …}; ={-7, -3, 1, 5, 9, …};
={…,-6, -2, 2, 6, 10, …}; ={…,-1, 3, 7, …}.
Введя метод операции над классами следующим образом:
= = возможно продемонстрировать, что они владеют особенностями ассоциированности, дистрибутивности и коммутативности довольно . Приняв, помимо этого, класс за нейтральный элемент, а класс =( за противоположный, возможно продемонстрировать, что множество классов вычетов с выделенными операциями есть кольцом.
Определение 1.2. Два числа a и b именуются аналогичными по модулю m, если они являются вычетами одного и того же класса по модулю m.
Обозначают: .
Определение 1.3. Два числа a и b именуют аналогичными по модулю m, в случае, если при делении на m они дают равные остатки.
Теорема 1.4. Чтобы числа a и направляться были аналогичны по mod m нужно и достаточно, дабы их разность .
Подтверждение.
Необходимость.
? ? .
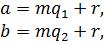Достаточность. Пускай , , то , либо + . Приобретаем равные остатки.
Свойства сравнений.
1 . Отношение есть отношением эквивалентности на множестве , т.е. оно владеет свойством рефлексивности, транзитивности и симметричности.
2 . Сравнения по одному и тому же модулю возможно почленно складывать, т.е. в случае, если и , то
.
Подтверждение.
По критерию имеем и . Тогда по свойствуотношения делимости , что и свидетельствует, что
.
Следствие1. К обеим частям сравнения возможно прибавить одно и также число.
Следствие2. К одной части сравнения в другую возможно переносить возможно переносить число с противоположным знаком.
3 . Сравнения по одному и тому же модулю возможно почленно перемножить, т.е. в случае, если и , то
.
Подтверждение.
Разглядим
Т.к. и , то по свойству отношения делимости , т.е. .
Следствие 1.Обе части сравнения возможно умножить на одно и также целое число.
Следствие 2. Обе части сравнения возможно возводить в одну и ту же натуральную степень.
4 . Обе части сравнения возможно поделить на одно да и то же число, взаимно простое с модулем, т.е. в случае, если и , то
.
Подтверждение.
По критерию имеем: , Т.к. , то по свойству взаимно несложных чисел т. е. .
5 Обе части сравнения и модуль возможно поделить на одно да и то же число, т.е. в случае, если , то .
Подтверждение.
По критерию имеем: , . Следовательно, , либо .
6 . В случае, если два числа аналогичны по некоему составному модулю, то они аналогичны по любому его делителю, т.е. в случае, если и , то .
Подтверждение.
По критерию имеем: и . Следовательно, по свойству отношения делимости .
7 .Обе части сравнения и модуль возможно умножить на одно и также натуральное число: в случае, если и , то .
Полная и приведенная совокупность вычетов.
Определение 1.4. В случае, если из каждого класса вычетов забрать по одному представителю, то система чисел именуется полной совокупностью вычетов.
Существуют самые употребительные полные совокупности вычетов: полная совокупность мельчайших неотрицательных, мельчайших по полной величине вычетов и мельчайших хороших вычетов.
Пример.
: {0, 1, 2, 3}- мельчайшие неотрицательные; {-1, 0, 1, 2}- мельчайшие по безотносительной величине; {1, 2, 3, 4}- мельчайшие хорошие.
Лемма 1.1. Совокупность чисел тогда и лишь тогда образует полную совокупность вычетов по модулю m, в то время, когда
1) числа попарно не аналогичны по модулю m;
2) количество чисел в совокупности равняется m.
Подтверждение.
Необходимость следует из определения.
Достаточность: Из 2) направляться, что каждое из чисел в собственности некоему классу вычетов по модулю m и каждые два числа принадлежат различным классам вычетов. Помимо этого, всего в совокупности m чисел, т.е. столько и должно быть в полной совокупности вычетов.
Определение 1.5. В случае, если из полной совокупности вычетов выбрать числа, взаимно простые с модулем m, то возьмём совокупность, которая именуется приведенной совокупностью вычетов.
Пример. и т.д.
По аналогии с леммой 1.1 легко проверить следующее утверждение.
Лемма 1.2. Совокупность чисел образует приведенную совокупность вычетов по модулю m тогда и лишь тогда, в то время, когда:
1) числа попарно не аналогичны по модулю m;
2) взаимно простые с модулем m;
3) количество чисел равняется , где — функция Эйлера.
Определение 1.6. Количество натуральных чисел, не превосходящих и взаимно несложных с именуется функцией Эйлера и обозначается .
Пример. =10. Взаимно простые с 10 числа 1, 3, 7, 9. Значит =4.
Замечание. Потому, что (1, 1)=1, полагают =1.
Разглядим задачу о вычислении значений функции Эйлера.
Теорема 1.5. В случае, если — простое число, — натуральное число, то .
Подтверждение.
Разглядим сперва случай . Ясно, что числа 1, 2, …, все взаимно простые с . Следовательно, = .
Пускай В последовательности чисел 1, 2, …, , , …, не взаимно несложными с являются только числа, простые с , т.е. каждое Всего таких чисел будет = . Так, .
Для того чтобы получить общую формулу для формулы Эйлера, докажем следующее ее ответственное свойство.
Теорема 1.6.Формула Эйлера мультипликативна, т.е. в случае, если , то .
Сейчас мы можем сформулировать неспециализированную теорему о вычислении значений Эйлера.
Теорема 1.7. Пускай — каноническое разложение числа . Тогда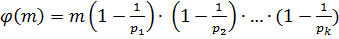 
.
Подтверждение.
Используя теорему 1.5 и 1.6, приобретаем: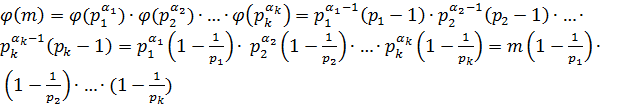 
.
Пример. 288= . Это значит, что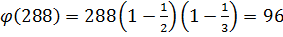 
.
Свойства полной и приведенной совокупности вычетов.
1 . Пускай . В случае, если и принимает все значения полной совокупности вычетов по модулю , , …, , то и принимает все значения полной совокупности вычетов по модулю , , …, .
Подтверждение.
Воспользуемся леммой 1.1:
1) Продемонстрируем, что при .
Предположим неприятное, что . Тогда . По свойству 4 сравнений тогда .Приобретаем несоответствие условию что принимает все значения полной совокупности вычетов. Следовательно, при .
2) Т.к. принимает значений, то также принимает значений.
По аналогии с прошлым свойством для полной совокупность вычетов возможно взять следующее утверждение.
2 . Пускай . В случае, если и принимает все значения приведенной совокупности вычетов по модулю , , …, , то и принимает все значения полной совокупности вычетов по модулю , , …, .
Теорема 1.8 Эйлера. В случае, если , то .
Подтверждение.
Пускай и принимает все значения приведенной совокупности вычетов , , …, по модулю . Тогда по свойству 2 кроме этого принимает все значения приведенной совокупности вычетов , , …, по тому же модулю . Исходя из этого и непременно будут сравнимы между собой по модулю , т.е. , , …,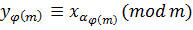 
.
По свойству 3 сравнений имеем , , …, , , …,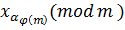 
. Т.к. , то по свойству взаимно несложных чисел , , …, . Следовательно, по свойству 4 уравнений, тогда имеем .
Следствие (Теорема Ферма): В случае, если p- легко число и , то либо .
Ответ сравнений.
Пускай дан многочлен , где .
Определение 1.7. Выражение вида (1.8) именуется сравнение с одним малоизвестным.
Решить сравнение — значит отыскать все такие целые числа , при которых сравнение справедливо. В качестве ответа сравнения мы будем разглядывать целый класс вычетов по модулю , любой представить которого удовлетворяет сравнению. Такие классы вычетов мы будем именовать корнями сравнения.
Как и при алгебраических уравнений, скажем, что два сравнения равносильны, в случае, если множества их корней однообразны.
Теорема 1.9. В случае, если в сравнении (1.8) коэффициенты , заменить числами, сравнимыми с ними по , то полученное сравнение будет равносильно исходному.
Следствие. В случае, если коэффициенты , делится на, то соответствующий член сравнения возможно удалить и взять равносильное сравнение.
Эти свойства смогут быть использованы для упрощения сравнений.
Пример. Сравнение равносильно сравнению .
Сравнения первой степени.
Сравнения первой степени мы будем записывать в виде
(*), где .
Исследуем вопрос о разрешимости сравнения (1.8) и нахождении его корней. Справедливо следующее утверждение.
Теорема 1.10. В случае, если , то сравнение (1.8) имеет единственное ответ.
Подтверждение.
Разглядим полную совокупность вычетов по модулю . Число в собственности одному и лишь одному из классов вычетов по модулю и, следовательно для него найдется одно и лишь одно число
, с которым оно находится в одном классе вычетов. Ясно, что соответствующие и порождает единственное ответ сравнения (1.8).
Теорема 1.11.В случае, если и , то сравнение (1.8) ответов не имеет.
Подтверждение.
В действительности, сравнение (1.8) возможно переписано в виде
, , либо , откуда, видно, что должно делиться на любой неспециализированный делитель и .
Теорема 1.12. В случае, если и , то уравнение (1.8) имеет ответов, каковые смогут быть отысканы по формуле:
где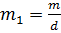 
и — единственное ответ сравнения
,(**)
где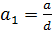 
, 
.
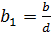Подтверждение.
Из сравнений 5 и 8 свойств направляться, что сравнения (*) и (**) равносильны.
В сравнении (**) имеем и исходя из этого, в силу теоремы 1.10, сравнение (**) имеет единственное ответ — некий класс вычетов по модулю . Это указывает, что числа вида
, , , …, (1.9)
удовлетворяют сравнениям (*), (**). Продолжать потом данный последовательность не имеет смысла, поскольку следующее число = и, значит, это число попадает в класс и т.д.
Все числа вида (1.9), по большому счету говоря, принадлежат различным классам вычетов по модулю . Вправду, по теореме 1.4 нужно, дабы разность делилась на модуль . Разглядим разность кратных участников: . Разумеется, она не делится на .
Методы ответа сравнений.
1) Метод опробований.
В большинстве случаев употребляется при маленьких значениях модуля. В этом случае выписывается вся полная совокупность вычетов и методом яркой подстановки (опробования) проверяется любой вычет.
Пример:
Так как , по теореме 1.10 сравнение имеет единственное ответ {0, 1, 2, 3, 4, 5, 6, 7,8}- полная совокупность мельчайших неотрицательных вычетов. , ,…, не делится на 9, .
Ответ: .
2) Метод преобразования правой части.
Данное сравнение заменяется равенством , и подбирается такое число , дабы правая часть делилась на коэффициент при .
Пример: ; . При t=2: 5 ; .
Ответ: .
3) Одним из самых действенных есть метод Эйлера.
По следствию 1 из свойства 3° сравнений имеем . Откуда по теореме 2.8 Эйлера .
Пример: ; .
, .
Ответ: .
4) Чтобы применить метод цепных дробей разложим дробь в цепную: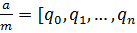 
]. Отыщем все подходящие дроби. По свойству 2° подходящих дробей тогда имеем либо .Из этого . В соответствии с следствию 1 из свойства 3° сравнений тогда имеем . Так, — ответ сравнения.
Пример: ;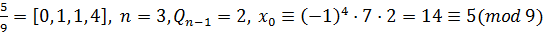 
.
Ответ: .
Использование сравнений первой степени к ответу неизвестных уравнений.
В начале пункта 1.2 мы узнали, что ответ неизвестного уравнения (1.5) сводится в нахождению какого-нибудь частного ответа при предположении, что .
Без ограничения общности будем вычислять Справедливо следующее утверждение.
Теорема 1.13. В случае, если -ответ уравнения (1.5), то — ответ уравнения . Обратно, в случае, если — ответ уравнения (!), то найдется -ответ уравнения (1.5).
Подтверждение.
Необходимость. Пускай -ответ уравнения (1.5), т.е. . Тогда , т.е. и следовательно, . Иначе, т.е. , и следовательно .
Достаточность. Пускай , тогда , что возможно записать как , т.е. .
Пример:
Ответ: